Płytki Ammann-Beenker - Ammann–Beenker tiling

Fragment płytek z aperiodycznego zestawu płytek A5 Ammanna, ozdobiony skończonymi, lokalnymi zasadami dopasowania, które wymuszają nieskończoną, globalną strukturę, taką jak płytki Amman-Beenker.

W geometrii , Dachówka Ammann-Beenker jest nonperiodic Dachówka , które mogą być generowane zarówno przez aperiodyczny zestaw prototiles jak zrobione przez Roberta Ammann w 1970, lub metodą cut-and-project jako wykonane niezależnie przez FPM Beenker . Ponieważ wszystkie dachówki otrzymane z płytek są nieokresowe, dachówki Ammanna-Beenkera są uważane za nieokresowe. Są jednym z pięciu zestawów dachówek odkrytych przez Ammanna i opisanych w Tilings and Patterns .

Dachówki Ammann-Beenker mają wiele właściwości podobnych do bardziej znanych dachówek Penrose :

• Są nieokresowe, co oznacza, że ​​brakuje im symetrii translacyjnej .
• Ich nieokresowość wynika z ich hierarchicznej struktury: nachylenia są nachyleniami zastępczymi wynikającymi z reguł zastępowania dla rosnących coraz większych łat. Ta struktura zastępowania oznacza również, że:
• Każdy skończony obszar (łata) w kafelku pojawia się nieskończenie wiele razy w tym kafelku i, w rzeczywistości, w każdym innym kafelku. Zatem wszystkie nieskończone nachylenia wyglądają do siebie podobnie, jeśli patrzy się tylko na skończone plamy.
• Są quasi -krystaliczne: zastosowane jako fizyczna struktura płytki Ammanna-Beenkera będą powodować dyfrakcję Bragga ; dyfraktogram ujawnia zarówno ośmiokrotną symetrię, jak i porządek dalekiego zasięgu. Porządek ten odzwierciedla fakt, że tendencje są organizowane nie poprzez symetrię translacyjną, ale raczej poprzez proces nazywany czasami „deflacją” lub „inflacją”.
• Cała ta nieskończona globalna struktura jest wymuszana przez lokalne zasady dopasowywania na parze płytek, jednym z najprostszych nieokresowych zestawów płytek, jakie kiedykolwiek znaleziono, zestaw Ammann A5.

Zaproponowano różne metody opisu dachów: zasady dopasowania, zastępstwa, schematy cięcia i projektu oraz pokrycia. W 1987 roku Wang, Chen i Kuo ogłosili odkrycie kwazikryształu o ośmiokątnej symetrii.

Opis płytek

Amman's A i B para płytek A5, ozdobione pasującymi zasadami; jakiekolwiek układanie płytek za pomocą tych płytek jest koniecznie nieokresowe, a zatem płytki są nieokresowe.

Zasady podstawienia Ammann A5, używane do udowodnienia, że ​​kafelki A5 mogą tworzyć tylko nieperiodyczne układy hierarchiczne, a zatem są kaflami aperiodycznymi.

Ta płytka istnieje w dwuwymiarowym rzucie ortogonalnym duopryzmatu 4D 8-8 zbudowanego z 16 ośmiokątnych pryzmatów .

Płytki A i B Ammana w jego parze A5 romb 45-135 stopni i trójkąt 45-45-90 stopni, ozdobione pasującymi regułami, które pozwalały tylko na pewne układy w każdym regionie, wymuszając struktury nieperiodyczne, hierarchiczne i kwaziperydyczne każdej z nieskończonej liczby pojedynczych oscylacji Ammanna-Beenkera.

Alternatywny zestaw płytek, również odkryty przez Ammanna i oznaczony jako „Ammann 4” w Grünbaum i Shephard, składa się z dwóch niewypukłych elementów o prostokątnych krawędziach. Jeden składa się z dwóch kwadratów nakładających się na mniejszy kwadrat, a drugi składa się z dużego kwadratu połączonego z mniejszym kwadratem. Poniższe diagramy przedstawiają kawałki i część dachówek.

To jest zasada zastępowania alternatywnego zestawu klocków.

Relacja między dwoma zestawami kafelków.

Oprócz strzałek na krawędziach w zwykłym zestawie klocków, zasady dopasowania dla obu zestawów klocków można wyrazić, rysując kawałki dużych strzał na wierzchołkach i wymagając, aby połączyły się w pełne strzałki.

Katz zbadał dodatkowe pochylenia dozwolone przez porzucenie ograniczeń wierzchołków i narzucenie tylko wymogu, aby strzałki krawędzi były zgodne. Ponieważ to wymaganie jest samo w sobie zachowane przez reguły podstawiania, każde nowe kafelkowanie ma nieskończoną sekwencję „powiększonych” kopii uzyskanych przez kolejne zastosowania reguły podstawiania. Każdy kafelek w sekwencji jest nie do odróżnienia od prawdziwego kafelka Ammanna-Beenkera w coraz większej skali. Ponieważ niektóre z tych płytek są okresowe, wynika z tego, że żadna dekoracja płytek, która wymusza aperiodyczność, nie może być określona przez spojrzenie na jakąkolwiek skończoną plamę płytki. Orientację strzałek wierzchołków, które wymuszają aperiodyczność, można zatem wydedukować tylko z całej nieskończonej płytki.

Kafelkowanie ma również ekstremalną właściwość: wśród dachówek, których romb naprzemiennie występują naprzemiennie (to znaczy, gdy dwa romby sąsiadują ze sobą lub są oddzielone rzędem kwadratów, pojawiają się w różnych orientacjach), stwierdza się, że udział kwadratów jest minimalny w –Tilings Beenker.

Cechy proporcji śrutu i srebra

Płytki Ammanna-Beenkera są ściśle związane ze stosunkiem srebra ( ) i liczbami Pella . ${\ displaystyle 1 + {\ sqrt {2}}}$

• podstawienie schemat przedstawia stosunek jako współczynnik skalowania: jego macierzy jest macierz podstawień Pella, a szereg słów wytwarzane przez podstawienie mają tę właściwość, że liczba s i s są równe kolejnych numerach Pella. ${\ Displaystyle R \ do RrR; r \ do R}$${\ displaystyle r}$${\ displaystyle R}$
• te wartości własnych macierzy podstawień i . ${\ displaystyle 1 + {\ sqrt {2}}}$${\ displaystyle 1 - {\ sqrt {2}}}$
• W alternatywnym zestawie płytek długie krawędzie mają razy dłuższe boki niż krótkie. ${\ displaystyle 1 + {\ sqrt {2}}}$
• Jeden zestaw robaków Conway , utworzony przez krótkie i długie przekątne rombów, tworzy powyższe struny, z r jako krótką przekątną i R jako długą przekątną. Dlatego też pręty Ammann tworzą również kratki zamówione przez firmę Pell.

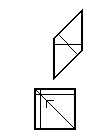Ammann bary dla zwykłych klocków. Jeśli pogrubione linie zewnętrzne mają długość , paski podzielą krawędzie na odcinki długości i . ${\ displaystyle 2 {\ sqrt {2}}}$${\ displaystyle 1 + {\ sqrt {2}}}$${\ displaystyle {\ sqrt {2}} - 1}$

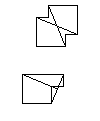Pręty Ammann dla alternatywnego zestawu klocków. Zwróć uwagę, że pręty asymetrycznej płytki częściowo wystają poza nią.

Konstrukcja typu cut-and-project

Tesseractic plastra miodu ma symetrię obrotową ośmiokrotnie, odpowiadające ośmiokrotnie symetrii obrotowej tesserakt . Macierz rotacji reprezentująca tę symetrię to:

${\ Displaystyle A = {\ rozpocząć {bmatrix} 0 i 0 i 0 i -1 \\ 1 i 0 i 0 i 0 \\ 0 i -1 i 0 i 0 \\ 0 i 0 i -1 i 0 \ koniec {bmatrix}}.}$

Przekształcenie tej macierzy na nowe współrzędne podane przez

${\ displaystyle B = {\ początek {bmatrix} -1 / 2 i 0 i -1 / 2 i {\ sqrt {2}} / 2 \\ 1/2 i {\ sqrt {2}} / 2 i -1 / 2 i 0 \\ - 1 / 2 & 0 & -1 / 2 & - {\ sqrt {2}} / 2 \\ - 1/2 & {\ sqrt {2}} / 2 & 1/2 & 0 \ end {bmatrix}}}$ będzie produkować:

${\ displaystyle BAB ^ {- 1} = {\ początek {bmatrix} {\ sqrt {2}} / 2 & {\ sqrt {2}} / 2 i 0 i 0 \\ - {\ sqrt {2}} / 2 i {\ sqrt { 2}} / 2 & 0 & 0 \\ 0 & 0 & - {\ sqrt {2}} / 2 & {\ sqrt {2}} / 2 \\ 0 & 0 & - {\ sqrt {2}} / 2 & - {\ sqrt {2}} / 2 \ end {bmatrix}}.}$

Ta trzecia macierz odpowiada wówczas obrotowi zarówno o 45 ° (w dwóch pierwszych wymiarach), jak i o 135 ° (w dwóch ostatnich). Następnie możemy uzyskać kafelek Ammanna-Beenkera, rzutując blok hipersześcianek wzdłuż pierwszych dwóch lub dwóch ostatnich współrzędnych.

Alternatywnie, kafelek Ammanna-Beenkera można uzyskać, rysując romb i kwadraty wokół punktów przecięcia pary kwadratowych kratownic o równej skali nałożonych pod kątem 45 stopni. Te dwie techniki zostały opracowane przez Beenkera w jego artykule.

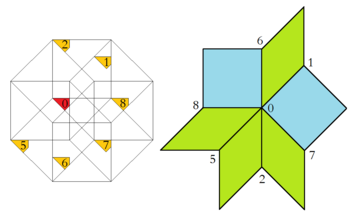
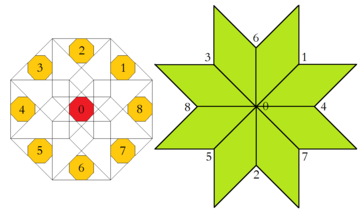
Powiązanym, wielowymiarowym osadzeniem w tesseraktycznym plastrze miodu jest konstrukcja Klotza, jak opisano szczegółowo w jej zastosowaniu tutaj w artykule Baake i Joseph. W ten sposób ośmiokątna domena akceptacji może być dalej podzielona na części, z których każda daje początek dokładnie jednej konfiguracji wierzchołków. Co więcej, względna powierzchnia każdego z tych obszarów jest równa częstotliwości odpowiadającej konfiguracji wierzchołków w nieskończonym kafelkowaniu.

Region domeny akceptacji i odpowiednia konfiguracja wierzchołków

Odniesienia i uwagi

Linki zewnętrzne

• Wpis w Encyklopedii Tilings .
• Płytki Ammann-Beenker na stronie internetowej Johna Savarda .
• Pokazuje linie Ammanna dla kafelkowania i zasady zastępowania .