Powierzchnia - Area
| Powierzchnia | |
|---|---|
Wspólne symbole |
A |
| Jednostka SI | metr kwadratowy [m 2 ] |
| W jednostkach podstawowych SI | 1 m 2 |
| Wymiar | |
Powierzchnia to wielkość wyrażająca zasięg dwuwymiarowego regionu , kształtu lub płaskiej blaszki , w płaszczyźnie . Powierzchnia jest jego analog w dwuwymiarowej powierzchni z trójwymiarowego obiektu . Powierzchnia może być rozumiana jako ilość materiału o danej grubości jaka byłaby potrzebna do ukształtowania modelu kształtu lub ilość farby potrzebna do pokrycia powierzchni jednorazową warstwą. Jest to dwuwymiarowa analog długości z krzywej (jednowymiarowy koncepcji) lub objętości stałego (koncepcji trójwymiarowej).
Obszar kształtu można zmierzyć, porównując kształt do kwadratów o ustalonym rozmiarze. W Międzynarodowym Układzie Miar (SI) standardową jednostką pola jest metr kwadratowy (zapisany jako m 2 ), czyli pole kwadratu o boku jednego metra . Kształt o powierzchni trzech metrów kwadratowych miałby taką samą powierzchnię jak trzy takie kwadraty. W matematyce The kwadratowe urządzenie jest zdefiniowany tak, że jeden obszar, a obszar o innym kształcie lub powierzchni, jest wielkością bezwymiarową liczbą rzeczywistą .

Istnieje kilka dobrze znanych wzorów dla obszarów o prostych kształtach, takich jak trójkąty , prostokąty i koła . Korzystając z tych wzorów, pole dowolnego wielokąta można znaleźć, dzieląc wielokąt na trójkąty . W przypadku kształtów z zakrzywioną granicą do obliczenia powierzchni zwykle wymagany jest rachunek różniczkowy . Istotnie, problem wyznaczania pola powierzchni figur płaskich był główną motywacją historycznego rozwoju rachunku różniczkowego .
W przypadku kształtu bryłowego, takiego jak kula , stożek lub walec, obszar jego powierzchni granicznej jest nazywany polem powierzchni . Wzory na pola powierzchni prostych kształtów zostały obliczone przez starożytnych Greków , ale obliczenie pola powierzchni bardziej skomplikowanego kształtu zwykle wymaga rachunku różniczkowego wielu zmiennych .
Obszar odgrywa ważną rolę we współczesnej matematyce. Oprócz oczywistego znaczenia w geometrii i rachunku różniczkowym, obszar ten jest związany z definicją wyznaczników w algebrze liniowej i jest podstawową właściwością powierzchni w geometrii różniczkowej . W analizie powierzchnia podzbioru płaszczyzny jest określana za pomocą miary Lebesgue'a , choć nie każdy podzbiór jest mierzalny. Ogólnie rzecz biorąc, obszar w wyższej matematyce jest postrzegany jako szczególny przypadek objętości dla regionów dwuwymiarowych.
Obszar można określić za pomocą aksjomatów, definiując go jako funkcję zbioru pewnych figur płaskich do zbioru liczb rzeczywistych. Można udowodnić, że taka funkcja istnieje.
Formalna definicja
Podejście do zdefiniowania tego, co rozumie się przez „obszar”, opiera się na aksjomatach . „Powierzchnia” może być zdefiniowana jako funkcja ze zbioru M specjalnych rodzajów figur płaskich (zwanych zbiorami mierzalnymi) do zbioru liczb rzeczywistych, która spełnia następujące własności:
- Dla wszystkich S w M , a ( S ) ≥ 0.
- Jeśli S i T są w M , to także S ∪ T i S ∩ T , a także a ( S ∪ T ) = a ( S ) + a ( T ) − a ( S ∩ T ).
- Jeśli S i T są w M z S ⊆ T wtedy T − S jest w M i a ( T − S ) = a ( T ) − a ( S ).
- Jeśli zbiór S jest w M, a S jest przystający do T, to T również jest w M i a ( S ) = a ( T ).
- Każdy prostokąt R jest w M . Jeśli prostokąt ma długość h i szerokość k to a ( R ) = hk .
- Niech Q będzie zbiorem zawartym pomiędzy dwoma regionami schodkowymi S i T . Region schodkowy jest utworzony ze skończonej sumy sąsiednich prostokątów spoczywających na wspólnej podstawie, tj. S ⊆ Q ⊆ T . Jeżeli istnieje unikatowa liczba c taka, że a ( S ) ≤ c ≤ a ( T ) dla wszystkich takich regionów stopni S i T , wtedy a ( Q ) = c .
Można wykazać, że taka funkcja obszaru faktycznie istnieje.
Jednostki

Każdej jednostce długości odpowiada jednostka powierzchni, czyli pole kwadratu o danej długości boku. W ten sposób obszary mogą być mierzone w metrach kwadratowych (m 2 ) centymetrów kwadratowych (cm 2 ), milimetrach kwadratowych (mm 2 ), kilometrów kwadratowych (km 2 ) stóp kwadratowych (ft 2 ) jardów kwadratowych (m 2 ) mil kwadratowych (mi 2 ) i tak dalej. Algebraicznie jednostki te można traktować jako kwadraty odpowiednich jednostek długości.
Jednostką powierzchni SI jest metr kwadratowy, który jest uważany za jednostkę pochodną SI .
Konwersje
Obliczenie powierzchni kwadratu o długości i szerokości 1 metra wynosiłoby:
1 metr × 1 metr = 1 m 2
i tak prostokąt o różnych bokach (powiedzmy długość 3 metry i szerokość 2 metry) miałby powierzchnię w jednostkach kwadratowych, którą można obliczyć jako:
3 metry × 2 metry = 6 m 2 . Odpowiada to 6 milionom milimetrów kwadratowych. Inne przydatne konwersje to:
- 1 kilometr kwadratowy = 1 000 000 metrów kwadratowych
- 1 metr kwadratowy = 10 000 centymetrów kwadratowych = 1 000 000 milimetrów kwadratowych
- 1 centymetr kwadratowy = 100 milimetrów kwadratowych.
Jednostki niemetryczne
W jednostkach niemetrycznych konwersja między dwiema jednostkami kwadratowymi jest kwadratem konwersji między odpowiednimi jednostkami długości.
stosunek między stopami kwadratowymi a calami kwadratowymi wynosi
- 1 stopa kwadratowa = 144 cale kwadratowe,
gdzie 144 = 12 2 = 12 × 12. Podobnie:
- 1 jard kwadratowy = 9 stóp kwadratowych
- 1 mila kwadratowa = 3 097 600 jardów kwadratowych = 27 878 400 stóp kwadratowych
Ponadto współczynniki konwersji obejmują:
- 1 cal kwadratowy = 6,4516 centymetrów kwadratowych
- 1 stopa kwadratowa = 0,092 903 04 metrów kwadratowych
- 1 jard kwadratowy = 0,836 127 36 metrów kwadratowych
- 1 mila kwadratowa = 2,589 988 110 336 kilometrów kwadratowych
Inne jednostki, w tym historyczne
Istnieje kilka innych wspólnych jednostek dla obszaru. Are była pierwotna jednostka powierzchni w systemie metrycznym , z:
- 1 are = 100 metrów kwadratowych
Chociaż areał wyszedł z użycia, hektar nadal jest powszechnie używany do pomiaru gruntów:
- 1 hektar = 100 arów = 10 000 metrów kwadratowych = 0,01 kilometra kwadratowego
Inne rzadkie jednostki metryczne w dziedzinie obejmują tetradê Z hectad , a mnóstwo .
Akr jest również powszechnie stosowane do pomiaru obszarów lądowych, gdzie
- 1 akr = 4840 jardów kwadratowych = 43560 stóp kwadratowych.
Akr to około 40% hektara.
W skali atomowej powierzchnia jest mierzona w jednostkach oborów , tak że:
- 1 stodoła = 10–28 metrów kwadratowych.
Stodoła jest powszechnie używana do opisu pola przekroju w fizyce jądrowej .
W Indiach ,
- 20 durek = 1 dur
- 20 dur = 1 khatha
- 20 khata = 1 bigha
- 32 khata = 1 akr
Historia
Obszar okręgu
W 5 wieku pne Hipokrates z Chios był pierwszym, aby pokazać, że obszar dysku (region otoczone okręgu) jest proporcjonalna do kwadratu jego średnicy, jako część jego kwadraturze z Księżyce Hipokratesa , ale nie nie identyfikować stałej proporcjonalności . Eudoksos z Knidos , również w V wieku pne, również odkrył, że powierzchnia dysku jest proporcjonalna do kwadratu jego promienia.
Następnie, Book I Euklidesa Elementy rozpatrywane równości pomiędzy obszarami figur dwuwymiarowych. Matematyk Archimedes użył narzędzi geometrii euklidesowej, aby pokazać, że obszar wewnątrz koła jest równy trójkątowi prostokątnemu, którego podstawa ma długość obwodu koła i którego wysokość jest równa promieniowi koła, w swojej książce Pomiar koła . (Obwód wynosi 2 π r , a pole trójkąta to połowa podstawy razy wysokość, co daje pole π r 2 dla dysku.) Archimedes przybliżył wartość π (a więc pole koła o jednostkowym promieniu ) swoją metodą podwojenia , w której wpisał w okrąg trójkąt foremny i zanotował jego powierzchnię, następnie podwoił liczbę boków, aby uzyskać sześciokąt foremny , a następnie wielokrotnie podwoił liczbę boków w miarę zbliżania się powierzchni wielokąta do tego okręgu (i zrobił to samo z opisanymi wielokątami ).
Szwajcarski naukowiec Johann Heinrich Lambert w 1761 roku udowodnił, że π , stosunek powierzchni koła do jego kwadratu, jest niewymierny , co oznacza, że nie jest równy ilorazowi dowolnych dwóch liczb całkowitych. W 1794 francuski matematyk Adrien-Marie Legendre udowodnił, że π 2 jest irracjonalne; dowodzi to również, że π jest irracjonalne. W 1882 roku niemiecki matematyk Ferdinand von Lindemann udowodnił, że π jest transcendentalne (nie jest rozwiązaniem żadnego równania wielomianowego ze współczynnikami wymiernymi), potwierdzając przypuszczenie zarówno Legendre'a, jak i Eulera.
Obszar trójkąta
Czapla (lub Bohater) z Aleksandrii znalazł tak zwany wzór Herona na pole trójkąta pod względem jego boków, a dowód można znaleźć w jego książce Metrica , napisanej około 60 roku n.e. Sugerowano, że Archimedes znał formułę ponad dwa wieki wcześniej, a ponieważ Metryka jest zbiorem wiedzy matematycznej dostępnej w starożytnym świecie, możliwe jest, że formuła ta poprzedza odniesienie podane w tej pracy.
W 499 Aryabhata , wielki matematyk - astronom z klasycznej epoki indyjskiej matematyki i indyjskiej astronomii , określił powierzchnię trójkąta jako połowę podstawy razy wysokość Aryabhatiya (rozdział 2.6).
Formuła równoważna Heron została odkryta przez Chińczyków niezależnie od Greków. Został opublikowany w 1247 w Shushu Jiuzhang (" Traktat matematyczny w dziewięciu sekcjach "), napisanym przez Qin Jiushao .
Obszar czworoboku
W VII wieku n.e. Brahmagupta opracował formułę, obecnie znaną jako formuła Brahmagupty, określającą powierzchnię czworoboku cyklicznego ( czworokąta wpisanego w okrąg) pod względem jego boków. W 1842 roku niemieccy matematycy Carl Anton Bretschneider i Karl Georg Christian von Staudt niezależnie odnaleźli formułę, znaną jako formuła Bretschneidera , na pole dowolnego czworoboku.
Ogólny obszar wielokąta
Opracowanie współrzędnych kartezjańskich przez René Descartesa w XVII wieku umożliwiło opracowanie przez Gaussa w XIX wieku wzoru geodezyjnego dla obszaru dowolnego wielokąta o znanych położeniach wierzchołków .
Obszary wyznaczone za pomocą rachunku różniczkowego
Rozwój rachunku całkowego pod koniec XVII wieku dostarczył narzędzi, które można później wykorzystać do obliczania bardziej skomplikowanych obszarów, takich jak pole elipsy i pole powierzchni różnych zakrzywionych obiektów trójwymiarowych.
Formuły powierzchni
Wzory wielokątów
Dla wielokąta nie przecinającego się ( prostego ) o współrzędnych kartezjańskich ( i =0, 1, ..., n -1) którego n wierzchołków jest znanych, pole powierzchni jest określone wzorem mierniczego :
gdzie gdy i = n -1, to i +1 jest wyrażone jako moduł n, a więc odnosi się do 0.
Prostokąty
Najbardziej podstawową formułą pola jest formuła pola prostokąta . Mając prostokąt o długości l i szerokości w , wzór na pole to:
- A = lw (prostokąt).
Oznacza to, że powierzchnia prostokąta to długość pomnożona przez szerokość. W szczególnym przypadku, gdy l = w w przypadku kwadratu, pole kwadratu o długości boku s jest określone wzorem:
- A = s 2 (kwadrat).
Wzór na pole prostokąta wynika wprost z podstawowych własności pola i bywa przyjmowany jako definicja lub aksjomat . Z drugiej strony, jeśli geometria jest rozwijany przed arytmetyczny , wzór ten może być używany do określenia mnożenie z liczb rzeczywistych .
Rozcięcie, równoległoboki i trójkąty
Większość innych prostych wzorów na pole powierzchni wynika z metody sekcji . Wiąże się to z pocięciem kształtu na kawałki, których obszary muszą sumować się z obszarem pierwotnego kształtu.
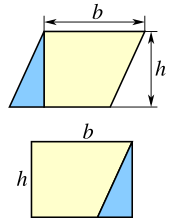
Na przykład dowolny równoległobok można podzielić na trapez i trójkąt prawy , jak pokazano na rysunku po lewej stronie. Jeśli trójkąt zostanie przesunięty na drugą stronę trapezu, wynikowa figura jest prostokątem. Wynika z tego, że pole równoległoboku jest takie samo jak pole prostokąta:
- A = bh (równoległobok).
Jednak ten sam równoległobok można również przeciąć po przekątnej na dwa przystające trójkąty, jak pokazano na rysunku po prawej stronie. Wynika z tego, że pole każdego trójkąta to połowa pola równoległoboku:
- (trójkąt).
Podobne argumenty można wykorzystać do znalezienia wzorów pola dla trapezu, jak i bardziej skomplikowanych wielokątów .
Obszar zakrzywionych kształtów
Kręgi
Wzór na pole koła (bardziej poprawnie nazywany polem zamkniętym przez okrąg lub polem dysku ) opiera się na podobnej metodzie. Mając okrąg o promieniu r , można podzielić okrąg na sektory , jak pokazano na rysunku po prawej stronie. Każdy sektor ma kształt w przybliżeniu trójkątny, a sektory można przestawić, aby utworzyć przybliżony równoległobok. Wysokość tego równoległoboku wynosi r , a szerokość to połowa obwodu koła, czyli π r . Zatem całkowita powierzchnia koła wynosi π r 2 :
- A = π r 2 (koło).
Chociaż rozcięcie użyte w tym wzorze jest tylko przybliżone, błąd staje się coraz mniejszy, gdy okrąg jest dzielony na coraz więcej sektorów. Granica pól przybliżonych równoległoboków to dokładnie π r 2 , czyli pole koła.
Ten argument jest w rzeczywistości prostym zastosowaniem idei rachunku różniczkowego . W starożytności w podobny sposób wyznaczano pole koła metodą wyczerpania , która obecnie jest uznawana za prekursora rachunku całkowego . Stosując nowoczesne metody, pole koła można obliczyć za pomocą całki oznaczonej :
Elipsy
Wzór na obszar zamknięty elipsą jest powiązany z wzorem koła; dla elipsy o półmałych i półmałych osiach x i y wzór jest następujący:
Powierzchnia

Większość podstawowych wzorów na pole powierzchni można uzyskać, wycinając powierzchnie i spłaszczając je. Na przykład, jeśli boczna powierzchnia walca (lub dowolnego pryzmatu ) jest przecięta wzdłużnie, można ją spłaszczyć do prostokąta. Podobnie, jeśli cięcie zostanie wykonane wzdłuż boku stożka , powierzchnia boczna może zostać spłaszczona w wycinek koła, a wynikowy obszar zostanie obliczony.
Wzór na pole powierzchni kuli jest trudniejszy do wyprowadzenia: ponieważ kula ma niezerową krzywiznę Gaussa , nie można jej spłaszczyć. Wzór na pole powierzchni kuli został po raz pierwszy otrzymany przez Archimedesa w swojej pracy O sferze i cylindrze . Formuła to:
- A = 4 πr 2 (sfera),
gdzie r jest promieniem kuli. Podobnie jak w przypadku wzoru na pole koła, każde wyprowadzenie tego wzoru z natury wykorzystuje metody podobne do rachunku różniczkowego .
Ogólne wzory
Obszary figur dwuwymiarowych
- Trójkąt : (gdzie B oznacza dowolny z boku, a H jest odległością od linii, w którym B leży na drugim wierzchołku trójkąta). Ten wzór można zastosować, jeśli znana jest wysokość h . Jeśli znane są długości trzech boków, to można zastosować wzór Herona : gdzie a , b , c są bokami trójkąta i stanowią połowę jego obwodu. Jeżeli kąt a jego dwa boki zawarte są dane, jest obszar , w którym C jest podany kąt a i b są zawarte jego boków. Jeśli trójkąt jest wykreślony na płaszczyźnie współrzędnych, można zastosować macierz i jest ona uproszczona do wartości bezwzględnej . Ten wzór jest również znany jako wzór na sznurowadła i jest łatwym sposobem obliczenia pola trójkąta współrzędnych, zastępując 3 punkty (x 1 ,y 1 ) , (x 2 ,y 2 ) i (x 3 ,y 3 ) . Wzór na sznurowadło można również wykorzystać do znalezienia obszarów innych wielokątów, gdy znane są ich wierzchołki. Innym podejściem do trójkąta współrzędnych jest użycie rachunku różniczkowego do znalezienia obszaru.
- Wielokąt prosty zbudowany na siatce o równej oddalone punktów (czyli punktów z całkowitych współrzędnych), tak, że wszystkie wierzchołki wielokąta są punkty siatki: gdzie i oznacza liczbę punktów siatki wewnątrz wielokąta i b oznacza liczbę punktów granicznych . Ten wynik jest znany jako twierdzenie Picka .
Obszar w rachunku różniczkowym
- Obszar między krzywą o wartości dodatniej a osią poziomą, mierzony między dwiema wartościami a i b (b jest zdefiniowany jako większa z dwóch wartości) na osi poziomej, jest określony przez całkę od a do b funkcji, która przedstawia krzywą:
- Obszar pomiędzy wykresami dwóch funkcji jest równa do całki jednej funkcji , f ( x ), minus całki drugiej funkcji g ( x ):
- gdzie jest krzywa z większą wartością y.
- Obszar ograniczony funkcją wyrażoną we współrzędnych biegunowych to:
- Obszar zamknięty krzywą parametryczną z punktami końcowymi jest określony przez całki krzywoliniowe :
- lub z -component od
- (Szczegóły patrz twierdzenie Greena § Obliczanie powierzchni .) Jest to zasada działania urządzenia mechanicznego planimetru .
Obszar ograniczony między dwiema funkcjami kwadratowymi
Aby znaleźć obszar ograniczony między dwiema funkcjami kwadratowymi , odejmujemy jedną od drugiej, aby zapisać różnicę jako
gdzie f ( x ) jest kwadratową granicą górną, a g ( x ) jest kwadratową granicą dolną. Określić wyróżnik z F ( x ) - g ( x ) w postaci
Upraszczając wzór na całkę między wykresami dwóch funkcji (jak podano w punkcie powyżej) i korzystając ze wzoru Viety , możemy uzyskać
Powyższe pozostaje ważne, jeśli jedna z funkcji ograniczających jest liniowa, a nie kwadratowa.
Pole powierzchni figur trójwymiarowych
- Stożek : , gdzie r jest promieniem podstawy kołowej, a h jest wysokością. Można to również przepisać jako lub gdzie r jest promieniem, a l jest skośną wysokością stożka. to powierzchnia podstawowa, a powierzchnia boczna stożka.
- cube : , gdzie s jest długością krawędzi.
- cylinder : , gdzie r jest promieniem podstawy, a h jest wysokością. 2 R mogą być również zapisane jako d , gdzie d jest średnicą.
- graniastosłup : 2B + Ph, gdzie B to powierzchnia podstawy, P to obwód podstawy, a h to wysokość graniastosłupa.
- ostrosłup : , gdzie B to powierzchnia podstawy, P to obwód podstawy, a L to długość skosu.
- prostopadłościan : , gdzie to długość, w to szerokość, a h to wysokość.
Ogólny wzór na pole powierzchni
Ogólny wzór na pole powierzchni wykresu funkcji ciągle różniczkowalnej gdzie i jest obszarem w płaszczyźnie xy o gładkiej granicy:
Jeszcze bardziej ogólny wzór na pole powierzchni wykresu powierzchni parametrycznej w postaci wektorowej, gdzie jest ciągle różniczkowalną funkcją wektorową, to:
Lista formuł
| Kształt | Formuła | Zmienne |
|---|---|---|
| Prostokąt |

|
|
| Trójkąt |

|
|
| Trójkąt |

|
|
|
Trójkąt ( Wzór Czapli ) |

|
|
| Trójkąt równoramienny |

|
|
| Regularny trójkąt |

|
|
| Romb / Latawiec |

|
|
| Równoległobok |

|
|
| trapez |

|
|
| Sześciokąt regularny |

|
|
| Regularny ośmiokąt |

|
|
|
Wielokąt foremny ( boki) |
|
( obwód ) incircle promień circumcircle promień
|
| Koło |
( średnica ) |

|
| Sektor o obiegu zamkniętym |

|
|
| Elipsa |

|
|
| Całka |

|
|
| Powierzchnia | ||
|
Kula |

|
|
| Prostopadłościan |

|
|
|
cylinder (w tym dół i góra) |

|
|
|
Stożek (wraz z dołem) |

|
|
| Torus |

|
|
| Powierzchnia rewolucji |
(obrót wokół osi x) |

|
Powyższe obliczenia pokazują, jak znaleźć obszary o wielu wspólnych kształtach .
Obszary nieregularnych (a więc dowolnych) wielokątów można obliczyć za pomocą „ Wzoru geodezyjnego ” (wzór sznurowadła).
Stosunek powierzchni do obwodu
Nierówność izoperymetryczna wskazuje, że do zamkniętej krzywej o długości L (tak, że otacza obszar ma obwód L ) oraz do obszaru A w regionie, w którym zamyka on,
a równość obowiązuje wtedy i tylko wtedy, gdy krzywa jest kołem . Okrąg ma więc największą powierzchnię ze wszystkich zamkniętych figur o danym obwodzie.
Z drugiej strony, figura o danym obwodzie L może mieć dowolnie małą powierzchnię, co ilustruje romb, który jest „przechylony” dowolnie daleko, tak że dwa z jej kątów są dowolnie bliskie 0°, a pozostałe dwa są dowolnie blisko do 180°.
W przypadku koła stosunek pola powierzchni do obwodu (wyrażenie określające obwód koła) jest równy połowie promienia r . Widać to ze wzoru pola πr 2 i wzoru obwodu 2 πr .
Powierzchnia wielokąta foremnego to połowa jego obwodu razy apotem (gdzie apotem jest odległością od środka do najbliższego punktu z dowolnej strony).
Fraktale
Podwojenie długości krawędzi wielokąta mnoży jego powierzchnię przez cztery, czyli dwa (stosunek długości nowego do starego boku) podniesione do potęgi dwójki (wymiar przestrzeni, w której znajduje się wielokąt). Ale jeśli jednowymiarowe długości fraktala narysowanego w dwóch wymiarach są podwojone, przestrzenna zawartość skal fraktalnych o potęgę dwójki niekoniecznie jest liczbą całkowitą. Ta moc nazywana jest fraktalnym wymiarem fraktala.
Dwusieczne obszaru
Istnieje nieskończona liczba linii, które przecinają obszar trójkąta na pół. Trzy z nich są mediany trójkąta (które łączą punkty przecięcia boków o wierzchołkach przeciwległych) i są one zbieżne w tego trójkąta ciężkości ; w rzeczywistości są to jedyne dwusieczne obszaru, które przechodzą przez środek ciężkości. Każdy wiersz poprzez trójkąta, który dzieli obszar zarówno trójkąt i jego obwód w połowie przechodzi incenter trójkąta (w środku jego incircle ). W każdym trójkącie jest jeden, dwa lub trzy z nich.
Każda linia przechodząca przez środek równoległoboku przecina obszar na pół.
Wszystkie dwusieczne obszaru okręgu lub innej elipsy przechodzą przez środek, a wszelkie akordy przechodzące przez środek przecinają obszar na pół. W przypadku koła są to średnice koła.
Optymalizacja
Biorąc pod uwagę kontur drutu, powierzchnia najmniej rozpiętej powierzchni („wypełnienie”) jest powierzchnią minimalną . Znane przykłady to bańki mydlane .
Kwestia obszaru napełniania z riemannowskiej kręgu pozostaje otwarta.
Okrąg ma największą powierzchnię ze wszystkich dwuwymiarowych obiektów o tym samym obwodzie.
Cykliczny wielokąt (jeden wpisany okrąg) ma największą powierzchnię dowolnego wielokąta z danej liczby stron tych samych długościach.
Wersja nierówności izoperymetrycznej dla trójkątów mówi, że trójkąt o największej powierzchni spośród wszystkich o danym obwodzie jest równoboczny .
Trójkąt największego pola wszystkich wpisanych w dany okrąg jest równoboczny; a trójkąt o najmniejszym polu ze wszystkich opisanych wokół danego okręgu jest równoboczny.
Stosunek powierzchni okręgu do powierzchni trójkąta równobocznego , jest większy niż w przypadku dowolnego trójkąta nierównobocznego.
Stosunek powierzchni do kwadratu obwodu trójkąta równobocznego jest większy niż w przypadku każdego innego trójkąta.
Zobacz też
- Czworokąt Brahmagupta , cykliczny czworokąt z bokami całkowitymi, przekątnymi całkowitymi i obszarem całkowitym.
- Mapa równikowa
- Trójkąt heronowy , trójkąt z bokami całkowitymi i powierzchnią całkowitą.
- Lista nierówności trójkątów
- Trójkąt o jednej siódmej powierzchni , trójkąt wewnętrzny z jedną siódmą powierzchni trójkąta odniesienia.
- Twierdzenie Routha , uogólnienie trójkąta o powierzchni jednej siódmej.
- Rzędy wielkości — lista obszarów według wielkości.
- Wyprowadzenie formuły pięciokąta
- Planimeter , przyrząd do pomiaru małych powierzchni, np. na mapach.
- Powierzchnia wypukłego czworoboku
- Pięciokąt Robbinsa , cykliczny pięciokąt, którego długość boków i powierzchnia są liczbami wymiernymi.






















































































![{\ Displaystyle A = 2 \ pi \ int _ {a} ^ {b} \! f (x) {\ sqrt {1 + \ lewo [f' (x) \ po prawej] ^ {2}}} \ operatorname { d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07cf6da325a77c650339de80d9b00d984ca3751d)


