Podstawa (algebra liniowa) - Basis (linear algebra)

Ten sam wektor można przedstawić w dwóch różnych podstawach (fioletowe i czerwone strzałki).

W matematyce , A zestaw B z wektorów w przestrzeni wektor V jest nazywana podstawą , gdy każdy element V mogą być zapisywane w sposób szczególny, jako skończonej kombinacji liniowej elementów B . Współczynniki tej kombinacji liniowej są określane jako składowe lub współrzędne wektora względem B . Elementy podstawy nazywane są wektory bazowe .

Równoważnie zbiór B jest bazą, jeśli jego elementy są liniowo niezależne i każdy element V jest kombinacją liniową elementów B . Innymi słowy, baza jest liniowo niezależnym zbiorem rozpinającym .

Przestrzeń wektorowa może mieć kilka baz; jednak wszystkie bazy mają taką samą liczbę elementów, zwaną wymiarem przestrzeni wektorowej.

Ten artykuł zajmuje się głównie skończenie wymiarowymi przestrzeniami wektorowymi. Jednak wiele zasad obowiązuje również dla nieskończenie wymiarowych przestrzeni wektorowych.

Definicja

Podstawy B z przestrzeni wektorowej V nad polu F (na przykład z liczb rzeczywistych R lub liczbami zespolonymi C ) jest liniowo niezależne podzbiór o V że przęsła V . Oznacza to, że podzbiór B zbioru V jest podstawą, jeśli spełnia dwa następujące warunki:

• właściwość liniowej niezależności :

  dla każdego skończonego podzespołu z B jeśli dla niektórych z F , a następnie ; oraz${\ Displaystyle \ {\ mathbf {v} _ {1} \ dotsc \ mathbf {v} _ {m} \}}$${\ Displaystyle c_ {1} \ mathbf {v} _ {1} + \ cdots + c_ {m} \ mathbf {v} _ {m} = \ mathbf {0}}$${\displaystyle c_{1},\kropki,c_{m}}$${\ Displaystyle c_ {1} = \ cdots = c_ {m} = 0}$

• obejmujących nieruchomości:

  dla każdego wektora v w V , można wybrać w F i w B taki, że .${\displaystyle a_{1},\dotsc,a_{n}}$${\ Displaystyle \ mathbf {v} _ {1}, \ kropki, \ mathbf {v} _ {n}}$${\ Displaystyle \ mathbf {v} = a_ {1} \ mathbf {v} _ {1} + \ cdots + a_ {n} \ mathbf {v} _ {n}}$

W skalary nazywane są współrzędne wektora v w stosunku do podstawy B , a przez pierwsze własności są jednoznacznie określone. ${\displaystyle a_{i}}$

Przestrzeń wektorowa, która ma skończoną bazę, nazywa się skończenie-wymiarową . W takim przypadku skończony podzbiór może być traktowany jako sam B , aby sprawdzić liniową niezależność w powyższej definicji.

Często wygodne lub nawet konieczne jest uporządkowanie na podstawie wektorów bazowych, na przykład przy omawianiu orientacji lub gdy rozważa się współczynniki skalarne wektora względem bazy bez wyraźnego odniesienia się do elementów bazowych. W tym przypadku kolejność jest konieczna do powiązania każdego współczynnika z odpowiednim elementem bazowym. To uporządkowanie można wykonać, numerując podstawowe elementy. W celu podkreślenia, że rozkaz został wybrany, mówi się o uporządkowanej podstawie , która nie jest ona po prostu niestrukturalnych zestaw , ale sekwencja An indeksowaną Family , lub tym podobne; patrz § Zamówione bazy i współrzędne poniżej.

Przykłady

Ten rysunek ilustruje standardową podstawę w R ² . Wektory niebieski i pomarańczowy to elementy podstawy; zielony wektor może być podany w postaci wektorów bazowych, a więc jest od nich liniowo zależny .

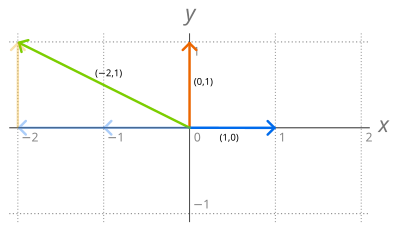
• Zestaw R ² z uporządkowanych par z liczb rzeczywistych jest przestrzeń wektorową o następujących właściwościach:

  dodawanie składników

  ${\ Displaystyle (a, b) + (c, d) = (a + c, b + d),}$

  i mnożenie przez skalar

  ${\ Displaystyle \ lambda (a, b) = (\ lambda a \ lambda b)}$

  gdzie jest dowolna liczba rzeczywista. Prosta baza tej przestrzeni wektorowej, zwana bazą standardową, składa się z dwóch wektorów e ₁ = (1,0) i e ₂ = (0,1) , ponieważ każdy wektor v = ( a , b ) z R ² może być jednoznacznie napisane jako ${\ Displaystyle \ lambda}$

  ${\ Displaystyle \ mathbf {v} = a \ mathbf {e} _ {1} + b \ mathbf {e} _ {2}}.$

  Każda inna para liniowo niezależnych wektorów R ² , takich jak (1, 1) i (-1, 2) , również stanowi bazę R ² .

• Mówiąc ogólnie, jeśli M jest pole , zestaw z n -tuples elementów F jest przestrzeń wektorową o zdefiniowana dodawania i mnożenia skalarnego. Pozwolić ${\ Displaystyle F ^ {n}}$

  ${\ Displaystyle \ mathbf {e} _ {i} = (0, \ ldots, 0,1,0, \ ldots, 0)}$

  jest n -tuple wszystkie komponenty są równe 0, z wyjątkiem ı TH, która jest 1. Następnie stanowi podstawę , która jest nazywana

  standardową podstawę z${\ Displaystyle \ mathbf {e} _ {1} \ ldots \ mathbf {e} _ {n}}$${\ Displaystyle F ^ {n},}$${\ Displaystyle F ^ {n}.}$
• Jeśli C jest w pole, wielomian pierścień F [ X ] z wielomianów jednym zawierane na czas nieokreślony jest F -wektor przestrzeni i ma podstawę B , zwany Jednomian podstawy , składający się z wszystkich jednomianów :

  ${\ Displaystyle B = \ {1, X, X ^ {2}, \ ldots \}.}$

  Podstawą jest również dowolny zbiór wielomianów taki, że istnieje dokładnie jeden wielomian każdego stopnia. Taki zbiór wielomianów nazywamy ciągiem wielomianowym . Przykładami (wśród wielu) takich wielomianów są wielomiany bazowe Bernsteina i wielomiany Czebyszewa .

Nieruchomości

Wiele własności baz skończonych wynika z lematu wymiany Steinitza , który mówi, że dla dowolnej przestrzeni wektorowej V , mając skończony zbiór rozpinający S i zbiór liniowo niezależny L składający się z n elementów V , można zastąpić n dobrze dobranymi elementami S przez elementy L, aby uzyskać zbiór opinający zawierający L , mający inne elementy w S i mający taką samą liczbę elementów jak S .

Większość własności wynikających z lematu wymiany Steinitza pozostaje prawdziwa, gdy nie ma zbioru skończonego, ale ich dowody w przypadku nieskończonym na ogół wymagają aksjomatu wyboru lub jego słabszej formy, takiej jak lemat ultrafiltracji .

Jeśli V jest przestrzenią wektorową nad ciałem F , to:

• Jeżeli L jest liniowo niezależnym podzbiorem zbioru rozpinającego S ⊆ V , to istnieje baza B taka, że

  ${\ Displaystyle L \ podzbiór B \ podzbiór S.}$

• V ma podstawę (jest to poprzednia właściwość, w której L jest zbiorem pustym , a S = V ).
• Wszystkie podstawy V mają taką samą liczność , która nazywa się wymiar z V . To jest twierdzenie o wymiarze .
• Prądotwórczego S stanowi podstawę V , wtedy i tylko wtedy, gdy jest minimalny, a więc nie podzbiorem z S jest zbiorem generowania V .
• Zbiór liniowo niezależny L jest bazą wtedy i tylko wtedy, gdy jest maksymalny, to znaczy nie jest podzbiorem właściwym żadnego zbioru liniowo niezależnego.

Jeżeli V jest przestrzenią wektorową o wymiarze n , to:

• Podzbiór V składający się z n elementów jest podstawą wtedy i tylko wtedy, gdy jest liniowo niezależny.
• Podzbiór V składający się z n elementów jest podstawą wtedy i tylko wtedy, gdy obejmuje zbiór V .

Współrzędne

Niech V będzie przestrzenią wektorową o skończonym wymiarze n nad ciałem F , oraz

${\ Displaystyle B = \ {\ mathbf {b} _ {1} \ ldots \ mathbf {b} _ {n} \}}$

być podstawą V . Z definicji podstawy, każde v w V można zapisać w unikalny sposób jako

${\ Displaystyle \ mathbf {v} = \ lambda _ {1} \ mathbf {b} _ {1} + \ cdots + \ lambda _ {n} \ mathbf {b} _ {n}}$

gdzie współczynniki są skalarne (czyli elementy F ), które nazywane są współrzędne z V na B . Jednakże, jeśli mówimy o zestawie współczynników, traci się zgodność między współczynnikami a elementami bazowymi i kilka wektorów może mieć ten sam zestaw współczynników. Na przykład i mają ten sam zestaw współczynników {2, 3} i są różne. Dlatego często wygodnie jest pracować na uporządkowanej podstawie ; zwykle robi się to poprzez indeksowanie elementów bazowych według pierwszych liczb naturalnych. Wówczas współrzędne wektora tworzą ciąg podobnie indeksowany, a wektor jest całkowicie scharakteryzowany przez ciąg współrzędnych. Uporządkowana podstawa nazywana jest również ramką , słowem powszechnie używanym w różnych kontekstach, odnoszącym się do ciągu danych, pozwalającym określić współrzędne. ${\ Displaystyle \ lambda _ {1} \ ldots \ lambda _ {n}}$${\ Displaystyle 3 \ mathbf {b} _ {1} +2 \ mathbf {b} _ {2}}$${\ Displaystyle 2 \ mathbf {b} _ {1} + 3 \ mathbf {b} _ {2}}$

Niech, jak zwykle, będzie zbiorem n -krotek elementów F . Zbiór ten jest przestrzenią F -wektorową, z dodawaniem i mnożeniem przez skalar zdefiniowanymi komponentowo. Mapa ${\ Displaystyle F ^ {n}}$

${\ Displaystyle \ varphi: (\ lambda _ {1} \ ldots \ lambda _ {n}) \ mapsto \ lambda _ {1} \ mathbf {b} _ {1} + \ cdots + \ lambda _ {n }\mathbf {b} _{n}}$

jest izomorfizmem liniowym z przestrzeni wektorowej na V . Innymi słowy, jest to układzie współrzędnych z V i n -tuple jest wektor współrzędnych z v . ${\ Displaystyle F ^ {n}}$${\ Displaystyle F ^ {n}}$${\ Displaystyle \ varphi ^ {-1} (\ mathbf {v})}$

Odwrotny obraz o o to n -tuple której wszystkie składniki są 0, z wyjątkiem tego , że p, który jest 1. Forma uporządkowaną podstawą , która jest wywoływana jego standardową podstawę albo podstawę kanonicznej . Uporządkowana podstawa B jest obrazem podstawy kanonicznej .${\displaystyle \varphi}$${\ Displaystyle \ mathbf {b} _ {i}}$${\ Displaystyle \ mathbf {e} _ {i}}$${\ Displaystyle \ mathbf {e} _ {i}}$${\ Displaystyle F ^ {n}}$${\displaystyle \varphi}$${\ Displaystyle F ^ {n}}$

Z powyższego wynika, że ​​każda uporządkowana baza jest obrazem przez izomorfizm liniowy bazy kanonicznej , a każdy izomorfizm liniowy od na V można zdefiniować jako izomorfizm odwzorowujący bazę kanoniczną na daną bazę uporządkowaną V . Innymi słowy jest to równoważne zdefiniowaniu uporządkowanej bazy V , czyli liniowego izomorfizmu z na V . ${\ Displaystyle F ^ {n}}$${\ Displaystyle F ^ {n}}$${\ Displaystyle F ^ {n}}$${\ Displaystyle F ^ {n}}$

Zmiana podstawy

Niech V będzie przestrzenią wektorową wymiaru n nad ciałem F . Biorąc pod uwagę dwie (zamówione) podstawy i na V , to często jest użyteczne do ekspresji współrzędnych wektora x w odniesieniu do poziomu w odniesieniu do współrzędnych względem Może to być wykonane przez wzorze przełączenia z bazowych , które są opisane poniżej . Indeksy „stare” i „nowe” zostały wybrane, ponieważ jest zwyczajem, aby zapoznać się i jako starego zasadach i nowej podstawie , odpowiednio. Przydatne jest opisywanie starych współrzędnych w kategoriach nowych, ponieważ ogólnie rzecz biorąc, istnieją wyrażenia obejmujące stare współrzędne i jeśli chce się uzyskać równoważne wyrażenia w kategoriach nowych współrzędnych; uzyskuje się to poprzez zastąpienie starych współrzędnych ich wyrażeniami w postaci nowych współrzędnych. ${\ Displaystyle B_ {\ tekst {stary}} = (\ mathbf {v} _ {1}, \ ldots, \ mathbf {v} _ {n})}$${\ Displaystyle B_ {\ tekst {nowy}} = (\ mathbf {w} _ {1}, \ ldots, \ mathbf {w} _ {n})}$${\displaystyle B_{\mathrm {stary}}}$${\displaystyle B_{\mathrm {nowy}}.}$${\displaystyle B_{\mathrm {stary}}}$${\displaystyle B_{\mathrm {nowy}}}$

Zazwyczaj nowe wektory bazowe są podawane przez ich współrzędne w stosunku do starej bazy, czyli

${\ Displaystyle \ mathbf {w} _ {j} = \ suma _ {i = 1} ^ {n} a_ {i, j} \ mathbf {v} _ {i}}.$

Jeśli i są współrzędnymi wektora x odpowiednio nad starą i nową bazą, wzór na zmianę bazy jest ${\ Displaystyle (x_ {1}, \ ldots, x_ {n})}$${\displaystyle (y_{1},\ldots,y_{n})}$

${\ Displaystyle x_ {i} = \ suma _ {j = 1} ^ {n} a_ {i, j} y_ {j}}$

dla i = 1, …, n .

Wzór ten można zwięźle zapisać w notacji macierzowej . Niech A będzie macierzą , i ${\displaystyle a_{i,j}}$

${\ Displaystyle X = {\ zacząć {bmatrix} x_ {1} \ \ \ vdots \ \ x_ {n} \ koniec {bmatrix}} \ quad {\ tekst {i}} \ quad Y = {\ zacząć {bmatrix} y_{1}\\\vdots \\y_{n}\end{bmatryca}}}$

być wektorami kolumnowymi współrzędnych v odpowiednio w starej i nowej podstawie, to wzór na zmianę współrzędnych jest

${\ Displaystyle X = AY.}$

Wzór można udowodnić, rozważając rozkład wektora x na dwóch bazach: jeden ma

${\ Displaystyle \ mathbf {x} = \ suma _ {i = 1} ^ {n} x_ {i} \ mathbf {v} _ {i}}$

oraz

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {x} & = \ suma _ {j = 1} ^ {n} y_ {j} \ mathbf {w} _ {j} \ \ & = \ suma _ {j =1}^{n}y_{j}\sum _{i=1}^{n}a_{i,j}\mathbf {v} _{i}\\&=\sum _{i=1} ^{n}\left(\sum _{j=1}^{n}a_{i,j}y_{j}\right)\mathbf {v} _{i}.\end{wyrównany}}}$

Wzór na zmianę bazy wynika więc z jednoznaczności rozkładu wektora na bazę, tutaj ; to jest ${\displaystyle B_{\tekst{stary}}}$

${\ Displaystyle x_ {i} = \ suma _ {j = 1} ^ {n} a_ {i, j} y_ {j}}$

dla i = 1, …, n .

Powiązane pojęcia

Darmowy moduł

Zastąpienie pola występującego w definicji przestrzeni wektorowej pierścieniem daje definicję modułu . W przypadku modułów niezależność liniowa i zbiory rozpinające są definiowane dokładnie tak, jak dla przestrzeni wektorowych, chociaż „ zbiór generujący ” jest częściej używany niż „zbiór rozpinający”.

Podobnie jak w przypadku przestrzeni wektorowych, bazą modułu jest liniowo niezależny podzbiór będący jednocześnie zbiorem generującym. Główna różnica w stosunku do teorii przestrzeni wektorowych polega na tym, że nie każdy moduł ma podstawę. Moduł, który ma podstawę, nazywany jest modułem wolnym . Wolne moduły odgrywają fundamentalną rolę w teorii modułów, ponieważ mogą być używane do opisywania struktury niewolnych modułów poprzez wolne rozdzielczości .

Moduł nad liczbami całkowitymi to dokładnie to samo, co grupa abelowa . Zatem wolny moduł nad liczbami całkowitymi jest również wolną grupą abelową. Wolne grupy abelowe mają określone właściwości, które nie są współdzielone przez moduły z innymi pierścieniami. W szczególności, każda podgrupa wolnej grupy Abelowych jest wolna grupa abelowa i jeśli G jest podgrupa o skończonej generowania wolnych Abelowych grupy H (czyli grupa przemienna który ma skończoną masy), jest podstawą z H i liczba całkowita 0 ≤ k ≤ n taka, która jest podstawą G , dla niektórych niezerowych liczb całkowitych . Aby uzyskać szczegółowe informacje, zobacz Swobodna grupa abelowa § Podgrupy . ${\ Displaystyle \ mathbf {e} _ {1} \ ldots \ mathbf {e} _ {n}}$${\ Displaystyle a_ {1} \ mathbf {e} _ {1}, \ ldots, a_ {k} \ mathbf {e} _ {k}}$${\displaystyle a_{1},\ldots,a_{k}}$

Analiza

W kontekście nieskończenie wymiarowych przestrzeni wektorowych nad liczbami rzeczywistymi lub zespolonymi, termin Baza Hamela (nazwana na cześćGeorga Hamela) lubbaza algebraicznamoże być użyta w odniesieniu do bazy zdefiniowanej w tym artykule. Ma to na celu odróżnienie od innych pojęć „podstawy”, które istnieją, gdy nieskończenie wymiarowe przestrzenie wektorowe są wyposażone w dodatkową strukturę. Najważniejszymi alternatywami sąbazy ortogonalnenaprzestrzeniach Hilberta,bazy Schauderaibazy Markuszewiczanaunormowanych przestrzeniach liniowych. W przypadku liczb rzeczywistychRrozpatrywanych jako przestrzeń wektorowa nadciałemQliczb wymiernych, bazy Hamela są niepoliczalne i mają w szczególnościmockontinuum, czyliliczbę kardynalną ,gdziejest najmniejszym nieskończonym kardynałem, czyli kardynałem. liczb całkowitych. ${\ Displaystyle 2 ^ {\ aleph _ {0}}}$${\displaystyle \aleph_{0}}$

Wspólną cechą innych pojęć jest to, że pozwalają na branie nieskończonych kombinacji liniowych wektorów bazowych w celu wygenerowania przestrzeni. To, oczywiście, wymaga nieskończone sumy są sensownie zdefiniowane na tych przestrzeniach, jak to ma miejsce w przypadku topologicznych przestrzeni wektorowych - duża klasa przestrzeni wektorowych tym np przestrzeni Hilberta , przestrzenie Banacha , lub spacjami Frecheta .

Preferencja innych typów baz dla przestrzeni nieskończenie wymiarowych jest uzasadniona faktem, że baza Hamela staje się „zbyt duża” w przestrzeniach Banacha: Jeśli X jest nieskończenie wymiarową przestrzenią unormowaną wektorową, która jest zupełna (tzn. X jest przestrzenią Banacha ), to każda podstawa Hamela X jest z konieczności niepoliczalna . Jest to konsekwencja twierdzenia Baire'a o kategorii . Kompletność oraz nieskończony wymiar są kluczowymi założeniami poprzedniego twierdzenia. Rzeczywiście, przestrzenie skończenie wymiarowe mają z definicji skończone bazy i istnieją nieskończenie wymiarowe ( niekompletne ) przestrzenie unormowane, które mają policzalne bazy Hamela. Rozważmy , przestrzeń z sekwencji liczb rzeczywistych, które mają tylko skończenie wiele niezerowe elementy, z normą . Jego standardowa baza , składająca się z sekwencji zawierających tylko jeden niezerowy element, który jest równy 1, jest policzalną bazą Hamela. ${\displaystyle c_{00}}$ ${\ Displaystyle x = (x_ {n})}$${\textstyle \|x\|=\sup _{n}|x_{n}|}$

Przykład

W badaniu szeregów Fouriera dowiadujemy się, że funkcje {1} ∪ { sin( nx ), cos( nx ): n = 1, 2, 3, … } są „bazą ortogonalną” (rzeczywistego lub zespolonego) przestrzeni wektorowej wszystkich funkcji (o wartościach rzeczywistych lub zespolonych) na przedziale [0, 2π], które są całkowalne kwadratowo na tym przedziale, tj. funkcje f spełniające

${\ Displaystyle \ int _ {0} ^ {2 \ pi} \ lewo | f (x) \ prawo | ^ {2} \ dx < \ infty.}$

Funkcje {1} ∪ { sin( nx ), cos( nx ): n = 1, 2, 3, … } są liniowo niezależne, a każda funkcja f, która jest całkowalna do kwadratu na [0, 2π] jest „nieskończoną liniowa kombinacja” z nich, w tym sensie, że

${\ Displaystyle \ lim _ {n \ do \ infty} \ int _ {0} ^ {2 \ pi} \ lewo | a_ {0}+ \ suma _ {k = 1} ^ {n} \ lewo (a_ { k}\cos \left(kx\right)+b_{k}\sin \left(kx\right)\right)-f(x)\right|^{2}dx=0}$

dla odpowiednich (rzeczywistych lub zespolonych) współczynników a _k , b _k . Ale wiele funkcji całkowalnych z kwadratem nie może być przedstawionych jako skończone kombinacje liniowe tych funkcji bazowych, które dlatego nie zawierają bazy Hamela. Każda baza Hamel w tej przestrzeni jest znacznie większa niż ten zaledwie przeliczalnie nieskończony zestaw funkcji. Bazy Hamela tego typu przestrzeni są zazwyczaj nieprzydatne, podczas gdy bazy ortonormalne tych przestrzeni są niezbędne w analizie Fouriera .

Geometria

Geometryczne pojęcia w afinicznej przestrzeni , przestrzeni rzutowej , wypukłą zestawu i stożek posiada związane pojęcia podstawa . Afinicznej podstawę dla n -wymiarowej przestrzeni afinicznej jest punkty ogólnego położenia liniowego . A${\displaystyle n+1}$podstawą rzutową sąpunkty w położeniu ogólnym, w przestrzeni rzutowej o wymiarzen. A${\displaystyle n+2}$wypukła podstawa zPolytopejest zbiorem wierzchołków jejwypukłej. APodstawa stożka składa się z jednego punktu po krawędzi wielokątnego stożka. Zobacz takżepodstawę Hilberta (programowanie liniowe).

Podstawa losowa

Dla rozkładu prawdopodobieństwa w R ⁿ z funkcją gęstości prawdopodobieństwa , takiego jak równowaga w n- wymiarowej kuli względem miary Lebesgue'a, można wykazać, że n losowo i niezależnie wybranych wektorów utworzy bazę o prawdopodobieństwie 1 , które jest ze względu na to, że n wektorów zależnych liniowo x ₁ , …, x _n w R ⁿ powinno spełniać równanie det[ x ₁ ⋯ x _n ] = 0 (zerowy wyznacznik macierzy z kolumnami x _i ) oraz zbiór zer wielomianu nietrywialnego ma miarę zerową. Ta obserwacja doprowadziła do opracowania technik aproksymacji zasad losowych.

Empiryczny rozkład długości N parami prawie ortogonalnych łańcuchów wektorów, które są niezależnie losowo próbkowane z n- wymiarowego sześcianu [−1,1] ⁿ w funkcji wymiaru, n . Wykresy pudełkowe pokazują drugi i trzeci kwartyl tych danych dla każdego n , czerwone słupki odpowiadają medianom, a niebieskie gwiazdki oznaczają średnie. Czerwona krzywa przedstawia teoretyczne ograniczenie podane przez równanie. (1) a zielona krzywa pokazuje doprecyzowane oszacowanie.

Trudno jest numerycznie sprawdzić zależność liniową lub dokładną ortogonalność. Dlatego używane jest pojęcie ε-ortogonalności. Na przestrzeni produktu z wewnętrzną , x znaczy ε-ortogonalne do Y , jeśli (to jest, cosinusa kąta między X i Y jest mniejszy niż ε ). ${\ Displaystyle \ lewo | \ lewo \ langle x, y \ prawo \ rangle \ prawo |/ \ lewo (\ lewo \ | x \ prawo \ | \ lewo \ | y \ prawo \ | \ prawo) < \ varepsilon }$

W wysokich wymiarach dwa niezależne wektory losowe są z dużym prawdopodobieństwem prawie ortogonalne, a liczba niezależnych wektorów losowych, z których wszystkie są z dużym prawdopodobieństwem parami prawie ortogonalne, rośnie wykładniczo z wymiarem. Dokładniej, rozważ równomierny rozkład w n- wymiarowej kuli. Wybierz N niezależnych losowych wektorów z kuli (są niezależne i identycznie rozmieszczone ). Niech θ będzie małą liczbą dodatnią. Następnie dla

${\ Displaystyle N \ leq e ^ {\ Frac {\ epsilon ^ {2} n} {4}} [- \ ln (1-\ theta)] ^ {\ Frac {1} {2}}}$

(Równanie 1)

N wektorów losowych jest parami ε-ortogonalnych z prawdopodobieństwem 1 − θ . Ten wzrost N wykładniczo z wymiarem n i dla wystarczająco dużego n . Ta właściwość zasad losowych jest przejawem zjawiska tzw. koncentracji miarowej . ${\ Displaystyle N \ gg n}$

Rysunek (po prawej) ilustruje rozkład długości N parami prawie ortogonalnych łańcuchów wektorów, które są niezależnie losowo próbkowane z n- wymiarowego sześcianu [−1,1] ⁿ w funkcji wymiaru, n . Punkt jest najpierw losowo wybierany w kostce. Drugi punkt jest losowo wybierany w tej samej kostce. Jeśli kąt między wektorami mieścił się w zakresie π/2 ± 0,037π/2, wektor został zachowany. W następnym kroku nowy wektor jest generowany w tym samym hipersześcianie i oceniane są jego kąty z poprzednio wygenerowanymi wektorami. Jeśli te kąty mieszczą się w zakresie π/2 ± 0,037π/2, wektor jest zachowywany. Proces jest powtarzany aż do zerwania łańcucha prawie ortogonalności i rejestrowana jest liczba takich parami prawie ortogonalnych wektorów (długość łańcucha). Dla każdego n , 20 parami prawie ortogonalnych łańcuchów zostało skonstruowanych numerycznie dla każdego wymiaru. Przedstawiono rozkład długości tych łańcuchów.

Dowód, że każda przestrzeń wektorowa ma podstawę

Niech V będzie dowolną przestrzenią wektorową nad jakimś ciałem F . Niech X będzie zbiorem wszystkich liniowo niezależnych podzbiorów V .

Zbiór X jest niepusty, ponieważ pusty zbiór jest niezależnym podzbiorem V i jest częściowo uporządkowany przez inkluzję, która jest oznaczona, jak zwykle, przez ⊆ .

Niech Y będzie podzbiorem X, który jest całkowicie uporządkowany przez ⊆ , i niech L _Y będzie sumą wszystkich elementów Y (które same są pewnymi podzbiorami V ).

Ponieważ ( Y , ⊆) jest całkowicie uporządkowane, każdy skończony podzbiór L _Y jest podzbiorem elementu Y , który jest liniowo niezależnym podzbiorem V , a zatem L _Y jest liniowo niezależny. Zatem L _Y jest elementem X . Dlatego L _Y jest górnym ograniczeniem dla Y w ( X , ⊆ ): jest to element X , który zawiera każdy element Y .

Ponieważ X jest niepuste, a każdy całkowicie uporządkowany podzbiór ( X , ⊆) ma górne ograniczenie w X , lemat Zorna zakłada, że X ma element maksymalny. Innymi słowy, istnieje element L _max z X spełniający warunek, że ilekroć L _max ⊆ L dla jakiegoś elementu L z X , wtedy L = L _max .

Pozostaje udowodnić, że L _max jest bazą V . Ponieważ L _max należy do X , wiemy już, że L _max jest liniowo niezależnym podzbiorem V .

Gdyby nie było pewne wektor wag z V , które nie znajduje się w odstępie L _max , a w nie być elementem L _max obu. Niech L _w = L _max ∪ { w }. Zbiór ten jest elementem X , to znaczy jest liniowo niezależnym podzbiorem V (ponieważ w nie należy do zakresu L _max , a L _max jest niezależne). Ponieważ L _max ⊆ L _w , i L _max ≠ L _w (ponieważ L _w zawiera wektor w, który nie jest zawarty w L _max ), przeczy to maksymalizacji L _max . To pokazuje, że L _max obejmuje V .

Stąd L _max jest liniowo niezależna i obejmuje V . Jest to więc baza V , a to dowodzi, że każda przestrzeń wektorowa ma bazę.

Dowód ten opiera się na lemie Zorna, który jest odpowiednikiem aksjomatu wyboru . I odwrotnie, udowodniono, że jeśli każda przestrzeń wektorowa ma bazę, to aksjomat wyboru jest prawdziwy. Zatem te dwa twierdzenia są równoważne.

Zobacz też

• Podstawa matroidu
• Zmiana bazy  – Zmiana współrzędnych dla przestrzeni wektorowej
• Rama przestrzeni wektorowej
• Podstawa sferyczna  – podstawa służąca do wyrażania tensorów sferycznych

Uwagi

Bibliografia

Ogólne odniesienia

• Blass, Andreas (1984), „Istnienie zasad implikuje aksjomat wyboru”, Aksjomatyczna teoria mnogości (PDF) , Współczesna Matematyka tom 31 , Providence, RI: American Mathematical Society , s. 31-33, ISBN 978-0-8218-5026-8, MR  0763890
• Brown, William A. (1991), Macierze i przestrzenie wektorowe , New York: M. Dekker, ISBN 978-0-8247-8419-5
• Lang, Serge (1987), algebra liniowa , Berlin, New York: Springer-Verlag , ISBN 978-0-387-96412-6

odniesienia historyczne

• Banach, Stefan (1922), „Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (O operacjach w zbiorach abstrakcyjnych i ich zastosowaniu do równań całkowych)” (PDF) , Fundamenta Mathematicae (w języku francuskim), 3 : 133– 181, doi : 10.4064/fm-3-1-133-181 , ISSN  0016-2736
• Bolzano Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Rozważania niektórych aspektów elementarnej geometrii) (w języku niemieckim)
• Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elementy historii matematyki) (w języku francuskim), Paryż: Hermann
• Dorier, Jean-Luc (1995), „Ogólny zarys genezy teorii przestrzeni wektorowej” , Historia Mathematica , 22 (3): 227-261, doi : 10.1006/hmat.1995.1024 , MR  1347828
• Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (w języku francuskim), Chez Firmin Didot, père et fils
• Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (w języku niemieckim), przedruk: Hermann Grassmann. Tłumaczone przez Lloyda C. Kannenberga. (2000), Teoria Rozszerzeń , Kannenberg, LC, Providence, RI: Amerykańskie Towarzystwo Matematyczne , ISBN 978-0-8218-2031-5
• Hamel, Georg (1905), „Eine Basis aller Zahlen und die unstetigen Lösungen der Funktionalgleichung f (x + y) = f (x) + f (y)” , Mathematische Annalen (w języku niemieckim), Lipsk, 60 : 459-462
• Hamilton, William Rowan (1853), Wykłady na temat kwaternionów , Królewska Akademia Irlandzka
• Möbiusa, August Ferdinand (1827), Der Barycentrische Calcul: ein neues Hülfsmittel zur Behandlung der Geometrie analytischen (barycentryczne rachunek: nowe narzędzie do obróbki analitycznej geometrii) (w języku niemieckim), zarchiwizowane z oryginałem na 2009-04-12
• Moore, Gregory H. (1995), „Aksjomatyzacja algebry liniowej: 1875-1940”, Historia Mathematica , 22 (3): 262-303, doi : 10.1006/hmat.1995.1025
• Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (w języku włoskim), Turyn

Zewnętrzne linki

• Filmy instruktażowe z Khan Academy
  • Wprowadzenie do podstaw podprzestrzeni
  • Dowód, że każda baza podprzestrzenna ma taką samą liczbę elementów
• "Kombinacje liniowe, wektory rozpiętości i bazowe" . Istota algebry liniowej . 6 sierpnia 2016 – przez YouTube .
• "Podstawa" , Encyklopedia Matematyki , EMS Press , 2001 [1994]