Koperta (matematyka) - Envelope (mathematics)

W geometrii An koperty z płaskiej rodziny krzywych jest krzywą , która jest styczna do każdego członka rodziny w pewnym punkcie, a te punkty styczności ze sobą tworząc całą powłokę. Klasycznie, punkt na obwiedni może być traktowany jako przecięcie dwóch „ nieskończenie przyległych” krzywych, co oznacza granicę przecięć sąsiednich krzywych. Ten pomysł można uogólnić na obwiednię powierzchni w przestrzeni i tak dalej na wyższe wymiary.

Aby mieć obwiednię, konieczne jest, aby poszczególne elementy rodziny krzywych były krzywymi różniczkalnymi, ponieważ pojęcie styczności nie ma zastosowania w przeciwnym razie, a przejście między elementami musi przebiegać płynnie . Ale te warunki nie są wystarczające – dana rodzina może nie mieć koperty. Prostym tego przykładem jest rodzina koncentrycznych okręgów o rozszerzającym się promieniu.

Koperta rodziny krzywych

Niech każda krzywa C _T w rodzinie podawać jako rozwiązanie równania f _t ( x ,  y ) = 0 (patrz niejawnego krzywą ), w którym T oznacza parametrów. Napisać F ( t ,  x ,  y ) = f _t ( x ,  y ) i odpowiada M jest różniczkowalną.

Obwiednia rodziny C _t jest wtedy zdefiniowana jako zbiór punktów ( x , y ), dla których jednocześnie ${\displaystyle {\mathcal {D}}}$

${\ Displaystyle F (t, x, y) = 0 ~ ~ {\ mathsf {i}} ~ ~ {\ częściowy F \ nad \ częściowy t} (t, x, y) = 0}$

jakiegoś wartości T , w której jest częściowo pochodną z F, w stosunku do t . ${\ Displaystyle \ częściowe F/\ częściowe t}$

Jeżeli t i u , t ≠ u są dwiema wartościami parametru to przecięcie krzywych C _t i C _u jest określone wzorem

${\ Displaystyle F (t, x, y) = F (u, x, y) = 0 \,}$

lub równoważnie

${\ Displaystyle F (t, x, y) = 0 ~ ~ {\ mathsf {i}} ~ ~ {\ Frac {F (u, x, y) - F (t, x, y)} {ut}} =0.}$

Niech u → t daje powyższą definicję.

Ważnym szczególnym przypadkiem jest sytuacja, w której F ( t ,  x ,  y ) jest wielomianem w t . Obejmuje to, usuwając mianowniki , przypadek, w którym F ( t ,  x ,  y ) jest funkcją wymierną w t . W tym przypadku, określenie wynosi t oznacza podwójne korzeń F ( t ,  x ,  y ), a więc równanie koperty można znaleźć ustawienia wyróżnik o F 0 (ponieważ definicja wymaga M = 0 w niektórych t i pierwsza pochodna =0 tj. jej wartość 0 i wynosi min/max w tym t).

Na przykład, niech C _t być linię, której x i y przechwytuje się t i 11- T , jest pokazany w animacji powyżej. Równanie C _t to

${\ Displaystyle {\ Frac {x} {t}} + {\ Frac {y} {11-t}} = 1}$

lub rozliczenie ułamków,

${\ Displaystyle x (11-t) + yt-t (11-t) = t ^ {2} + (-x + y-11) t + 11x = 0. \,}$

Równanie obwiedni to

${\ Displaystyle (-x + y-11) ^ {2}-44x = (xy) ^ {2}-22 (x + y) + 121 = 0. \,}$

Często, gdy F nie jest wymierną funkcją parametru, można ją sprowadzić do tego przypadku przez odpowiednie podstawienie. Na przykład, jeśli rodzina jest podana przez C _θ z równaniem postaci u ( x ,  y )cos θ + v ( x ,  y )sin θ= w ( x ,  y ), to t = e ^{i θ} , cos θ=( t +1/ t )/2, sin θ=( t -1/ t )/2 i zmienia równanie krzywej na

${\ Displaystyle u {1 \ ponad 2} (t + {1 \ nad t}) + v {1 \ nad 2i} (t- {1 \ nad t}) = w}$

lub

${\ Displaystyle (u-iv) t ^ {2} -2 WT + (u + IV) = 0. \,}$

Równanie obwiedni jest następnie podane przez ustawienie dyskryminatora na 0:

${\ Displaystyle (u-iv) (u + IV)-w ^ {2} = 0 \,}$

lub

${\ Displaystyle u ^ {2} + v ^ {2} = w ^ {2}. \,}$

Alternatywne definicje

1. Obwiednia E ₁ to granica przecięć pobliskich krzywych C _t .
2. Obwiednia E ₂ jest krzywą styczną do wszystkich C _t .
3. Obwiednia E ₃ jest granicą obszaru wypełnionego krzywymi C _t .

Następnie , i , gdzie jest zbiorem punktów zdefiniowanych na początku sekcji nadrzędnej tej podsekcji. ${\displaystyle E_{1}\subseteq {\mathcal {D}}}$${\displaystyle E_{2}\subseteq {\mathcal {D}}}$${\displaystyle E_{3}\subseteq {\mathcal {D}}}$${\displaystyle {\mathcal {D}}}$

Przykłady

Przykład 1

Definicje te E ₁ , E ₂ , a E ₃ otoczki mogą być różne zestawy. Rozważmy na przykład krzywą y = x ³ sparametryzowaną przez γ : R → R ² gdzie γ( t ) = ( t , t ³ ) . Jednoparametrowa rodzina krzywych zostanie podana przez linie styczne do γ.

Najpierw obliczamy dyskryminator . Funkcja generująca to ${\displaystyle {\mathcal {D}}}$

${\ Displaystyle F (t (x, y)) = 3t ^ {2}xy-2t ^ {3}.}$

Obliczanie pochodnej cząstkowej F _t = 6 t ( x – t ) . Wynika z tego, że albo x = t albo t = 0 . Najpierw załóżmy, że x = t i t ≠ 0 . Podstawiając do F: i tak, zakładając, że t ≠ 0, wynika z tego, że F = F _t = 0 wtedy i tylko wtedy, gdy ( x , y ) = ( t , t ³ ) . Następnie zakładając, że t = 0 i podstawiając do F, otrzymujemy F (0,( x , y )) = − y . Tak więc, zakładając t = 0 , wynika z tego, że F = F _t = 0 wtedy i tylko wtedy, gdy y = 0 . Zatem wyróżnikiem jest pierwotna krzywa i jej styczna w γ(0): ${\displaystyle F(t(t,y))=t^{3}-y\,}$

${\ Displaystyle {\ mathcal {D}} = \ {(x, y) \ w \ mathbb {R} ^ {2}: y = x ^ {3} \} \ filiżanka \ {(x, y) \ w \mathbb {R} ^{2}:y=0\}\ .}$

Następnie obliczamy E ₁ . Jedna krzywa jest dana przez F ( t , ( x , y )) = 0 a pobliska krzywa jest dana przez F ( t + ε, ( x , y )) gdzie ε jest bardzo małą liczbą. Punkt przecięcia pochodzi od spojrzenia na granicę F ( t , ( x , y )) =  F ( t + ε, ( x , y )) gdy ε dąży do zera. Zauważ, że F ( t ,( x , y )) =  F ( t + ε,( x , y )) wtedy i tylko wtedy

${\displaystyle L:=F(t,(x,y))-F(t+\varepsilon,(x,y))=2\varepsilon ^{3}+6\varepsilon t^{2}+6\varepsilon ^{2}t-(3\varepsilon ^{2}+6\varepsilon t)x=0.}$

Jeśli t ≠ 0 to L ma tylko jeden czynnik ε. Zakładając, że t ≠ 0 to przecięcie jest dane przez

${\ Displaystyle \ lim _ {\ varepsilon \ do 0} {\ Frac {1} {\ varepsilon}} L = 6t (tx) \.}$

Ponieważ t ≠ 0 wynika, że x = t . Wartość y jest obliczana wiedząc, że ten punkt musi leżeć na linii stycznej do oryginalnej krzywej γ: że F ( t ,( x , y )) = 0 . Podstawianie i rozwiązywanie daje y = t ³ . Gdy t = 0 , L jest podzielne przez ε ² . Zakładając, że t = 0 to przecięcie jest dane przez

${\ Displaystyle \ Lim _ {\ varepsilon \ do 0} {\ Frac {1} {\ varepsilon ^ {2}}} L = 3x \.}$

Wynika z tego, że x = 0 , a wiedząc, że F ( t ,( x , y )) = 0 daje y = 0 . Wynika, że

${\ Displaystyle E_ {1} = \ {(x, y) \ w \ mathbb {R} ^ {2}: y = x ^ {3} \} \.}$

Następnie obliczamy E ₂ . Sama krzywa jest krzywą styczną do wszystkich własnych linii stycznych. Wynika, że

${\ Displaystyle E_ {2} = \ {(x, y) \ w \ mathbb {R} ^ {2}: y = x ^ {3} \} \.}$

Na koniec obliczamy E ₃ . Każdy punkt na płaszczyźnie ma co najmniej jedną styczną do γ przechodzącą przez niego, a więc obszar wypełniony przez styczne jest całą płaszczyzną. Granica E ₃ jest więc zbiorem pustym. Rozważmy punkt na płaszczyźnie, powiedzmy ( x ₀ , y ₀ ). Ten punkt leży na linii stycznej wtedy i tylko wtedy, gdy istnieje t takie, że

${\ Displaystyle F (t (x_ {0}, y_ {0})) = 3 t ^ {2} x_ {0}-y_ {0}-2 t ^ {3} = 0 \ .}$

To jest sześcienny w t i jako taki ma co najmniej jedno rzeczywiste rozwiązanie. Wynika z tego, że co najmniej jedna prosta styczna do γ musi przechodzić przez dowolny punkt na płaszczyźnie. Jeśli y > x ³ i y > 0 to każdy punkt ( x , y ) ma dokładnie jedną styczną do γ przechodzącą przez niego. To samo jest prawdziwe, jeśli y < x ³ y < 0 . Jeśli y < x ³ i y > 0 to każdy punkt ( x , y ) ma dokładnie trzy różne proste styczne do γ przechodzące przez niego. To samo jest prawdziwe, jeśli y > x ³ i y < 0 . Jeśli y = x ³ i y ≠ 0 to każdy punkt ( x , y ) ma dokładnie dwie styczne do γ przechodzące przez niego (odpowiada to sześciennemu mającemu jeden zwykły pierwiastek i jeden powtarzający się pierwiastek). To samo jest prawdziwe, jeśli y ≠ x ³ i y = 0 . Jeśli y = x ³ i x = 0 , tj. x = y = 0 , to punkt ten ma przechodzącą przez niego pojedynczą prostą styczną do γ (odpowiada to sześciennemu mającemu jeden pierwiastek rzeczywisty z wielokrotności 3). Wynika, że

${\displaystyle E_{3}=\varnic .}$

Przykład 2

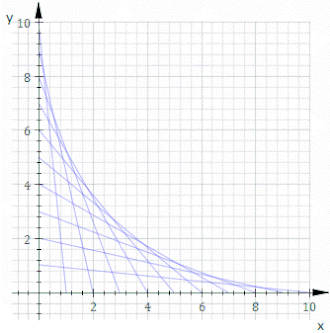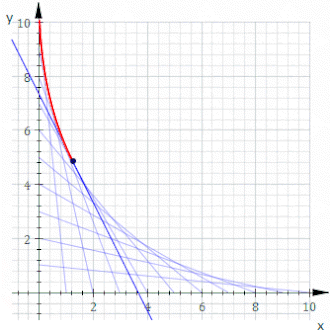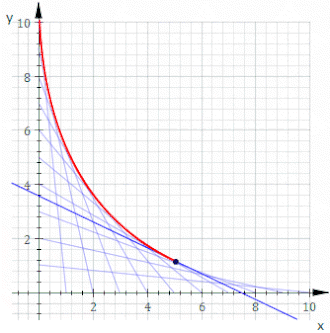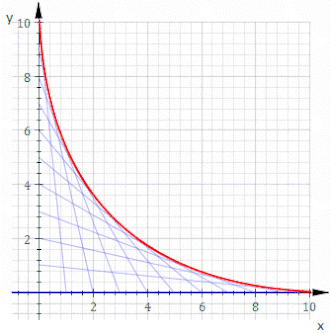
W sztuce strun powszechne jest krzyżowe łączenie dwóch linii równo rozmieszczonych szpilek. Jaka krzywa powstaje?

Dla uproszczenia ustaw szpilki na osiach x i y ; nie- prostopadły układ jest obracanie i skalowanie z dala. Ogólny wątek liniowy łączy dwa punkty (0, k − t ) i ( t , 0), gdzie k jest dowolną stałą skalowania, a rodzina linii jest generowana przez zmianę parametru t . Z prostej geometrii równanie tej prostej to y = −( k  −  t ) x / t + k  −  t . Przestawianie i odlewanie w postaci F ( x , y , t ) = 0 daje:

${\ Displaystyle F (x, y, t) = - {\ Frac {kx} {t}} - t + x + ky = 0 \,}$

(1)

Teraz rozróżnij F ( x , y , t ) względem t i ustaw wynik równy zero, aby otrzymać

${\ Displaystyle {\ Frac {\ częściowy F (x, y, t)} {\ częściowy t}} = {\ Frac {kx} {t ^ {2}}} -1 = 0 \,}$

(2)

Te dwa równania wspólnie definiują równanie obwiedni. Z (2) mamy:

${\displaystyle t={\sqrt {kx}}\,}$

Podstawienie tej wartości t do (1) i uproszczenie daje równanie dla obwiedni:

${\ Displaystyle y = ({\ sqrt {x}} - {\ sqrt {k}}) ^ {2} \,}$

(3)

Lub przestawiając się na bardziej elegancką formę, która pokazuje symetrię między x i y:

${\ Displaystyle {\ sqrt {x}} + {\ sqrt {y}} = {\ sqrt {k}}}$

(4)

Możemy wykonać obrót osi, gdzie oś b jest linią y=x skierowaną na północny wschód, a oś a jest linią y=-x skierowaną na południowy wschód. Te nowe osie są powiązane z oryginalnymi osiami xy przez x=(b+a)/ √ 2 i y=(ba)/ √ 2 . Otrzymujemy, po podstawieniu do (4) oraz rozszerzeniu i uproszczeniu,

${\ Displaystyle b = {\ Frac {1} {k {\ sqrt {2}}}} a ^ {2} + {\ Frac {k} {2 {\ sqrt {2}}}}}$,

(5)

co jest najwyraźniej równaniem paraboli o osi wzdłuż a=0 , lub y=x .

Przykład 3

Niech I ⊂ R będzie przedziałem otwartym i niech γ : I → R ² będzie gładką krzywą płaską sparametryzowaną długością łuku . Rozważ jednoparametrową rodzinę linii normalnych do γ( I ). Prosta jest normalna do γ w γ( t ), jeśli przechodzi przez γ( t ) i jest prostopadła do wektora stycznego do γ w γ( t ). Niech T oznacza jednostkowy wektor styczny do γ i niech N oznacza jednostkowy wektor normalny . Używając kropki do oznaczenia iloczynu skalarnego , rodzina tworząca dla jednoparametrowej rodziny prostych jest dana przez F  : I × R ² → R gdzie

${\ Displaystyle F (t {\ mathbf {x}}) = ({\ mathbf {x}} - \ gamma (t)) \ cdot {\ mathbf {T}} (t) \}$

Oczywiście ( x − γ)· T = 0 wtedy i tylko wtedy, gdy x − γ jest prostopadłe do T lub równoważnie, wtedy i tylko wtedy, gdy x − γ jest równoległe do N , lub równoważnie, wtedy i tylko wtedy, gdy x = γ + λ N dla niektórych λ ∈ R . Wynika, że

${\ Displaystyle L_ {t_ {0}}: = \ {{\ mathbf {x}} \ w \ mathbb {R} ^ {2}: F (t_ {0}, {\ mathbf {x}}) = 0 \}}$

jest dokładnie normalną linią do γ w γ( t ₀ ). Aby znaleźć wyróżnik F , musimy obliczyć jego pochodną cząstkową względem t :

${\ Displaystyle {\ Frac {\ częściowy F}{\ częściowy t}} (t {\ mathbf {x}}) = \ kappa (t) ({\ mathbf {x}} - \ gamma (t))\ cdot {\mathbf {N} }(t)-1\ ,}$

gdzie κ jest krzywizną krzywej płaskiej γ. Zaobserwowano, że F = 0 wtedy i tylko wtedy, gdy x - γ = λ N dla pewnego λ ∈ R . Zakładając, że F = 0 daje

${\ Displaystyle {\ Frac {\ częściowy F} {\ częściowy t}} = \ lambda \ kappa (t) -1 \ .}$

Zakładając, że κ ≠ 0 wynika, że ​​λ = 1/κ i tak

${\ Displaystyle {\ mathcal {D}} = \ gamma (t) + {\ Frac {1} {\ kappa (t)}} {\ mathbf {N}} (t) \}$

To jest dokładnie rozwinięcie krzywej γ.

Przykład 4

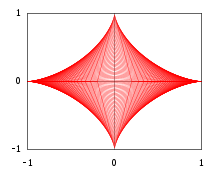
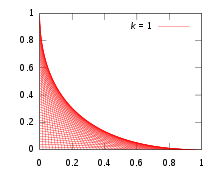
Poniższy przykład pokazuje, że w niektórych przypadkach obwiednia rodziny krzywych może być postrzegana jako topologiczna granica połączenia zbiorów, której granicami są krzywe obwiedni. Dla i rozważyć (Otwarte) trójkąt prostokątny w płaszczyźnie kartezjańskiej z wierzchołków , a${\displaystyle s>0}$${\displaystyle t>0}$${\ Displaystyle (0,0)}$${\displaystyle (s,0)}$${\ Displaystyle (0, t)}$

${\ Displaystyle T_ {s, t}: = \ lewo \ {(x, y) \ w \ mathbb {R} _ {+} ^ {2}: \ {\ Frac {x} {s}} + {\ szczelina {y}{t}}<1\prawo\}.}$

Ustal wykładnik i rozważ sumę wszystkich trójkątów podlegających ograniczeniu , czyli zbiór otwarty open ${\ Displaystyle \ alfa > 0}$${\displaystyle T_{s,t}}$${\ Displaystyle \ textstyle s ^ {\ alfa} + t ^ {\ alfa} = 1}$

${\ Displaystyle \ Delta _ {\ alfa}: = \ bigcup _ {s ^ {\ alfa} + t ^ {\ alfa} = 1} T_ {s, t}.}$

Aby napisać reprezentację kartezjańską dla , zacznij od dowolnego , satysfakcjonującego i dowolnego . Höldera nierówność w stosunku do sprzężonego wykładników i otrzymujemy: ${\ Displaystyle \ textstyle \ Delta _ {\ alfa}}$${\displaystyle \textstyle s>0}$${\displaystyle \textstyle t>0}$${\ Displaystyle \ textstyle s ^ {\ alfa} + t ^ {\ alfa} = 1}$${\ Displaystyle \ textstyle (x, y) \ w \ mathbb {R} _ {+} ^ {2}}$${\ Displaystyle \ textstyle \ mathbb {R} ^ {2}}$${\ Displaystyle p: = 1 + {\ Frac {1} {\ alfa}}}$${\ Displaystyle \ textstyle q: = {1+ \ alfa}}$

${\ Displaystyle x ^ {\ Frac {\ alfa} {\ alfa +1}} + Y ^ {\ Frac {\ alfa} {\ alfa +1}} \ leq \ lewo ({\ Frac {x} {s} }+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}{\Duża (}s^{\alpha }+t^{\alpha }{\ Duży )}^{\frac {1}{\alpha +1}}=\left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac { \alfa }{\alfa +1}}}$,

z równością wtedy i tylko wtedy, gdy . W kategoriach unii zbiorów ta ostatnia nierówność brzmi: punkt należy do zbioru , to znaczy należy do niektórych z , wtedy i tylko wtedy, gdy spełnia ${\ Displaystyle \ textstyle s: \ t = x ^ {\ Frac {1} {1+ \ alfa}}: \ y ^ {\ Frac {1} {1+ \ alfa}}}$${\ Displaystyle (x, y) \ w \ mathbb {R} _ {+} ^ {2}}$${\ Displaystyle \ textstyle \ Delta _ {\ alfa}}$${\displaystyle \textstyle T_{s,t}}$${\ Displaystyle \ textstyle s ^ {\ alfa} + t ^ {\ alfa} = 1}$

${\ Displaystyle x ^ {\ Frac {\ alfa} {\ alfa +1}} + Y ^ {\ Frac {\ alfa} {\ alfa +1}} <1.}$

Ponadto granicą zbioru jest obwiednia odpowiedniej rodziny odcinków linii ${\ Displaystyle \ mathbb {R} _ {+} ^ {2}}$${\ Displaystyle \ textstyle \ Delta _ {\ alfa}}$

${\ Displaystyle \ lewo \ {(x, y) \ w \ mathbb {R} _ {+} ^ {2}: \ {\ Frac {x} {s}} + {\ Frac {y} {t}} =1\right\}\ ,\qquad s^{\alpha }+t^{\alpha }=1}$

(czyli przeciwprostokątne trójkątów) i ma równanie kartezjańskie

${\ Displaystyle x ^ {\ Frac {\ alfa} {\ alfa +1}} + Y ^ {\ Frac {\ alfa} {\ alfa +1}} = 1.}$

Zauważ, że w szczególności wartość ta daje łuk paraboli z Przykładu 2 , a wartość (co oznacza, że ​​wszystkie przeciwprostokątne są segmentami o jednostkowej długości) daje astroidę . ${\ Displaystyle \ alfa =1}$${\ Displaystyle \ alfa = 2}$

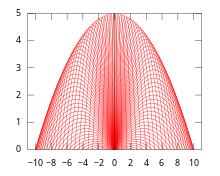
Przykład 5

Rozważamy następujący przykład koperty w ruchu. Załóżmy, że na wysokości początkowej 0 rzuca się pocisk w powietrze ze stałą prędkością początkową v, ale różnymi kątami elewacji θ. Niech x będzie osią poziomą na powierzchni ruchu, a y oznacza oś pionową. Wtedy ruch daje następujący różniczkowy układ dynamiczny :

${\ Displaystyle {\ Frac {d ^ {2} r} {dt ^ {2}}} = -g \; {\ Frac {d ^ {2} x} {dt ^ {2}}} = 0, }$

który spełnia cztery warunki początkowe :

${\ Displaystyle {\ Frac {dx} {dt}} {\ duży |} _ {t = 0} = v \ cos \ theta \; {\ Frac {dy} {dt}} {\ duży |} _ { t=0}=v\sin \theta ,\;x{\bigg |}_{t=0}=y{\bigg |}_{t=0}=0.}$

Tutaj t oznacza czas ruchu, θ oznacza kąt podniesienia, g oznacza przyspieszenie ziemskie , a v oznacza stałą prędkość początkową (nie prędkość ). Rozwiązanie powyższego systemu może przybrać formę niejawną :

${\ Displaystyle F (x, y, \ theta) = x \ tan \ theta - {\ Frac {gx ^ {2}} {2 v ^ {2} \ cos ^ {2} \ teta}} - y = 0. }$

Aby znaleźć jego równanie obwiedni, można obliczyć pożądaną pochodną:

${\ Displaystyle {\ Frac {\ częściowy F} {\ częściowy \ theta}} = {\ Frac {x} {\ cos ^ {2} \ theta}} - {\ Frac {gx ^ {2} \ tan \ teta }{v^{2}\cos ^{2}\theta }}=0.}$

Eliminując θ, można uzyskać następujące równanie obwiedni:

${\ Displaystyle y = {\ Frac {v ^ {2}} {2 g}} - {\ Frac {g} {2 v ^ {2}}} x ^ {2}.}$

Oczywiście uzyskana otoczka jest również wklęsłą parabolą .

Koperta rodziny powierzchni

Rodziny jeden parametr powierzchni w trójwymiarowej przestrzeni euklidesowej jest przez zestaw równań

${\ Displaystyle F (x, y, z, a) = 0}$

w zależności od rzeczywistego parametru a . Na przykład, płaszczyzny styczne do powierzchni wzdłuż krzywej na powierzchni tworzą taką rodzinę.

Dwie powierzchnie odpowiadające różnym wartościom a i a' przecinają się we wspólnej krzywej określonej przez

${\ Displaystyle F (x, y, z, a) = 0, \, \, {F (x, y, z, a ^ {\ prime}) - F (x, y, z, a) \ nad ^{\prim }-a}=0.}$

W granicy, gdy a' zbliża się do a , ta krzywa zmierza do krzywej zawartej w powierzchni w a

${\ Displaystyle F (x, y, z, a) = 0, \, \, {\ częściowy F \ nad \ częściowy a} (x, y, z, a) = 0.}$

Ta krzywa jest nazywana charakterystyką rodziny o . Ponieważ a zmienia się, miejsce tych charakterystycznych krzywych określa powierzchnię zwaną obwiednią rodziny powierzchni.

Obwiednia rodziny powierzchni jest styczna do każdej powierzchni w rodzinie wzdłuż krzywej charakterystycznej tej powierzchni.

Uogólnienia

Idea koperty z rodziny gładkich podrozmaitości następuje naturalnie. Ogólnie rzecz biorąc, jeśli mamy rodzinę podrozmaitości o kowymiarze c, to musimy mieć przynajmniej c -parametryczną rodzinę takich podrozmaitości. Na przykład: jednoparametrowa rodzina krzywych w trzech przestrzeniach ( c = 2) ogólnie nie ma obwiedni.

Aplikacje

Równania różniczkowe zwyczajne

Koperty są związane z badaniem równań różniczkowych zwyczajnych (ODE), aw szczególności rozwiązań osobliwych ODE. Rozważmy na przykład jednoparametrową rodzinę linii stycznych do paraboli y = x ² . Są one dane przez rodzinę generującą F ( t ,( x , y )) = t ² – 2 tx + y . Zestaw poziomu zerowego F ( t ₀ , ( x , y )) = 0 daje równanie linii stycznej do paraboli w punkcie ( t ₀ , t ₀ ² ). Równanie t ² – 2 tx + y = 0 można zawsze rozwiązać dla y w funkcji x, więc rozważmy

${\ Displaystyle t ^ {2} -2tx + y (x) = 0. \ }$

Zastępowanie

${\ Displaystyle t = \ lewo ({\ Frac {dy} {dx}} \ po prawej)/2}$

daje ODE

${\ Displaystyle \ lewo ({\ Frac {dy} {dx}} \ po prawej) ^ {2} \! \! 4x {\ Frac {dy} {dx}} + 4y = 0.}$

Nic dziwnego, że y  = 2 tx  −  t ² to wszystkie rozwiązania tego ODE. Jednak obwiednia tej jednoparametrowej rodziny linii, którą jest parabola y  =  x ² , jest również rozwiązaniem tego ODE. Innym znanym przykładem jest równanie Clairauta .

Równania różniczkowe cząstkowe

Obwiednie można wykorzystać do konstruowania bardziej skomplikowanych rozwiązań równań różniczkowych cząstkowych pierwszego rzędu (PDE) z prostszych. Niech F ( x , u , D U ) = 0 jest pierwszy PDE porządek, w którym x jest zmienna o wartości w zbiorze otwartym Ω ⊂  R ⁿ , u oznacza brak funkcji o wartościach rzeczywistych, D U jest gradientu od U , a F jest ciągle różniczkowalną funkcją, która jest regularna w Du . Załóżmy, że u ( x ; a ) jest m- parametrową rodziną rozwiązań: to znaczy dla każdego ustalonego a  ∈  A  ⊂  R ^m , u ( x ; a ) jest rozwiązaniem równania różniczkowego. Nowe rozwiązanie równania różniczkowego można skonstruować przez pierwsze rozwiązanie (jeśli to możliwe)

${\ Displaystyle D_ {a} u (x; a) = 0 \,}$

dla a  = φ( x ) jako funkcja x . Obwiednia rodziny funkcji { u (·, a )} _{a ∈ A} jest zdefiniowana przez

${\ Displaystyle v (x) = u (x; \ varphi (x)), \ quad x \ w \ Omega,}$

a także rozwiązuje równanie różniczkowe (pod warunkiem, że istnieje jako funkcja ciągle różniczkowalna).

Geometrycznie wykres v ( x ) jest wszędzie styczny do wykresu jakiegoś członka rodziny u ( x ; a ). Ponieważ równanie różniczkowe jest pierwszego rzędu, stawia warunek tylko na płaszczyźnie stycznej do wykresu, tak że każda funkcja wszędzie styczna do rozwiązania również musi być rozwiązaniem. Ta sama idea leży u podstaw rozwiązania równania pierwszego rzędu jako całki stożka Monge'a . Stożek Monge pole stożek w R ^{n + 1} z ( x , u ), zmienne wycięte obwiedni przestrzeni styczna do pierwszego rzędu PDE w każdym punkcie. Rozwiązaniem PDE jest wtedy obwiednia pola stożka.

W geometrii riemannowskiej , jeśli gładka rodzina geodezji przechodząca przez punkt P w rozmaitości riemannowskiej ma obwiednię, to P ma sprzężony punkt, w którym dowolna geodezja z rodziny przecina obwiednię. To samo dotyczy bardziej ogólnie rachunku wariacyjnego : jeśli rodzina ekstremów z funkcjonałem przechodzącym przez dany punkt P ma obwiednię, to punkt, w którym ekstremum przecina obwiednię, jest sprzężonym punktem z P .

Kaustyka

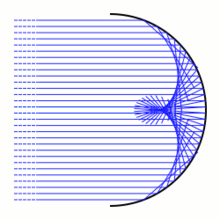
W optyki geometrycznej , A ługu jest koperta z rodziny promieni świetlnych . Na tym zdjęciu jest łuk koła. Promienie świetlne (pokazane na niebiesko) pochodzą ze źródła w nieskończoności , a więc docierają równolegle. Kiedy uderzają w kołowy łuk, promienie światła są rozpraszane w różnych kierunkach zgodnie z prawem odbicia . Kiedy promień światła uderza w łuk w pewnym punkcie, światło zostanie odbite tak, jakby zostało odbite od linii stycznej łuku w tym punkcie. Odbite promienie świetlne dają jednoparametrową rodzinę linii w płaszczyźnie. Otoczka tych linii to refleksyjna kaustyka . Odblaskowy środek kaustyczny będzie generalnie składał się z gładkich punktów i zwykłych punktów wierzchołkowych .

Z punktu widzenia rachunku wariacyjnego zasada Fermata (w swojej współczesnej postaci) sugeruje, że promienie świetlne są ekstremami dla funkcjonału długości

${\ Displaystyle L [\ gamma] = \ int _ {a} ^ {b} | \ gamma „(t) | \ dt}$

wśród gładkich krzywych γ na [ a , b ] ze stałymi punktami końcowymi γ( a ) i γ( b ). Kaustyka wyznaczona przez dany punkt P (na rysunku punkt jest w nieskończoności) jest zbiorem punktów sprzężonych do P .

Zasada Huygensa

Światło może przechodzić przez anizotropowe niejednorodne ośrodki z różną szybkością, w zależności od kierunku i początkowej pozycji promienia świetlnego. Granica zbioru punktów, do których światło może podróżować z danego punktu q po czasie t jest znana jako czoło fali po czasie t , oznaczane tutaj przez Φ _q ( t ). Składa się dokładnie z punktów, które można osiągnąć od q w czasie t , podróżując z prędkością światła. Zasada Huygensa zakłada, że ​​zbiór frontów fal Φ _{q 0} ( s + t ) jest obwiednią rodziny frontów fal Φ _q ( s ) dla q  ∈ Φ _{q 0} ( t ). Mówiąc bardziej ogólnie, punkt q ₀ można zastąpić dowolną krzywą, powierzchnią lub zbiorem zamkniętym w przestrzeni.

Zobacz też

• Rządzona powierzchnia
• Kaustyka (matematyka)

Bibliografia

Linki zewnętrzne

• Weisstein, Eric W. „Koperta” . MatematykaŚwiat .
• „Obwiednia rodziny krzywych płaskich” w MathCurve.