Wykres Eulera -Euler diagram

Ten artykuł dotyczy kręgów Eulera teorii mnogości i logiki. Aby zapoznać się z geometrycznym okręgiem Eulera, zobacz Okrąg dziewięciopunktowy .
Schemat Eulera ilustrujący, że zbiór „zwierząt z czterema nogami” jest podzbiorem „zwierząt”, ale zbiór „minerałów” jest rozłączny (nie ma wspólnych elementów) ze „zwierzętami”
Diagram Eulera pokazujący relacje między różnymi obiektami Układu Słonecznego

Diagram Eulera ( / ˈ ɔɪ l ər / , OY -lər ) jest diagramowym sposobem przedstawiania zbiorów i ich relacji. Są one szczególnie przydatne do wyjaśniania złożonych hierarchii i nakładających się definicji. Są one podobne do innej techniki tworzenia diagramów zbiorów, diagramów Venna . W przeciwieństwie do diagramów Venna, które pokazują wszystkie możliwe relacje między różnymi zestawami, diagram Eulera pokazuje tylko istotne relacje.

Pierwsze użycie „kręgów Eulera” powszechnie przypisuje się szwajcarskiemu matematykowi Leonhardowi Eulerowi (1707-1783). W Stanach Zjednoczonych zarówno diagramy Venna, jak i Eulera zostały włączone jako część instrukcji w teorii mnogości jako część nowego ruchu matematycznego z lat sześćdziesiątych. Od tego czasu zostały one również przyjęte przez inne dziedziny programu nauczania, takie jak czytanie, a także organizacje i firmy.

Diagramy Eulera składają się z prostych zamkniętych kształtów w dwuwymiarowej płaszczyźnie, z których każdy przedstawia zestaw lub kategorię. Jak lub czy te kształty się nakładają, pokazuje relacje między zestawami. Każda krzywa dzieli płaszczyznę na dwa regiony lub „strefy”: wnętrze, które symbolicznie reprezentuje elementy zbioru, i zewnętrze, które reprezentuje wszystkie elementy, które nie są członkami zbioru. Krzywe, które się nie nakładają, reprezentują zbiory rozłączne , które nie mają wspólnych elementów. Dwie nakładające się krzywe reprezentują zbiory, które się przecinają , które mają wspólne elementy; strefa wewnątrz obu krzywych reprezentuje zbiór elementów wspólnych dla obu zbiorów ( przecięcie zbiorów). Krzywa całkowicie wewnątrz innej jest jej podzbiorem .

Diagramy Venna są bardziej restrykcyjną formą diagramów Eulera. Diagram Venna musi zawierać wszystkie 2 n logicznie możliwe strefy nakładania się między jego n krzywymi, reprezentującymi wszystkie kombinacje włączenia/wyłączenia jego zbiorów składowych. Regiony niebędące częścią zbioru są oznaczone kolorem czarnym, w przeciwieństwie do diagramów Eulera, gdzie przynależność do zbioru jest wskazywana przez nakładanie się oraz kolor.

Historia

Strona z wykładów Hamiltona z logiki . Symbolika A, E, I i O odnosi się do zdań kategorycznych, które mogą wystąpić w sylogizmie . Mały tekst z lewej strony błędnie stwierdza: „Pierwsze zastosowanie diagramów kołowych w logice niewłaściwie przypisane Eulerowi. Można je znaleźć w Christian Weise”, książce faktycznie napisanej przez Johanna Christiana Lange.
Po prawej stronie znajduje się strona 74 z Couturat 1914, na której opisuje 8 regionów diagramu Venna. Współczesna nazwa tych „regionów” to minterms . Są one pokazane po lewej stronie ze zmiennymi x, y i z na rysunku Venna. Symbolika jest następująca: logiczne AND ( & ) jest reprezentowane przez mnożenie arytmetyczne, a logiczne NIE ( ~ ) jest reprezentowane przez " ' " po zmiennej, np. obszar x'y'z jest odczytywany jako "NIE x AND NIE y AND z" tj. ~x & ~y & z.
Zarówno diagram Veitcha, jak i mapa Karnaugha pokazują wszystkie mintermy , ale Veitch nie jest szczególnie przydatny do redukcji formuł. Zwróć uwagę na silne podobieństwo między diagramami Venna i Karnaugha; kolory i zmienne x, y i z są na przykładzie Venna.

Jak pokazano na ilustracji po prawej, Sir William Hamilton w swoich pośmiertnie opublikowanych Wykładach z metafizyki i logiki (1858–60) błędnie twierdzi, że pierwotne użycie kół do „zmysłowości… abstrakcji logiki” (s. 180) nie był Leonhardem Paulem Eulerem (1707–1783), ale raczej Christianem Weise (1642–1708) w jego Nucleus Logicae Weisianae , które ukazało się pośmiertnie w 1712 roku, jednak ta ostatnia książka została napisana przez Johanna Christiana Lange, a nie Weise. Odwołuje się do listów Eulera do niemieckiej księżniczki [Partie II, Lettre XXXV, 17 lutego 1791, wyd. Cournot (1842), s. 412-417. – wyd.]

Na ilustracji Hamiltona cztery zdania kategoryczne , które mogą wystąpić w sylogizmie , co symbolizują rysunki A, E, I i O to:

  • O: Uniwersalne potwierdzenie , Przykład: „Wszystkie metale są elementami”.
  • E: Uniwersalny Negatywny Przykład: „Żadne metale nie są substancjami złożonymi”.
  • I: Szczególne twierdzenie , Przykład: „Niektóre metale są kruche”.
  • O: Szczególny Negatywny Przykład: „Niektóre metale nie są kruche”.

W swoim 1881 Symbolic Logic Chapter V „Diagrammatic Representation” John Venn (1834-1923) komentuje niezwykłe rozpowszechnienie diagramu Eulera:

„… z pierwszych sześćdziesięciu traktatów logicznych, opublikowanych w ciągu ostatniego stulecia, z którymi konsultowano się w tym celu: – trochę przypadkowo, ponieważ były one najbardziej dostępne: – okazało się, że trzydzieści cztery apelowały o pomoc diagramy, z których prawie wszystkie wykorzystują schemat Eulera”. (Przypis 1, strona 100)
Złożony z dwóch stron 115-116 z Venn 1881 pokazujący jego przykład, jak przekształcić sylogizm trzech części w jego typ diagramu. Venn nazywa kręgi „kołami Eulera” (por. Sandifer 2003, Venn 1881:114 itd.) w „schemacie Eulera” (Venn 1881:100) „staromodnych diagramów Eulera” (Venn 1881:113).

Niemniej jednak, twierdził, „niestosowalność tego schematu do celów naprawdę ogólnej logiki” (str. 100) i na str. 101 zauważył, że „pasuje on, ale źle, nawet do czterech twierdzeń wspólnej logiki, do której jest normalnie stosowany." Venn kończy swój rozdział obserwacją zilustrowaną w poniższych przykładach – że ich użycie opiera się na praktyce i intuicji, a nie na ścisłej praktyce algorytmicznej :

„W rzeczywistości… te diagramy nie tylko nie pasują do zwykłego schematu zdań, które służą do zilustrowania, ale wydają się nie mieć żadnego uznanego schematu zdań, z którym mogłyby być konsekwentnie powiązane”. (s. 124–125)

Wreszcie, w Rozdziale XX NOTATKI HISTORYCZNE Venn przechodzi do krytycznej krytyki (zaznaczonej kursywą w poniższym cytacie); na ilustracji Hamiltona zaobserwuj, że O ( Szczególna negatywność ) i I ( Szczególna twierdząca ) są po prostu obrócone:

„Przechodzimy teraz do znanych kręgów Eulera, które po raz pierwszy zostały opisane w jego Lettres a une Princesse d'Allemagne (Listy 102–105). Słabym punktem w nich jest to, że ilustrują one tylko w ścisłym stosunku rzeczywiste relacje klas aniżeli niedoskonałą wiedzę o tych stosunkach, którą możemy posiadać lub chcieć przekazać za pomocą zdania.W związku z tym nie będą one pasować do twierdzeń logiki potocznej, lecz domagają się ukonstytuowania się nowej grupy odpowiednie zdania elementarne.... Wada ta musiała być zauważona od początku w przypadku poszczególnego twierdzącego i przeczącego, gdyż ten sam diagram jest powszechnie używany dla ich obu, co robi obojętnie dobrze ”. (dodana kursywa: strona 424)

(Sandifer 2003 donosi, że Euler również dokonuje takich obserwacji; Euler donosi, że jego figura 45 (proste przecięcie dwóch okręgów) ma 4 różne interpretacje). W każdym razie, uzbrojony w te obserwacje i krytykę, Venn następnie demonstruje (str. 100–125), w jaki sposób wyprowadził to, co stało się znane jako jego diagramy Venna , z „… staromodnych diagramów Eulera”. W szczególności podaje przykład pokazany po lewej stronie.

W 1914 Louis Couturat (1868-1914) oznaczył terminy tak, jak pokazano na rysunku po prawej stronie. Co więcej, oznaczył również obszar zewnętrzny (pokazany jako „b”c”). Zwięźle wyjaśnia, jak korzystać z diagramu – należy wykreślić obszary, które mają zniknąć:

„Metoda VENNA jest tłumaczona na diagramy geometryczne, które reprezentują wszystkie składniki, tak że aby uzyskać wynik, wystarczy wykreślić (poprzez zacieniowanie) te, które znikają z powodu danych problemu”. (kursywa dodana s. 73)

Biorąc pod uwagę zadania Venna, niezacienione obszary wewnątrz kół można zsumować, aby uzyskać następujące równanie dla przykładu Venna:

„Żadne Y to Z, a WSZYSTKIE X to Y: zatem żadne X to Z” ma równanie x'yz' + xyz' + x'y'z dla niezacienionego obszaru wewnątrz okręgów (ale to nie jest całkowicie poprawne; patrz następny akapit).

U Venna zerowy wyraz, x'y'z', tj. tło otaczające koła, nie występuje. Nigdzie nie jest to omawiane ani etykietowane, ale Couturat poprawia to na swoim rysunku. Prawidłowe równanie musi zawierać ten niezacieniony obszar pokazany pogrubioną czcionką:

„Żadne Y to Z, a WSZYSTKIE X to Y: zatem żadne X to Z” ma równanie x'yz' + xyz' + x'y'z + x'y'z' .

We współczesnym użyciu diagram Venna zawiera „pudełko”, które otacza wszystkie kręgi; nazywa się to wszechświatem dyskursu lub domeną dyskursu .

Couturat zauważa teraz, że w sposób bezpośredni algorytmiczny (formalny, systematyczny) nie można wyprowadzić zredukowanych równań Boole'a, ani nie pokazuje, jak dojść do wniosku „Nie X to Z”. Couturat stwierdził, że proces „ma… poważne niedogodności jako metoda rozwiązywania problemów logicznych”:

„Nie pokazuje, w jaki sposób dane są przedstawiane przez anulowanie niektórych składników, ani nie pokazuje, jak połączyć pozostałe składniki, aby uzyskać oczekiwane konsekwencje. Krótko mówiąc, służy tylko do wykazania jednego pojedynczego kroku w argumentacji, a mianowicie równania problemu; nie rezygnuje ani z poprzednich kroków, tj. „wrzucenia problemu w równanie” i przekształcenia przesłanek, ani z kolejnych kroków, tj. kombinacji, które prowadzą do różnych konsekwencji. jest bardzo mało użyteczny, ponieważ składowe mogą być reprezentowane przez symbole algebraiczne równie dobrze jak regiony płaskie i są znacznie łatwiejsze do czynienia w tej formie” (s. 75).

Tak więc sprawa pozostała aż do 1952 roku, kiedy Maurice Karnaugh (1924-) zaadaptował i rozszerzył metodę zaproponowaną przez Edwarda W. Veitcha ; praca ta opierałaby się na metodzie tabeli prawdy precyzyjnie zdefiniowanej w rozprawie doktorskiej Emila Posta z 1921 r. „Wstęp do ogólnej teorii zdań elementarnych” oraz zastosowaniu logiki zdań do logiki przełączania przez m.in. Claude’a Shannona , George’a Stibitza i Alana Turinga . Na przykład, w rozdziale "Algebra Boole'a", Hill i Peterson (1968, 1964) prezentują sekcje 4.5ff "Teoria mnogości jako przykład algebry Boole'a", a w niej przedstawiają diagram Venna z cieniowaniem i wszystkim. Podają przykłady diagramów Venna, aby rozwiązać przykładowe problemy z obwodami przełączającymi, ale kończą z następującym stwierdzeniem:

„Dla więcej niż trzech zmiennych podstawowa ilustracyjna forma diagramu Venna jest niewystarczająca. Możliwe są rozszerzenia, jednak najwygodniejszą z nich jest mapa Karnaugha, o której będzie mowa w rozdziale 6.”. (str. 64)

W rozdziale 6, sekcja 6.4 „Reprezentacja funkcji logicznych w mapie Karnaugha” zaczynają się od:

„Mapa Karnaugh 1 [ 1 Karnaugh 1953] jest jednym z najpotężniejszych narzędzi w repertuarze projektanta logiki. ... Mapa Karnaugha może być traktowana albo jako obrazowa forma tabeli prawdy, albo jako rozszerzenie Venna diagram." (s. 103-104)

Historia rozwoju jego metody „wykresu” lub „mapy” przez Karnaugha jest niejasna. Karnaugh w swojej pracy z 1953 odwoływał się do Veitcha 1951, Veitch odwoływał się do Claude'a E. Shannona 1938 (zasadniczo praca magisterska Shannona na MIT ), a Shannon z kolei odwoływał się, między innymi do autorów tekstów logicznych, do Couturata 1914. W metodzie Veitcha zmienne są ułożone w prostokąt lub kwadratowy; jak opisano w Karnaugh map , Karnaugh w swojej metodzie zmienił kolejność zmiennych, aby odpowiadała temu, co stało się znane jako (wierzchołki) hipersześcianu .

Związek między diagramami Eulera i Venna

Przykłady małych diagramów Venna (po lewej) z zacienionymi obszarami reprezentującymi puste zbiory , pokazujące jak można je łatwo przekształcić w równoważne diagramy Eulera (po prawej)

Diagramy Venna są bardziej restrykcyjną formą diagramów Eulera. Diagram Venna musi zawierać wszystkie 2 n logicznie możliwe strefy nakładania się między jego n krzywymi, reprezentującymi wszystkie kombinacje włączenia/wyłączenia jego zbiorów składowych. Regiony niebędące częścią zbioru są oznaczone kolorem czarnym, w przeciwieństwie do diagramów Eulera, gdzie przynależność do zbioru jest wskazywana przez nakładanie się oraz kolor. Gdy liczba zestawów rośnie powyżej 3, diagram Venna staje się wizualnie złożony, zwłaszcza w porównaniu z odpowiednim diagramem Eulera. Różnicę między diagramami Eulera i Venna można zobaczyć w poniższym przykładzie. Weź trzy zestawy:

Diagramy Eulera i Venna tych zbiorów to:

  • Wykres Eulera

    Wykres Eulera

  • Schemat Venna

    Schemat Venna

W warunkach logicznych można użyć semantyki teorii modeli do interpretacji diagramów Eulera w obrębie uniwersum dyskursu . W poniższych przykładach diagram Eulera pokazuje, że zbiory Animal i Mineral są rozłączne, ponieważ odpowiadające im krzywe są rozłączne, a także, że zbiór Four Legs jest podzbiorem zbioru Animal s. Diagram Venna, który wykorzystuje te same kategorie Animal , Mineral i Four Legs , nie obejmuje tych zależności. Tradycyjnie pustkę zbioru na diagramach Venna przedstawia się za pomocą cieniowania w regionie. Diagramy Eulera przedstawiają pustkę przez cieniowanie lub brak regionu.

Często narzucany jest zestaw dobrze uformowanych warunków; są to ograniczenia topologiczne lub geometryczne nałożone na strukturę diagramu. Na przykład połączenie stref może być wymuszane lub współbieżność krzywych lub wiele punktów może być zabroniona, podobnie jak styczne przecięcie krzywych. Na sąsiednim diagramie przykłady małych diagramów Venna są przekształcane w diagramy Eulera przez sekwencje przekształceń; niektóre z diagramów pośrednich mają współbieżność krzywych. Jednak tego rodzaju przekształcenie diagramu Venna z cieniowaniem na diagram Eulera bez cieniowania nie zawsze jest możliwe. Istnieją przykłady diagramów Eulera z 9 zestawami, których nie można narysować za pomocą prostych krzywych zamkniętych bez tworzenia niepożądanych stref, ponieważ musiałyby mieć nieplanarne grafy dualne.

Przykład: diagram Eulera do Venna i mapa Karnaugh

Ten przykład pokazuje diagramy Eulera i Venna oraz mapę Karnaugha wyprowadzającą i weryfikującą dedukcję „Brak X s to Z s”. Na ilustracji i w tabeli zastosowano następujące symbole logiczne:

  • 1 można odczytać jako „prawda”, 0 jako „fałsz”
  • ~ for NOT i skrócone do ' podczas ilustrowania mintermów, np. x' = zdefiniowane NOT x,
  • + dla Boole'a OR (z algebry Boole'a : 0 + 0 = 0, 0 + 1 = 1 + 0 = 1, 1 + 1 = 1)
  • & (logiczne AND) między zdaniami; w mintermach AND jest pomijane w sposób podobny do mnożenia arytmetycznego: np. x'y'z = zdefiniowane ~x & ~y & z (z algebry Boole'a: 0.0 = 0, 0.1 = 1.0 = 0, 1.1 = 1, gdzie „·” jest pokazane dla jasności)
  • → (IMPLIKACJE logiczne): czytaj jako JEŻELI ... TO ..., lub "IMPLIKA", P → Q =  zdefiniowane NIE P OR Q
Zanim będzie można go przedstawić na diagramie Venna lub mapie Karnaugha, sylogizm diagramu Eulera „Nie Y to Z , All X to Y ” musi zostać najpierw przeredagowany na bardziej formalny język rachunku zdań : „Nie jest tak, że : Y AND Z' ORAZ 'Jeżeli X , to Y' ". Gdy zdania zostaną zredukowane do symboli i formuły zdań ( ~(y & z) & (x → y) ), można skonstruować tablicę prawdy formuły ; z tej tabeli można łatwo utworzyć mapę Venna i/lub Karnaugha. Używając sąsiedztwa „1” na mapie Karnaugha (wskazanego przez szare owale wokół wyrazów 0 i 1 oraz wokół wyrazów 2 i 6) można „zredukować” przykładowe równanie logiczne, tj. (x'y'z' + x'y'z) + (x'yz' + xyz') do zaledwie dwóch wyrazów: x'y' + yz'. Ale środki do wydedukowania pojęcia, że ​​"żadne X nie jest Z" i jak ta redukcja odnosi się do tej dedukcji, nie pochodzi z tego przykładu.

Biorąc pod uwagę proponowany wniosek, taki jak „Nie X to Z ”, można sprawdzić, czy jest to poprawna dedukcja , używając tabeli prawdy . Najprostszą metodą jest umieszczenie początkowej formuły po lewej stronie (w skrócie P ) a po prawej stronie (możliwej) dedukcji (w skrócie Q ) i połączeniu tych dwóch z logiczną implikacją tj . P → Q , czytane jako JEŻELI P TO P . Jeśli ocena tablicy prawdy daje wszystkie jedynki pod znakiem implikacji (→, tzw. spójnik główny ), to P → Q jest tautologią . Biorąc pod uwagę ten fakt, można „odłączyć” formułę po prawej stronie (w skrócie Q ) w sposób opisany poniżej tabeli prawdy.

Biorąc pod uwagę powyższy przykład, wzór na diagramy Eulera i Venna to:

„Nie Y s to Z s” i „Wszystkie X s to Y s”: ( ~(y & z) & (x → y) ) = określone P

A proponowana odliczenie to:

„Żadne X s to Z s”: ( ~ (x & z)) = zdefiniowany Q

Więc teraz formuła do oceny może być skrócona do:

( ~ (y & z) & (x → y) ) → ( ~ (x & z) ): P → Q
IF („Brak Y to Z ” i „Wszystkie X to Y ”) THEN („Brak X to Z ”)
Tabela Prawdy pokazuje, że formuła ( ~(y & z) & (x → y)) → ( ~ (x & z)) jest tautologią, jak pokazują wszystkie jedynki w żółtej kolumnie.
Kwadrat # Venn, region Karnaugh x tak z (~ (y & z) & (x → y)) → (~ (x & z))
0 x'y'z'   0 0 0   1 0 0 0 1 0 1 0 1 1 0 0 0
1 x'y'z   0 0 1   1 0 0 1 1 0 1 0 1 1 0 0 1
2 x'yz'   0 1 0   1 1 0 0 1 0 1 1 1 1 0 0 0
3 x'yz   0 1 1   0 1 1 1 0 0 1 1 1 1 0 0 1
4 xy'z'   1 0 0   1 0 0 0 0 1 0 0 1 1 1 0 0
5 xy'z   1 0 1   1 0 0 1 0 1 0 0 1 0 1 1 1
6 xyz”   1 1 0   1 1 0 0 1 1 1 1 1 1 1 0 0
7 xyz   1 1 1   0 1 1 1 0 1 1 1 1 0 1 1 1

W tym momencie powyższa implikacja P → Q (tj. ~(y & z) & (x → y) ) → ~(x & z) ) jest nadal wzorem, a dedukcja – „oderwanie” Q od P → Q – nie wystąpił. Ale biorąc pod uwagę wykazanie, że P → Q jest tautologią, przygotowana jest teraz procedura modus ponens , aby „odłączyć” Q: „Żadne X nie są Z ” i zrezygnować z określeń po lewej stronie.

Modus ponens (lub „podstawowa zasada wnioskowania”) jest często zapisywana w następujący sposób: Dwa terminy po lewej stronie, P → Q i P , nazywane są przesłankami (umownie połączone przecinkiem), symbol ⊢ oznacza „wydajność” (w sensie logicznej dedukcji), a termin po prawej nazywa się wnioskiem :

P → Q , P ⊢ Q

Aby modus ponens się powiódł, obie przesłanki P → Q i P muszą być prawdziwe . Ponieważ, jak wykazano powyżej, założenie P → Q jest tautologią, „prawda” ma zawsze miejsce, niezależnie od wartości x, y i z, ale „prawda” ma znaczenie tylko dla P w tych okolicznościach, gdy P ocenia się jako „ prawda” (np. wiersze 0 LUB 1 LUB 2 LUB 6 : x'y'z' + x'y'z + x'yz' + xyz' = x'y' + yz').

P → Q , P ⊢ Q
  • tj.: ( ~(y & z) & (x → y) ) → ( ~ (x & z) ) , ( ~(y & z) & (x → y)) ) ⊢ ( ~ (x & z)) )
  • np.: JEŻELI „Nie Y to Z ” i „Wszystkie X to Y ” TO „Nie X to Z ”, „Nie Y to Z ” i „Wszystkie X to Y ” ⊢ „Nie X s to Z s"

Można teraz „odłączyć” wniosek „Żadne X nie są Z ”, być może, aby użyć go w późniejszej dedukcji (lub jako temat rozmowy).

Użycie implikacji tautologicznej oznacza, że ​​istnieją inne możliwe dedukcje oprócz „Żadne X nie są Z s”; kryterium pomyślnej dedukcji jest to, że jedynki pod spójnikiem podrzędnym po prawej stronie zawierają wszystkie jedynki pod spójnikiem podrzędnym po lewej stronie ( główny spójnik jest implikacją, która skutkuje tautologią). Na przykład, w tabeli prawdy, po prawej stronie implikacji (→, główny symbol spójnika) kolumna pogrubiona pod podrzędnym głównym symbolem spójnika „ ~ ” ma te same jedynki, które pojawiają się w licowana kolumna pod spójnikiem głównym po lewej stronie & (wiersze 0 , 1 , 2 i 6 ), plus jeszcze dwa (wiersze 3 i 4 ).

Galeria

Council of Europe Schengen Area European Free Trade Association European Economic Area Eurozone European Union European Union Customs Union Agreement with EU to mint euros GUAM Central European Free Trade Agreement Nordic Council Baltic Assembly Benelux Visegrád Group Common Travel Area Organization of the Black Sea Economic Cooperation Union State Switzerland Iceland Norway Liechtenstein Sweden Denmark Finland Poland Czech Republic Hungary Slovakia Greece Estonia Latvia Lithuania Belgium Netherlands Luxembourg Italy France Spain Austria Germany Portugal Slovenia Malta Cyprus Ireland United Kingdom Croatia Romania Bulgaria Turkey Monaco Andorra San Marino Vatican City Georgia Ukraine Azerbaijan Moldova Armenia Russia Belarus Serbia Albania North Macedonia Bosnia and Herzegovina Montenegro Kosovo (UNMIK)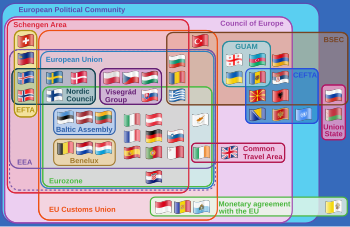Ponadnarodowe organy europejskie-en.svg
O tym obrazie
Klikalny diagram Eulera [plik] przedstawiający relacje między różnymi międzynarodowymi organizacjami europejskimi i umowami.
  • Diagram Venna pokazuje wszystkie możliwe skrzyżowania.

    Diagram Venna pokazuje wszystkie możliwe skrzyżowania.

  • Diagram Eulera wizualizujący rzeczywistą sytuację, relacje między różnymi ponadnarodowymi organizacjami europejskimi. (wersja klikalna)

    Diagram Eulera wizualizujący rzeczywistą sytuację, relacje między różnymi ponadnarodowymi organizacjami europejskimi . ( wersja klikalna )

  • Humorystyczny diagram porównujący diagramy Eulera i Venna.

    Humorystyczny diagram porównujący diagramy Eulera i Venna .

  • Schemat Eulera typów trójkątów, wykorzystujący definicję, że trójkąty równoramienne mają co najmniej (a nie dokładnie) 2 równe boki.

    Schemat Eulera typów trójkątów , wykorzystujący definicję, że trójkąty równoramienne mają co najmniej (a nie dokładnie) 2 równe boki.

  • Schemat Eulera terminologii Wysp Brytyjskich.

    Schemat Eulera terminologii Wysp Brytyjskich .

  • 22 (z 256) zasadniczo różne diagramy Venna z 3 okręgami (u góry) i odpowiadające im diagramy Eulera (na dole) Niektóre diagramy Eulera nie są typowe, a niektóre są nawet równoważne diagramom Venna. Obszary są zacienione, aby wskazać, że nie zawierają żadnych elementów.

    22 (z 256) zasadniczo różne diagramy Venna z 3 okręgami (u góry) i odpowiadające im diagramy Eulera (na dole)
    Niektóre diagramy Eulera nie są typowe, a niektóre są nawet równoważne diagramom Venna. Obszary są zacienione, aby wskazać, że nie zawierają żadnych elementów.

  • Henri Milne-Edwards (1844) diagram związków kręgowców, zilustrowany jako seria zagnieżdżonych zbiorów.

    Henri Milne-Edwards (1844) diagram związków kręgowców, zilustrowany jako seria zagnieżdżonych zbiorów.

Zobacz też

Uwagi

Bibliografia

Dalsza lektura

Według daty publikacji:

Zewnętrzne linki