Gradient — Gradient

Gradient, reprezentowany przez niebieskie strzałki, oznacza kierunek największej zmiany funkcji skalarnej. Wartości funkcji są reprezentowane w skali szarości i rosną od białego (niski) do ciemnego (wysoki).

W wektorze rachunku The gradientu z skalarnej wartościach funkcji różniczkowalną f od wielu zmiennych jest pole wektorowe (lub funkcja wektorowa ) , którego wartość w punkcie, jest wektor , których składniki są pochodnymi cząstkowymi z co . Czyli dla , jego gradient jest zdefiniowany w punkcie w przestrzeni n- wymiarowej jako wektor: ${\ Displaystyle \ nabla f}$${\displaystyle p}$${\displaystyle f}$${\displaystyle p}$${\ Displaystyle f \ dwukropek \ mathbb {R} ^ {n} \ do \ mathbb {R}}$${\ Displaystyle \ nabla f \ okrężnica \ mathbb {R} ^ {n} \ do \ mathbb {R} ^ {n}}$${\ Displaystyle p = (x_ {1}, \ ldots, x_ {n})}$

${\ Displaystyle \ nabla f (p) = {\ zacząć {bmatrix} {\ Frac {\ częściowy f} {\ częściowy x_ {1}}} (p) \ \ \ vdots \ \ {\ Frac {\ częściowy f} {\częściowy x_{n}}}(p)\end{bmatryca}}.}$

Symbolu nabla , zapisanych w postaci trójkąta odwróconej i nazywana „del” oznacza operator różnicowy wektor . ${\displaystyle \nabla}$

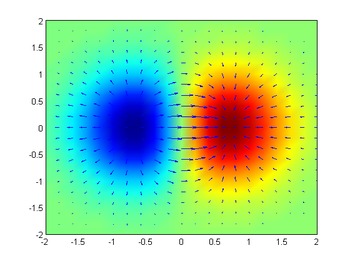
Wektor gradientu można interpretować jako „kierunek i tempo najszybszego wzrostu”. Jeżeli gradient funkcji jest niezerowy w punkcie p , kierunek gradientu jest kierunkiem, w którym funkcja rośnie najszybciej od p , a wielkość gradientu to tempo wzrostu w tym kierunku, największe bezwzględna pochodna kierunkowa. Ponadto gradient jest wektorem zerowym w punkcie wtedy i tylko wtedy, gdy jest to punkt stacjonarny (gdzie znika pochodna). Gradient odgrywa zatem fundamentalną rolę w teorii optymalizacji , gdzie jest używany do maksymalizacji funkcji przez wznoszenie gradientu .

Gradient jest podwójny do całkowitej pochodnej : wartość gradientu w punkcie jest wektorem stycznym – wektorem w każdym punkcie; natomiast wartością pochodnej w punkcie jest wektor co tangens – funkcja liniowa na wektorach. Są one związane z tym, że punkt produkt z gradientem F w punkcie P z innym styczna wektora V równa się kierunkowe pochodną o f w p funkcji wzdłuż v ; czyli . Gradient dopuszcza wiele uogólnień do bardziej ogólnych funkcji na rozmaitościach ; patrz § Uogólnienia . ${\displaystyle df}$${\textstyle \nabla f(p)\cdot \mathbf {v} ={\frac {\częściowy f}{\częściowy \mathbf {v} }}(p)=df_{\mathbf {v} }(p) }$

Motywacja

Gradient funkcji 2D f ( x , y ) = xe ^{−( x 2 + y 2 )} jest wykreślony jako niebieskie strzałki nad pseudokolorowym wykresem funkcji.

Rozważmy pomieszczenia, w którym temperatura jest podana przez skalarne dziedzinie , T , aby w każdym punkcie ( x , y , oo ) temperatura T ( x , y , z ) , niezależnie od czasu. W każdym punkcie pomieszczenia gradient T w tym punkcie pokaże kierunek, w którym temperatura rośnie najszybciej, oddalając się od ( x , y , z ) . Wielkość gradientu określi, jak szybko temperatura wzrasta w tym kierunku.

Rozważmy powierzchnię, której wysokość nad poziomem morza w punkcie ( x , y ) wynosi H ( x , y ) . Gradient H w punkcie jest wektorem płaskim wskazującym w kierunku najbardziej stromego nachylenia lub nachylenia w tym punkcie. Nachylenie zbocza w tym punkcie jest określone przez wielkość wektora gradientu.

Gradientu można również użyć do pomiaru zmian pola skalarnego w innych kierunkach, a nie tylko w kierunku największej zmiany, przyjmując iloczyn skalarny . Załóżmy, że najbardziej strome nachylenie na wzgórzu wynosi 40%. Droga prowadząca bezpośrednio pod górę ma nachylenie 40%, ale droga okrążająca wzgórze pod kątem będzie miała nachylenie płytsze. Na przykład, jeśli droga jest pod kątem 60° od kierunku pod górę (gdy oba kierunki są rzutowane na płaszczyznę poziomą), wówczas nachylenie wzdłuż drogi będzie iloczynem skalarnym między wektorem gradientu a wektorem jednostkowym wzdłuż drogi , czyli 40% razy cosinus 60°, czyli 20%.

Mówiąc ogólnie, jeśli funkcja wysokość wzgórza H jest różniczkowalną , następnie gradient H przerywana z wektor jednostkowy daje nachylenie Hill w kierunku wektorze kierunkowego pochodnej o H wzdłuż wektora jednostkowego.

Notacja

Gradient funkcji w punkcie jest zwykle zapisywany jako . Może być również oznaczony dowolnym z poniższych: ${\displaystyle f}$${\displaystyle a}$${\ Displaystyle \ nabla f (a)}$

• ${\displaystyle {\vec {\nabla}}f(a)}$ : aby podkreślić wektorowy charakter wyniku.
• grad f
• ${\ Displaystyle \ lewo. {\ Frac {\ częściowy f} {\ częściowy x}} \ prawo | _ {x = a}}$
• ${\ Displaystyle \ lewo. {\ Frac {\ częściowy f} {\ częściowy \ mathbf {x}}} \ prawo | _ {\ mathbf {x = a}}}$
• ${\ Displaystyle \ częściowe _ {i} f}$oraz  : notacja Einsteina .${\displaystyle f_{i}}$

Definicja

Gradient funkcji f ( x , y ) = −(cos ² x + cos ² y ) ² przedstawiony jako rzutowane pole wektorowe na dolną płaszczyznę.

Gradient (lub gradientowe pole wektorowe) funkcji skalarnej f ( x ₁ , x ₂ , x ₃ , …, x _n ) jest oznaczony ∇ f lub ∇ → f gdzie ∇ ( nabla ) oznacza wektorowy operator różniczkowy , del . Notacja grad f jest również powszechnie używana do reprezentowania gradientu. Gradient f jest zdefiniowany jako unikalne pole wektorowe, którego iloczyn skalarny z dowolnym wektorem v w każdym punkcie x jest pochodną kierunkową f wzdłuż v . To jest,

${\ Displaystyle {\ duży (} \ nabla f (x) {\ duży )} \ cdot \ mathbf {v} = D_ {\ mathbf {v}} f (x).}$

Formalnie gradient jest podwójny do pochodnej; zobacz związek z pochodną .

Gdy funkcja zależy również od parametru, takiego jak czas, gradient często odnosi się po prostu do wektora jej pochodnych przestrzennych (patrz Gradient przestrzenny ).

Wielkość i kierunek wektora gradientu są niezależne od reprezentacji poszczególnych współrzędnych .

współrzędne kartezjańskie

W trójwymiarowym kartezjańskim układzie współrzędnych z metryką euklidesową gradient, jeśli istnieje, jest określony wzorem:

${\ Displaystyle \ nabla f = {\ Frac {\ częściowy f} {\ częściowy x}} \ mathbf {i} + {\ Frac {\ częściowy f} {\ częściowy y}} \ mathbf {j} + {\ Frac {\częściowy f}{\częściowy z}}\mathbf {k} ,}$

gdzie i , j , k są standardowymi wektorami jednostkowymi w kierunkach odpowiednio x , y i z . Na przykład gradient funkcji

${\ Displaystyle f (x, y, z) = 2x + 3y ^ {2} - \ sin (z)}$

jest

${\ Displaystyle \ nabla f = 2 \ mathbf {i} + 6y \ mathbf {j} - \ cos (z) \ mathbf {k}}.$

W niektórych zastosowaniach zwyczajowo przedstawia się gradient jako wektor wierszowy lub wektor kolumnowy jego składowych w prostokątnym układzie współrzędnych; ten artykuł jest zgodny z konwencją gradientu będącego wektorem kolumnowym, podczas gdy pochodna jest wektorem wierszowym.

Współrzędne cylindryczne i sferyczne

We współrzędnych cylindrycznych z metryką euklidesową gradient wyraża się wzorem:

${\ Displaystyle \ nabla f (\ rho, \ varphi, z) = {\ Frac {\ częściowy f} {\ częściowy \ rho}} \ mathbf {e} _ {\ rho} + {\ Frac {1} {\ rho }}{\frac {\częściowy f}{\częściowy \varphi }}\mathbf {e} _{\varphi }+{\frac {\częściowy f}{\częściowy z}}\mathbf {e} _{ z},}$

gdzie ρ jest odległość osiowa φ jest azymutu i kąta azymutu, z jest współrzędną osiowe i e _ρ , e _φ i e _z wektory jednostki wskazujące wzdłuż współrzędnych kierunkach.

We współrzędnych sferycznych gradient wyraża się wzorem:

${\ Displaystyle \ nabla f (r \ theta \ varphi ) = {\ Frac {\ częściowy f} {\ częściowy r}} \ mathbf {e} _ {r} + {\ Frac {1} {r}} {\frac {\częściowy f}{\częściowy \theta }}\mathbf {e} _{\theta }+{\frac {1}{r\sin \theta }}{\frac {\częściowy f}{\ częściowe \varphi }}\mathbf {e} _{\varphi },}$

gdzie R oznacza odległość promieniową, φ jest kąt kierunkowy i θ jest kątowa i e _r , e _θ i e _φ znowu miejsca wektor jednostkowy zwróconą w kierunku koordynacji (to znaczy znormalizowana bazowych kowariantna ).

Aby zapoznać się z gradientem w innych ortogonalnych układach współrzędnych , zobacz Współrzędne ortogonalne (Operatory różniczkowe w trzech wymiarach) .

Współrzędne ogólne

Rozważamy współrzędne ogólne , które zapisujemy jako x ¹ , …, x ⁱ , …, x ⁿ , gdzie n jest liczbą wymiarów dziedziny. W tym przypadku górny indeks odnosi się do pozycji na liście współrzędnych lub składnika, więc x ² odnosi się do drugiego składnika, a nie do ilości x do kwadratu. Zmienna indeksująca i odnosi się do dowolnego elementu x ⁱ . Używając notacji Einsteina , gradient można następnie zapisać jako:

${\ Displaystyle \ nabla f = {\ Frac {\ częściowy f} {\ częściowy x ^ {i}}} g ^ {ij} \ mathbf {e} _ {j}}$ (Zauważ, że jego podwójna jest ),${\ Displaystyle \ operatorname {d} f = {\ Frac {\ częściowy f} {\ częściowy x ^ {i}}} \ mathbf {e} ^ {i}}$

gdzie i odnoszą się odpowiednio do nieznormalizowanych lokalnych zasad kowariantnych i kontrawariantnych , jest tensorem metryki odwrotnej , a konwencja sumowania Einsteina implikuje sumowanie przez i oraz j . ${\ Displaystyle \ mathbf {e} _ {i} = \ częściowy \ mathbf {x} / \ częściowy x ^ {i}}$${\ Displaystyle \ mathbf {e} ^ {i} = \ operatorname {d} x ^ {i}}$${\ Displaystyle g ^ {ij}}$

Jeśli współrzędne są ortogonalne, możemy łatwo wyrazić gradient (i różniczkę ) w postaci znormalizowanych baz, które nazywamy i , używając współczynników skali (znanych również jako współczynniki Lamé )  : ${\displaystyle {\kapelusz {\mathbf {e}}}_ {i}}$${\ Displaystyle {\ kapelusz {\ mathbf {e} }} ^ {i}}$${\ Displaystyle h_ {i} = \ lVert \ mathbf {e} _ {i} \ rVert = 1 \, / \ lVert \ mathbf {e} ^ {i} \ rVert}$

${\ Displaystyle \ nabla f = \ suma _ {i = 1} ^ {n} \ {\ Frac {\ częściowy f} {\ częściowy x ^ {i}}} {\ Frac {1} {h_ {i} }}\mathbf {\kapelusz {e}} _{i}}$ ( i ),${\ Displaystyle \ operatorname {d} f = \ suma _ {i = 1} ^ {n} \ {\ Frac {\ częściowy f} {\ częściowy x ^ {i}}} {\ Frac {1} {h_ {i}}}\mathbf {\kapelusz {e}} ^{i}}$

gdzie nie możemy użyć notacji Einsteina, ponieważ nie da się uniknąć powtórzenia więcej niż dwóch indeksów. Pomimo zastosowania górnych i dolnych indeksów , , i nie są ani kontrawariantne, ani kowariantne. ${\ Displaystyle \ mathbf {\ kapelusz {e}} _ {i}}$${\ Displaystyle \ mathbf {\ kapelusz {e}} ^ {i}}$${\displaystyle h_{i}}$

To ostatnie wyrażenie daje w wyniku wyrażenia podane powyżej dla współrzędnych cylindrycznych i sferycznych.

Związek z pochodną

Związek z całkowitą pochodną

Gradient jest ściśle powiązany z pochodną całkowitą ( różnicką całkowitą ) : są one transponowane ( podwójne ) do siebie. Stosując konwencję, że wektory w są reprezentowane przez wektory kolumnowe , a kowektory (mapy liniowe ) są reprezentowane przez wektory wierszowe , gradient i pochodna są wyrażane odpowiednio jako wektor kolumnowy i wierszowy, z tymi samymi składnikami, ale transponują każdy z nich inny: ${\displaystyle df}$${\ Displaystyle \ mathbb {R} ^ {n}}$${\ Displaystyle \ mathbb {R} ^ {n} \ do \ mathbb {R}}$${\ Displaystyle \ nabla f}$${\displaystyle df}$

${\ Displaystyle \ nabla f (p) = {\ zacząć {bmatrix} {\ Frac {\ częściowy f} {\ częściowy x_ {1}}} (p) \ \ \ vdots \ \ {\ Frac {\ częściowy f} {\częściowy x_{n}}}(p)\end{bmatryca}};}$

${\ Displaystyle df_ {p} = {\ zacząć {bmatrix} {\ Frac {\ częściowy f} {\ częściowy x_ {1}}} (p) i \ cdots i {\ Frac {\ częściowy f} {\ częściowy X_ {n}}}(p)\koniec{bmatrycy}}.}$

Chociaż oba mają te same składniki, różnią się rodzajem obiektu matematycznego, który reprezentują: w każdym punkcie pochodną jest wektor kostyczny , forma liniowa ( covector ), która wyraża, jak bardzo (skalarny) zmienia się wynik dla danej nieskończenie małej zmiana wejścia (wektorowego), podczas gdy w każdym punkcie gradient jest wektorem stycznym , który reprezentuje nieskończenie małą zmianę wejścia (wektorowego). W symbolach gradient jest elementem przestrzeni stycznej w punkcie , natomiast pochodna jest odwzorowaniem przestrzeni stycznej na liczby rzeczywiste , . Przestrzenie styczne w każdym punkcie można „naturalnie” utożsamić z samą przestrzenią wektorową i podobnie przestrzeń kostyczną w każdym punkcie można naturalnie utożsamić z podwójną przestrzenią wektorową kowektorów; w ten sposób wartość gradientu w punkcie można traktować jako wektor w oryginale , a nie tylko jako wektor styczny. ${\ Displaystyle \ nabla f (p) \ w T_ {p} \ mathbb {R} ^ {n}}$${\ Displaystyle df_ {p} \ dwukropek T_ {p} \ mathbb {R} ^ {n} \ do \ mathbb {R}}$${\ Displaystyle \ mathbb {R} ^ {n}}$${\ Displaystyle \ mathbb {R} ^ {n}}$ ${\ Displaystyle (\ mathbb {R} ^ {n}) ^ {*}}$${\ Displaystyle \ mathbb {R} ^ {n}}$

Obliczeniowo, mając wektor styczny, wektor można pomnożyć przez pochodną (jako macierze), co jest równe pobraniu iloczynu skalarnego z gradientem:

${\ Displaystyle (df_ {p}) (v) = {\ zacząć {bmatrix} {\ Frac {\ częściowy f} {\ częściowy x_ {1}}} (p) i \ cdots i {\ Frac {\ częściowy f }{\częściowa x_{n}}}(p)\end{bmacierz}}{\begin{bmacierz}v_{1}\\\vdots \\v_{n}\end{bmacierz}}=\sum _{ i=1}^{n}{\frac {\częściowy f}{\częściowy x_{i}}}(p)v_{i}={\begin{bmatrix}{\frac {\częściowy f}{\częściowy x_{1}}}(p)\\\vdots \\{\frac {\częściowy f}{\częściowy x_{n}}}(p)\end{bmacierz}}\cdot {\begin{bmacierz}v_ {1}\\\vdots \\v_{n}\end{bmatryca}}=\nabla f(p)\cdot v}$

Różniczka lub (zewnętrzna) pochodna

Najlepsze przybliżenie liniowe do funkcji różniczkowalnej

${\ Displaystyle f \ dwukropek \ mathbb {R} ^ {n} \ do \ mathbb {R}}$

w punkcie X, w R ⁿ jest liniowym z R ^N do B , który jest często oznaczany przez df _X lub Df ( x ) i zwany różnicowy lub całkowitą pochodną o f w x . Funkcja DF , który odwzorowuje x do DF _x jest nazywany całkowitej różnicy lub zewnętrzne pochodną o f i jest przykładem różnicowego 1-formy .

Podobnie jak pochodna funkcji jednej zmiennej oznacza nachylenie na stycznej do wykresu funkcji kierunkowa pochodną funkcją wielu zmiennych oznacza nachylenie stycznej hiperpłaszczyznę w kierunku wektora.

Gradient jest powiązany z różniczką wzorem

${\ Displaystyle (\ nabla f) _ {x} \ cdot v = df_ {x} (v)}$

dla dowolnego v ∈ R ⁿ , gdzie jest iloczynem skalarnym : pobranie iloczynu skalarnego wektora z gradientem jest takie samo, jak pobranie pochodnej kierunkowej wzdłuż wektora. ${\displaystyle \cdot}$

Jeżeli R ⁿ jest postrzegane jako przestrzeń (wymiar n ) wektorów kolumnowych (liczb rzeczywistych), to df można traktować jako wektor wierszowy ze składowymi

${\ Displaystyle \ lewo ({\ Frac {\ częściowy f} {\ częściowy x_ {1}}}, \ kropki, {\ Frac {\ częściowy f} {\ częściowy x_ {n}}} \ po prawej),}$

tak, że df _x ( v ) jest dane przez mnożenie macierzy . Zakładając standardową metrykę euklidesową na R ⁿ , gradient jest wtedy odpowiednim wektorem kolumnowym, to znaczy

${\ Displaystyle (\ nabla f) _ {i} = df_ {i} ^ {\ mathsf {T}}.}$

Aproksymacja liniowa do funkcji

Najlepsze przybliżenie liniowe funkcji można wyrazić w postaci gradientu, a nie pochodnej. Gradient funkcji f z przestrzeni euklidesowej R ⁿ do R w dowolnym punkcie x ₀ w R ⁿ charakteryzuje najlepsze przybliżenie liniowe do f w x ₀ . Przybliżenie jest następujące:

${\ Displaystyle f (x) \ ok. f (x_ {0}) + (\ nabla f) _ {x_ {0}} \ cdot (x-x_ {0})}$

dla x blisko x ₀ , gdzie (∇ f  ) _{x 0} jest gradientem f obliczonym w x ₀ , a kropka oznacza iloczyn skalarny na R ⁿ . To równanie jest równoważne pierwszym dwóm członom w wielowymiarowym rozwinięciu f w szeregu Taylora w punkcie x ₀ .

Związek z pochodną Fréchet

Niech U będzie zbiorem otwartym w R ⁿ . Jeżeli funkcja F  : U → R jest różniczkowalną, wówczas różniczka f jest pochodna Fréchet z F . Zatem ∇ f jest funkcją od U do przestrzeni R ⁿ taką, że

${\ Displaystyle \ lim _ {h \ do 0} {\ Frac {| f (x + h) - f (x) - \ nabla f (x) \ cdot h |} {\ | h \ |}} = 0 ,}$

gdzie · jest iloczynem skalarnym.

W konsekwencji, zwykłe własności pochodnej obowiązują dla gradientu, chociaż gradient nie jest sam w sobie pochodną, ​​ale raczej dualną do pochodnej:

Liniowość

Gradient jest liniowy w tym sensie, że jeśli f i g są dwiema funkcjami o wartościach rzeczywistych, różniczkowalnymi w punkcie a ∈ R ⁿ , a α i β są dwiema stałymi, to αf + βg jest różniczkowalna w a , a ponadto

${\ Displaystyle \ nabla \ lewo (\ alfa f + \ beta g \ po prawej) (a) = \ alfa \ nabla f (a) + \ beta \ nabla g (a).}$

Zasada produktu

Jeśli f i g są funkcjami o wartościach rzeczywistych różniczkowalnymi w punkcie a ∈ R ⁿ , to reguła iloczynu zakłada, że iloczyn fg jest różniczkowalny w a , oraz

${\ Displaystyle \ nabla (fg) (a) = f (a) \ nabla g (a) + g (a) \ nabla f (a).}$

Zasada łańcuchowa

Załóżmy, że f  : A → R jest funkcją o wartościach rzeczywistych zdefiniowaną na podzbiorze A z R ⁿ , oraz że f jest różniczkowalna w punkcie a . Istnieją dwie formy reguły łańcucha mającej zastosowanie do gradientu. Najpierw załóżmy, że funkcja g jest krzywą parametryczną ; czyli funkcja g  : I → R ⁿ odwzorowuje podzbiór I ⊂ R na R ⁿ . Jeśli g jest różniczkowalna w punkcie c ∈ I takim, że g ( c ) = a , wtedy

${\ Displaystyle (f \ circ g) '(c) = \ nabla f (a) \ cdot g '(c)}$

gdzie ∘ jest operatorem kompozycji : (  f  ∘  g ) ( x ) = f ( g ( x ) ) .

Bardziej ogólnie, jeśli zamiast tego I ⊂ R ^k , to zachodzi:

${\ Displaystyle \ nabla (f \ circ g) (c) = {\ duży (} Dg (c) {\ duży)} ^ {\ mathsf {T}} {\ duży (} \ nabla f (a) {\ duża )},}$

gdzie ( Dg ) ^T oznacza transponowaną macierz Jakobianu .

Dla drugiej postaci reguły łańcucha załóżmy, że h  : I → R jest funkcją o wartościach rzeczywistych na podzbiorze I z R , i że h jest różniczkowalna w punkcie f ( a ) ∈ I . Następnie

${\ Displaystyle \ nabla (h \ circ f) (a) = h '{\ duży (} f (a) {\ duży )} \ nabla f (a).}$

Dalsze właściwości i zastosowania

Zestawy poziomów

Powierzchnia pozioma lub izopowierzchnia to zbiór wszystkich punktów, w których jakaś funkcja ma określoną wartość.

Jeśli f jest różniczkowalne, to iloczyn skalarny (∇ f  ) _x ⋅ v gradientu w punkcie x z wektorem v daje pochodną kierunkową f w x w kierunku v . Wynika z tego, że w tym przypadku, gradient F jest prostopadły do zestawów poziomu o f . Na przykład płaska powierzchnia w przestrzeni trójwymiarowej jest zdefiniowana równaniem postaci F ( x , y , z ) = c . Gradient F jest wtedy normalny do powierzchni.

Bardziej ogólnie, każda osadzona hiperpowierzchnia w rozmaitości Riemanna może być wycinana równaniem postaci F ( P )=0 tak, że dF nie jest nigdzie zerem. Gradient F jest wtedy normalny do hiperpowierzchni.

Podobnie, afiniczny algebraiczna hiperpowierzchni mogą być zdefiniowane za pomocą równania F ( x ₁ , ..., x _n ) = 0 , gdzie K jest wielomianem. Gradient F wynosi zero w punkcie osobliwym hiperpowierzchni (jest to definicja punktu osobliwego). W punkcie nieosobliwym jest to niezerowy wektor normalny.

Konserwatywne pola wektorowe i twierdzenie o gradiencie

Gradient funkcji nazywany jest polem gradientowym. Pole gradientu (ciągłego) jest zawsze konserwatywnym polem wektorowym : jego całka krzywoliniowa wzdłuż dowolnej ścieżki zależy tylko od punktów końcowych ścieżki i może być oceniona przez twierdzenie gradientowe (podstawowe twierdzenie rachunku różniczkowego dla całek krzywoliniowych). I odwrotnie, (ciągłe) konserwatywne pole wektorowe jest zawsze gradientem funkcji.

Uogólnienia

Jakobian

Jakobian matryca jest uogólnieniem gradient funkcji wektora wartościach od kilku zmiennych różniczkowalnych mapy między euklidesowych , lub bardziej ogólnie, rozdzielaczy . Dalszym uogólnieniem funkcji między przestrzeniami Banacha jest pochodna Frécheta .

Załóżmy, że f  : ℝ ⁿ → ℝ ^m jest funkcją taką, że każda z jej pochodnych cząstkowych pierwszego rzędu istnieje na ℝ ⁿ . Wtedy jakobian macierz f definiuje się jako macierz m × n , oznaczoną przez lub po prostu . ( I , j ) th wpisu . Jawnie ${\ Displaystyle \ mathbf {J} _ {\ mathbb {f}} (\ mathbb {x})}$${\ Displaystyle \ mathbf {J}}$${\ Displaystyle \ mathbf {J} _ {ij} = {\ Frac {\ częściowy f_ {i}} {\ częściowy x_ {j}}}}$

${\ Displaystyle \ mathbf {J} = {\ zacząć {bmatrix} {\ dfrac {\ częściowy \ mathbf {f}} {\ częściowy x_ {1}}} i \ cdots i {\ dfrac {\ częściowy \ mathbf {f } }{\częściowy x_{n}}}\end{bmatrix}}={\begin{bmatrix}\nabla ^{\mathsf {T}}f_{1}\\\vdots \\\nabla ^{\mathsf {T}}f_{m}\end{bmatrix}}={\begin{bmatrix}{\dfrac {\partial f_{1}}{\partial x_{1}}}&\cdots &{\dfrac {\ częściowe f_{1}}{\partial x_{n}}}\\\vdots &\ddots &\vdots \\{\dfrac {\partial f_{m}}{\partial x_{1}}}&\cdots &{\dfrac {\częściowy f_{m}}{\częściowy x_{n}}}\end{bmatrix}}.}$

Gradient pola wektorowego

Ponieważ całkowita pochodna pola wektorowego jest odwzorowaniem liniowym z wektorów na wektory, jest to wielkość tensorowa .

We współrzędnych prostokątnych gradient pola wektorowego f = (  f ¹ , f ² , f ³ ) jest określony wzorem:

${\ Displaystyle \ nabla \ mathbf {f} = g ^ {jk} {\ Frac {\ częściowy f ^ {i}} \ częściowy x ^ {j}}} \ mathbf {e} _ {i} \ czasami \ mathbf {e} _{k},}$

(gdzie zapis sumowanie Einsteina jest używany, a produkt napinacz wektorów e _I a E _K jest dwójkowym napinacz typu (2,0)). Ogólnie rzecz biorąc, wyrażenie to jest równe transpozycji macierzy Jakobianu:

${\ Displaystyle {\ Frac {\ częściowy f ^ {i}} {\ częściowy x ^ {j}}} = {\ Frac {\ częściowy (f ^ {1}, f ^ {2}, f ^ {3}) )}{\częściowy (x^{1},x^{2},x^{3})}}.}$

We współrzędnych krzywoliniowych, lub bardziej ogólnie na zakrzywionej rozmaitości , gradient obejmuje symbole Christoffela :

${\ Displaystyle \ nabla \ mathbf {f} = g ^ {jk} \ lewo ({\ Frac {\ częściowy f ^ {i}} {\ częściowy x ^ {j}}} + {\ Gamma ^ {i}} _{jl}f^{l}\right)\mathbf {e} _{i}\otimes \mathbf {e} _{k},}$

gdzie g ^jk to składowe odwrotnego tensora metrycznego, a e _i to wektory bazowe współrzędnych.

Wyrażony bardziej niezmiennie, gradient pola wektorowego f można zdefiniować za pomocą połączenia Levi-Civita i tensora metrycznego:

${\ Displaystyle \ nabla ^ {a} f ^ {b} = g ^ {ac} \ nabla _ {c} f ^ {b}}$

gdzie ∇ _c jest połączeniem.

Rozmaitości riemannowskie

Dla dowolnej gładkiej funkcji f na rozmaitości Riemanna ( M , g ) gradient f jest polem wektorowym ∇ f takim, że dla dowolnego pola wektorowego X ,

${\ Displaystyle g (\ nabla f, X) = \ częściowy _ {X} f}$

to jest,

${\ Displaystyle g_ {x} {\ duży (} (\ nabla f) _ {x}, X_ {x} {\ duży )} = (\ częściowy _ {X} f) (x)}$

gdzie g _x ( , ) oznacza iloczyn skalarny wektorów stycznych w x zdefiniowanym przez metrykę g , a ∂ _X  f jest funkcją, która przyjmuje dowolny punkt x ∈ M do kierunkowej pochodnej f w kierunku X , obliczonej w x . Innymi słowy, na wykresie współrzędnych φ od otwartego podzbioru M do otwartego podzbioru R ⁿ , (∂ _X  f  )( x ) jest dane wzorem:

${\ Displaystyle \ suma _ {j = 1} ^ {n} X ^ {j} {\ duży (} \ varphi (x) {\ duży)} {\ Frac {\ częściowy} {\ częściowy x_ {j}} }(f\circ \varphi ^{-1}){\Bigg |}_{\varphi (x)},}$

gdzie X ^j oznacza j- tą składową X na tym wykresie współrzędnych.

Tak więc lokalna forma gradientu przyjmuje postać:

${\ Displaystyle \ nabla f = g ^ {ik} {\ Frac {\ częściowy f} {\ częściowy x ^ {k}}} {\ textbf {e}} _ {i}}.$

Uogólniając przypadek M = R ⁿ , gradient funkcji jest powiązany z jej zewnętrzną pochodną, ​​ponieważ

${\ Displaystyle (\ częściowy _ {X} f) (x) = (df) _ {x} (X_ {x}).}$

Dokładniej, gradient ∇ f jest polem wektorowym związanym z różniczkową 1-formą df przy użyciu izomorfizmu muzycznego

${\ Displaystyle \ ostry = \ ostry ^ {g} \ dwukropek T ^ {*} M \ do TM}$

(nazywany „ostrym”) zdefiniowanym przez metrykę g . Związek między pochodną zewnętrzną a gradientem funkcji na R ⁿ jest szczególnym przypadkiem tego, w którym metryka jest metryką płaską podaną przez iloczyn skalarny.

Zobacz też

• Kędzior
• Rozbieżność
• Czterogradientowy
• Hesja macierz
• Pochyl gradient

Uwagi

Bibliografia

• Bachman, David (2007), Advanced Calculus Demystified , New York: McGraw-Hill , ISBN 978-0-07-148121-2
• Beauregard, Raymond A.; Fraleigh, John B. (1973), Pierwszy kurs algebry liniowej: z opcjonalnym wprowadzeniem do grup, pierścieni i pól , Boston: Houghton Mifflin Company , ISBN 0-395-14017-X
• Downing, Douglas, Ph.D. (2010), Barron's EZ Calculus , New York: Barron's , ISBN 978-0-7641-4461-5
• Dubrowin, BA; Fomenko, AT; Nowikow SP (1991). Współczesna geometria — metody i zastosowania: Część I: Geometria powierzchni, grup transformacji i pól . Teksty magisterskie z matematyki (wyd. 2). Skoczek. Numer ISBN 978-0-387-97663-1.
• Harper, Charlie (1976), Wprowadzenie do fizyki matematycznej , New Jersey: Prentice-Hall , ISBN 0-13-487538-9
• Kreyszig, Erwin (1972), Advanced Engineering Mathematics (3rd ed.), New York: Wiley , ISBN 0-471-50728-8
• „McGraw Hill Encyklopedia Nauki i Technologii”. Encyklopedia Nauki i Technologii McGraw-Hill (wyd. 10). Nowy Jork: McGraw-Hill . 2007. ISBN 978-0-07-144143-8.
• Moise, Edwin E. (1967), Rachunek: Complete , Czytanie: Addison-Wesley
• Protter, Murray H.; Morrey, Jr., Charles B. (1970), College Rachunek z geometrią analityczną (2nd ed.), Czytanie: Addison-Wesley , LCCN  76087042
• Schey, HM (1992). Div, Grad, Curl i All That (wyd. 2). WW Norton. Numer ISBN 0-393-96251-2. OCLC  25048561 .
• Stoker, JJ (1969), Geometria różniczkowa , New York: Wiley , ISBN 0-471-82825-4
• Swokowski hrabia W.; Olinick, Michael; Pensa, Dennisa; Cole, Jeffery A. (1994), Rachunek (wyd. 6), Boston: PWS Publishing Company, ISBN 0-534-93624-5

Dalsza lektura

• Korn, Theresa M .; Korn, Granino Artur (2000). Podręcznik matematyczny dla naukowców i inżynierów: Definicje, twierdzenia i formuły odniesienia i przeglądu . Publikacje Dovera. s. 157–160. Numer ISBN 0-486-41147-8. OCLC  43864234 .

Zewnętrzne linki

• „Gradient” . Akademia Khana .
• Kuptsov, LP (2001) [1994], "Gradient" , Encyklopedia Matematyki , EMS Press.
• Weisstein, Eric W. „Gradient” . MatematykaŚwiat .