Homomorfizm grupowy - Group homomorphism

Obraz homomorfizmu grupowego ( h ) od G (po lewej) do H (po prawej). Mniejszy owal wewnątrz H to wizerunek h . N jest jądro o h i aN jest warstwa z N .

Struktura algebraiczna → Teoria grup Teoria grup
Podstawowe pojęcia Podgrupa Normalna podgrupa Grupa ilorazów Produkt (pół) bezpośredni Homomorfizmy grupowe jądro wizerunek suma bezpośrednia produkt wieniec prosty skończone nieskończony ciągły mnożny przyłączeniowy cykliczny abelowy dwuścienny nilpotent rozpuszczalny Słowniczek teorii grup Lista tematów teorii grup
Grupy skończone Klasyfikacja skończonych grup prostych cykliczny zmienny Typ kłamstwa sporadyczny Twierdzenie Cauchy'ego Twierdzenie Lagrange'a Twierdzenia Sylowa Twierdzenie Halla grupa p Elementarna grupa abelowa Grupa Frobenius Mnożnik Schura Grupa symetryczna S n Klein cztery grupy V Grupa dwuścienna D n Grupa kwaternionów Q Grupa dicykliczna Dic n
Dyskretne grupy Kraty Liczby całkowite ( Z ) Bezpłatna grupa Grupy modułowe PSL (2, Z ) SL (2, Z ) Grupa arytmetyczna Krata Grupa hiperboliczna
Grupy topologiczne i Lie Elektrozawór okrąg Ogólny liniowy GL ( n ) Specjalny liniowy SL ( n ) Ortogonalne O ( n ) Euklidesa E ( n ) Specjalne ortogonalne SO ( n ) Jednostkowe U ( n ) Specjalne jednostkowe SU ( n ) Symplectic Sp ( n ) G 2 F 4 E 6 E 7 E 8 Lorentz Poincaré Konformalne Dyfeomorfizm Pętla Nieskończona wymiarowa grupa Lie O (∞) SU (∞) Sp (∞)
Grupy algebraiczne Liniowa grupa algebraiczna Grupa redukcyjna Odmiana abelowa Krzywa eliptyczna
v t mi

W matematyce , biorąc pod uwagę dwie grupy ( G , ∗) i ( H , ·), homomorfizm grupowy od ( G , ∗) do ( H , ·) jest funkcją h  : G → H taką, że dla wszystkich u i v w G to trzyma

${\ Displaystyle h (u * v) = h (u) \ cdot h (v)}$

gdzie operacja grupa z lewej strony równania jest to, że G i po prawej stronie tej z H .

Z tej własności można wywnioskować, że h odwzorowuje element tożsamości e _G z G na element tożsamości e _H z H ,

${\ Displaystyle h (e_ {G}) = e_ {H}}$

a także odwraca odwrotność do odwrotności w tym sensie

${\ Displaystyle h \ lewo (u ^ {- 1} \ prawej) = h (u) ^ {- 1}. \,}$

Stąd można powiedzieć, że h „jest zgodne ze strukturą grupy”.

Starsze zapisy homomorfizmu h ( x ) mogą mieć postać x ^h lub x _h , chociaż można to pomylić jako indeks lub ogólny indeks dolny. W teorii automatów czasami homomorfizmy są zapisywane po prawej stronie ich argumentów bez nawiasów, tak że h ( x ) staje się po prostu xh .

W obszarach matematyki, w których rozważa się grupy obdarzone dodatkową strukturą, homomorfizm oznacza czasami mapę uwzględniającą nie tylko strukturę grupową (jak wyżej), ale także dodatkową strukturę. Na przykład często wymagany jest homomorfizm grup topologicznych, aby był ciągły.

Intuicja

Celem zdefiniowania homomorfizmu grupowego jest stworzenie funkcji, które zachowują strukturę algebraiczną. Równoważna definicja homomorfizmu grupowego to: Funkcja h  : G → H jest homomorfizmem grupowym, jeśli kiedykolwiek

a ∗ b = c   mamy   h ( a ) ⋅ h ( b ) = h ( c ).

Innymi słowy, grupa H ma w pewnym sensie podobną strukturę algebraiczną do G i homomorfizm h to zachowuje.

Rodzaje

Monomorfizm

Grupowy homomorfizm, który jest iniekcyjny (lub jeden do jednego); tj. zachowuje wyrazistość.

Epimorfizm

Homomorfizm grupowy, który jest suriektywny (lub na); tzn. dociera do każdego punktu w kodomenie.

Izomorfizm

Homomorfizm grupowy, który jest bijektywny ; tj. iniekcyjne i surjektywne. Jego odwrotnością jest również homomorfizm grupowy. W tym przypadku grupy G i H nazywane są izomorficznymi ; różnią się jedynie zapisem ich elementów i są identyczne pod względem praktycznym.

Endomorfizm

Homomorfizm, h : G → G ; domena i kodomena są takie same. Zwany także endomorfizm z G .

Automorfizm

Endomorfizm, który jest bijektywny, a zatem izomorfizm. Zbiór wszystkich automorfizmy z grupy G , z kompozycją funkcjonalnej, działania tworzy sobie grupę, na grupę automorfizm o G . Jest oznaczony przez Aut ( G ). Na przykład grupa automorfizmu ( Z , +) zawiera tylko dwa elementy, transformację tożsamości i mnożenie przez −1; jest izomorficzny Z / 2, Z .

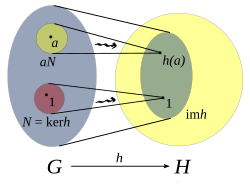
Obraz i jądro

Definiujemy jądro h jako zbiór elementów w G, które są odwzorowane na tożsamość w H

${\ displaystyle \ operatorname {ker} (h) \ equiv \ lewo \ {u \ in G \ colon h (u) = e_ {H} \ prawo \}.}$

a obraz o godz być

${\ displaystyle \ operatorname {im} (h) \ equiv h (G) \ equiv \ lewo \ {h (u) \ dwukropek u \ in G \ prawo \}.}$

Jądro i obraz homomorfizmu można interpretować jako pomiar tego, jak blisko jest do bycia izomorfizmem. Te pierwsze Izomorfizm twierdzenie stwierdza się, że obraz homomorfizmu grupy, h ( G ) jest izomorficzny grupy iloraz G / ker godz .

Jądro h jest normalnie podgrupy z G i obraz H jest podgrupa o H :

${\ Displaystyle {\ rozpocząć {wyrównane} h \ lewo (g ^ {- 1} \ Circ u \ Circ g \ prawej) & = h (g) ^ {- 1} \ cdot h (u) \ cdot h (g ) \\ & = h (g) ^ {- 1} \ cdot e_ {H} \ cdot h (g) \\ & = h (g) ^ {- 1} \ cdot h (g) = e_ {H} . \ end {aligned}}}$

Jeśli i tylko wtedy, gdy ker ( h ) = { e _G }, homomorfizm, h , jest monomorfizmem grupowym ; tj. h to iniekcja (jeden do jednego). Wstrzyknięcie bezpośrednio daje unikalny element w jądrze, a unikalny element w jądrze daje iniekcję:

${\ Displaystyle {\ rozpocząć {wyrównane} && h (g_ {1}) & = h (g_ {2}) \\\ Leftrightarrow && h (g_ {1}) \ cdot h (g_ {2}) ^ {- 1} & = e_ {H} \\\ Leftrightarrow && h \ left (g_ {1} \ circ g_ {2} ^ {- 1} \ right) & = e_ {H}, \ \ operatorname {ker} (h) = \ {e_ {G} \} \\\ Rightarrow && g_ {1} \ circ g_ {2} ^ {- 1} & = e_ {G} \\\ Leftrightarrow && g_ {1} & = g_ {2} \ end {aligned }}}$

Przykłady

• Rozważmy cykliczną grupę Z / 3 Z = {0, 1, 2} i grupę liczb całkowitych Z z dodatkiem. Mapa h  : Z → Z / 3 Z z h ( u ) = u mod 3 jest homomorfizmem grupowym. Jest suriektywny, a jego jądro składa się ze wszystkich liczb całkowitych, które są podzielne przez 3.

• Wykładniczy mapę daje homomorfizmem grupy z grupy liczb rzeczywistych R z oprócz grupy niezerowych liczb rzeczywistych R * z mnożenia. Jądro to {0}, a obraz składa się z dodatnich liczb rzeczywistych.
• Mapa wykładnicza daje również homomorfizm grupowy z grupy liczb zespolonych C z dodatkiem do grupy niezerowych liczb zespolonych C * z mnożeniem. Ta mapa jest suriektywna i ma jądro {2π ki  : k ∈ Z }, jak widać ze wzoru Eulera . Pola takie jak R i C, które mają homomorfizmy od ich grupy addytywnej do ich grupy multiplikatywnej, są więc nazywane polami wykładniczymi .

Kategoria grup

Jeśli h  : G → H i K  : H → K są homomorfizmy grupy, a więc jest K ∘ H  : G → K . To pokazuje, że klasa wszystkich grup, wraz z homomorfizmami grupowymi jako morfizmami, tworzy kategorię .

Homomorfizmy grup abelowych

Jeśli G i H są grupami abelowymi (tj. Przemiennymi), to zbiór Hom ( G , H ) wszystkich homomorfizmów grupowych od G do H jest sam w sobie grupą abelową: suma h + k dwóch homomorfizmów jest określona przez

( H + K ) ( U ) = h ( u ) + K ( u ) dla wszystkich u w G .

Przemienność H jest potrzebna, aby udowodnić, że h + k jest znowu homomorfizmem grupowym.

Dodanie homomorfizmów jest zgodne ze składem homomorfizmów w następującym sensie: jeśli f jest w Hom ( K , G ) , h , k są elementami Hom ( G , H ) , a g jest w Hom ( H , L ) , następnie

( h + k ) ∘ f = ( h ∘ f ) + ( k ∘ f )    i    g ∘ ( h + k ) = ( g ∘ h ) + ( g ∘ k ) .

Ponieważ kompozycja jest asocjacyjne , pokazuje to, że zestaw zakończenia ( G ) wszystkich endomorfizm od An grupa przemienna tworzy pierścień , na pierścień endomorfizm o G . Na przykład, pierścień endomorfizm abelian grupy składającej się z bezpośredniego sumy z m kopii Z / n Z jest izomorficzny pierścienia m -by- m matryce z wpisami Z / n Z . Z powyższej zgodności wynika również, że kategoria wszystkich grup abelowych z grupowymi homomorfizmami tworzy kategorię przedaddytywną ; istnienie sum bezpośrednich i dobrze zachowujących się jąder czyni z tej kategorii prototypowy przykład kategorii abelowej .

Zobacz też

Bibliografia

• Dummit, DS; Foote, R. (2004). Algebra abstrakcyjna (3rd ed.). Wiley. s. 71–72. ISBN   978-0-471-43334-7 .
• Lang, Serge (2002), Algebra , Graduate Texts in Mathematics , 211 (poprawione wydanie trzecie), New York: Springer-Verlag, ISBN   978-0-387-95385-4 , MR   1878556 , Zbl   0984.00001

Zewnętrzne linki

• Rowland, Todd & Weisstein, Eric W. „Homomorfizm grupowy” . MathWorld .