Kodowanie Huffmana - Huffman coding

| Zwęglać | Freq | Kod |
|---|---|---|
| przestrzeń | 7 | 111 |
| za | 4 | 010 |
| mi | 4 | 000 |
| fa | 3 | 1101 |
| h | 2 | 1010 |
| ja | 2 | 1000 |
| m | 2 | 0111 |
| nie | 2 | 0010 |
| s | 2 | 1011 |
| t | 2 | 0110 |
| ja | 1 | 11001 |
| o | 1 | 00110 |
| p | 1 | 10011 |
| r | 1 | 11000 |
| ty | 1 | 00111 |
| x | 1 | 10010 |
W informatyce i teorii informacji , wykorzystując kod Huffmana jest szczególnym rodzajem optymalnego kodu prefiks , który jest powszechnie stosowany do kompresji danych, bezstratny . Proces odnalezienia lub wykorzystania takiego kodu przebiega za pomocą kodowania Huffmana , algorytmu opracowanego przez Davida A. Huffmana, gdy był on doktorantem. student na MIT i opublikował w 1952 roku artykuł „Metoda konstrukcji kodów minimalnej redundancji”.
Dane wyjściowe algorytmu Huffmana można przeglądać jako tabelę kodów o zmiennej długości do kodowania symbolu źródłowego (takiego jak znak w pliku). Algorytm wyprowadza tę tabelę z szacowanego prawdopodobieństwa lub częstości występowania ( wagi ) dla każdej możliwej wartości symbolu źródłowego. Podobnie jak w innych metodach kodowania entropijnego , więcej powszechnych symboli jest ogólnie reprezentowanych przy użyciu mniejszej liczby bitów niż mniej popularnych symboli. Metoda Huffmana może być efektywnie zaimplementowana, znajdując kod w czasie liniowo do liczby wag wejściowych, jeśli te wagi są sortowane. Jednakże, chociaż optymalne wśród metod kodujących symbole oddzielnie, kodowanie Huffmana nie zawsze jest optymalne wśród wszystkich metod kompresji - jest zastępowane kodowaniem arytmetycznym lub asymetrycznymi systemami liczbowymi, jeśli wymagany jest lepszy współczynnik kompresji.
Historia
W 1951 David A. Huffman i jego koledzy z MIT z teorii informacji mieli do wyboru pracę semestralną lub egzamin końcowy . Profesor Robert M. Fano przypisał pracę semestralną na temat znalezienia najbardziej wydajnego kodu binarnego. Huffman, nie mogąc udowodnić, że żadne kody są najskuteczniejsze, już miał się poddać i rozpocząć naukę do finału, kiedy wpadł na pomysł użycia posortowanego według częstotliwości drzewa binarnego i szybko udowodnił, że ta metoda jest najbardziej wydajna.
W ten sposób Huffman prześcignął Fano, który współpracował z wynalazcą teorii informacji Claudem Shannonem, aby opracować podobny kod. Budowanie drzewa od dołu do góry gwarantowało optymalność, w przeciwieństwie do podejścia odgórnego kodowania Shannona-Fano .
Terminologia
Kodowanie Huffmana wykorzystuje specyficzną metodę wyboru reprezentacji dla każdego symbolu, w wyniku czego otrzymuje się kod przedrostkowy (czasami nazywany „kodami bez przedrostków”, to znaczy ciąg bitów reprezentujący określony symbol nigdy nie jest przedrostkiem ciągu bitów reprezentującego jakikolwiek inny symbol). Kodowanie Huffmana jest tak rozpowszechnioną metodą tworzenia kodów prefiksowych, że termin „kod Huffmana” jest powszechnie używany jako synonim „kodu prefiksowego”, nawet jeśli taki kod nie jest wytwarzany przez algorytm Huffmana.
Definicja problemu
Nieformalny opis
- Dany
- Zestaw symboli i ich wag (zwykle proporcjonalnych do prawdopodobieństw).
- Odnaleźć
- Kod binarny prefix-wolny (zestaw słów kodowych) z minimum oczekuje długość słowa kodowego (równoważnie, drzewo z minimalnej ważonej długości ścieżki od korzenia ).
Sformalizowany opis
Wejście .
Alfabet , który jest symbolem alfabetu wielkości .
Krotka , która jest krotką (dodatnich) wag symbolu (zwykle proporcjonalnych do prawdopodobieństw), tj . . Wyjście .
Code , który jest krotką (binarnych) słów kodowych, gdzie jest słowem kodowym dla . Cel .
Niech będzie ważoną długością ścieżki kodu . Warunek: dla dowolnego kodu .
Przykład
Podajemy przykład wyniku kodowania Huffmana dla kodu z pięcioma znakami i podanymi wagami. Nie będziemy sprawdzać, czy minimalizuje L we wszystkich kodach, ale obliczymy L i porównamy je z entropią Shannona H danego zestawu wag; wynik jest prawie optymalny.
| Wejście ( A , W ) | Symbol ( a i ) | za | b | do | re | mi | Suma |
|---|---|---|---|---|---|---|---|
| Wagi ( w i ) | 0,10 | 0,15 | 0,30 | 0,16 | 0,29 | = 1 | |
| Wyjście C | Słowa kodowe ( c i ) |
010
|
011
|
11
|
00
|
10
|
|
| Długość słowa kodowego (w bitach) ( l i ) |
3 | 3 | 2 | 2 | 2 | ||
| Udział w ważonej długości ścieżki ( l i w i ) |
0,30 | 0,45 | 0,60 | 0,32 | 0,58 | L ( C ) = 2,25 | |
| Optymalność | Budżet prawdopodobieństwa (2 − l i ) |
1/8 | 1/8 | 1/4 | 1/4 | 1/4 | = 1,00 |
| Zawartość informacji (w bitach) (− log 2 w i ) ≈ |
3,32 | 2,74 | 1,74 | 2,64 | 1,79 | ||
| Wkład do entropii (− w i log 2 w i ) |
0,332 | 0,411 | 0,521 | 0,423 | 0,518 | H ( A ) = 2,205 |
W przypadku każdego kodu, który jest biunique , co oznacza, że kod jest jednoznacznie dekodowany , suma budżetów prawdopodobieństwa we wszystkich symbolach jest zawsze mniejsza lub równa jeden. W tym przykładzie suma jest ściśle równa jeden; w rezultacie kod nazywany jest kompletnym kodem. Jeśli tak nie jest, zawsze można wyprowadzić równoważny kod, dodając dodatkowe symbole (z powiązanymi prawdopodobieństwami zerowymi ), aby kod był kompletny, zachowując jednocześnie biunique .
Jak określono Shannon (1948) , zawartość informacyjna h (w bitach) dla każdego symbolu I z nie-zerowej prawdopodobieństwo
Entropii H (w bitach), to suma ważone we wszystkich symboli i z nie-zerowym prawdopodobieństwa wag I , o zawartości informacyjnej każdego symbolu:
(Uwaga: symbol z zerowym prawdopodobieństwem ma zerowy udział w entropii, ponieważ dla uproszczenia symbole z zerowym prawdopodobieństwem można pominąć w powyższym wzorze.)
W konsekwencji twierdzenia Shannona o kodowaniu źródłowym entropia jest miarą najmniejszej długości słowa kodowego, jaka jest teoretycznie możliwa dla danego alfabetu z powiązanymi wagami. W tym przykładzie średnia ważona długość słowa kodowego wynosi 2,25 bitów na symbol, tylko nieco więcej niż obliczona entropia 2,205 bitów na symbol. Zatem ten kod jest nie tylko optymalny w tym sensie, że żaden inny możliwy do wykonania kod nie działa lepiej, ale jest bardzo zbliżony do teoretycznej granicy ustalonej przez Shannona.
Ogólnie kod Huffmana nie musi być unikalny. Zatem zbiór kodów Huffmana dla danego rozkładu prawdopodobieństwa jest niepustym podzbiorem kodów minimalizujących dla tego rozkładu prawdopodobieństwa. (Jednak dla każdego przypisania minimalizującego długość słowa kodowego istnieje co najmniej jeden kod Huffmana o tych długościach.)
Technika podstawowa
Kompresja
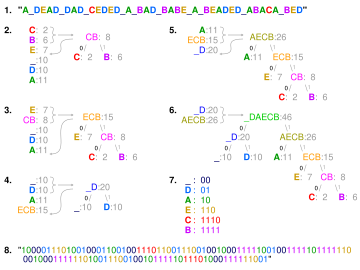
”. W krokach od 2 do 6 litery są sortowane według rosnącej częstotliwości, a najmniej częste dwie na każdym kroku są łączone i ponownie wstawiane na listę, a następnie konstruowane jest częściowe drzewo. Ostatnie drzewo w kroku 6 jest przeszukiwane w celu wygenerowania słownika w kroku 7. Krok 8 wykorzystuje go do zakodowania wiadomości.

| Symbol | Kod |
|---|---|
| a1 | 0 |
| a2 | 10 |
| a3 | 110 |
| a4 | 111 |
Technika działa poprzez tworzenie binarnego drzewa węzłów. Mogą one być przechowywane w zwykłej tablicy , której wielkość zależy od liczby symboli . Węzeł może być węzłem liścia lub węzłem wewnętrznym . Początkowo wszystkie węzły to węzły liściowe, które zawierają sam symbol , wagę (częstotliwość pojawiania się) symbolu oraz opcjonalnie link do węzła nadrzędnego, co ułatwia odczytanie kodu (w odwrotnej kolejności) zaczynając od węzła liścia . Węzły wewnętrzne zawierają wagę , linki do dwóch węzłów podrzędnych i opcjonalny link do węzła nadrzędnego . Zgodnie z powszechną konwencją, bit '0' reprezentuje lewe dziecko, a bit '1' reprezentuje prawe dziecko. Gotowe drzewo ma do węzłów liściowych i węzłów wewnętrznych. Drzewo Huffmana, które pomija nieużywane symbole, daje najbardziej optymalne długości kodu.
Proces rozpoczyna się od węzłów liści zawierających prawdopodobieństwa symbolu, który reprezentują. Następnie proces pobiera dwa węzły z najmniejszym prawdopodobieństwem i tworzy nowy węzeł wewnętrzny mający te dwa węzły jako dzieci. Waga nowego węzła jest ustawiona na sumę wagi dzieci. Następnie stosujemy ten proces ponownie, na nowym węźle wewnętrznym i na pozostałych węzłach (tzn. wykluczamy dwa węzły liści), powtarzamy ten proces, aż pozostanie tylko jeden węzeł, który jest korzeniem drzewa Huffmana.
Najprostszy algorytm konstrukcji wykorzystuje kolejkę priorytetową, w której węzeł o najmniejszym prawdopodobieństwie ma najwyższy priorytet:
- Utwórz węzeł liścia dla każdego symbolu i dodaj go do kolejki priorytetowej.
- Gdy w kolejce jest więcej niż jeden węzeł:
- Usuń dwa węzły o najwyższym priorytecie (najmniejsze prawdopodobieństwo) z kolejki
- Utwórz nowy węzeł wewnętrzny z tymi dwoma węzłami jako dziećmi iz prawdopodobieństwem równym sumie prawdopodobieństw dwóch węzłów.
- Dodaj nowy węzeł do kolejki.
- Pozostały węzeł jest węzłem głównym, a drzewo jest kompletne.
Ponieważ wydajne struktury danych kolejki priorytetowej wymagają czasu O(log n ) na wstawienie, a drzewo z n liśćmi ma 2 n -1 węzłów, ten algorytm działa w czasie O( n log n ), gdzie n jest liczbą symboli.
Jeśli symbole są sortowane według prawdopodobieństwa, istnieje metoda czasu liniowego (O( n )) do utworzenia drzewa Huffmana przy użyciu dwóch kolejek , pierwsza zawiera wagi początkowe (wraz ze wskaźnikami do powiązanych liści) i wagi połączone (wraz ze wskaźnikami do drzew) znajdują się z tyłu drugiej kolejki. Gwarantuje to, że najniższa waga jest zawsze utrzymywana z przodu jednej z dwóch kolejek:
- Zacznij od tylu liści, ile jest symboli.
- Umieść wszystkie węzły liści w kolejce do pierwszej kolejki (według prawdopodobieństwa w porządku rosnącym, aby najmniej prawdopodobny element znajdował się na początku kolejki).
- Gdy w kolejkach jest więcej niż jeden węzeł:
- Zdekolejkuj dwa węzły o najniższej wadze, badając fronty obu kolejek.
- Utwórz nowy węzeł wewnętrzny z dwoma właśnie usuniętymi węzłami jako dziećmi (każdy węzeł może być dowolnym z nich) i sumą ich wag jako nową wagą.
- Umieść nowy węzeł w kolejce z tyłu drugiej kolejki.
- Pozostały węzeł to węzeł główny; drzewo zostało teraz wygenerowane.
Po wygenerowaniu drzewa Huffmana przechodzi się do wygenerowania słownika, który odwzorowuje symbole na kody binarne w następujący sposób:
- Zacznij od bieżącego węzła ustawionego na root.
- Jeśli węzeł nie jest węzłem liścia, oznacz krawędź do lewego dziecka jako 0, a krawędź do prawego dziecka jako 1 . Powtórz ten proces zarówno dla lewego dziecka, jak i prawego dziecka.
Ostateczne kodowanie dowolnego symbolu jest następnie odczytywane przez łączenie etykiet na krawędziach wzdłuż ścieżki od węzła głównego do symbolu.
W wielu przypadkach przy wyborze algorytmu nie ma większego znaczenia złożoność czasowa, ponieważ n to liczba symboli w alfabecie, która zazwyczaj jest bardzo małą liczbą (w porównaniu do długości wiadomości do zakodowania); podczas gdy analiza złożoności dotyczy zachowania, gdy n rośnie do bardzo dużego.
Ogólnie korzystne jest zminimalizowanie wariancji długości słowa kodowego. Na przykład bufor komunikacyjny odbierający dane zakodowane przez Huffmana może wymagać większego rozmiaru, aby poradzić sobie ze szczególnie długimi symbolami, jeśli drzewo jest szczególnie niezrównoważone. Aby zminimalizować wariancję, po prostu zerwij wiązania między kolejkami, wybierając przedmiot w pierwszej kolejce. Ta modyfikacja zachowa matematyczną optymalność kodowania Huffmana, jednocześnie minimalizując wariancję i minimalizując długość najdłuższego kodu znakowego.
Dekompresja
Ogólnie rzecz biorąc, proces dekompresji polega po prostu na przetłumaczeniu strumienia kodów prefiksów na poszczególne wartości bajtów, zwykle poprzez przechodzenie przez węzeł drzewa Huffmana po węźle, gdy każdy bit jest odczytywany ze strumienia wejściowego (dotarcie do węzła liścia koniecznie kończy wyszukiwanie dla tej konkretnej wartości bajtu). Zanim jednak to nastąpi, trzeba w jakiś sposób zrekonstruować drzewo Huffmana. W najprostszym przypadku, w którym częstości znaków są dość przewidywalne, drzewo można wstępnie skonstruować (a nawet statystycznie skorygować w każdym cyklu kompresji), a tym samym ponownie użyć za każdym razem, kosztem przynajmniej pewnej miary wydajności kompresji. W przeciwnym razie informacja o rekonstrukcji drzewa musi zostać przesłana a priori. Naiwnym podejściem może być dodanie liczby częstotliwości każdego znaku do strumienia kompresji. Niestety narzut w takim przypadku może wynieść kilka kilobajtów, więc ta metoda ma mało praktycznego zastosowania. Jeśli dane są skompresowane przy użyciu kodowania kanonicznego , model kompresji można precyzyjnie zrekonstruować za pomocą tylko bitów informacji (gdzie jest liczba bitów na symbol). Inną metodą jest po prostu dodawanie drzewa Huffmana, krok po kroku, do strumienia wyjściowego. Na przykład, zakładając, że wartość 0 reprezentuje węzeł nadrzędny, a 1 węzeł-liść, za każdym razem, gdy ten ostatni zostanie napotkany, procedura budowania drzewa po prostu odczytuje następne 8 bitów, aby określić wartość znaku tego konkretnego liścia. Proces jest kontynuowany rekursywnie aż do osiągnięcia ostatniego węzła liścia; w tym momencie drzewo Huffmana zostanie w ten sposób wiernie zrekonstruowane. Narzut przy użyciu takiej metody waha się od około 2 do 320 bajtów (przy założeniu 8-bitowego alfabetu). Możliwych jest również wiele innych technik. W każdym razie, ponieważ skompresowane dane mogą zawierać nieużywane „bity końcowe”, dekompresor musi być w stanie określić, kiedy przestać generować dane wyjściowe. Można to osiągnąć albo przesyłając długość zdekompresowanych danych wraz z modelem kompresji, albo definiując specjalny symbol kodu oznaczający koniec wprowadzania danych (ta druga metoda może jednak niekorzystnie wpłynąć na optymalizację długości kodu).
Główne właściwości
Użyte prawdopodobieństwa mogą być prawdopodobieństwami ogólnymi dla domeny aplikacji, które są oparte na przeciętnym doświadczeniu, lub mogą być rzeczywistymi częstotliwościami znalezionymi w kompresowanym tekście. Wymaga to przechowywania tabeli częstotliwości ze skompresowanym tekstem. Zobacz sekcję Dekompresja powyżej, aby uzyskać więcej informacji o różnych technikach stosowanych w tym celu.
Optymalność
- Zobacz także kodowanie arytmetyczne # Kodowanie Huffmana
Oryginalny algorytm Huffmana jest optymalny dla kodowania symbol po symbolu ze znanym rozkładem prawdopodobieństwa wejściowego, tj. oddzielnego kodowania niepowiązanych symboli w takim strumieniu danych. Jednak nie jest to optymalne, gdy odrzuca się ograniczenie symbol po symbolu lub gdy funkcje masy prawdopodobieństwa są nieznane. Ponadto, jeśli symbole nie są niezależne i identycznie rozmieszczone , pojedynczy kod może być niewystarczający dla optymalności. Inne metody, takie jak kodowanie arytmetyczne, często mają lepsze możliwości kompresji.
Chociaż obie wyżej wymienione metody mogą łączyć dowolną liczbę symboli w celu bardziej wydajnego kodowania i ogólnie dostosowywać się do rzeczywistych statystyk wejściowych, kodowanie arytmetyczne robi to bez znacznego zwiększania złożoności obliczeniowej lub algorytmicznej (chociaż najprostsza wersja jest wolniejsza i bardziej złożona niż kodowanie Huffmana) . Taka elastyczność jest szczególnie przydatna, gdy prawdopodobieństwa wejściowe nie są dokładnie znane lub różnią się znacznie w strumieniu. Jednak kodowanie Huffmana jest zwykle szybsze, a kodowanie arytmetyczne było historycznie przedmiotem pewnych obaw związanych z kwestiami patentowymi . W związku z tym wiele technologii historycznie unikało kodowania arytmetycznego na rzecz Huffmana i innych technik kodowania przedrostkowego. Od połowy 2010 r. najczęściej stosowane techniki dla tej alternatywy dla kodowania Huffmana przeszły do domeny publicznej, gdy wygasły wczesne patenty.
Dla zbioru symboli o jednolitym rozkładzie prawdopodobieństwa i liczbie elementów, która jest potęgą dwójki , kodowanie Huffmana jest równoważne prostemu kodowaniu blokowemu binarnemu , np . kodowaniu ASCII . Odzwierciedla to fakt, że kompresja nie jest możliwa przy takich danych wejściowych, niezależnie od metody kompresji, tj. nie robienie nic z danymi jest optymalną rzeczą do zrobienia.
Kodowanie Huffmana jest optymalne spośród wszystkich metod w każdym przypadku, gdy każdy symbol wejściowy jest znaną niezależną i identycznie rozłożoną zmienną losową o prawdopodobieństwie dwójkowym . Kody przedrostkowe, a tym samym kodowanie Huffmana w szczególności, mają tendencję do nieefektywności w przypadku małych alfabetów, gdzie prawdopodobieństwa często mieszczą się między tymi optymalnymi (dwuadowymi) punktami. W najgorszym przypadku kodowania Huffmana może się zdarzyć, gdy prawdopodobieństwo najprawdopodobniej symbolu znacznie przekracza 2 -1 = 0,5, dzięki czemu górny limit nieefektywności nieograniczonego.
Istnieją dwa powiązane podejścia do obejścia tej konkretnej nieefektywności przy jednoczesnym korzystaniu z kodowania Huffmana. Łączenie ze sobą stałej liczby symboli („blokowanie”) często zwiększa (i nigdy nie zmniejsza) kompresji. Gdy rozmiar bloku zbliża się do nieskończoności, kodowanie Huffmana teoretycznie zbliża się do granicy entropii, tj. optymalnej kompresji. Jednak blokowanie dowolnie dużych grup symboli jest niepraktyczne, ponieważ złożoność kodu Huffmana jest liniowa pod względem liczby możliwości do zakodowania, a liczba ta jest wykładnicza w rozmiarze bloku. Ogranicza to ilość blokowania, która jest wykonywana w praktyce.
Praktyczną alternatywą, w powszechnym użyciu, jest kodowanie run-length . Ta technika dodaje jeden krok przed kodowaniem entropijnym, w szczególności zliczanie (przebiegów) powtarzających się symboli, które są następnie kodowane. Dla prostego przypadku procesów Bernoulliego , kod golomba jest optymalny spośród kodów prefiks kodowanie długości Uruchom, fakt udowodnione poprzez techniki kodowania Huffmana. Podobne podejście stosują faksy wykorzystujące zmodyfikowane kodowanie Huffmana . Jednak kodowanie run-length nie jest tak przystosowane do tak wielu typów danych wejściowych, jak inne technologie kompresji.
Wariacje
Istnieje wiele odmian kodowania Huffmana, z których niektóre wykorzystują algorytm podobny do Huffmana, a inne znajdują optymalne kody prefiksowe (na przykład nakładając różne ograniczenia na dane wyjściowe). Zauważ, że w tym drugim przypadku metoda nie musi być podobna do metody Huffmana, a nawet nie musi być nawet wielomianem .
n- ary kodowanie Huffmana
N -ary Huffman algorytm wykorzystuje {0, 1, ..., n - 1} alfabetu wiadomości kodowania i budować n -ary drzewo. To podejście zostało rozważone przez Huffmana w swoim oryginalnym artykule. Stosuje się ten sam algorytm, co w przypadku kodów binarnych ( n = 2), z tym wyjątkiem, że n najmniej prawdopodobnych symboli jest branych razem, a nie tylko 2 najmniej prawdopodobne. Zauważ, że dla n większych niż 2, nie wszystkie zestawy słów źródłowych mogą poprawnie utworzyć drzewo n- arne dla kodowania Huffmana. W takich przypadkach należy dodać dodatkowe miejsca z zerowym prawdopodobieństwem. Dzieje się tak, ponieważ drzewo musi tworzyć wykonawcę n do 1; w przypadku kodowania binarnego jest to kontrahent 2 do 1, a każdy zestaw może tworzyć takiego kontrahenta. Jeśli liczba słów źródłowych jest zgodna z 1 modulo n -1, to zbiór słów źródłowych utworzy właściwe drzewo Huffmana.
Adaptacyjne kodowanie Huffmana
Odmiana zwana adaptacyjnym kodowaniem Huffmana obejmuje dynamiczne obliczanie prawdopodobieństw na podstawie ostatnich rzeczywistych częstotliwości w sekwencji symboli źródłowych i zmianę struktury drzewa kodowania w celu dopasowania zaktualizowanych szacunków prawdopodobieństwa. Jest rzadko używany w praktyce, ponieważ koszt aktualizacji drzewa powoduje, że jest wolniejszy niż zoptymalizowane adaptacyjne kodowanie arytmetyczne , które jest bardziej elastyczne i ma lepszą kompresję.
Algorytm szablonu Huffmana
Najczęściej wagi używane w implementacjach kodowania Huffmana reprezentują prawdopodobieństwa liczbowe, ale algorytm podany powyżej nie wymaga tego; wymaga jedynie, aby wagi tworzyły całkowicie uporządkowany monoid przemienny , czyli sposób porządkowania wag i ich dodawania. Algorytm szablon Huffmana umożliwia on użyć dowolnego rodzaju ciężarków (koszty, częstotliwości par wag, masy nieliczbowa) i jedną z wielu metod łączących (nie tylko dodatek). Takie algorytmy mogą rozwiązywać inne problemy minimalizacji, takie jak minimalizacja , problem po raz pierwszy zastosowany do projektowania obwodów.
Kodowanie Huffmana o ograniczonej długości/minimalna wariancja Kodowanie Huffmana
Kodowanie Huffmana o ograniczonej długości jest wariantem, w którym celem jest nadal osiągnięcie minimalnej ważonej długości ścieżki, ale istnieje dodatkowe ograniczenie, że długość każdego słowa kodowego musi być mniejsza niż dana stała. Algorytm pakiet seryjnej rozwiązuje ten problem za pomocą prostego chciwy podejście bardzo podobnej do tej stosowanej przez algorytm Huffmana jest. Jego złożoność czasowa to , gdzie jest maksymalną długością słowa kodowego. Nie jest znany żaden algorytm rozwiązujący ten problem w czasie lub w czasie, w przeciwieństwie do odpowiednio wstępnie posortowanych i nieposortowanych konwencjonalnych problemów Huffmana.
Kodowanie Huffmana z nierównymi kosztami listów
W standardowym problemie kodowania Huffmana zakłada się, że każdy symbol w zbiorze, z którego zbudowane są słowa kodowe, ma równy koszt transmisji: słowo kodowe o długości N cyfr zawsze będzie miało koszt N , bez względu na to, ile z tych cyfr to 0, ile to jedynki itd. Przy takim założeniu minimalizacja całkowitego kosztu wiadomości i całkowita liczba cyfr to to samo.
Kodowanie Huffmana z nierównymi kosztami liter jest uogólnieniem bez tego założenia: litery alfabetu kodującego mogą mieć niejednolitą długość, ze względu na właściwości medium transmisyjnego. Przykładem jest kodowanie alfabetu Morse'a , gdzie „kreska” jest wysyłana dłużej niż „kropka”, a zatem koszt myślnika w czasie transmisji jest wyższy. Celem jest nadal minimalizacja średniej ważonej długości słowa kodowego, ale nie wystarczy już tylko zminimalizowanie liczby symboli wykorzystywanych w wiadomości. Nie jest znany żaden algorytm rozwiązujący to w ten sam sposób lub z taką samą wydajnością jak konwencjonalne kodowanie Huffmana, chociaż został on rozwiązany przez Karpa, którego rozwiązanie zostało udoskonalone dla przypadku kosztów całkowitych przez Golina .
Optymalne alfabetyczne drzewa binarne (kodowanie Hu-Tuckera)
W standardowym problemie kodowania Huffmana zakłada się, że dowolne słowo kodowe może odpowiadać dowolnemu symbolowi wejściowemu. W wersji alfabetycznej kolejność alfabetyczna wejść i wyjść musi być identyczna. Tak więc na przykład nie można przypisać code , ale zamiast tego należy przypisać albo lub . Ten jest również znany jako Hu-Tucker problemu, po TC Hu i Alan Tucker , autorzy referatu prezentujące pierwszy -Time rozwiązanie tego problemu optymalnego alfabetyczna binarny, który ma pewne podobieństwa do algorytmu Huffmana, ale nie jest odmianą ten algorytm. Później, metodę algorytm Garsia-Wachs z Adriano Garsia i Michelle Wachsa L. (1977), zastosowano prostszy układ logiczny do wykonywania tych samych porównanie w tym samym całkowity czas związany. Te optymalne alfabetyczne drzewa binarne są często używane jako binarne drzewa wyszukiwania .
Kanoniczny kodeks Huffmana
Jeśli wagi odpowiadające alfabetycznie uporządkowanym danym wejściowym są w kolejności numerycznej, kod Huffmana ma te same długości co optymalny kod alfabetyczny, który można znaleźć na podstawie obliczania tych długości, co sprawia, że kodowanie Hu-Tuckera jest niepotrzebne. Kod wynikający z numerycznie (prze)porządkowanych danych wejściowych jest czasami nazywany kanonicznym kodem Huffmana i często jest kodem używanym w praktyce, ze względu na łatwość kodowania/dekodowania. Technika znajdowania tego kodu jest czasami nazywana kodowaniem Huffmana-Shannona-Fano , ponieważ jest optymalna jak kodowanie Huffmana, ale alfabetyczna pod względem prawdopodobieństwa wagi, jak kodowanie Shannona-Fano . Odpowiadający przykładowi kod Huffmana–Shannona–Fano to , który mając takie same długości słowa kodowego jak rozwiązanie oryginalne, jest również optymalny. Ale w kanonicznym kodzie Huffmana rezultatem jest .
Aplikacje
Kodowanie arytmetyczne i kodowanie Huffmana dają równoważne wyniki — osiągając entropię — gdy każdy symbol ma prawdopodobieństwo postaci 1/2 k . W innych okolicznościach kodowanie arytmetyczne może oferować lepszą kompresję niż kodowanie Huffmana, ponieważ – intuicyjnie – jego „słowa kodowe” mogą mieć skutecznie niecałkowite długości bitów, podczas gdy słowa kodowe w kodach prefiksowych, takich jak kody Huffmana, mogą mieć tylko całkowitą liczbę bitów. Dlatego słowo kodowe o długości k tylko optymalnie pasuje do symbolu o prawdopodobieństwie 1/2 k, a inne prawdopodobieństwa nie są reprezentowane optymalnie; podczas gdy długość słowa kodowego w kodowaniu arytmetycznym może być dokładnie dopasowana do prawdziwego prawdopodobieństwa symbolu. Ta różnica jest szczególnie uderzająca w przypadku małych rozmiarów alfabetu.
Kody prefiksowe pozostają jednak w powszechnym użyciu ze względu na ich prostotę, dużą szybkość i brak ochrony patentowej . Są często używane jako „zaplecze” dla innych metod kompresji. Deflate ( algorytm PKZIP ) i kodeki multimedialne, takie jak JPEG i MP3, mają model front-end i kwantyzację, po której stosuje się kody prefiksów; są one często nazywane „kodami Huffmana”, mimo że większość aplikacji używa predefiniowanych kodów o zmiennej długości zamiast kodów zaprojektowanych przy użyciu algorytmu Huffmana.
Bibliografia
Bibliografia
- Thomas H. Cormen , Charles E. Leiserson , Ronald L. Rivest i Clifford Stein . Wprowadzenie do algorytmów , wydanie drugie. MIT Press i McGraw-Hill, 2001. ISBN 0-262-03293-7 . Sekcja 16.3, s. 385-392.






















![\max _{i}\left[w_{i}+\mathrm {długość} \left(c_{i}\right)\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a80c0b460cf854976824c251037db43d7ed1810)









