Geometria hiperboliczna - Hyperbolic geometry

Geometria
Wystające do sfery na płaszczyznę
Zarys Historia
Gałęzie Euklidesa Nieeuklidesowy Eliptyczny Kulisty Hiperboliczny Geometria niearchimedesowa Rzutowy Affine Syntetyczny Analityczny Algebraiczny Arytmetyka diofantyna Mechanizm różnicowy Riemanna Symplektyczny Dyskretna różnica Kompleks Skończone Dyskretny/Kombinatoryczny Cyfrowy Wypukły Obliczeniowa Fraktal Zakres
Koncepcje Cechy Wymiar Konstrukcje prostoliniowe i kompasowe Kąt Krzywa Przekątna Ortogonalność ( prostopadłość ) Równoległy Wierzchołek Stosowność Podobieństwo Symetria
Zerowymiarowy Punkt
Jednowymiarowy Linia człon promień Długość
Dwuwymiarowy Samolot Obszar Wielokąt Trójkąt Wysokość Przeciwprostokątna twierdzenie Pitagorasa Równoległobok Kwadrat Prostokąt Romb Romboid Czworoboczny trapez latawiec Koło Średnica Obwód Obszar
Trójwymiarowy Tom Sześcian prostopadłościan Cylinder Piramida Kula
Cztero- /inny wymiar Teserakt Hipersfera
Geometry
wg nazwy Aida Aryabhata Ahmes Alhazen Apoloniusz Archimedesa Atiyah Baudhayana Bolyai Brahmagupta Cartan Coxeter Kartezjusz Euklides Euler Gaus Gromow Hilbert Jyeṣṭhadewa Katjajanah Chajjam Klein Łobaczewski Manawa Minkowskiego Minggatu Pascal Pitagoras Parameśwara Poincaré Riemanna Sakabe Sijzi al-Tusi Veblen Virasena Yang Hui al-Yasamin Zhang Lista geometrii
przez okres p.n.e. Ahmes Baudhayana Manawa Pitagoras Euklides Archimedesa Apoloniusz 1-1400s Zhang Katjajanah Aryabhata Brahmagupta Virasena Alhazen Sijzi Chajjam al-Yasamin al-Tusi Yang Hui Parameśwara 1400-1700 Jyeṣṭhadewa Kartezjusz Pascal Minggatu Euler Sakabe Aida 1700-1900 Gaus Łobaczewski Bolyai Riemanna Klein Poincaré Hilbert Minkowskiego Cartan Veblen Coxeter Dzień dzisiejszy Atiyah Gromow
v T mi

W matematyce , geometria hiperboliczny (zwany również Lobachevskian geometrii lub Bolyai - Lobachevskian geometria ) jest nieeuklidesowa geometrii . Równolegle postulat od geometrii euklidesowej otrzymuje się:

Dla dowolnej danej linii R i punktu P nie na R , na płaszczyźnie zawierającej zarówno prostą R , jak i punkt P istnieją co najmniej dwie różne linie przechodzące przez P , które nie przecinają się z R .

(Porównaj z powyższego aksjomatu Playfaira za , nowoczesnej wersji Euclid „s równoległego postulatu ).

Hiperboliczna geometria płaska to również geometria powierzchni siodłowych i powierzchni pseudosferycznych , powierzchni o stałej ujemnej krzywiźnie Gaussa .

Współczesne zastosowanie geometrii hiperbolicznej znajduje się w szczególnej teorii względności , zwłaszcza w modelu Minkowskiego .

Kiedy geometrowie po raz pierwszy zdali sobie sprawę, że pracują z czymś innym niż standardowa geometria euklidesowa, opisali swoją geometrię pod wieloma różnymi nazwami; Felix Klein w końcu nadał tematowi nazwę geometria hiperboliczna, aby włączyć ją do rzadko obecnie używanej geometrii eliptycznej sekwencji ( geometria sferyczna ), geometrii parabolicznej ( geometria euklidesowa ) i geometrii hiperbolicznej. W byłym Związku Radzieckim jest powszechnie nazywana geometrią Łobaczewskiego, od nazwiska jednego z jej odkrywców, rosyjskiego geometra Nikołaja Łobaczewskiego .

Ta strona dotyczy głównie dwuwymiarowej (płaskiej) geometrii hiperbolicznej oraz różnic i podobieństw między geometrią euklidesową a hiperboliczną. Zobacz przestrzeń hiperboliczną, aby uzyskać więcej informacji na temat geometrii hiperbolicznej rozszerzonej do trzech i więcej wymiarów.

Nieruchomości

Związek z geometrią euklidesową

Geometria hiperboliczna jest ściślej związana z geometrią euklidesową, niż się wydaje: jedyną różnicą aksjomatyczną jest postulat równoległy . Kiedy postulat równoległy zostanie usunięty z geometrii euklidesowej, otrzymana geometria jest geometrią absolutną . Istnieją dwa rodzaje geometrii absolutnej, euklidesowa i hiperboliczna. Wszystkie twierdzenia geometrii absolutnej, w tym pierwszych 28 propozycji jednego księgowej Euklidesa Elementy , obowiązują w geometrii euklidesowej i hiperbolicznej. Zdania 27 i 28 Zarezerwuj jeden z Euklidesa Elementy udowodnić istnienie równoległych / non-przecinających się linii.

Ta różnica ma również wiele konsekwencji: pojęcia, które są równoważne w geometrii euklidesowej, nie są równoważne w geometrii hiperbolicznej; należy wprowadzić nowe koncepcje. Ponadto, ze względu na kąt równoległości , geometria hiperboliczna ma skalę bezwzględną , związek między pomiarami odległości i kąta.

Linie

Pojedyncze linie w geometrii hiperbolicznej mają dokładnie takie same właściwości jak pojedyncze linie proste w geometrii euklidesowej. Na przykład dwa punkty jednoznacznie definiują linię, a segmenty linii mogą być wydłużane w nieskończoność.

Dwie przecinające się linie mają takie same właściwości jak dwie przecinające się linie w geometrii euklidesowej. Na przykład dwie różne linie mogą przecinać się nie więcej niż w jednym punkcie, przecinające się linie tworzą równe przeciwne kąty, a sąsiednie kąty przecinających się linii są uzupełniające .

Po wprowadzeniu trzeciej linii mogą istnieć właściwości przecinających się prostych, które różnią się od przecinających się linii w geometrii euklidesowej. Na przykład, biorąc pod uwagę dwie przecinające się linie, istnieje nieskończenie wiele linii, które nie przecinają się z żadną z podanych linii.

Wszystkie te właściwości są niezależne od używanego modelu , nawet jeśli linie mogą wyglądać radykalnie inaczej.

Nieprzecinające się/równoległe linie

Nieprzecinające się linie w geometrii hiperbolicznej również mają właściwości, które różnią się od nieprzecinających się linii w geometrii euklidesowej :

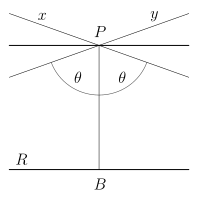
Dla każdej prostej R i dowolnego punktu P , który nie leży na R , na płaszczyźnie zawierającej prostą R i punkt P istnieją co najmniej dwie różne linie przechodzące przez P , które nie przecinają R .

Oznacza to, że przez P istnieje nieskończona liczba współpłaszczyznowych linii, które nie przecinają R .

Te nieprzecinające się linie są podzielone na dwie klasy:

• Dwie z linii ( x i y na schemacie) są graniczącymi równoleżnikami (czasami nazywanymi krytycznie równoległymi, horoparalelowymi lub po prostu równoległymi): jest jeden w kierunku każdego z idealnych punktów na „końcach” R , asymptotycznie zbliżający się do R , zawsze zbliżając się do R , ale nigdy go nie spotykając.
• Wszystkie inne nieprzecinające się linie mają punkt o minimalnej odległości i rozchodzą się z obu stron tego punktu i są nazywane ultrarównoległymi , rozbieżnymi równoległymi lub czasami nie przecinającymi się.

Niektóre geometry po prostu używają wyrażenia „ linie równoległe ” w znaczeniu „ ograniczające linie równoległe ”, przy czym linie ultrarównoległe oznaczają po prostu nieprzecinające się .

Te graniczne równoleżniki tworzą kąt θ z PB ; kąt ten zależy tylko od krzywizny Gaussa płaszczyzny i odległości PB i nazywany jest kątem równoległości .

W przypadku linii ultrarównoległych twierdzenie ultrarównoległe mówi, że w płaszczyźnie hiperbolicznej istnieje unikalna linia, która jest prostopadła do każdej pary linii ultrarównoległych.

Koła i dyski

W geometrii hiperbolicznej obwód okręgu o promieniu r jest większy niż . ${\displaystyle 2\pi r}$

Niech , gdzie jest krzywizna Gaussa płaszczyzny. W geometrii hiperbolicznej jest ujemna, więc pierwiastek kwadratowy jest liczbą dodatnią. ${\ Displaystyle R = {\ Frac {1} {\ sqrt {-K}}}}$${\ Displaystyle K}$${\ Displaystyle K}$

Wtedy obwód okręgu o promieniu r jest równy:

${\ Displaystyle 2 \ pi R \ sinh {\ Frac {R} {R}} \,.}$

A obszar załączonego dysku to:

${\ Displaystyle 4 \ pi R ^ {2} \ sinh ^ {2} {\ Frac {R} {2 R}} = 2 \ pi R ^ {2} \ lewo (\ cosh {\ Frac {r} {R} }-1\prawo)\,.}$

Dlatego w geometrii hiperbolicznej stosunek obwodu okręgu do jego promienia jest zawsze ściśle większy niż , chociaż można go dowolnie przybliżyć, wybierając wystarczająco mały okrąg. ${\displaystyle 2\pi}$

Jeśli krzywizna Gaussa płaszczyzny wynosi -1, to krzywizna geodezyjna okręgu o promieniu r wynosi:${\displaystyle {\frac {1}{\tanh(r)}}}$

Hipercykle i horocykle

W geometrii hiperbolicznej nie ma linii, której wszystkie punkty są równoodległe od innej linii. Zamiast tego punkty, które mają tę samą odległość ortogonalną od danej linii, leżą na krzywej zwanej hipercyklem .

Inną specjalną krzywą jest horocykl , krzywa, której normalne promienie ( linie prostopadłe ) są ograniczone równolegle do siebie (wszystkie zbiegają się asymptotycznie w jednym kierunku do tego samego idealnego punktu , środka horocykla).

Przez każdą parę punktów znajdują się dwa horocykle. Centrach horocycles są idealne punkty z symetralnej tego odcinka linii między nimi.

Biorąc pod uwagę wszystkie trzy główne punkty, wszystkie one leżą na jednej linii, hypercycle , horocycle lub okręgu.

Długość linii segmentu to najkrótsza odległość między dwoma punktami. Długość łuku hipercyklu łączącego dwa punkty jest dłuższa niż odcinka linii i krótsza niż w przypadku horocykla, łączącego te same dwa punkty. Długość łuku obu horocykli łączących dwa punkty są równe. Długość łuku okręgu między dwoma punktami jest większa niż długość łuku horocykla łączącego dwa punkty.

Jeśli krzywizna Gaussa płaszczyzny wynosi -1, to krzywizna geodezyjna horocykla wynosi 1, a hipercyklu wynosi od 0 do 1.

Trójkąty

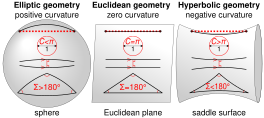
W przeciwieństwie do trójkątów euklidesowych, gdzie kąty zawsze sumują się do π radianów (180°, kąt prosty ), w geometrii hiperbolicznej suma kątów trójkąta hiperbolicznego jest zawsze ściśle mniejsza niż π radianów (180°, kąt prosty ). Różnicę nazywamy wadą .

Pole trójkąta hiperbolicznego to jego defekt w radianach pomnożony przez R ² . W konsekwencji wszystkie trójkąty hiperboliczne mają obszar mniejszy lub równy R ² π. Pole hiperbolicznego trójkąta idealnego, w którym wszystkie trzy kąty wynoszą 0°, jest równe temu maksimum.

Podobnie jak w geometrii euklidesowej , każdy trójkąt hiperboliczny ma koło . W geometrii hiperbolicznej, jeśli wszystkie trzy jego wierzchołki leżą na horocycle lub hypercycle , wtedy trójkąt ma ograniczony krąg .

Podobnie jak w geometrii sferycznej i eliptycznej , w geometrii hiperbolicznej, jeśli dwa trójkąty są podobne, muszą być przystające.

Zwykły apeirogon

Specjalnym wielokątem w geometrii hiperbolicznej jest apeirogon foremny , wielokąt jednorodny o nieskończonej liczbie boków.

W geometrii euklidesowej jedynym sposobem na skonstruowanie takiego wielokąta jest sprawienie, by długość boków miała tendencję do zera, a apeirogon jest nie do odróżnienia od okręgu, lub aby kąty wewnętrzne miały tendencję do 180 stopni, a apeirogon zbliżał się do linii prostej.

Jednak w geometrii hiperbolicznej apeirogon foremny ma boki dowolnej długości (tzn. pozostaje wielokątem).

Dwusieczne boczne i kątowe będą, w zależności od długości boku i kąta między bokami, ograniczające lub rozchodzące się równolegle (patrz linie powyżej ). Jeśli dwusieczne są ograniczone równolegle, apeirogon można wpisać i opisać koncentrycznymi horocyklami .

Jeśli dwusieczne rozchodzą się równolegle, pseudogon (wyraźnie różny od apeirogonu) może być wpisany w hipercykle (wszystkie wierzchołki znajdują się w tej samej odległości od linii, osi, a także punktu środkowego segmentów bocznych są w równej odległości od tej samej osi. )

Parkietaże

Podobnie jak płaszczyzna euklidesowa, możliwe jest również mozaikowanie płaszczyzny hiperbolicznej wielokątami foremnymi jako ścianami .

Istnieje nieskończona liczba jednorodnych kafelków opartych na trójkątach Schwarza ( p q r ), gdzie 1/ p + 1/ q + 1/ r < 1, gdzie p ,  q ,  r są rzędami symetrii odbicia w trzech punktach fundamentalny trójkąt domeny , grupa symetrii jest grupą trójkąta hiperbolicznego . Istnieje również nieskończenie wiele jednolitych kafelków, których nie można wygenerować z trójkątów Schwarza, niektóre na przykład wymagają czworokątów jako domen podstawowych.

Znormalizowana krzywizna Gaussa

Chociaż geometria hiperboliczna ma zastosowanie do każdej powierzchni o stałej ujemnej krzywiźnie Gaussa , zwykle przyjmuje się skalę, w której krzywizna K wynosi -1.

Powoduje to, że niektóre formuły stają się prostsze. Oto kilka przykładów:

• Pole trójkąta jest równe jego defektowi kątowemu w radianach .
• Powierzchnia sektora horocyklicznego jest równa długości jego łuku horocyklicznego.
• Łuk horocykla , w którym linia styczna w jednym punkcie końcowym jest ograniczona równolegle do promienia przechodzącego przez drugi punkt końcowy, ma długość 1.
• Stosunek długości łuku między dwoma promieniami dwóch koncentrycznych horocykli, w których horocykle są oddalone od siebie o 1, wynosi e  : 1.

Kartezjańskie układy współrzędnych

W geometrii hiperbolicznej suma kątów czworokąta jest zawsze mniejsza niż 360 stopni, a prostokąty hiperboliczne różnią się znacznie od prostokątów euklidesowych, ponieważ nie ma linii równoodległych, więc właściwy prostokąt euklidesowy musiałby być otoczony dwiema liniami i dwoma hipercyklami . To wszystko komplikuje układy współrzędnych.

Istnieją jednak różne układy współrzędnych dla geometrii płaszczyzny hiperbolicznej. Wszystkie opierają się na wybraniu punktu (początku) na wybranej prostej skierowanej ( oś x ), a następnie istnieje wiele możliwości wyboru.

Współrzędne Łobaczewskiego x i y są znajdowane przez upuszczenie prostopadłej na oś x . x będzie etykietą stopy prostopadłej. y będzie odległością wzdłuż prostopadłej danego punktu od jego stopy (dodatnia z jednej strony i ujemna z drugiej).

Inny układ współrzędnych mierzy odległość od punktu do horocyklu przez punkt początkowy wyśrodkowany wokół i długość wzdłuż tego horocyklu. ${\displaystyle (0,+\infty)}$

Inne układy współrzędnych używają modelu Kleina lub modelu dysku Poincare opisanego poniżej i przyjmują współrzędne euklidesowe jako hiperboliczne.

Dystans

Skonstruuj kartezjański układ współrzędnych w następujący sposób. Wybierz linię ( oś x ) w płaszczyźnie hiperbolicznej (ze standaryzowaną krzywizną -1) i oznacz punkty na niej przez ich odległość od punktu początkowego ( x = 0) na osi x (dodatnie z jednej strony i negatywne z drugiej). Dla dowolnego punktu na płaszczyźnie można zdefiniować współrzędne x i y przez upuszczenie prostopadłej na oś x . x będzie etykietą stopy prostopadłej. y będzie odległością wzdłuż prostopadłej danego punktu od jego stopy (dodatnia z jednej strony i ujemna z drugiej). Wtedy odległość między dwoma takimi punktami będzie

${\ Displaystyle \ operatorname {odleg.} (\ langle x_ {1}, Y_ {1} \ rangle, \ langle x_ {2}, y_ {2} \ rangle ) = \ operatorname {arcosh} \ lewo (\ cosh y_ { 1}\cosh(x_{2}-x_{1})\cosh y_{2}-\sinh y_{1}\sinh y_{2}\right)\,.}$

Ten wzór można wyprowadzić ze wzorów dotyczących trójkątów hiperbolicznych .

Odpowiednim tensorem metryki jest: . ${\ Displaystyle (\ operatorname {d} s) ^ {2} = \ cosh ^ {2} r \ (\ operatorname {d} x) ^ {2} + (\ operatorname {d} r) ^ {2} }$

W tym układzie współrzędnych linie proste są albo prostopadłe do osi x (z równaniem x = stała) albo opisane równaniami postaci

${\ Displaystyle \ tanh y = A \ cosh x + B \ sinh x \ quad {\ tekst {kiedy}} \ quad A ^ {2} <1 + B ^ {2}}$

gdzie A i B są rzeczywistymi parametrami charakteryzującymi linię prostą.

Historia

Od czasu opublikowania Elementów Euklidesa około 300 roku p.n.e. wielu geometrów próbowało udowodnić postulat równoległości . Niektórzy próbowali to udowodnić, zakładając jej negację i próbując wyprowadzić sprzeczność . Przede wszystkim wśród nich były Proklos , Ibn al-Haytham (Alhacen), Omar Chajjam , Nasir ad-Din Tusi , Witelo , Gersonides , Alfonso , a później Giovanni Girolamo Saccheriego , John Wallis , Johann Heinrich Lambert i Legendre . Ich próby były skazane na niepowodzenie (jak już wiemy, postulatu równoległego nie da się udowodnić z innych postulatów), ale ich wysiłki doprowadziły do ​​odkrycia geometrii hiperbolicznej.

Twierdzenia Alhacena, Khayyama i al-Tūsī na czworokątach , w tym czworokąt Ibn al-Haythama-Lamberta i czworokąt Khayyam-Saccheri , były pierwszymi twierdzeniami o geometrii hiperbolicznej. Ich prace nad geometrią hiperboliczną miały znaczący wpływ na jej rozwój wśród późniejszych europejskich geometrów, m.in. Witelo, Gersonidesa, Alfonsa, Johna Wallisa i Saccheriego.

W XVIII wieku Johann Heinrich Lambert wprowadził funkcje hiperboliczne i obliczył pole trójkąta hiperbolicznego .

Rozwój XIX-wieczny

W XIX wieku geometria hiperboliczna była intensywnie badana przez Nikołaja Iwanowicza Łobaczewskiego , Jánosa Bolyai , Carla Friedricha Gaussa i Franza Taurinusa . W przeciwieństwie do swoich poprzedników, którzy chcieli jedynie wyeliminować równoległy postulat z aksjomatów geometrii euklidesowej, autorzy ci zdali sobie sprawę, że odkryli nową geometrię. Gauss napisał w liście do Franza Taurinusa z 1824 roku, że to on go skonstruował, ale Gauss nie opublikował swojej pracy. Gauss nazwał to „ geometrią nieeuklidesową ”, co spowodowało, że kilku współczesnych autorów nadal uważało „geometrię nieeuklidesową” i „geometrię hiperboliczną” za synonimy. Taurinus opublikował wyniki dotyczące trygonometrii hiperbolicznej w 1826 roku, argumentując, że geometria hiperboliczna jest wewnętrznie spójna, ale nadal wierzył w szczególną rolę geometrii euklidesowej. Kompletny system geometrii hiperbolicznej został opublikowany przez Łobaczewskiego w 1829/1830, podczas gdy Bolyai odkrył go niezależnie i opublikował w 1832 roku.

W 1868 Eugenio Beltrami dostarczył modele (patrz niżej) geometrii hiperbolicznej i wykorzystał to do udowodnienia, że ​​geometria hiperboliczna była spójna wtedy i tylko wtedy, gdy była to geometria euklidesowa.

Termin „geometria hiperboliczna” został wprowadzony przez Felixa Kleina w 1871 roku. Klein podążył za inicjatywą Arthura Cayleya, aby wykorzystać transformacje geometrii rzutowej do wytworzenia izometrii . Pomysł wykorzystywał przekrój stożkowy lub kwadratowy do zdefiniowania regionu i stosował współczynnik krzyżowy do zdefiniowania metryki . Transformacje rzutowe, które opuszczają sekcję stożkową lub stabilną kwadratową, to izometrie. „Klein wykazał, że jeśli absolut Cayleya jest prawdziwą krzywą, to część płaszczyzny rzutowej w jej wnętrzu jest izometryczna względem płaszczyzny hiperbolicznej…”

Więcej informacji na ten temat można znaleźć w artykule o geometrii nieeuklidesowej oraz w odnośnikach Coxeter i Milnor .

Konsekwencje filozoficzne

Odkrycie geometrii hiperbolicznej miało ważne konsekwencje filozoficzne . Przed jej odkryciem wielu filozofów (m.in. Hobbes i Spinoza ) postrzegało rygor filozoficzny w kategoriach „metody geometrycznej”, nawiązując do metody rozumowania zastosowanej w Elementach Euklidesa .

Kant w Krytyce czystego rozumu doszedł do wniosku, że przestrzeń (w geometrii euklidesowej ) i czas nie są przez człowieka odkrywane jako obiektywne cechy świata, ale są częścią nieuniknionej systematycznej struktury organizowania naszych doświadczeń.

Mówi się, że Gauss nie opublikował niczego na temat geometrii hiperbolicznej ze strachu przed „wrzawą Beotian ”, co zrujnowałoby jego status princepsa mathematicorum (łac. „Książę Matematyków”). „Wrzawa Beotian” pojawiała się i odchodziła, dając impuls do wielkich ulepszeń w zakresie matematycznego rygoru , analitycznej filozofii i logiki . Geometria hiperboliczna okazała się w końcu spójna i dlatego jest kolejną prawidłową geometrią.

Geometria wszechświata (tylko wymiary przestrzenne)

Ponieważ geometria euklidesowa, hiperboliczna i eliptyczna są spójne, powstaje pytanie: jaka jest rzeczywista geometria przestrzeni, a jeśli jest hiperboliczna czy eliptyczna, jaka jest jej krzywizna?

Lobachevsky już próbowali zmierzyć krzywiznę wszechświata poprzez pomiar paralaksy z Syriuszem i leczenia Syriusza jako punkt ideał kątem równoległości . Zdał sobie sprawę, że jego pomiary nie były wystarczająco precyzyjne, aby dać jednoznaczną odpowiedź, ale doszedł do wniosku, że jeśli geometria wszechświata jest hiperboliczna, to długość bezwzględna jest co najmniej milion razy większa od średnicy orbity Ziemi (2 000 000  AU , 10 parsek ). Niektórzy twierdzą, że jego pomiary były metodologicznie błędne.

Henri Poincaré w swoim eksperymencie myślowym ze światem kuli doszedł do wniosku, że codzienne doświadczenie niekoniecznie wyklucza inne geometrie.

Geometryzacja przypuszczenie daje pełną listę ośmiu możliwości podstawowej geometrii naszej przestrzeni. Problem z ustaleniem, który z nich ma zastosowanie, polega na tym, że aby uzyskać ostateczną odpowiedź, musimy być w stanie przyjrzeć się ekstremalnie dużym kształtom – znacznie większym niż cokolwiek na Ziemi, a może nawet w naszej galaktyce.

Geometria wszechświata (szczególna teoria względności)

Szczególna teoria względności stawia przestrzeń i czas na równi, tak że zamiast rozpatrywać przestrzeń i czas oddzielnie, rozważa się geometrię zunifikowanej czasoprzestrzeni . Geometria Minkowskiego zastępuje geometrię Galileusza (która jest trójwymiarową przestrzenią euklidesową z czasem względności Galileusza ).

W teorii względności, a nie rozważa euklidesowej geometrii eliptyczne i hiperboliczne, odpowiednie geometrie do rozważenia są Czasoprzestrzeń Minkowskiego , de Sitter przestrzeń i anty-de Sitter przestrzeni , odpowiadającej zera, dodatnia i ujemna krzywizna odpowiednio.

Geometria hiperboliczna wchodzi w szczególną teorię względności dzięki szybkości , która zastępuje prędkość i jest wyrażona przez kąt hiperboliczny . Badanie tej geometrii prędkości zostało nazwane geometrią kinematyczną . Przestrzeń prędkości relatywistycznych ma trójwymiarową geometrię hiperboliczną, w której funkcję odległości wyznacza się z prędkości względnych „pobliskich” punktów (prędkości).

Fizyczne realizacje płaszczyzny hiperbolicznej

Płaszczyzna hiperboliczna to płaszczyzna, w której każdy punkt jest punktem siodłowym . W przestrzeni euklidesowej istnieją różne pseudosfery, które mają skończony obszar o stałej ujemnej krzywiźnie Gaussa.

Według twierdzenia Hilberta nie jest możliwe izometryczne zanurzenie kompletnej płaszczyzny hiperbolicznej (całkowitej regularnej powierzchni o stałej ujemnej krzywiźnie Gaussa ) w trójwymiarowej przestrzeni euklidesowej.

Inne użyteczne modele geometrii hiperbolicznej istnieją w przestrzeni euklidesowej, w której metryka nie jest zachowana. Szczególnie dobrze znany papierowy model oparty na pseudosferze zawdzięczamy Williamowi Thurstonowi .

Sztuka szydełkowania została wykorzystana (patrz Matematyka i sztuki włókiennicze § Dzianie i szydełkowanie ) do zademonstrowania płaszczyzn hiperbolicznych, pierwszy taki pokaz został wykonany przez Dainę Taimiņa .

W 2000 r. Keith Henderson zademonstrował szybki do wykonania papierowy model, nazwany „ hiperboliczną piłką nożną ” (dokładniej, obcięty trójkątny układ 7 ).

Instrukcję wykonania kołdry hiperbolicznej, zaprojektowaną przez Helamana Fergusona , udostępnił Jeff Weeks .

Modele płaszczyzny hiperbolicznej

Istnieją różne powierzchnie pseudosferyczne , które na dużym obszarze mają stałą ujemną krzywiznę Gaussa, z których najlepiej znana jest pseudosfera .

Ale łatwiej jest zrobić geometrię hiperboliczną na innych modelach.

Dostępne są cztery modele powszechnie stosowane do geometrii hiperbolicznej: the modelu Klein The modelu dysku Poincaré The pół-plane modelu Poincaré i Lorentza lub hiperboloida modelu . Modele te definiują płaszczyznę hiperboliczną, która spełnia aksjomaty geometrii hiperbolicznej. Pomimo swoich nazw, pierwsze trzy wymienione powyżej jako modele przestrzeni hiperbolicznej wprowadził Beltrami , a nie Poincaré czy Klein . Wszystkie te modele można rozszerzyć do większej liczby wymiarów.

Model Beltramiego-Kleina

Model Beltramiego-Kleina , znany również jako rzutowy model dysku, model dysku Kleina i model Kleina , nosi imię Eugenio Beltramiego i Felixa Kleina .

Dla dwóch wymiarów model ten wykorzystuje wnętrze okręgu jednostkowego dla pełnej płaszczyzny hiperbolicznej , a cięciwy tego okręgu są liniami hiperbolicznymi.

Dla wyższych wymiarów model ten wykorzystuje wnętrze jednostki ball , a akordy tej n- ball są liniami hiperbolicznymi.

• Model ten ma tę zaletę, że linie są proste, ale wadę, że kąty są zniekształcone (odwzorowanie nie jest konforemne ), a koła nie są przedstawiane jako koła.
• Odległość w tym modelu to połowa logarytmu współczynnika krzyżowego , który został wprowadzony przez Arthura Cayleya w geometrii rzutowej .

Model dysku Poincare

Model dysku Poincaré , znany również jako model dysku konforemnego, również wykorzystuje wnętrze okręgu jednostkowego , ale linie są reprezentowane przez łuki okręgów, które są prostopadłe do okręgu granicznego, plus średnice okręgu granicznego.

• Model ten zachowuje kąty, dzięki czemu jest konformalny . Wszystkie izometrie w tym modelu są zatem transformacjami Möbiusa .
• Okręgi całkowicie wewnątrz dysku pozostają okręgami, chociaż euklidesowy środek okręgu jest bliżej środka dysku niż hiperboliczny środek okręgu.
• Horocykle to okręgi w obrębie dysku, które są styczne do okręgu granicznego, minus punkt kontaktu.
• Hipercykle to otwarte cięciwy i łuki kołowe w obrębie dysku, które kończą się na okręgu granicznym pod kątami innymi niż ortogonalne.

Model półpłaszczyzny Poincaré

Model półpłaszczyznowy Poincarégo przyjmuje połowę płaszczyzny euklidesowej, ograniczoną linią B płaszczyzny, jako model płaszczyzny hiperbolicznej. Linia B nie jest uwzględniona w modelu.

Płaszczyzna euklidesowa może być traktowana jako płaszczyzna o kartezjańskim układzie współrzędnych, a oś x jest traktowana jako linia B, a półpłaszczyzna jest górną połówką ( y > 0) tej płaszczyzny.

• Linie hiperboliczne są wtedy albo półokręgami prostopadłymi do B, albo promieniami prostopadłymi do B .
• Długość przedziału na promieniu jest podana za pomocą miary logarytmicznej, więc jest niezmienna w przekształceniu homotetycznym ${\ Displaystyle (x, y) \ mapsto (x \ lambda r) \ quad \ lambda > 0.}$
• Podobnie jak model dysku Poincarégo, ten model zachowuje kąty, a zatem jest konforemny . Wszystkie izometrie w tym modelu są zatem transformacjami Möbiusa płaszczyzny.
• Model półpłaszczyznowy jest granicą modelu dysku Poincarégo, którego granica jest styczna do B w tym samym punkcie, podczas gdy promień modelu dysku sięga nieskończoności.

Model hiperboloidy

Model hiperboloidy lub model Lorentza wykorzystuje dwuwymiarową hiperboloidę obrotu (dwóch arkuszy, ale wykorzystującą jedną) osadzoną w trójwymiarowej przestrzeni Minkowskiego . Ten model jest ogólnie przypisywany Poincaré, ale Reynolds mówi, że Wilhelm Killing używał tego modelu w 1885 roku

• Model ten ma bezpośrednie zastosowanie do szczególnej teorii względności , ponieważ 3-przestrzeń Minkowskiego jest modelem czasoprzestrzeni , tłumiącym jeden wymiar przestrzenny. Hiperboloidę można przyjąć do reprezentowania zdarzeń, do których w ustalonym odpowiednim czasie dotrą różni obserwatorzy poruszający się promieniście w płaszczyźnie przestrzennej z jednego punktu .
• Hiperboliczną odległość między dwoma punktami na hiperboloidzie można następnie zidentyfikować ze względną szybkością między dwoma odpowiednimi obserwatorami.
• Model uogólnia bezpośrednio do dodatkowego wymiaru, gdzie trójwymiarowa geometria hiperboliczna odnosi się do 4-przestrzeni Minkowskiego.

Model półkuli

Model półkuli nie jest często używany jako sam model, ale działa jako przydatne narzędzie do wizualizacji przekształceń między innymi modelami.

Model półkuli wykorzystuje górną połowę sfery jednostkowej : ${\displaystyle x^{2}+y^{2}+z^{2}=1,z>0.}$

Linie hiperboliczne to półkola prostopadłe do granicy półkuli.

Model półkuli jest częścią sfery Riemanna , a różne rzuty dają różne modele płaszczyzny hiperbolicznej:

• Rzut stereograficzny z na płaszczyznę rzutuje odpowiadające punkty na modelu dysku Poincarégo${\ Displaystyle (0,0,-1)}$${\ Displaystyle z = 0}$
• Rzut stereograficzny z powierzchni rzutuje odpowiadające punkty na modelu hiperboloidy${\ Displaystyle (0,0,-1)}$${\ Displaystyle x ^ {2} + ^ {2}-z ^ {2} = -1, z > 0}$
• Rzut stereograficzny z na płaszczyznę rzutuje odpowiadające punkty na modelu półpłaszczyznowym Poincarégo${\ Displaystyle (-1,0,0)}$${\displaystyle x=1}$
• Rzut prostopadły na płaszczyznę rzutuje odpowiadające punkty na modelu Beltramiego-Kleina .${\ Displaystyle Z = C}$
• Rzut centralny ze środka kuli na płaszczyznę rzutuje odpowiadające punkty na Modelu Gansa${\displaystyle z=1}$

Zobacz dalej: Połączenie między modelami (poniżej)

Model Gansa

W 1966 David Gans zaproponował spłaszczony model hiperboloidy w czasopiśmie American Mathematical Monthly . Jest to odwzorowanie ortogonalne modelu hiperboloidu na płaszczyznę xy. Model ten nie jest tak szeroko stosowany jak inne modele, ale mimo to jest całkiem przydatny w zrozumieniu geometrii hiperbolicznej.

• W przeciwieństwie do modeli Kleina czy Poincaré, ten model wykorzystuje całą płaszczyznę euklidesową .
• Linie w tym modelu są reprezentowane jako gałęzie hiperboli .

Model zespołu

Model pasmowy wykorzystuje część płaszczyzny euklidesowej pomiędzy dwiema równoległymi liniami. Odległość jest zachowana wzdłuż jednej linii przez środek pasma. Zakładając, że pasmo jest podane przez , metryka jest podana przez . ${\ Displaystyle \ {z \ w \ mathbb {C}: | \ operatorname {im} z | <\ pi /2 \}}$${\ Displaystyle | dz | \ s (\ nazwa operatora {im} z)}$

Połączenie między modelami

Modele krążka Poincarégo, hemisferycznego i hiperboloidowego są powiązane projekcją stereograficzną od -1. Model Beltramiego-Kleina jest rzutem prostokątnym z modelu półkulistego. Model półpłaszczyznowy Poincarégo tutaj odwzorowywany z modelu półkulistego przez promienie z lewego końca modelu dysku Poincarégo.

Wszystkie modele zasadniczo opisują tę samą strukturę. Różnica między nimi polega na tym, że reprezentują różne wykresy współrzędnych ułożone w tej samej przestrzeni metrycznej , czyli płaszczyźnie hiperbolicznej. Cechą charakterystyczną samej płaszczyzny hiperbolicznej jest to, że ma ona stałą ujemną krzywiznę Gaussa , która jest obojętna na używany wykres współrzędnych. W geodezyjne są podobnie niezmienna: to znaczy, geodezyjne mapa do transformacji współrzędnych geodezyjnych poniżej. Geometria hiperboliczna jest ogólnie wprowadzana w kategoriach geodezji i ich przecięć na płaszczyźnie hiperbolicznej.

Gdy już wybierzemy wykres współrzędnych (jeden z „modeli”), zawsze możemy osadzić go w przestrzeni euklidesowej o tym samym wymiarze, ale osadzanie wyraźnie nie jest izometryczne (ponieważ krzywizna przestrzeni euklidesowej wynosi 0). Przestrzeń hiperboliczna może być reprezentowana przez nieskończenie wiele różnych wykresów; ale zanurzenia w przestrzeni euklidesowej wynikające z tych czterech konkretnych wykresów wykazują pewne interesujące cechy.

Ponieważ cztery modele opisują tę samą przestrzeń metryczną, każdy z nich można przekształcić w drugi.

Zobacz na przykład:

• relacja modelu Beltramiego-Kleina do modelu hiperboloidowego ,
• relacja modelu Beltramiego-Kleina do modelu dysku Poincarégo ,
• oraz stosunek modelu dysku Poincarégo do modelu hiperboloidowego .

Izometrie płaszczyzny hiperbolicznej

Każda izometria ( przekształcenie lub ruch ) płaszczyzny hiperbolicznej może być zrealizowana jako kompozycja co najwyżej trzech odbić . W n- wymiarowej przestrzeni hiperbolicznej może być wymaganych do n +1 odbić. (Dotyczy to również geometrii euklidesowych i sferycznych, ale poniższa klasyfikacja jest inna.)

Wszystkie izometrie płaszczyzny hiperbolicznej można podzielić na następujące klasy:

• Zachowanie orientacji
  • isometry tożsamość - porusza się nic; zero odbić; zero stopni swobody .
  • inwersja przez punkt (pół obrotu) — dwa odbicia po prostopadłych do siebie prostych przechodzących przez dany punkt, czyli obrót o 180 stopni wokół punktu; dwa stopnie swobody .
  • obrót wokół punktu normalnego — dwa odbicia od linii przechodzących przez dany punkt (w specjalnym przypadku inwersja); punkty poruszają się po okręgach wokół środka; trzy stopnie swobody.
  • „obrót” wokół punktu idealnego (horolation) — dwa odbicia przez linie prowadzące do punktu idealnego; punkty poruszają się po horocyklach, których środek znajduje się w idealnym punkcie; dwa stopnie swobody.
  • translacja po linii prostej — dwa odbicia przez linie prostopadłe do danej linii; punkty poza daną linią poruszają się po hipercyklach; trzy stopnie swobody.
• Odwracanie orientacji
  • odbicie przez linię — jedno odbicie; dwa stopnie swobody.
  • połączone odbicie przez linię i translację wzdłuż tej samej linii — dojazd do refleksji i translacji; wymagane trzy odbicia; trzy stopnie swobody.

Geometria hiperboliczna w sztuce

Słynne ryciny MC Eschera Circle Limit III i Circle Limit IV dość dobrze ilustrują model konforemnego dysku ( model dysku Poincarégo ). Białe linie w III nie są do końca geodezyjne (są hipercyklami ), ale są do nich bliskie. Można też całkiem wyraźnie zobaczyć ujemną krzywiznę płaszczyzny hiperbolicznej, poprzez jej wpływ na sumę kątów w trójkątach i kwadratach.

Na przykład w Circle Limit III każdy wierzchołek należy do trzech trójkątów i trzech kwadratów. Na płaszczyźnie euklidesowej ich kąty sumują się do 450°; czyli koło i ćwiartka. Z tego widzimy, że suma kątów trójkąta w płaszczyźnie hiperbolicznej musi być mniejsza niż 180°. Inną widoczną właściwością jest wzrost wykładniczy . Na przykład w Circle Limit III widać, że liczba ryb w odległości n od środka rośnie wykładniczo. Ryby mają równy obszar hiperboliczny, więc pole kuli o promieniu n musi rosnąć wykładniczo w n .

Sztuka szydełka ma zostały wykorzystane do wykazania hiperboliczne samolotów (na zdjęciu powyżej) z pierwszego podejmowane przez Daina Taimiņa , którego książka Szydełkowanie Przygody z Planes hiperboliczny wygrał 2009 Księgarz / Diagram Prize dla najdziwniejszych tytułów Roku .

HyperRogue to gra typu roguelike, której akcja toczy się na różnych płaszczyznach płaszczyzny hiperbolicznej .

Wyższe wymiary

Geometria hiperboliczna nie jest ograniczona do 2 wymiarów; geometria hiperboliczna istnieje dla każdej większej liczby wymiarów.

Jednorodna struktura

Przestrzeń hiperboliczna wymiaru n jest szczególnym przypadkiem riemannowskiej symetrycznej przestrzeni typu niezwartego, ponieważ jest izomorficzna do ilorazu

${\ Displaystyle \ operatorname {O} (1, n) / (\ operatorname {O} (1) \ razy \ operatorname {O} (n)).}$

Grupa ortogonalna O(1, n ) działa poprzez przekształcenia zachowujące normę na przestrzeni Minkowskiego R ^{1, n} i działa przechodnie na dwuarkuszowej hiperboloidzie wektorów normy 1. Linie czasopodobne (tzn. te z dodatnimi stycznymi o normie dodatniej) przechodzące przez punkt początkowy przechodzą przez punkty antypodalne w hiperboloidzie, więc przestrzeń takich linii daje model hiperbolicznej n -przestrzeni. Stabilizator od jakiejkolwiek linii jest izomorficzny w produkcie ortogonalnego grupy O ( n ) oraz O (1), przy czym O ( n ) występuje na powierzchni stycznej w punkcie w hiperboloidy i O (1) odpowiada linii przez pochodzenie. Wiele podstawowych pojęć geometrii hiperbolicznej można opisać za pomocą liniowych terminów algebraicznych : ścieżki geodezyjne opisywane są przez przecięcia z płaszczyznami przechodzącymi przez początek układu współrzędnych, kąty dwuścienne między hiperpłaszczyznami można opisać za pomocą iloczynów wewnętrznych wektorów normalnych, a hiperboliczne grupy odbicia mogą być wyraźnie określone realizacje macierzowe.

W małych wymiarach istnieją wyjątkowe izomorfizmy grup Liego, które dają dodatkowe sposoby uwzględniania symetrii przestrzeni hiperbolicznych. Na przykład w wymiarze 2 izomorfizmy SO ⁺ (1, 2) ≅ PSL(2, R ) ≅ PSU(1, 1) pozwalają interpretować model górnej połowy płaszczyzny jako iloraz SL(2, R )/SO (2) a model dysku Poincarégo jako iloraz SU(1, 1)/U(1) . W obu przypadkach grupy symetrii działają przez ułamkowe przekształcenia liniowe, ponieważ obie grupy są stabilizatorami zachowującymi orientację w PGL(2, C ) odpowiednich podprzestrzeni sfery Riemanna. Transformacja Cayleya nie tylko przenosi jeden model płaszczyzny hiperbolicznej do drugiego, ale realizuje izomorfizm grup symetrii jako sprzężenie w większej grupie. W wymiarze 3 ułamkowe liniowe działanie PGL(2, C ) na sferę Riemanna utożsamia się z działaniem na konforemnej granicy przestrzeni hiperbolicznej 3 indukowanej izomorfizmem O ⁺ (1, 3) ≅ PGL(2, C ) . Pozwala to na badanie izometrii hiperbolicznej przestrzeni 3-przestrzennej poprzez rozważanie własności spektralnych reprezentatywnych macierzy zespolonych. Na przykład paraboliczne transformacje są sprzężone sztywnych przekładów górnej modelu półprzestrzeni i są dokładnie te przekształcenia, które mogą być reprezentowane przez unipotentne górnych trójkątnych matryce.

Zobacz też

Uwagi

Bibliografia

• A'Campo, Norbert i Papadopoulos, Athanase, (2012) Uwagi na temat geometrii hiperbolicznej , w: Strasbourg Master class on Geometry, s. 1-182, IRMA Lectures in Mathematics and Theoretical Physics, tom. 18, Zurych: Europejskie Towarzystwo Matematyczne (EMS), 461 stron, SBN ISBN  978-3-03719-105-7 , DOI 10.4171/105.
• Coxeter, HSM , (1942) Geometria nieeuklidesowa , University of Toronto Press, Toronto
• Fenchel , Werner (1989). Geometria elementarna w przestrzeni hiperbolicznej . De Gruyter Studia matematyczne. 11 . Berlin-Nowy Jork: Walter de Gruyter & Co.
• Fenchel , Werner ; Nielsen, Jakob (2003). Asmus L. Schmidt (red.). Nieciągłe grupy izometrii w płaszczyźnie hiperbolicznej . De Gruyter Studia matematyczne. 29 . Berlin: Walter de Gruyter & Co.
• Łobaczewskij, Nikołaj I., (2010) Pangeometria , pod redakcją i przekładem Athanase Papadopoulos, Dziedzictwo Matematyki Europejskiej, tom. 4. Zurych: Europejskie Towarzystwo Matematyczne (EMS). XII, 310~p, ISBN  978-3-03719-087-6 /hbk
• Milnor, John W. , (1982) Geometria hiperboliczna: Pierwsze 150 lat , Bull. Amer. Matematyka. Soc. (NS) Tom 6, Numer 1, s. 9-24.
• Reynolds, William F., (1993) Hyperbolic Geometry on a Hyperboloid , American Mathematical Monthly 100:442-455.
• Stillwell, John (1996). Źródła geometrii hiperbolicznej . Historia matematyki. 10 . Providence, RI: Amerykańskie Towarzystwo Matematyczne . Numer ISBN 978-0-8218-0529-9. MR  1402697 .
• Samuels, David, (marzec 2006) Knit Theory Discover Magazine, tom 27, numer 3.
• James W. Anderson, Geometria hiperboliczna , Springer 2005, ISBN  1-85233-934-9
• James W. Cannon, William J. Floyd, Richard Kenyon i Walter R. Parry (1997) Hyperbolic Geometry , MSRI Publications, tom 31.

Linki zewnętrzne

• Darmowy JavaScript do tworzenia szkiców w modelu dysku Poincaré na Uniwersytecie Geometrii Hiperbolicznej w Nowym Meksyku
• „The Hyperbolic Geometry Song” Krótki teledysk o podstawach geometrii hiperbolicznej dostępny na YouTube.
• „Geometria Łobaczewskiego” , Encyklopedia Matematyki , EMS Press , 2001 [1994]
• Weisstein Eric W. "Gauss-Bolyai-Lobachevsky Przestrzeń" . MatematykaŚwiat .
• Weisstein, Eric W. „Geometria hiperboliczna” . MatematykaŚwiat .
• Więcej o geometrii hiperbolicznej, w tym filmy i równania do konwersji między różnymi modelami University of Illinois at Urbana-Champaign
• Hiperboliczne diagramy Voronoi są proste, Frank Nielsen
• Stothers, Wilson (2000). „Geometria hiperboliczna” . Uniwersytet w Glasgow . Cytowanie czasopisma wymaga |journal=( pomoc ) , interaktywnej strony instruktażowej.
• Hiperboliczne mozaikowanie planarne
• Modele płaszczyzny hiperbolicznej