Twierdzenie o indeksie Atiyaha-Singera - Atiyah–Singer index theorem
| Pole | Geometria różnicowa |
|---|---|
| Pierwszy dowód autorstwa | Michael Atiyah i Isadore Singer |
| Pierwszy dowód w | 1963 |
| Konsekwencje |
Twierdzenie Cherna-Gaussa-Bonneta Twierdzenie Grothendiecka-Riemanna-Rocha Twierdzenie Hirzebrucha o sygnaturze Twierdzenie Rokhlina |
W geometrii różniczkowej The twierdzenie wskaźnik Atiyah-Singer , świadczy Michael Atiyah i Isadore Singer, (1963), stwierdza, że dla eliptycznych operator różnicowy na zwartej kolektora The Index analityczny (w odniesieniu do wymiaru przestrzeni rozwiązań) jest równa do indeksu topologicznego (zdefiniowanego na podstawie niektórych danych topologicznych). Obejmuje wiele innych twierdzeń, takich jak twierdzenie Cherna-Gaussa-Bonneta i twierdzenie Riemanna-Rocha , jako przypadki specjalne i ma zastosowanie w fizyce teoretycznej .
Historia
Problem indeksu dla eliptycznych operatorów różniczkowych postawił Israel Gel'fand . Zauważył niezmienność homotopii indeksu i poprosił o formułę za pomocą niezmienników topologicznych . Niektóre motywujących przykłady obejmowały twierdzenie Riemanna-Rocha i jego uogólnienie na twierdzenie Hirzebrucha-Riemanna-Rocha , a twierdzenie podpisu Hirzebrucha . Friedrich Hirzebruch i Armand Borel dowiedli integralności rodzaju rozmaitości spinowej, a Atiyah zasugerował, że tę integralność można wyjaśnić, gdyby była to indeks operatora Diraca (który został ponownie odkryty przez Atiyaha i Singera w 1961 roku).
Twierdzenie Atiyah-Singer zostało ogłoszone w 1963 roku. Dowód naszkicowany w tym ogłoszeniu nigdy nie został przez nich opublikowany, chociaż pojawia się w książce Palaisa. Pojawia się także w „Séminaire Cartan-Schwartz 1963/64”, które odbyło się w Paryżu równolegle z seminarium prowadzonym przez Richarda Palaisa na Uniwersytecie Princeton . Ostatnią przemowę w Paryżu wygłosił Atiyah na temat rozmaitości z granicą. Ich pierwszy opublikowany dowód zastąpił teorię kobordyzmu z pierwszego dowodu teorią K i wykorzystali ją do przedstawienia dowodów różnych uogólnień w innej sekwencji artykułów.
- 1965: Sergey P. Novikov opublikował wyniki dotyczące topologicznej niezmienności racjonalnych klas Pontriagina na gładkich rozmaitościach.
- Wyniki Robiona Kirby'ego i Laurenta C. Siebenmanna w połączeniu z artykułem René Thoma dowiodły istnienia racjonalnych klas Pontryagina na rozmaitościach topologicznych. Racjonalne klasy Pontriagina są podstawowymi składnikami twierdzenia o indeksach o rozmaitościach gładkich i topologicznych.
- 1969: Michael Atiyah definiuje abstrakcyjne operatory eliptyczne na dowolnych przestrzeniach metrycznych. Abstrakcyjne operatory eliptyczne stały się głównymi bohaterami teorii Kasparowa i nieprzemiennej geometrii różniczkowej Connesa.
- 1971: Isadore Singer proponuje kompleksowy program przyszłych rozszerzeń teorii indeksów.
- 1972: Gennadi G. Kasparov publikuje swoją pracę na temat realizacji homologii K przez abstrakcyjne operatory eliptyczne.
- 1973: Atiyah, Raoul Bott i Vijay Patodi przedstawili nowy dowód twierdzenia o indeksie za pomocą równania ciepła , opisanego w artykule Melrose'a.
- 1977: Dennis Sullivan ustanawia swoje twierdzenie o istnieniu i wyjątkowości Lipschitza i struktur quasikonformalnych na topologicznych rozmaitościach o wymiarze innym niż 4.
- 1983: Ezra Getzler, zmotywowany pomysłami Edwarda Wittena i Luisa Alvareza-Gaume'a , dał krótki dowód twierdzenia o indeksie lokalnym dla operatorów, które są lokalnymi operatorami Diraca ; obejmuje to wiele przydatnych przypadków.
- 1983: Nicolae Teleman udowadnia, że wskaźniki analityczne operatorów sygnatur z wartościami w wiązkach wektorowych są niezmiennikami topologicznymi.
- 1984: Teleman ustanawia twierdzenie o indeksie o rozmaitościach topologicznych.
- 1986: Alain Connes publikuje swój podstawowy artykuł na temat nieprzemiennej geometrii .
- 1989: Simon K. Donaldson i Sullivan badają teorię Yanga-Millsa na quasikonformalnych rozmaitościach wymiaru 4. Wprowadzają operator sygnatury S zdefiniowany na formach różniczkowych drugiego stopnia.
- 1990: Connes i Henri Moscovici udowadniają wzór na indeks lokalny w kontekście geometrii nieprzemiennej.
- 1994: Connes, Sullivan i Teleman udowadniają twierdzenie o indeksie dla operatorów sygnatur na rozmaitościach quasikonformalnych.
Notacja
- X jest zwartą gładką rozmaitością (bez granic).
- E i F są gładkimi wiązkami wektorowymi nad X .
- D jest eliptycznym operatorem różniczkowym od E do F . Tak więc we współrzędnych lokalnych działa jak operator różniczkowy, biorąc gładkie odcinki E do gładkich odcinków F .
Symbol operatora różniczkowego
Jeśli D jest różnica operatora w euklidesowej przestrzeni aby n w k zmiennych , a następnie jej symbol jest funkcją 2 k zmiennych , ponieważ przez upuszczenie wszystkie warunki, aby mniej niż n i zastąpienia przez . Zatem symbol jest jednorodny w zmiennych y stopnia n . Symbol jest dobrze zdefiniowany, mimo że nie komutuje, ponieważ zachowujemy tylko terminy najwyższego rzędu, a operatory różniczkowe komutują „do terminów niższego rzędu”. Operator nazywa się eliptycznym, jeśli symbol jest niezerowy, gdy przynajmniej jedno y jest niezerowe.
Przykład: Operator Laplace'a w k zmiennych ma symbol , a więc jest eliptyczny, ponieważ jest niezerowy, gdy którykolwiek z 's jest niezerowy. Operator falowy ma symbol , który nie jest eliptyczny if , ponieważ symbol znika dla niektórych niezerowych wartości y- ów.
Symbol operatora różnicowej aby n na gładkiej kolektora X jest zdefiniowana w ten sam sposób, za pomocą lokalnych współrzędnych wykresy, i zależy od wiązki cotangent z X , jednorodne stopnia n w każdej przestrzeni cotangent. (Ogólnie operatory różniczkowe przekształcają się w dość skomplikowany sposób pod transformacjami współrzędnych (patrz wiązka dżetów ); jednak terminy najwyższego rzędu przekształcają się jak tensory, dzięki czemu otrzymujemy dobrze zdefiniowane funkcje jednorodne na przestrzeniach kostycznych, które są niezależne od wyboru wykresów lokalnych .) Mówiąc bardziej ogólnie, symbol operatora różniczkowego między dwiema wiązkami wektorowymi E i F jest odcinkiem wycofywania wiązki Hom( E , F ) do przestrzeni kostycznej X . Operator różniczkowy nazywa się eliptycznym, jeśli element Hom( E x , F x ) jest odwracalny dla wszystkich niezerowych wektorów cotangens w dowolnym punkcie x z X .
Kluczową właściwością operatorów eliptycznych jest to, że są one prawie odwracalne; jest to ściśle związane z faktem, że ich symbole są prawie odwracalne. Dokładniej, operator eliptyczny D na zwartej rozmaitości ma (nieunikalny) parametr (lub pseudoodwrotność ) D ′ taki, że DD′ -1 i D′D -1 są operatorami zwartymi. Ważną konsekwencją jest to, że jądro D jest skończenie wymiarowe, ponieważ wszystkie przestrzenie własne operatorów zwartych, inne niż jądro, są skończenie wymiarowe. (Pseudoodwrotność eliptycznego operatora różniczkowego prawie nigdy nie jest operatorem różniczkowym, ale jest to eliptyczny operator pseudoróżniczkowy .)
Indeks analityczny
Ponieważ eliptyczny operator różniczkowy D ma pseudoodwrotność, jest to operator Fredholma . Każdy operator Fredholm ma wskaźnik , określa się jako różnicę pomiędzy (Finite) wymiar jądra z D (roztwory Df = 0), i (Finite) wymiar cokernel z D (ograniczeń w prawym ręcznego strony niejednorodnego równania, takiego jak Df = g , lub równoważnie jądra operatora sprzężonego). Innymi słowy,
- Indeks( D ) = dim Ker(D) − dim Coker( D ) = dim Ker(D) − dim Ker( D* ).
To czasem nazywa się wskaźnikiem analitycznej z D .
Przykład: Załóżmy, że rozmaitością jest okrąg (myślimy, że R / Z ), a D jest operatorem d/dx − λ dla pewnej zespolonej stałej λ. (Jest to najprostszy przykład operatora eliptycznego.) Wtedy jądro jest przestrzenią wielokrotności exp(λ x ) jeśli λ jest całkowitą wielokrotnością 2π i, a w przeciwnym razie wynosi 0, a jądro sprzężenia jest podobną przestrzenią z λ zastąpionym jego sprzężeniem złożonym. Tak więc D ma indeks 0. Ten przykład pokazuje, że jądro i kokernel operatorów eliptycznych mogą przeskakiwać w sposób nieciągły, gdy zmienia się operator eliptyczny, więc nie ma ładnego wzoru na ich wymiary w kategoriach ciągłych danych topologicznych. Jednak skoki wymiarów jądra i koksu są takie same, więc indeks, określony przez różnicę ich wymiarów, rzeczywiście zmienia się w sposób ciągły i może być podany w kategoriach danych topologicznych przez twierdzenie o indeksie.
Indeks topologiczny
Wskaźnik topologiczna eliptycznej operator różnicowy pomiędzy gładkimi wiązek wektora i na o wymiarowej zwartej kolektora jest przez
innymi słowy, wartość składnika górnowymiarowego mieszanej klasy kohomologii w podstawowej klasie homologii rozmaitości . Tutaj,
- jest klasą Todd złożonej wiązki stycznej .
-
jest równe , gdzie
- jest izomorfizmem Thoma dla wiązki sfer
- to postać Cherna
- jest „elementem różnicy” związanym z dwoma wiązkami wektorowymi i dalej oraz izomorfizmem między nimi w podprzestrzeni .
- jest symbolem
Można również zdefiniować indeks topologiczny używając tylko K-teorii (i ta alternatywna definicja jest w pewnym sensie zgodna z powyższą konstrukcją znaku Cherna). Jeśli X jest zwartą podrozmaitością rozmaitości Y, to istnieje odwzorowanie w przód (lub „wrzask”) od K( TX ) do K( TY ). Indeks topologiczny elementu K( TX ) jest zdefiniowany jako obraz tej operacji z Y pewną przestrzenią euklidesową, dla której K( TY ) można w naturalny sposób utożsamić z liczbami całkowitymi Z (jako konsekwencja okresowości Botta). Ta mapa jest niezależna od osadzenia X w przestrzeni euklidesowej. Teraz operator różniczkowy, jak wyżej, naturalnie definiuje element K( TX ), a obraz w Z pod tą mapą „jest” indeksem topologicznym.
Jak zwykle, D jest eliptycznym operatorem różniczkowym między wiązkami wektorowymi E i F nad zwartą rozmaitością X .
Problemem wskaźnik jest następujący: obliczyć (analityczny) indeks D , przy wykorzystaniu jedynie symbolem a i topologiczne danych pochodzących z kolektora i wiązki wektora. Twierdzenie o indeksie Atiyaha-Singera rozwiązuje ten problem i stwierdza:
- Indeks analityczny D jest równy jego indeksowi topologicznemu.
Pomimo swojej budzącej grozę definicji indeks topologiczny jest zwykle łatwy do jednoznacznej oceny. Dzięki temu możliwa jest ocena wskaźnika analitycznego. (Kokernel i jądro operatora eliptycznego są na ogół niezwykle trudne do indywidualnej oceny; twierdzenie o indeksie pokazuje, że zwykle możemy przynajmniej oszacować ich różnicę .) Wiele ważnych niezmienników rozmaitości (takich jak sygnatura) można podać jako indeks odpowiednich operatorów różniczkowych, więc twierdzenie o indeksie pozwala nam ocenić te niezmienniki pod względem danych topologicznych.
Chociaż wskaźnik analityczny jest zwykle trudny do bezpośredniej oceny, przynajmniej w oczywisty sposób jest liczbą całkowitą. Indeks topologiczny jest z definicji liczbą wymierną, ale zwykle z definicji wcale nie wynika, że jest on również całkowy. Tak więc twierdzenie o indeksie Atiyaha-Singera implikuje pewne głębokie własności integralności, ponieważ implikuje, że indeks topologiczny jest całkowy.
Indeks eliptycznego operatora różniczkowego oczywiście znika, jeśli operator jest samosprzężony. Znika również, jeśli rozmaitość X ma nieparzysty wymiar, chociaż istnieją pseudoróżniczkowe operatory eliptyczne, których indeks nie znika w nieparzystych wymiarach.
Stosunek do Grothendiecka–Riemann–Roch
Twierdzenie Grothendiecka–Riemanna–Rocha było jedną z głównych motywacji twierdzenia o indeksie, ponieważ twierdzenie o indeksie jest odpowiednikiem tego twierdzenia w układzie rzeczywistych rozmaitości. Teraz, jeśli istnieje mapa zwartych, stabilnych, prawie złożonych rozmaitości, to istnieje diagram przemienny
jeśli jest to punkt, to odzyskujemy powyższe stwierdzenie. Tutaj jest grupa Grothendiecka złożonych wiązek wektorowych. Ten diagram przemienny jest formalnie bardzo podobny do twierdzenia GRR, ponieważ grupy kohomologii po prawej stronie są zastąpione pierścieniem Chow odmiany gładkiej, a grupa Grothendiecka po lewej jest podana przez grupę Grothendiecka algebraicznych wiązek wektorowych.
Rozszerzenia twierdzenia o indeksie Atiyah-Singera
Twierdzenie o indeksie Telemana
Ze względu na ( Teleman 1983 ), ( Teleman 1984 ):
- Dla dowolnego abstrakcyjnego operatora eliptycznego ( Atiyah 1970 ) na zamkniętej, zorientowanej rozmaitości topologicznej, indeks analityczny jest równy indeksowi topologicznemu.
Dowód tego wyniku przechodzi przez konkretne rozważania, w tym rozszerzenie teorii Hodge'a na rozmaitości kombinatoryczne i Lipschitza ( Teleman 1980 ), ( Teleman 1983 ), rozszerzenie operatora podpisu Atiyaha-Singera na rozmaitości Lipschitza ( Teleman 1983 ), K-Kasparowa homologia ( Kasparow 1972 ) i topologiczny kobordyzm ( Kirby i Siebenmann 1977 ).
Wynik ten pokazuje, że twierdzenie o indeksie nie jest jedynie twierdzeniem o różniczkowalności, ale raczej twierdzeniem topologicznym.
Twierdzenie o indeksie Connesa–Donaldsona–Sullivana–Telemana
Ze względu na ( Donaldson & Sullivan 1989 ), ( Connes, Sullivan & Teleman 1994 ):
- Dla każdej quasikonformalnej rozmaitości istnieje lokalna konstrukcja klas charakterystycznych Hirzebrucha–Thoma.
Teoria ta opiera się na operatorze sygnatury S , zdefiniowanym na formach różniczkowych średniego stopnia na parzystowymiarowych rozmaitościach quasikonformalnych (porównaj ( Donaldson i Sullivan 1989 )).
Korzystając z topologicznego kobordyzmu i K-homologii, można w pełni przedstawić twierdzenie indeksowe o rozmaitościach quasikonformalnych (patrz strona 678 ( Connes, Sullivan & Teleman 1994 )). Praca ( Connes, Sullivan i Teleman 1994 ) „zapewnia lokalne konstrukcje dla klas charakterystycznych w oparciu o wyżej wymiarowe pokrewne mierzalnego odwzorowania Riemanna w wymiarze drugim i teorii Yanga-Millsa w wymiarze czwartym”.
Wyniki te stanowią znaczący postęp na wzór programu Singera Perspektywy w matematyce ( Singer 1971 ). Jednocześnie zapewniają one również efektywną konstrukcję racjonalnych klas Pontrjagin na rozmaitościach topologicznych. Artykuł ( Teleman 1985 ) dostarcza powiązania między oryginalną konstrukcją Thoma racjonalnych klas Pontrjagin ( Thom 1956 ) a teorią indeksów.
Należy wspomnieć, że formuła indeksu jest stwierdzeniem topologicznym. Teorie przeszkód stworzone przez Milnora, Kervaire'a, Kirby'ego, Siebenmanna, Sullivana, Donaldsona pokazują, że tylko nieliczne rozmaitości topologiczne posiadają struktury różniczkowalne i niekoniecznie są one unikalne. Wynik Sullivana dotyczący Lipschitza i struktur quasikonformalnych ( Sullivan 1979 ) pokazuje, że każda rozmaitość topologiczna w wymiarze innym niż 4 posiada taką strukturę, która jest unikalna (aż do izotopii bliskiej identyczności).
Struktury quasikonformalne ( Connes, Sullivan i Teleman 1994 ) i bardziej ogólnie struktury L p , p > n(n+1)/2 , wprowadzone przez M. Hilsum ( Hilsum 1999 ), są najsłabszymi strukturami analitycznymi na topologicznych rozmaitościach wymiar n, dla którego znane jest twierdzenie o indeksie.
Inne rozszerzenia
- Twierdzenie Atiyaha-Singera stosuje się do eliptycznych operatorów pseudoróżniczkowych w taki sam sposób, jak do eliptycznych operatorów różniczkowych. W rzeczywistości, z przyczyn technicznych większość wczesnych dowodów działała z operatorami pseudodyferencjalnymi, a nie różniczkowymi: ich dodatkowa elastyczność sprawiała, że niektóre etapy dowodu były łatwiejsze.
- Zamiast pracować z operatorem eliptycznym między dwiema wiązkami wektorowymi, czasami wygodniej jest pracować z kompleksem eliptycznym
- wiązek wektorowych. Różnica polega na tym, że symbole tworzą teraz dokładną sekwencję (poza sekcją zerową). W przypadku, gdy w kompleksie są tylko dwie niezerowe wiązki, oznacza to, że symbol jest izomorfizmem poza sekcją zerową, więc zespół eliptyczny z 2 członami jest zasadniczo taki sam jak operator eliptyczny między dwoma wiązkami wektorowymi. I odwrotnie, twierdzenie o indeksie dla kompleksu eliptycznego można łatwo sprowadzić do przypadku operatora eliptycznego: dwie wiązki wektorowe są podane przez sumy parzystych lub nieparzystych członów kompleksu, a operator eliptyczny jest sumą operatorów kompleks eliptyczny i jego sprzężenia, ograniczone do sumy parzystych wiązek.
- Jeśli rozmaitość może mieć brzeg, to należy nałożyć pewne ograniczenia na dziedzinę operatora eliptycznego, aby zapewnić indeks skończony. Warunki te mogą być lokalne (na przykład wymaganie, aby sekcje w domenie znikały na granicy) lub bardziej skomplikowane warunki globalne (na przykład wymaganie, aby sekcje w domenie rozwiązały jakieś równanie różniczkowe). Przypadek lokalny opracowali Atiyah i Bott, ale wykazali, że wiele interesujących operatorów (np. operator sygnatury ) nie dopuszcza lokalnych warunków brzegowych. Aby poradzić sobie z tymi operatorami, Atiyah , Patodi i Singer wprowadzili globalne warunki brzegowe równoważne przyłączeniu cylindra do kolektora wzdłuż granicy, a następnie ograniczeniu dziedziny do tych odcinków, które można całkować do kwadratu wzdłuż cylindra. Ten punkt widzenia jest przyjęte w dowodzie Melrose (1993) z twierdzenia indeksu Atiyah-Patodi-Singer .
- Zamiast jednego operatora eliptycznego można rozważyć rodzinę operatorów eliptycznych sparametryzowaną przez pewną przestrzeń Y . W tym przypadku indeks jest elementem K-teorii Y , a nie liczbą całkowitą. Jeśli operatory w rodzinie są rzeczywiste, to indeks leży w rzeczywistej K-teorii Y . Daje to trochę dodatkowych informacji, ponieważ mapa od rzeczywistej K-teorii Y do złożonej K-teorii nie zawsze jest iniektywna.
- Jeśli istnieje działanie grupowe grupy G na zwartej rozmaitości X , komutującej z operatorem eliptycznym, to zwykłą K-teorię zastępuje się K-teorią ekwiwariantną . Ponadto uzyskuje się uogólnienia twierdzenia Lefschetza o punkcie stałym , z terminami pochodzącymi z podrozmaitości punktu stałego grupy G . Zobacz też: twierdzenie o indeksie ekwiwariantnym .
- Atiyah (1976) pokazał, jak rozszerzyć twierdzenie o indeksie na pewne niezwarte rozmaitości, na które oddziałuje grupa dyskretna o zwartym ilorazie. Jądro operatora eliptycznego jest w tym przypadku ogólnie nieskończenie wymiarowe, ale możliwe jest uzyskanie skończonego indeksu przy użyciu wymiaru modułu nad algebrą von Neumanna ; indeks ten jest na ogół wartością rzeczywistą, a nie całkowitą. Ta wersja jest nazywany L 2 twierdzenie indeks i był stosowany przez Atiyah i Schmid (1977) do rederive właściwości dyskretnych reprezentacji serii z półprosty grup Lie .
- Twierdzenie Indeks Kallias jest twierdzenie wskaźnik dla operatora Diraca na niezagęszczonymi przestrzeni jednowymiarowej dziwne. Indeks Atiyah-Singer jest zdefiniowany tylko na zwartych przestrzeniach i znika, gdy ich wymiar jest nieparzysty. W 1978 roku Constantine Callias , na sugestię swojego doktora. doradca Roman Jackiw wykorzystał anomalię osiową do wyprowadzenia tego twierdzenia o indeksie na przestrzeniach wyposażonych w macierz hermitowską zwaną polem Higgsa . Indeks operatora Diraca jest topologicznym niezmiennikiem, który mierzy uzwojenie pola Higgsa na kuli w nieskończoności. Jeśli U jest macierzą jednostkową w kierunku pola Higgsa, to indeks jest proporcjonalny do całki U ( dU ) n -1 po sferze ( n -1) w nieskończoności. Jeśli n jest parzyste, to zawsze jest równe zero.
- Topologiczna interpretacja tego niezmiennika i jego związek ze wskaźnikiem Hörmandera zaproponowana przez Borisa Fedosova , uogólniona przez Larsa Hörmandera , została opublikowana przez Raoula Botta i Roberta Thomasa Seeleya .
Przykłady
Charakterystyka Eulera
Załóżmy, że M jest rozmaitością zorientowaną zwartą. Jeśli przyjmiemy, że E jest sumą parzystych potęg zewnętrznych wiązki cotangensa, a F jest sumą potęg nieparzystych, zdefiniuj D = d + d* , rozpatrywane jako odwzorowanie od E do F . Następnie wskaźnik topologicznych D jest charakterystyczny Eulera na kohomologiami Hodge o M a wskaźnik analitycznym jest klasa Eulera kolektora. Formuła indeksu dla tego operatora daje twierdzenie Cherna–Gaussa–Bonneta .
Twierdzenie Hirzebrucha–Riemanna–Rocha
Weź X jako złożoną rozmaitość z holomorficzną wiązką wektorów V . Niech wiązki wektorowe E i F będą sumami wiązek form różniczkowych o współczynnikach V typu (0, i ) z i parzystym lub nieparzystym, a operator różniczkowy D będzie sumą
ograniczone do E . Następnie wskaźnik analityczne D jest holomorficzny Eulera charakterystyczne z V :
Indeks topologiczny D jest podany przez
- ,
iloczyn charakteru Cherna V i klasy Todda X oceniany na podstawowej klasie X . Zrównując indeksy topologiczne i analityczne otrzymujemy twierdzenie Hirzebrucha–Riemanna–Rocha . W rzeczywistości otrzymujemy uogólnienie tego na wszystkie złożone rozmaitości: dowód Hirzebrucha działał tylko dla rzutowych rozmaitości zespolonych X .
To wyprowadzenie twierdzenia Hirzebrucha-Riemanna-Rocha jest bardziej naturalne, jeśli użyjemy twierdzenia o indeksie dla kompleksów eliptycznych, a nie operatorów eliptycznych. Możemy przyjąć, że kompleks jest
z różnicą podaną przez . Następnie i” th grupa kohomologie jest tak spójna grupa kohomologie H I ( X , V ), a więc współczynnik analityczne kompleks jest holomorficzny Eulera charakterystyczne Σ (-1) i słabe (H I ( X , V )). Tak jak poprzednio, indeks topologiczny to ch( V )Td( X )[ X ].
Twierdzenie Hirzebrucha o sygnaturze
Twierdzenie Hirzebrucha o sygnaturze mówi, że sygnatura zwartej zorientowanej rozmaitości X o wymiarze 4 k jest dana przez rodzaj L rozmaitości. Wynika to z twierdzenia o indeksie Atiyaha-Singera zastosowanego do następującego operatora podpisu .
Wiązki E i F są dane przez przestrzenie własne +1 i -1 operatora na wiązce form różniczkowych X , który działa na k -formach jako
razy operator Hodge * . Operatorem D jest Hodge Laplacian
ograniczone do E , gdzie d jest zewnętrzną pochodną Cartana , a d * jest jej sprzężeniem.
Indeks analityczny D jest sygnaturą rozmaitości X , a jej indeks topologiczny to rodzaj L X , więc są one równe.
 rodzaj i twierdzenie Rochlina
Rodzaj A jest liczbą wymierną zdefiniowane dla każdego kolektora, ale na ogół nie jest całkowita. Borel i Hirzebruch wykazali, że jest to całka dla rozmaitości spinowych, a parzysta liczba całkowita, jeśli dodatkowo wymiar wynosi 4 mod 8. Można to wywnioskować z twierdzenia o indeksie, z którego wynika, że rodzaj rozmaitości spinowych jest indeksem Diraca. operator. Dodatkowy czynnik 2 w wymiarach 4 mod 8 wynika z faktu, że w tym przypadku jądro i koker operatora Diraca mają strukturę czwartorzędową, więc jako złożone przestrzenie wektorowe mają parzyste wymiary, więc indeks jest parzysty.
W wymiarze 4 wynik ten implikuje twierdzenie Rochlina, że sygnatura czterowymiarowej rozmaitości spinowej jest podzielna przez 16: wynika to z tego, że w wymiarze 4 rodzaj  jest minus jedna ósma sygnatury.
Techniki dowodowe
Operatory pseudoróżnicowe
Operatory pseudodyferencjalne można łatwo wyjaśnić w przypadku operatorów o stałym współczynniku w przestrzeni euklidesowej. W tym przypadku operatory różniczkowe o stałym współczynniku są po prostu transformatami Fouriera mnożenia przez wielomiany, a operatory pseudoróżnicowe o stałym współczynniku są po prostu transformatami Fouriera mnożenia przez bardziej ogólne funkcje.
Wiele dowodów twierdzenia o indeksie używa operatorów pseudoróżnicowych zamiast operatorów różniczkowych. Powodem tego jest to, że dla wielu celów nie ma wystarczającej liczby operatorów różniczkowych. Na przykład pseudoodwrotność eliptycznego operatora różniczkowego dodatniego rzędu nie jest operatorem różniczkowym, ale jest operatorem pseudoróżniczkowym. Istnieje również bezpośrednia zgodność między danymi reprezentującymi elementy K(B( X ), S ( X )) (funkcje sprzężenia) a symbolami eliptycznych operatorów pseudoróżnicowych.
Operatory pseudoróżniczkowe mają porządek, który może być dowolną liczbą rzeczywistą lub nawet −∞, i mają symbole (które nie są już wielomianami w przestrzeni kostycznej), a eliptyczne operatory różniczkowe to te, których symbole są odwracalne dla wystarczająco dużych wektorów kostycznych. Większość wersji twierdzenia o indeksie można rozszerzyć z eliptycznych operatorów różniczkowych na eliptyczne operatory pseudoróżnicowe.
Kobordyzm
Pierwotny dowód opierał się na twierdzeniu Hirzebrucha-Riemanna-Rocha (1954) i obejmował teorię kobordyzmu i operatory pseudoróżnicowe .
Idea tego pierwszego dowodu jest z grubsza następująca. Rozważmy pierścień generowany przez pary ( X , V ) gdzie V jest gładką wiązką wektorów na zwartej gładko zorientowanej rozmaitości X , z zależnościami, w których suma i iloczyn pierścienia na tych generatorach są dane przez sumę rozłączną i iloczyn rozmaitości (z oczywiste operacje na wiązkach wektorowych), a dowolna granica rozmaitości z wiązką wektorów wynosi 0. Jest to podobne do pierścienia kobordyzmu rozmaitości zorientowanych, z tym wyjątkiem, że rozmaitości mają również wiązkę wektorów. Wskaźniki topologiczne i analityczne są reinterpretowane jako funkcje od tego pierścienia do liczb całkowitych. Następnie sprawdzamy, czy te dwie funkcje są w rzeczywistości homomorfizmami pierścieniowymi. Aby udowodnić, że są takie same, wystarczy sprawdzić, czy są takie same na zestawie generatorów tego pierścienia. Teoria kobordyzmu Thoma podaje zestaw generatorów; na przykład złożone przestrzenie wektorowe z wiązką trywialną wraz z pewnymi wiązkami nad sferami parzystymi. Tak więc twierdzenie o indeksie można udowodnić, sprawdzając je w tych szczególnie prostych przypadkach.
K-teoria
Pierwszy opublikowany dowód Atiyaha i Singera wykorzystywał teorię K, a nie kobordyzm. Jeśli i jest dowolnym włączeniem zwartych rozmaitości od X do Y , zdefiniowali oni operację 'pushforward' i ! na operatorach eliptycznych X na operatory eliptyczne Y, które zachowują indeks. Biorąc Y za jakąś sferę, w której osadzony jest X , redukuje to twierdzenie o indeksie do przypadku sfer. Jeśli Y jest sferą, a X jest punktem osadzonym w Y , to każdy operator eliptyczny na Y jest obrazem pod i ! jakiegoś operatora eliptycznego na punkcie. Sprowadza to twierdzenie o indeksie do przypadku punktu, w którym jest ono trywialne.
Równanie ciepła
Atiyah, Bott i Patodi ( 1973 ) przedstawili nowy dowód twierdzenia o indeksie za pomocą równania ciepła , patrz np. Berline, Getzler i Vergne (1992) . Dowód jest również opublikowany w ( Melrose 1993 ) i ( Gilkey 1994 ).
Jeśli D jest operatorem różniczkowym ze sprzężonym D* , to D*D i DD* są operatorami samosprzężonymi, których niezerowe wartości własne mają te same krotności. Jednak ich zerowe przestrzenie własne mogą mieć różne krotności, ponieważ te krotności są wymiarami jąder D i D* . Dlatego indeks D jest podany przez
dla dowolnego dodatniego t . Po prawej stronie znajduje się ślad różnicy ziaren dwóch operatorów cieplnych. Mają one asymptotyczną ekspansję dla małych dodatnich t , które można wykorzystać do oceny granicy, gdy t dąży do 0, dając dowód twierdzenia o indeksie Atiyaha-Singera. Rozwinięcia asymptotyczne dla małego t wydają się bardzo skomplikowane, ale teoria niezmiennicza pokazuje, że między wyrazami występują ogromne anulowania, co umożliwia jednoznaczne znalezienie wyrazów wiodących. Te odwołania zostały później wyjaśnione za pomocą supersymetrii.
Cytaty
Bibliografia
Artykuły Atiyah są przedrukowane w tomach 3 i 4 jego prac zebranych (Atiyah 1988a , 1988b )
- Atiyah, MF (1970), "Globalna teoria operatorów eliptycznych", Proc. wewn. Konf. Analiza funkcjonalna i tematy pokrewne (Tokio, 1969) , Uniwersytet w Tokio, Zbl 0193.43601
- Atiyah, MF (1976), „Operatory eliptyczne, grupy dyskretne i algebry von Neumanna”, Colloque „Analyse et Topologie” en l'Honneur de Henri Cartan (Orsay, 1974) , Asterisque, 32-33, Soc. Matematyka. Francja, Paryż, s. 43–72, MR 0420729
- Atiyah, MF ; Segal, GB (1968), "Indeks operatorów eliptycznych: II", Annals of Mathematics , Druga seria, 87 (3): 531-545, doi : 10.2307/1970716 , JSTOR 1970716 To przeformułowuje wynik jako rodzaj twierdzenia Lefschetza o punkcie stałym, używając ekwiwariantnej K-teorii.
- Atiyah, Michael F .; Singer, Isadore M. (1963), "Indeks operatorów eliptycznych na kompaktowych rozgałęźnikach", Bull. Amer. Matematyka. Soc. , 69 (3): 422–433, doi : 10.1090/S0002-9904-1963-10957-X Zapowiedź twierdzenia o indeksie.
- Atiyah, Michael F .; Singer, Isadore M. (1968a), "Indeks operatorów eliptycznych I", Annals of Mathematics , 87 (3): 484-530, doi : 10.2307/1970715 , JSTOR 1970715 Daje to dowód za pomocą teorii K zamiast kohomologii.
- Atiyah, Michael F .; Singer, Isadore M. (1968b), "Indeks operatorów eliptycznych III", Annals of Mathematics , Druga seria, 87 (3): 546-604, doi : 10.2307/1970717 , JSTOR 190717 Ten artykuł pokazuje, jak dokonać konwersji z wersji K-teorii do wersji przy użyciu kohomologii.
- Atiyah, Michael F .; Singer, Isadore M. (1971a), "Indeks operatorów eliptycznych IV", Annals of Mathematics , Druga seria, 93 (1): 119-138, doi : 10.2307/1970756 , JSTOR 1970756 W artykule tym badane są rodziny operatorów eliptycznych, gdzie indeks jest obecnie elementem K-teorii przestrzeni parametryzującej rodzinę.
- Atiyah, Michael F .; Singer, Isadore M. (1971b), "Indeks operatorów eliptycznych V", Annals of Mathematics , Druga seria, 93 (1): 139-149, doi : 10.2307/1970757 , JSTOR 1970757. Badanie to bada rodziny rzeczywistych (a nie złożonych) operatorów eliptycznych, podczas gdy czasami można wycisnąć trochę dodatkowych informacji.
- Atiyah, MF ; Bott, R. (1966), "Formuła punktu stałego Lefschetza dla eliptycznych operatorów różniczkowych", Bull. Jestem. Matematyka. Soc. , 72 (2): 245-50, doi : 10,1090 / S0002-9904-1966-11483-0. Stanowi to twierdzenie obliczające liczbę Lefschetza endomorfizmu kompleksu eliptycznego.
- Atiyah, MF ; Bott, R. (1967), "A Lefschetz Formuła Punktu Stałego dla kompleksów eliptycznych: I", Annals of Mathematics , Druga seria, 86 (2): 374-407, doi : 10.2307/1970694 , JSTOR 1970694i Atiyah, MF; Bott, R. (1968), "A Lefschetz Formuła Punktu Stałego dla kompleksów eliptycznych: II. Zastosowania", Annals of Mathematics , Druga seria, 88 (3): 451-491, doi : 10.2307/1970721 , JSTOR 1970721 Dają one dowody i niektóre zastosowania wyników ogłoszonych w poprzednim artykule.
- Atiyah, M .; Bott, R .; Patodi, VK (1973), „O równaniu ciepła i twierdzeniu o indeksie”, Invent. Matematyka. , 19 (4): 279–330, Bibcode : 1973InMat..19..279A , doi : 10.1007/BF01425417 , MR 0650828 , S2CID 115700319. Atiyah, M.; Bott, R.; Patodi, VK (1975), „Errata”, Wymyśl. Matematyka. , 28 (3): 277–280, Bibcode : 1975InMat..28..277A , doi : 10.1007/BF01425562 , MR 0650829
- Atiyah, Michael ; Schmid, Wilfried (1977), „geometryczna konstrukcja szeregu dyskretnego dla półprostych grup Liego”, Invent. Matematyka. , 42 : 1-62, Bibcode : 1977InMat..42....1A , doi : 10.1007/BF01389783 , MR 0463358 , S2CID 189831012, Atiyah, Michael; Schmid, Wilfried (1979), „Erratum”, Wymyśl. Matematyka. , 54 (2): 189–192, Bibcode : 1979InMat..54..189A , doi : 10.1007/BF01408936 , MR 0550183
- Atiyah, Michael (1988a), Dzieła zebrane. Tom. 3. Teoria indeksów: 1 , Oxford Science Publications, Nowy Jork: The Clarendon Press, Oxford University Press, ISBN 978-0-19-853277-4, numer MR 0951894
- Atiyah, Michael (1988b), Dzieła zebrane. Tom. 4. Teoria indeksów: 2 , Oxford Science Publications, Nowy Jork: The Clarendon Press, Oxford University Press, ISBN 978-0-19-853278-1, numer MR 0951895
- Baum, P .; Fulton, W .; Macpherson, R. (1979), "Riemann-Roch dla pojedynczych odmian" , Acta Mathematica , 143 : 155-191, doi : 10.1007/BF02684299 , S2CID 83458307 , Zbl 0332.14003
- Berlinie, Nicole; Getzler, Ezdrasz; Vergne, Michele (1992), Heat Kernels i Dirac Operators , Berlin: Springer, ISBN 978-3-540-53340-5 Daje to elementarny dowód twierdzenia o indeksie dla operatora Diraca, używając równania ciepła i supersymetrii.
- Bismut, Jean-Michel (1984), „Twierdzenia Atiyah-Singer: podejście probabilistyczne. I. Twierdzenie o indeksie”, J. Funct. Analiza , 57 : 56–99, doi : 10.1016/0022-1236(84)90101-0 Bismut udowadnia twierdzenie o kompleksach eliptycznych przy użyciu metod probabilistycznych, a nie metod równań cieplnych.
- Cartan-Schwartz (1965), Seminarium Henri Cartan. Théoreme d'Atiyah-Singer sur l'indice d'un opérateur différentiel elliptique. 16 lat: 1963/64 dirigee Henri Cartana i Laurenta Schwartza. Fas. 1; Fas. 2. (Francuski) , École Normale Supérieure, Secrétariat mathématique, Paryż, Zbl 0149.41102
- Connes, A. (1986), „Nieprzemienna geometria różniczkowa” , Publikacje Mathématiques de l'Institut des Hautes Études Scientifiques , 62 : 257-360, doi : 10.1007/BF02698807 , S2CID 122740195 , Zbl 0592.46056
- Connes, A. (1994), Geometria nieprzemienna , San Diego: Academic Press, ISBN 978-0-12-185860-5, Zbl 0818.46076
- Connes, A .; Moscovici, H. (1990), "Cykliczna kohomologia, przypuszczenie Novikova i grupy hiperboliczne" (PDF) , Topologia , 29 (3): 345-388, doi : 10.1016/0040-9383(90)90003-3 , Zbl 0759.58047
- Connes, A .; Sullivan, D .; Teleman, N. (1994), "Quasiconformal mappings, operators on Hilbert space and local formulas for specific class", Topology , 33 (4): 663-681, doi : 10.1016/0040-9383(94)90003-5 , Zbl 0840.57013
- Donaldson, SK ; Sullivan, D. (1989), "Quasiconformal 4-rozmaitości", Acta Mathematica , 163 : 181-252, doi : 10.1007/BF02392736 , Zbl 0704.57008
- Gel'fand, IM (1960), „Na równaniach eliptycznych”, Russ. Matematyka. Surv. , 15 (3): 113–123, Bibcode : 1960RuMaS..15..113G , doi : 10.1070/rm1960v015n03ABEH004094przedrukowane w tomie I jego dzieł zebranych, s. 65-75, ISBN 0-387-13619-3 . Na stronie 120 Gel'fand sugeruje, że indeks operatora eliptycznego powinien być wyrażalny w kategoriach danych topologicznych.
- Getzler, E. (1983), „Pseudróżnicowe operatory na superrozmaitościach i twierdzenie o indeksie Atiyaha-Singera” , Commun. Matematyka. Fiz. , 92 (2): 163–178, Bibcode : 1983CMaPh..92..163G , doi : 10.1007/BF01210843 , S2CID 55438589
- Getzler, E. (1988), "Krótki dowód lokalnego twierdzenia o indeksie Atiyah-Singera", Topologia , 25 : 111-117, doi : 10.1016/0040-9383 (86) 90008-X
- Gilkey, Peter B. (1994), teoria niezmienności , równanie ciepła i twierdzenie Atiyaha-Singera , ISBN 978-0-8493-7874-4 Bezpłatny podręcznik online, który udowadnia twierdzenie Atiyaha-Singera z podejściem równania ciepła
- Hamilton, MJD (2020). „Bozon Higgsa dla matematyków. Notatki z wykładów na temat teorii cechowania i łamania symetrii”. arXiv : 1512.02632 [ math.DG ].
- Kayani, U. (2020). „Dynamiczne wzmocnienie supersymetrii horyzontów czarnych dziur”. arXiv : 1910.01080 [ hep-th ].
- Higson, Nigel; Roe, John (2000), Analityczna K-homologia , Oxford University Press, ISBN 9780191589201
- Hilsum, M. (1999), "struktury riemaniennes L P i K -homologie", Annals of matematyki , 149 (3): 1007/22, arXiv : Math / 9905210 , doi : 10,2307 / 121079 , JSTOR 121079 , S2CID 119708566
- Kasparow, GG (1972), „Niezmienność topologiczna operatorów eliptycznych, I: Homologia K”, Matematyka. USSR Izvestija (tł. ang.) , 9 (4): 751–792, Bibcode : 1975IzMat...9..751K , doi : 10.1070/IM1975v009n04ABEH001497
- Kirby, R .; Siebenmann, LC (1969), „O triangulacji rozmaitości i Hauptvermutung”, Bull. Amer. Matematyka. Soc. , 75 (4): 742–749, doi : 10.1090/S0002-9904-1969-12271-8
- Kirby, R .; Siebenmann, LC (1977), podstawowe eseje o topologicznych rozmaitościach, wygładzaniach i triangulacjach , Annals of Mathematics Studies in Mathematics, 88 , Princeton: Princeton University Press i Tokio University Press
- Melrose, Richard B. (1993), twierdzenie o indeksie Atiyah-Patodi-Singer , Wellesley, Massachusetts: Peters, ISBN 978-1-56881-002-7 Bezpłatny podręcznik online.
- Novikov SP (1965), „Topologiczna niezmienność racjonalnych klas Pontrjagin” (PDF) , Doklady Akademii Nauk SSSR , 163 : 298–300
- Palais, Richard S. (1965), Seminarium na temat twierdzenia o indeksie Atiyah-Singera , Annals of Mathematics Studies, 57 , SL: Princeton Univ Press, ISBN 978-0-691-08031-4 To opisuje oryginalny dowód twierdzenia (Atiyah i Singer nigdy sami nie opublikowali swojego oryginalnego dowodu, a jedynie jego ulepszone wersje).
- Shanahan, P. (1978), twierdzenie o indeksie Atiyah-Singera: wprowadzenie , Uwagi do wykładu z matematyki, 638 , Springer, CiteSeerX 10.1.1.193.9222 , doi : 10.1007/BFb0068264 , ISBN 978-0-387-08660-6
- Singer, IM (1971), „Przyszłe rozszerzenia teorii indeksów i operatorów eliptycznych”, Prospects in Mathematics , Annals of Mathematics Studies in Mathematics , 70 , s. 171-185
- Sullivan, D. (1979), „Hiperboliczna geometria i homeomorfizmy”, JC Candrell, „Topologia geometryczna”, Proc. Konf. topologii Gruzji Ateny, Georgia, 1977 , Nowy Jork: Academic Press, s. 543-595, ISBN 978-0-12-158860-1, Zbl 0478.57007
- Sullivan, D .; Teleman, N. (1983), "An analityczny dowód twierdzenia Novikov dotyczącego racjonalnych klas Pontrjagin" , Publikacje mathématiques de l'Institut des Hautes Études Scientifiques , Paryż, 58 : 291-293, doi : 10.1007 / BF02953773 , S2CID 8348213 , Zbl 0531.58045
- Teleman, N. (1980), "Combinatorial Hodge teoria i operator sygnatur", Inventiones Mathematicae , 61 (3): 227-249, Bibcode : 1980InMat..61..227T , doi : 10.1007/BF01390066 , S2CID 122247909
- Teleman, N. (1983), „Indeks operatorów podpisów na rozmaitościach Lipschitza” , Publications Mathématiques de l'Institut des Hautes Études Scientifiques , 58 : 251-290, doi : 10.1007/BF02953772 , S2CID 121497293 , Zbl 0531.58044
- Teleman, N. (1984), „Twierdzenie o indeksie o rozmaitościach topologicznych”, Acta Mathematica , 153 : 117-152, doi : 10.1007/BF02392376 , Zbl 0547.58036
- Teleman, N. (1985), "Przekroczenie i twierdzenie o indeksie", równania całkowe i teoria operatorów , 8 (5): 693-719, doi : 10.1007/BF01201710 , S2CID 121137053
- Thom, R. (1956), „Les classs caractéristiques de Pontrjagin de variétés triangulées”, Symp. wewn. Szczyt. Alg. Meksyk , s. 54–67
- Witten, Edward (1982), "Supersymetria i teoria Morse'a", J. Diff. Geom. , 17 (4): 661–692, doi : 10.4310/jdg/1214437492 , MR 0683171
- Shing-Tung Yau , wyd. (2009) [Pierwsze wydanie w 2005], The Founders of Index Theory (2nd ed.), Somerville, Mass.: International Press of Boston, ISBN 978-1571461377- Konta osobiste w Atiyah , Bott , Hirzebruch i Singer .
Zewnętrzne linki
Linki do teorii
- Mazzeo, Rafe. „Twierdzenie Atiyah-Singer Index: Co to jest i dlaczego powinno Cię to obchodzić” (PDF) . Zarchiwizowane z oryginału (PDF) 10 października 2002 r. Prezentacja w formacie PDF.
- Wojschechowski, MI; Shubin, MA (2001) [1994], "Wzory indeksowe" , Encyklopedia Matematyki , EMS Press
- Wassermann, Antoniusz . „Notatki z wykładów na temat twierdzenia o indeksie Atiyaha-Singera” . Zarchiwizowane z oryginału 29 marca 2017 r.
Linki do wywiadów
- Raussena, Martina; Skau, Christian (2005), „Wywiad z Michaelem Atiyah i Isadore Singer” (PDF) , Zawiadomienia o AMS , s. 223-231
- RR Seeley i inni (1999) Wspomnienia z początków teorii indeksów i operatorów pseudodyferencjalnych – częściowy zapis nieformalnej rozmowy po obiedzie podczas sympozjum, które odbyło się w Roskilde, Dania, we wrześniu 1998.














![{\ Displaystyle \ nazwa operatora {ch} (D) \ nazwa operatora {Td} (X) [X] = \ int _ {X} \ nazwa operatora {ch} (D) \ nazwa operatora {Td} (X)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5047dfe347066ec21a7204bafb29b1da0b5e5029)















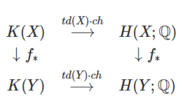





![{\ Displaystyle {\ textrm {indeks}} (D) = {\ textrm {ch}} (V) \ {\ textrm {Td}} (X) [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88e47901dd14e82003ddb14f3be0c73530614911)




