Maksymalny problem z podtablicą - Maximum subarray problem

Wizualizacja zmiany podtablic na podstawie pozycji początkowej i końcowej próbki. Każda możliwa ciągła podtablica jest reprezentowana przez punkt na kolorowej linii. Współrzędna y tego punktu reprezentuje sumę próbki. Jego współrzędna x reprezentuje koniec próbki, a skrajny lewy punkt tej kolorowej linii reprezentuje początek próbki. W tym przypadku tablica, z której pobierane są próbki to [2, 3, -1, -20, 5, 10].

W informatyce , maksymalna suma subarray problemem jest zadaniem znalezienia ciągłą subarray z największą sumą, w ramach danego jednowymiarowej tablicy A [1 ... n] liczb. Formalnie zadaniem jest znalezienie indeksów i z , tak aby suma $i$ ${\ Displaystyle j}$ $1\leq i\leq j\leq n$

{\ Displaystyle \ suma _ {x = i} ^ {j} A [x]}

jest jak największy. (Niektóre sformułowania problemu pozwalają również na uwzględnienie pustej podtablicy; umownie suma wszystkich wartości pustej podtablicy wynosi zero). Każda liczba w tablicy wejściowej A może być dodatnia, ujemna lub zerowa.

Na przykład dla tablicy wartości [-2, 1, -3, 4, -1, 2, 1, -5, 4] ciągła podtablica o największej sumie to [4, -1, 2, 1] , z sumą 6.

Niektóre właściwości tego problemu to:

Jeśli tablica zawiera wszystkie liczby nieujemne, problem jest trywialny; maksymalna podtablica to cała tablica.
Jeśli tablica zawiera wszystkie liczby niedodatnie, to rozwiązaniem jest dowolna podtablica o rozmiarze 1 zawierająca maksymalną wartość tablicy (lub pusta podtablica, jeśli jest to dozwolone).
Kilka różnych podtablic może mieć taką samą sumę maksymalną.

Ten problem można rozwiązać za pomocą kilku różnych technik algorytmicznych, w tym brutalnej siły, dziel i rządź, programowania dynamicznego i redukcji do najkrótszych ścieżek.

Historia

Problem maksymalnej podmacierzy został zaproponowany przez Ulfa Grenandera w 1977 roku jako uproszczony model do szacowania maksymalnego prawdopodobieństwa wzorców w zdigitalizowanych obrazach.

Grenander szukał prostokątnej podtablicy z sumą maksymalną w dwuwymiarowej tablicy liczb rzeczywistych. Algorytm siłowy dla zagadnienia dwuwymiarowego działa w czasie O ( n ⁶ ); ponieważ było to zbyt powolne, Grenander zaproponował jednowymiarowy problem, aby uzyskać wgląd w jego strukturę. Grenander wyprowadził algorytm, który rozwiązuje problem jednowymiarowy w czasie O ( n ² ), poprawiając czas działania brutalnej siły O ( n ³ ). Kiedy Michael Shamos usłyszał o problemie, z dnia na dzień opracował dla niego algorytm dziel i zwyciężaj O ( n log n ) . Niedługo potem Shamos opisał jednowymiarowy problem i jego historię na seminarium Carnegie Mellon University, w którym uczestniczył Jay Kadane , który w ciągu minuty zaprojektował algorytm O ( n )-czasu, który jest tak szybki, jak to tylko możliwe. W 1982 roku David Gries uzyskał ten sam algorytm czasu O ( n ) przez zastosowanie „strategii standardowej” Dijkstry ; w 1989 roku Richard Bird wyprowadził go przez czysto algebraiczne manipulowanie algorytmem siłowym przy użyciu formalizmu Birda-Meertensa .

Dwuwymiarowe uogólnienie Grenandera można rozwiązać w czasie O( n ³ ) albo używając algorytmu Kadane'a jako podprogramu, albo stosując podejście dziel i zwyciężaj. Nieco szybsze algorytmy oparte na mnożeniu macierzy odległości zaproponowali Tamaki i Tokuyama (1998) oraz Takaoka (2002) . Istnieją dowody na to, że nie istnieje znacznie szybszy algorytm; algorytm, który rozwiązuje dwuwymiarowy problem maksymalnej podtablicy w czasie O( n ^3-ε ), dla dowolnego ε>0, sugerowałby podobnie szybki algorytm dla problemu wszystkich par najkrótszych ścieżek .

Aplikacje

W wielu dziedzinach, takich jak analiza sekwencji genomowej i widzenie komputerowe, pojawiają się maksymalne problemy z podmacierzami .

Analiza sekwencji genomowej wykorzystuje maksymalne algorytmy podmacierzy do identyfikacji ważnych biologicznych segmentów sekwencji białkowych. Problemy te obejmują konserwatywne segmenty, regiony bogate w GC, powtórzenia tandemowe, filtr o niskiej złożoności, domeny wiążące DNA i regiony o wysokim ładunku.

W wizji komputerowej algorytmy maksymalnej podtablicy są używane na obrazach bitmapowych w celu wykrycia najjaśniejszego obszaru obrazu.

Algorytm Kadane

Dopuszczone puste podtablice

Przykładowy przebieg
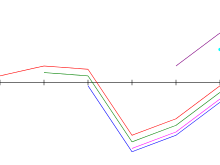
Wykonanie algorytmu Kadane na powyższej przykładowej tablicy. Niebieski : podtablica z największą sumą kończącą się na i ; zielony : podtablica z największą dotychczas napotkaną sumą; mała litera oznacza pustą tablicę; zmienna i pozostaje niejawna w kodzie Pythona.

Oryginalny algorytm Kadane'a rozwiązuje wersję problemu, gdy dopuszczane są puste podtablice. Skanuje daną tablicę od lewej do prawej. W kroku tym oblicza podtablicę z największą sumą kończącą się na ; suma ta jest utrzymywana w zmiennej . Co więcej, oblicza podtablicę z największą sumą w dowolnym miejscu w , utrzymywaną w zmiennej i łatwo uzyskaną jako maksimum wszystkich wartości widzianych do tej pory, por. wiersz 7 algorytmu. $A[1\ldots n]$ ${\ Displaystyle j}$ ${\ Displaystyle j}$ current_sum $A[1\ldots j]$ best_sumcurrent_sum

Jako niezmiennik pętli , w kroku th stara wartość zawiera maksimum nad całą sumą . W związku z tym jest to maksimum nad całą sumą . Aby rozszerzyć to ostatnie maksimum, aby objąć również przypadek , wystarczy wziąć pod uwagę również pustą podtablicę . Odbywa się to w linii 6, przypisując jako nową wartość , która następnie zawiera maksimum nad całą sumą . ${\ Displaystyle j}$ current_sum ${\ Displaystyle i \ w \ {1, \ ldots, j \}}$ $A[i]+\cdots +A[j-1]$ current_sum $+A[j]$ ${\ Displaystyle i \ w \ {1, \ ldots, j \}}$ ${\ Displaystyle A [i] + \ cdots + A [j]}$ $i=j+1$ $A[j+1\;\ldots \;j]$ $\max(0,$ current_sum $+A[j])$ current_sum ${\ Displaystyle i \ w \ {1, \ ldots, j + 1 \}}$ ${\ Displaystyle A [i] + \ cdots + A [j]}$

Tak więc problem można rozwiązać za pomocą następującego kodu, wyrażonego tutaj w Pythonie :

def max_subarray(numbers):
    """Find the largest sum of any contiguous subarray."""
    best_sum = 0  # or: float('-inf')
    current_sum = 0
    for x in numbers:
        current_sum = max(0, current_sum + x)
        best_sum = max(best_sum, current_sum)
    return best_sum

Ta wersja algorytmu zwróci 0, jeśli dane wejściowe nie zawierają elementów dodatnich (w tym, gdy dane wejściowe są puste).

Nie dopuszcza się pustych podtablic

Dla wariantu problemu, który nie zezwala na puste podtablice, best_sumnależy zamiast tego zainicjalizować ujemną nieskończoność, a także w pętli for current_sumnależy zaktualizować jako max(x, current_sum + x). W takim przypadku, jeśli dane wejściowe nie zawierają elementu dodatniego, zwracana jest wartość największego elementu (tj. wartość najbliższa 0) lub ujemna nieskończoność, jeśli dane wejściowe były puste.

Obliczanie najlepszej pozycji podtablicy

Algorytm można modyfikować, aby śledzić indeks początkowy i końcowy maksymalnej podtablicy:

def max_subarray(numbers):
    """Find a contiguous subarray with the largest sum."""
    best_sum = 0  # or: float('-inf')
    best_start = best_end = 0  # or: None
    current_sum = 0
    for current_end, x in enumerate(numbers):
        if current_sum <= 0:
            # Start a new sequence at the current element
            current_start = current_end
            current_sum = x
        else:
            # Extend the existing sequence with the current element
            current_sum += x

        if current_sum > best_sum:
            best_sum = current_sum
            best_start = current_start
            best_end = current_end + 1  # the +1 is to make 'best_end' exclusive

    return best_sum, best_start, best_end

W Pythonie tablice są indeksowane od 0, a indeks końcowy jest zazwyczaj wykluczony, więc podtablica [22, 33] w tablicy [-11, 22, 33, -44] zaczynałaby się od indeksu 1 i kończyła na indeksie 3.

Złożoność

Ze względu na sposób, w jaki algorytm ten wykorzystuje optymalne podstruktury (maksymalna podtablica kończąca się na każdej pozycji jest obliczana w prosty sposób z powiązanego, ale mniejszego i nakładającego się podproblemu: maksymalna podtablica kończąca się na poprzedniej pozycji) algorytm ten może być postrzegany jako prosty/ trywialny przykład programowania dynamicznego .

Złożoność uruchomieniowa algorytmu Kadane to . ${\ Displaystyle O (n)}$

Uogólnienia

Podobne problemy mogą pojawić się w przypadku tablic wielowymiarowych, ale ich rozwiązania są bardziej skomplikowane; patrz np. Takaoka (2002) . Brodal i Jørgensen (2007) pokazali, jak znaleźć k największych sum podtablic w jednowymiarowej tablicy, w optymalnym ograniczeniu czasowym . ${\ Displaystyle O (n + k)}$

Maksymalna suma k- rozłącznych podtablic może być również obliczona w optymalnym ograniczeniu czasowym . ${\ Displaystyle O (n + k)}$

Zobacz też

Problem sum podzbiorów

Uwagi

Bibliografia

Backurs, Arturs; Dikkala, Nishanth; Tzamos, Christos (2016), „Wąskie wyniki twardości dla prostokątów o maksymalnej masie”, Proc. 43. Międzynarodowe Kolokwium z Automatów, Języków i Programowania : 81:1–81:13, doi : 10.4230/LIPics.ICALP.2016.81 , S2CID 12720136
Bae, Sung Eun (2007), Sequential and Parallel Algorithms for the Generalized Maximum Subarray Problem (PDF) (praca doktorska), University of Canterbury, S2CID 2681670 , zarchiwizowane z oryginału (PDF) w dniu 26.10.2017.
Bengtsson, Fredrik; Chen, Jingsen (2007), Computing maximum scoring segments optimumly (PDF) (raport z badań), Luleå University of Technology
Bentley, Jon (1984), "Perły programowania: Algorytm techniki projektowania", Komunikacja ACM , 27 (9): 865-873, doi : 10.1145/358234.381162 , S2CID 207565329
Bentley, Jon (maj 1989), Perły programowania (wyd. 2?), Reading, MA: Addison Wesley, ISBN 0-201-10331-1
Bird, Richard S. (1989), "Tożsamości algebraiczne do obliczania programu" (PDF) , The Computer Journal , 32 (2): 122-126, doi : 10.1093/comjnl/32.2.122
Brodal, Gerth Stølting; Jørgensen, Allan Grønlund (2007), „Algorytm czasu liniowego dla problemu sum k maksymalnych”, Matematyczne podstawy informatyki , Wykład Notatki z informatyki , 4708 , Springer-Verlag, pp 442-453, doi : 10.1007/978 -3-540-74456-6_40.
Gries, David (1982), „Uwaga na temat standardowej strategii rozwoju niezmienników i pętli pętli” (PDF) , Nauka o programowaniu komputerowym , 2 (3): 207-241, doi : 10.1016/0167-6423(83)90015 -1 , hdl : 1813/6370
Takaoka, Tadao (2002), „Wydajne algorytmy dla maksymalnego problemu podtablicy przez mnożenie macierzy odległości”, Electronic Notes in Theoretical Computer Science , 61 : 191-200, doi : 10.1016/S1571-0661 (04) 00313-5.
Tamaki, Hisao; Tokuyama, Takeshi (1998), „Algorytmy dla maksymalnego problemu podtablicy w oparciu o mnożenie macierzy” , Proceedings of 9. Symposium on Discrete Algorithms (SODA) : 446-452 , pobrane 17 listopada 2018

Zewnętrzne linki

TAN, Lirong. „Problemy dotyczące maksymalnej liczby ciągłej podtablicy” (PDF) . Zarchiwizowane z oryginału (PDF) w dniu 2015-10-10 . Pobrano 26.10.2017 .
Mu, Shin-Cheng (2010). „Problem maksymalnej sumy segmentów: jego pochodzenie i wyprowadzenie” .
„Uwagi dotyczące maksymalnego problemu podtablic” . 2012.
www.algorytmist.com
alexeigor.wikidot.com
największy problem sumy następczej na kodzie Rosetty
Strona geeksforgeeks o algorytmie Kadane'a

Languages

In other projects