Dystrybucja Lévy'ego - Lévy distribution

Lévy (nieprzesunięty)

Funkcja gęstości prawdopodobieństwa
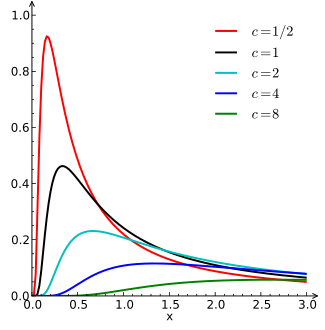Dystrybuanta
Parametry	${\ Displaystyle \ mu}$Lokalizacja; skala${\displaystyle c>0\,}$
Wsparcie	${\displaystyle x\in [\mu,\infty)}$
PDF	${\ Displaystyle {\ sqrt {\ Frac {c} {2 \ pi}}} ~ ~ {\ Frac {e ^ {- {\ Frac {c} {2 (x-\ mu)}}}} {(x -\mu )^{3/2}}}}$
CDF	${\ Displaystyle {\ textrm {erfc}} \ lewo ({\ sqrt {\ frac {c} {2 (x-\ mu)}}} \ prawej)}$
Mieć na myśli	${\displaystyle \infty}$
Mediana	${\ Displaystyle \ mu + c / 2 ({\ textrm {erfc}} ^ {-1} (1/2)) ^ {2} \,}$
Tryb	${\ Displaystyle \ mu + {\ Frac {c} {3}}}$
Zmienność	${\displaystyle \infty}$
Skośność	nieokreślony
Były. kurtoza	nieokreślony
Entropia	${\ Displaystyle {\ Frac {1 + 3 \ gamma + \ ln (16 \ pi c ^ {2})} {2}}}$ gdzie jest stała Eulera-Mascheroni${\ Displaystyle \ gamma}$
MGF	nieokreślony
CF	${\ Displaystyle e ^ {i \ mu t-{\ sqrt {-2 ict}}}}$

W teorii prawdopodobieństwa i statystyki , dystrybucja Lévy , nazwany Paul Lévy , to ciągły rozkład prawdopodobieństwa dla nieujemnej zmiennej losowej . W spektroskopii rozkład ten, z częstotliwością jako zmienną zależną, jest znany jako profil van der Waalsa . Jest to szczególny przypadek rozkładu odwrotnego gamma . Jest to stabilna dystrybucja .

Definicja

Funkcja gęstości prawdopodobieństwa rozkładu Lévy'ego w dziedzinie to ${\displaystyle x\geq\mu}$

${\ Displaystyle f (x; \ mu, c) = {\ sqrt {\ Frac {c} {2 \ pi}}} ~ ~ {\ Frac {e ^ {- {\ Frac {c} {2 (x- \mu )}}}}{(x-\mu )^{3/2}}}}$

gdzie jest parametrem lokalizacji i jest parametrem skali . Funkcja dystrybucji skumulowanej to ${\ Displaystyle \ mu}$${\displaystyle c}$

${\ Displaystyle F (x; \ mu, c) = {\ textrm {erfc}} \ lewo ({\ sqrt {\ Frac {c} {2 (x-\ mu)}}} \ prawej) = 2-2 \Phi \left({\sqrt {\frac {c}{(x-\mu )}}}\right)}$

gdzie jest komplementarną funkcją błędu i jest funkcją Laplace'a (CDF standardowego rozkładu normalnego). Parametr przesunięcia powoduje przesunięcie krzywej w prawo o wielkość , oraz zmianę wsparcia na przedział [ , ). Podobnie jak wszystkie dystrybucje stabilne , rozkład Levy'ego ma standardową postać f(x;0,1), która ma następującą właściwość: ${\displaystyle {\textrm {erfc}}(z)}$${\ Displaystyle \ Phi (x)}$${\ Displaystyle \ mu}$${\ Displaystyle \ mu}$${\ Displaystyle \ mu}$${\displaystyle \infty}$

${\displaystyle f(x;\mu,c)dx=f(y;0,1)dy\,}$

gdzie y jest zdefiniowane jako

${\ Displaystyle y = {\ Frac {x-\ mu} {c}} \}$

Funkcja charakterystyczna rozkładu opłaty jest podaje

${\ Displaystyle \ varphi (t; \ mu, c) = e ^ {i \ mu t-{\ sqrt {-2 ict}}}.}$

Zauważ, że funkcja charakterystyczna może być również zapisana w tej samej postaci, co w przypadku rozkładu stabilnego z i : ${\ Displaystyle \ alfa = 1/2}$${\ Displaystyle \ beta =1}$

${\ Displaystyle \ varphi (t; \ mu, c) = e ^ {i \ mu t-| ct | ^ {1/2} ~ (1-i ~ {\ textrm {znak}} (t))}. }$

Zakładając , n- ty moment nieprzesuniętego rozkładu Lévy'ego jest formalnie określony przez: ${\ Displaystyle \ mu = 0}$

${\ Displaystyle m_ {n} \ {\ stackrel {\ operatorname {def}} {=}} \ {\ sqrt {\ frac {c} {2 \ pi}}} \ int _ {0} ^ {\ infty} {\frac {e^{-c/2x}\,x^{n}}{x^{3/2}}}\,dx}$

która jest rozbieżna dla wszystkich, tak że momenty całkowite rozkładu Lévy'ego nie istnieją (tylko niektóre momenty ułamkowe). ${\displaystyle n\geq 0,5}$

Funkcja generująca moment byłaby formalnie zdefiniowana przez:

${\ Displaystyle M (t; c) \ {\ stackrel {\ operatorname {def}} {=}} \ {\ sqrt {\ frac {c} {2 \ pi}}} \ int _ {0} ^ {\ infty }{\frac {e^{-c/2x+tx}}{x^{3/2}}}\,dx}$

jednak jest to rozbieżne i dlatego nie jest zdefiniowane w przedziale wokół zera, więc funkcja generująca moment nie jest zdefiniowana per se . ${\displaystyle t>0}$

Podobnie jak wszystkie rozkłady stabilne, z wyjątkiem rozkładu normalnego , skrzydło funkcji gęstości prawdopodobieństwa wykazuje zachowanie się ciężkiego ogona odpadające zgodnie z prawem potęgowym:

${\displaystyle f(x;\mu,c)\sim {\sqrt {\frac {c}{2\pi}}}{\frac {1}{x^{3/2}}}}$   jak   ${\displaystyle x\do \infty,}$

co pokazuje, że Lévy jest nie tylko gruboogonem, ale także gruboogonem . To zilustrowano na poniższym schemacie, w którym funkcje gęstości prawdopodobieństwa dla różnych wartości C i nanosi się na wykresie podwójnie logarytmicznym . ${\ Displaystyle \ mu = 0}$

Funkcja gęstości prawdopodobieństwa dla rozkładu Lévy'ego na wykresie logarytmicznym

Standardowy rozkład Lévy'ego spełnia warunek stabilności

${\ Displaystyle (X_ {1} + X_ {2} + \ kropki + X_ {n}) \ SIM n ^ {1} \ alfa} X}$,

gdzie są niezależnymi standardowymi zmiennymi Lévy'ego z . ${\displaystyle X_{1},X_{2},\ldots,X_{n},X}$${\ Displaystyle \ alfa = 1/2}$

Powiązane dystrybucje

• Jeśli wtedy${\ Displaystyle X \, \ sim \, {\ textrm {opłata}} (\ mu, c)}$${\ Displaystyle kX + b \ \ sim \ {\ textrm {opłata}} (k \ mu + b, kc)}$
• Jeśli wtedy ( odwrotny rozkład gamma ) Tutaj rozkład Lévy'ego jest szczególnym przypadkiem rozkładu Pearsona typu V${\ Displaystyle X \, \ sim \, {\ textrm {opłata}} (0, c)}$${\ Displaystyle X \ \ Sim \ {\ textrm {Inv-Gamma}} ({\ tfrac {1} {2}}, {\ tfrac {c} {2}})}$
  
• Jeżeli ( Rozkład normalny ) to${\displaystyle \,Y\,\sim \{\textrm {normalny}}(\mu,\sigma)}$${\ Displaystyle {(Y-\ mu)} ^ {-2} \ \ sim \ {\ textrm {opłata}} (0,1/\ sigma ^ {2})}$
• Jeśli wtedy${\displaystyle X\,\sim \,{\textrm {normalny}}(\mu,{\tfrac {1}{\sqrt {\sigma}}})}$${\ Displaystyle {(X-\ mu)} ^ {-2} \ \ sim \ {\ textrm {opłata}} (0 \ sigma)}$
• Jeśli to ( dystrybucja stabilna )${\ Displaystyle X \, \ sim \, {\ textrm {opłata}} (\ mu, c)}$${\ Displaystyle X \, \ sim \, {\ textrm {stabilny}} (1/2, 1, c, \ mu)}$
• Jeśli to ( Rozkład skalowany-odwrotny-chi-kwadrat )${\ Displaystyle X \, \ sim \, {\ textrm {opłata}} (0, c)}$${\ Displaystyle X \ \ sim \ {\ textrm {Skala-inv}} \ chi ^ {2} (1, c)}$
• Jeśli tak ( Składany rozkład normalny )${\ Displaystyle X \, \ sim \, {\ textrm {opłata}} (\ mu, c)}$${\ Displaystyle {(X-\ mu)} ^ {- {\ tfrac {1} {2}}} \ sim \ {\ textrm {składany normalny}} (0,1/{\ sqrt {c}})}$

Generowanie próbek losowych

Próbki losowe z rozkładu Lévy'ego można generować przy użyciu próbkowania z transformacją odwrotną . Biorąc pod uwagę losową zmienną U wylosowaną z rozkładu jednostajnego na przedziale jednostkowym (0, 1], zmienna X dana przez

${\ Displaystyle X = F ^ {-1} (U) = {\ Frac {c} {(\ Phi ^ {-1} (1-U)) ^ {2}}} + \ mu}$

jest dystrybuowany przez Lévy'ego z lokalizacją i skalą . Oto skumulowana funkcja rozkładu standardowego rozkładu normalnego . ${\ Displaystyle \ mu}$${\displaystyle c}$${\ Displaystyle \ Phi (x)}$

Aplikacje

• Częstotliwość odwróceń geomagnetycznych wydaje się być zgodna z rozkładem Lévy'ego
• Czas trafiając jeden punkt, w odległości od punktu początkowego, przez ruchy Browna ma rozkład Levy z . (W przypadku ruchu Browna z dryftem, tym razem może być zgodny z odwrotnym rozkładem Gaussa , którego granicę stanowi rozkład Lévy'ego).${\ Displaystyle \ alfa}$${\ Displaystyle c = \ alfa ^ {2}}$
• Długość ścieżki, po której porusza się foton w mętnym ośrodku, jest zgodna z rozkładem Lévy'ego.
• Proces Cauchy- można zdefiniować jako Browna podporządkowaną do procesu związanego z rozkładem opłaty.

Przypisy

Uwagi

Bibliografia

• "Informacje o stabilnych dystrybucjach" . Źródło 5 września 2021 .- Wprowadzenie Johna P. Nolana do rozkładów stabilnych, kilka artykułów o prawach stabilnych oraz darmowy program do obliczania stałych gęstości, funkcji dystrybucji skumulowanej, kwantyli, estymacji parametrów itp. Zob. zwłaszcza Wprowadzenie do rozkładów stabilnych, rozdział 1

Zewnętrzne linki

• Weisstein, Eric W. „Dystrybucja Lévy'ego” . MatematykaŚwiat .