Granica funkcji - Limit of a function

Część serii artykułów o
Rachunek różniczkowy
Twierdzenie podstawowe integralna reguła Leibniza Granice funkcji Ciągłość Twierdzenie o wartości średniej Twierdzenie Rolle'a
Mechanizm różnicowy Definicje Pochodna  ( uogólnienia ) Mechanizm różnicowy nieskończenie mały funkcji całkowity Koncepcje Notacja różniczkowa Druga pochodna Niejawne zróżnicowanie Różnicowanie logarytmiczne Powiązane stawki Twierdzenie Taylora Zasady i tożsamości Suma Produkt Łańcuch Moc Iloraz Zasada L'Hôpital Odwrotność Generał Leibniz Formuła Faà di Bruno Reynoldsa
Całka Listy całek Transformacja całkowa Definicje Pochodna pierwotna Całka  ( niewłaściwa ) Całka Riemanna Integracja Lebesgue'a Integracja konturu Całka funkcji odwrotnych Integracja przez Części Dyski Cylindryczne muszle Podstawienie  ( trygonometryczne , Weierstrassa , Eulera ) Wzór Eulera Frakcje częściowe Zmiana kolejności Formuły redukcyjne Różniczkowanie pod znakiem całkowym Algorytm Richa
Seria Geometryczny  ( arytmetyczno-geometryczny ) Harmoniczny Zmienny Moc Dwumianowy Taylor Testy konwergencji Limit sumy (test terminowy) Stosunek Źródło Całka Bezpośrednie porównanie Porównanie limitów Seria naprzemienna Kondensacja Cauchy'ego Dirichlet Abel
Wektor Gradient Rozbieżność Kędzior Laplace'a Kierunkowa pochodna Tożsamości Twierdzenia Gradient Warzywa Stokesa Rozbieżność uogólniony Stokes
Wiele zmiennych Formalizmy Matryca Napinacz Zewnętrzny Geometryczny Definicje Częściowa pochodna Wielokrotna całka Całka liniowa Całka powierzchniowa Całka objętości Jakobian heski
Specjalistyczne Frakcyjny Maliavin Stochastyczny Wariacje
Różnorodny Wstępny rachunek różniczkowy Historia Słowniczek Lista tematów Pszczoła integracyjna Analiza
v T mi

W matematyce , granica funkcji jest podstawowym pojęciem w rachunku i analizy dotyczące zachowania tej funkcji pobliżu danego wejścia .

Poniżej podano formalne definicje, opracowane po raz pierwszy na początku XIX wieku. Nieformalnie funkcja f przypisuje dane wyjściowe f ( x ) do każdego wejścia x . Mówimy, że funkcja ma granicę L na wejściu p, jeśli f ( x ) zbliża się coraz bardziej do L, gdy x zbliża się coraz bardziej do p . Dokładniej, gdy f jest zastosowane do dowolnego wejścia wystarczająco blisko p , wartość wyjściowa jest wymuszona arbitralnie blisko L . Z drugiej strony, jeśli niektóre wejścia bardzo bliskie p zostaną przeniesione do wyjść, które pozostają w stałej odległości od siebie, wtedy mówimy, że granica nie istnieje .

Pojęcie granicy ma wiele zastosowań we współczesnym rachunku różniczkowym . W szczególności wiele definicji ciągłości posługuje się pojęciem granicy: z grubsza funkcja jest ciągła, jeśli wszystkie jej granice zgadzają się z wartościami funkcji. Pojęcie granicy pojawia się również w definicji pochodnych : na rachunku jednej zmiennej, to wartość graniczna na stoku od sieczna do wykresu funkcji.

Historia

Chociaż zakorzeniona w rozwoju rachunku różniczkowego w XVII i XVIII wieku, współczesna idea granicy funkcji sięga Bolzano, który w 1817 r. wprowadził podstawy techniki epsilon-delta w celu zdefiniowania funkcji ciągłych. Jednak jego twórczość nie była znana za jego życia.

W swojej książce Cours d'analyse z 1821 r. Cauchy omówił zmienne wielkości, nieskończenie małe i ograniczenia oraz zdefiniował ciągłość , mówiąc, że nieskończenie mała zmiana w x z konieczności powoduje nieskończenie małą zmianę w y , podczas gdy ( Grabiner 1983 ) twierdzi, że użył rygorystycznego epsilon -definicja delta w próbach. Weierstrass po raz pierwszy wprowadził definicję granicy epsilon-delta w formie, w jakiej jest ona dziś zapisywana. Wprowadził także oznaczenia lim i lim _{x → x 0} . ${\ Displaystyle y = f (x)}$

Współczesna notacja umieszczania strzałki poniżej symbolu limitu jest spowodowana przez Hardy'ego , który został wprowadzony w jego książce A Course of Pure Mathematics w 1908 roku.

Motywacja

Wyobraź sobie osobę idącą po krajobrazie reprezentowanym przez wykres y = f ( x ). Ich położenie w poziomie jest mierzone wartością x , podobnie jak położenie podane na mapie terenu lub przez globalny system pozycjonowania . Ich wysokość określa współrzędna y . Idą w kierunku pozycji poziomej określonej przez x = p . W miarę jak się do niej zbliżają, zauważają, że ich wysokość zbliża się do L . Zapytani o wysokość x = p , odpowiedzieliby L .

Co w takim razie oznacza stwierdzenie, że ich wysokość zbliża się do L? Oznacza to, że ich wysokość zbliża się coraz bardziej do L — z wyjątkiem możliwego małego błędu w dokładności. Załóżmy na przykład, że wyznaczyliśmy podróżnemu konkretny cel dokładności: musi on zbliżyć się do L . Zgłaszają, że rzeczywiście mogą zbliżyć się na dziesięć metrów w pionie od L , ponieważ zauważają, że gdy znajdują się w odległości pięćdziesięciu metrów w poziomie od p , ich wysokość zawsze wynosi dziesięć metrów lub mniej od L .

Cel dokładności zostaje wtedy zmieniony: czy mogą zbliżyć się do jednego pionowego metra? Tak. Jeśli znajdują się gdziekolwiek w promieniu siedmiu poziomych metrów od p , ich wysokość zawsze pozostanie w odległości jednego metra od celu L . Podsumowując, powiedzieć, że wysokość podróżnego zbliża się do L, gdy jego pozycja pozioma zbliża się do p , oznacza to, że dla każdego celu dokładności celu, jakkolwiek mały by on nie był, istnieje pewne sąsiedztwo p, którego wysokość spełnia ten cel dokładności.

Wstępne nieformalne oświadczenie można teraz wyjaśnić:

Granica funkcji f ( x ) w miarę zbliżania się x do p jest liczbą L o następującej własności: przy dowolnej odległości docelowej od L , istnieje odległość od p, w której wartości f ( x ) pozostają w odległości docelowej.

W rzeczywistości to wyraźne stwierdzenie jest dość bliskie formalnej definicji granicy funkcji z wartościami w przestrzeni topologicznej .

A dokładniej mówiąc, że

${\ Displaystyle \ lim _ {x \ do p} f (x) = L \,}$

to powiedzieć, że ƒ ( x ) może być tak blisko L, jak to pożądane, czyniąc x wystarczająco blisko, ale nie równym, do  p .

Poniższe definicje, znane jako (ε, δ)-definicje, są ogólnie przyjętymi definicjami granicy funkcji w różnych kontekstach.

Funkcje pojedynczej zmiennej

(ε, δ)-definicja granicy

Załóżmy, że f  : R → R jest zdefiniowane na prostej i p, L ∈ R . Można powiedzieć, że granica f , gdy x zbliża się do p , to L i napisane

${\ Displaystyle \ lim _ {x \ do p} f (x) = L}$

lub alternatywnie jako:

${\ Displaystyle f (x) \ do L}$jak (czyta „ ma tendencję do tego, jak ma tendencję do ”)${\displaystyle x\do p}$${\displaystyle f(x)}$${\ Displaystyle L}$${\displaystyle x}$${\displaystyle p}$

jeżeli następująca własność posiada:

• Dla każdego rzeczywistego ε > 0 , istnieje rzeczywisty δ > 0 taki, że dla wszystkich rzeczywistych x, 0 < | x − p | < δ oznacza, że | f ( x ) − L | < ε .

Bardziej ogólna definicja dotyczy funkcji zdefiniowanych na podzbiorach prostej rzeczywistej. Niech ( a ,  b ) będzie przedziałem otwartym w R , a p punktem ( a ,  b ). Niech f będzie funkcją o wartościach rzeczywistych zdefiniowaną na wszystkich ( a ,  b ) — z wyjątkiem być może samego p . Mówi się wtedy, że granica f, gdy x zbliża się do p, wynosi L, jeśli dla każdego rzeczywistego ε > 0 , istnieje rzeczywisty δ > 0 taki, że 0 < | x − p | < δ i x ∈ ( a , b ) implikuje , że | f ( x ) − L | < ε .

Zauważ, że wartość granicy nie zależy od zdefiniowania f w p , ani od wartości f ( p ) — jeśli jest zdefiniowana.

Litery ε i δ można rozumieć jako „błąd” i „odległość”. W rzeczywistości Cauchy użył ε jako skrótu od „błędu” w niektórych swoich pracach, chociaż w swojej definicji ciągłości użył raczej nieskończenie małej niż ε lub δ (patrz Cours d'Analyse ). W tych terminach błąd ( ε ) w pomiarze wartości na granicy może być tak mały, jak to pożądane, poprzez zmniejszenie odległości ( δ ) do punktu granicznego. Jak omówiono poniżej, ta definicja działa również w przypadku funkcji w bardziej ogólnym kontekście. Pomysł, że δ i ε reprezentują odległości, pomaga zasugerować te uogólnienia. ${\ Displaystyle \ alfa}$

Istnienie i jednostronne granice

Alternatywnie, x może zbliżyć się do p z góry (po prawej) lub poniżej (po lewej), w którym to przypadku granice mogą być zapisane jako

${\ Displaystyle \ lim _ {x \ do p ^ {+}} f (x) = L}$

lub

${\ Displaystyle \ lim _ {x \ do p ^ {-}} f (x) = L}$

odpowiednio. Jeżeli te granice istnieją P i nie są równe, to może to być nazywane w granicach f ( x ) w p . Jeśli jednostronne granice istnieją w p , ale są nierówne, to nie ma granicy w p (tj. granica w p nie istnieje). Jeśli którakolwiek z jednostronnych granic nie istnieje w p , to granica w p również nie istnieje.

Formalna definicja jest następująca. Granica f ( x ) gdy x zbliża się do p z góry wynosi L, jeśli dla każdego ε  > 0 istnieje δ > 0 takie, że | f ( x ) −  L | <  ε gdy 0 <  x  −  p  <  δ . Granica f ( x ) przy x zbliżającym się do p od dołu wynosi L, jeśli dla każdego ε > 0 istnieje δ > 0 takie, że | f ( x ) −  L | <  ε gdy 0 <  p  −  x  <  δ .

Jeśli granica nie istnieje, to oscylacje o f u p jest różny od zera.

Bardziej ogólne podzbiory

Poza przedziałami otwartymi, granice mogą być określone dla funkcji na dowolnych podzbiorach R w następujący sposób ( Bartle & Sherbert 2000 ) : niech f będzie funkcją o wartościach rzeczywistych zdefiniowaną na podzbiorze S linii rzeczywistej. Niech t będzie punktu granicznego z S -to jest P jest granica niektórych sekwencji elementów S odróżnieniu od str. Granica f , gdy x zbliża się do p od wartości w S , wynosi L , jeśli dla każdego ε > 0 , istnieje δ > 0 takie, że 0 < | x − p | < δ i x ∈ S implikuje, że | f ( x ) − L | < ε . błąd harv: brak celu: CITEREFBartleSherbert2000 ( pomoc )

Ten limit jest często zapisywany jako:

${\ Displaystyle L = \ lim _ {\ stos {x \ do p} {x \ w S}} f (x).}$

Warunkiem zdefiniowania f na S jest to, że S będzie podzbiorem dziedziny f . To uogólnienie obejmuje jako specjalne przypadki granice przedziału, jak również lewoskrętne granice funkcji o wartościach rzeczywistych (np. przyjmując S za otwarty przedział postaci ) i prawostronne granice (np. biorąc S być otwartym przedziałem formularza ). Rozszerza również pojęcie granic jednostronnych na zawarte punkty końcowe przedziałów (pół-)zamkniętych, więc funkcja pierwiastka kwadratowego f ( x )= √ x może mieć granicę 0, gdy x zbliża się do 0 z góry. ${\displaystyle (-\infty ,a)}$${\displaystyle (a,\infty)}$

Usunięte a nieusunięte limity

Podana tutaj definicja granicy nie zależy od tego, jak (lub czy) f jest zdefiniowane w p . Bartle (1967) określa to jako granicę usuniętą , ponieważ wyklucza ona wartość f na p . Odpowiednia nieusunięta granica zależy od wartości f w p , jeśli p należy do dziedziny f :

• Liczba L jest nieusuniętą granicą f, gdy x zbliża się do p, jeśli dla każdego ε > 0 istnieje δ > 0 takie, że | x  −  p  | <  δ i x ∈ Dm ( f ) implikuje | f ( x ) −  L  | <  ε .

Definicja jest taka sama, z tym wyjątkiem, że sąsiedztwo | x  −  p  | <  δ zawiera teraz punkt p , w przeciwieństwie do usuniętego otoczenia 0 < | x  −  p  | <  Δ . To sprawia, że ​​definicja nieusuniętego limitu jest mniej ogólna. Jedną z zalet pracy z nieusuniętymi granicami jest to, że pozwalają one na sformułowanie twierdzenia o granicach kompozycji bez żadnych ograniczeń dotyczących funkcji (innych niż istnienie ich nieusuniętych granic) ( Hubbard (2015) ).

Bartle (1967) zauważa, że ​​chociaż niektórzy autorzy przez „limit” mają na myśli ten nieusunięty limit, najbardziej popularne są limity usunięte. Na przykład Apostol (1974) , Courant (1924) , Hardy (1921) , Rudin (1964) , Whittaker i Watson (1902) rozumieją „limit” jako usuniętą granicę. błąd harvtxt: brak celu: CITEREFWhittakerWatson1902 ( pomoc )

Przykłady

Brak ograniczeń jednostronnych

Funkcja

${\ Displaystyle f (x) = {\ zacząć {przypadki} \ grzech {\ Frac {5} {x-1}} i {\ tekst {dla}} x <1 \ \ 0 i {\ tekst { dla}} x =1\\{\frac {0.1}{x-1}}&{\text{ dla }}x>1\end{przypadków}}}$

nie ma limitu ( granica po lewej stronie nie istnieje ze względu na oscylacyjny charakter funkcji sinus, a granica po prawej stronie nie istnieje ze względu na asymptotyczne zachowanie funkcji odwrotnej), ale ma granicę na każdym innym x -współrzędna. ${\displaystyle x_{0}=1}$

Funkcja

${\ Displaystyle f (x) = {\ zacząć {przypadki} 1 i x {\ tekst {racjonalne}} \ \ 0 i x {\ tekst { irracjonalne}} \ koniec {przypadki}}}$

(inaczej funkcja Dirichleta ) nie ma limitu na żadnej współrzędnej x .

Nierówność granic jednostronnych

Funkcja

${\ Displaystyle f (x) = {\ zacząć {przypadki} 1 i {\ tekst {dla}} x <0 \ \ 2 i {\ tekst { dla}} x \ geq 0 \ koniec {przypadki}}}$

ma limit na każdej niezerowej współrzędnej x (limit wynosi 1 dla ujemnego x i 2 dla dodatniego x ). Granica przy x = 0 nie istnieje (granica po lewej stronie wynosi 1, podczas gdy granica po prawej stronie wynosi 2).

Ograniczenia tylko w jednym punkcie

Funkcje

${\ Displaystyle f (x) = {\ zacząć {przypadki} x i x {\ tekst {racjonalne}} \ \ 0 i x {\ tekst { irracjonalne}} \ koniec {przypadki}}}$

oraz

${\ Displaystyle f (x) = {\ zacząć {przypadki} | x | x {\ tekst {racjonalne}} \ \ 0 i x {\ tekst { irracjonalne}} \ koniec {przypadki}}}$

oba mają limit na x = 0 i jest równy 0.

Limity w policzalnie wielu punktach

Funkcja

${\ Displaystyle f (x) = {\ zacząć {przypadki} \ grzech x i x {\ tekst {nieracjonalne}} \ \ 1 i x {\ tekst { racjonalne}} \ koniec {przypadki}}}$

ma limit na dowolnej współrzędnej x postaci , gdzie n jest dowolną liczbą całkowitą. ${\displaystyle {\frac {\pi}{2}}+2n\pi}$

Funkcje na przestrzeniach metrycznych

Załóżmy, M i N są podzbiorami przestrzeni metrycznych A i B , odpowiednio, i f  : M → N jest określona pomiędzy M i N , a x ∈ m, p punktu granicznego z M i L ∈ N . Mówi się, że granica f, gdy x zbliża się do p, to L i napisz

${\ Displaystyle \ lim _ {x \ do p} f (x) = L}$

jeżeli następująca własność posiada:

• Dla każdego ε > 0 istnieje δ > 0 takie, że d _B ( f ( x ), L ) < ε gdy 0 <  d _A ( x ,  p ) <  δ .

Ponownie zauważ, że p nie musi należeć do dziedziny f , ani L nie musi należeć do zakresu f , a nawet jeśli f ( p ) jest zdefiniowane, nie musi być równe L .

Alternatywna definicja wykorzystująca pojęcie sąsiedztwa jest następująca:

${\ Displaystyle \ lim _ {x \ do p} f (x) = L}$

jeśli dla każdego otoczenia V z L w B , istnieje takie otoczenie U z p w A , że f (U ∩ M − { p }) ⊆ V .

Funkcje na przestrzeniach topologicznych

Załóżmy, że X , Y są topologiczne przestrzenie z Y przestrzeni Hausdorff . Niech p będzie punktem granicznym Ω ⊆  X , a L ∈ Y . Dla funkcji f  : Ω → Y , mówi się, że granica f gdy x zbliża się do p wynosi L (tj. f ( x ) → L jak x → p ) i zapisana

${\ Displaystyle \ lim _ {x \ do p} f (x) = L}$

jeżeli następująca własność posiada:

• Dla każdego otwartego sąsiedztwa V elementu L istnieje otwarte otoczenie U elementu p takie, że f ( U  ∩ Ω − { p } ) ⊆ V .

Ta ostatnia część definicji może być również sformułowana „istnieje otwarte przebite sąsiedztwo U z p takie, że f ( U ∩Ω) ⊆ V ”.

Zauważ, że dziedzina f nie musi zawierać p . Jeśli tak, to wartość f w p jest nieistotna dla definicji granicy. W szczególności, jeśli dziedziną f jest X  − { p } (lub całe X ), wtedy granica f jako x → p istnieje i jest równa L jeśli dla wszystkich podzbiorów Ω X z punktem granicznym p , granica ograniczenia f do Ω istnieje i jest równa L . Czasami to kryterium jest używane do ustalenia nieistnienia granicy dwustronnej funkcji na R poprzez pokazanie, że granice jednostronne albo nie istnieją, albo nie są zgodne. Taki pogląd jest fundamentalny w dziedzinie ogólnej topologii , gdzie granice i ciągłość w punkcie są definiowane w kategoriach specjalnych rodzin podzbiorów, zwanych filtrami , lub uogólnionych ciągów zwanych sieciami .

Alternatywnie, wymaganie, aby Y była przestrzenią Hausdorffa, można rozluźnić do założenia, że Y jest ogólną przestrzenią topologiczną, ale wtedy granica funkcji może nie być jednoznaczna. W szczególności nie można już mówić o granicy funkcji w punkcie, ale o granicy lub zbiorze granic w punkcie.

Funkcja jest ciągły w punkcie granicy p i w dziedzinie, jeżeli i tylko jeżeli f ( P ) jest (lub, w ogólnym przypadku, ) Granica f ( x ) w postaci X zwykle p .

Granice obejmujące nieskończoność

Granice w nieskończoności

Niech , i . ${\ Displaystyle S \ podseteq \ mathbb {R}}$${\ Displaystyle x \ w S}$${\ Displaystyle f: S \ mapsto \ mathbb {R}}$

Granica f, gdy x zbliża się do nieskończoności, to L , oznaczone

${\ Displaystyle \ lim _ {x \ do \ infty} f (x) = L}$

oznacza, że ​​dla wszystkich istnieje c takie, że zawsze , gdy x  >  c . Lub symbolicznie: ${\ Displaystyle \ varepsilon > 0}$${\ Displaystyle | f (x)-L | <\ varepsilon }$

${\displaystyle \forall \varepsilon>0\;\istnieje c\;\forall x>c:\;|f(x)-L|<\varepsilon}$.

Podobnie, granica f gdy x zbliża się do ujemnej nieskończoności to L , oznaczane

${\ Displaystyle \ lim _ {x \ do - \ infty} f (x) = L}$

oznacza, że ​​dla wszystkich istnieje c takie, że gdy x  <  c . Lub symbolicznie: ${\ Displaystyle \ varepsilon > 0}$${\ Displaystyle | f (x)-L | <\ varepsilon }$

${\displaystyle \forall \varepsilon>0\;\istnieje c\;\forall x<c:\;|f(x)-L|<\varepsilon}$.

Na przykład,

${\ Displaystyle \ lim _ {x \ do - \ infty} e ^ {x} = 0. \,}$

Nieskończone granice

Dla funkcji, której wartości rosną bez ograniczeń, funkcja jest rozbieżna i zwykła granica nie istnieje. Jednak w tym przypadku można wprowadzić limity o wartościach nieskończonych. Niech , i . Stwierdzenie, że granica f w miarę zbliżania się x do a jest nieskończonością , oznaczoną ${\ Displaystyle S \ podseteq \ mathbb {R}}$${\ Displaystyle x \ w S}$${\ Displaystyle f: S \ mapsto \ mathbb {R}}$

${\ Displaystyle \ lim _ {x \ do} f (x) = \ infty}$

oznacza, że ​​dla wszystkich istnieje takie, że kiedykolwiek${\ Displaystyle N> 0}$${\ Displaystyle \ delta > 0}$${\displaystyle f(x)>N}$${\displaystyle 0<|xa|<\delta.}$

Te pomysły można łączyć w naturalny sposób, tworząc definicje dla różnych kombinacji, takie jak

${\ Displaystyle \ lim _ {x \ do \ infty} f (x) = \ infty, \ lim _ {x \ do ^ {+}} f (x) = - \ infty.}$

Na przykład,

${\ Displaystyle \ lim _ {x \ do 0 ^ {+}} \ ln x = - \ infty.}$

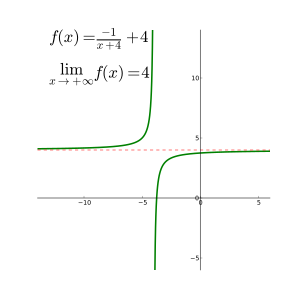
Granice obejmujące nieskończoność związane są z pojęciem asymptot .

Te pojęcia granicy próbują dostarczyć interpretacji przestrzeni metrycznej do granic w nieskończoności. W rzeczywistości są one zgodne z topologiczną definicją granicy if

• sąsiedztwo −∞ jest zdefiniowane tak, aby zawierało przedział [−∞,  c ) dla pewnego c  ∈  R ,
• sąsiedztwo ∞ jest zdefiniowane tak, aby zawierało przedział ( c , ∞] gdzie c  ∈  R , i
• otoczeniem a ∈ R jest zdefiniowana w normalny sposób przestrzeń metryczna R .

W tym przypadku R jest przestrzenią topologiczną i każda funkcja postaci f :  X  →  Y gdzie X ,  Y ⊆  R podlega topologicznej definicji granicy. Należy zauważyć, że dzięki tej topologicznej definicji łatwo jest zdefiniować nieskończone granice w punktach skończonych, które nie zostały zdefiniowane powyżej w sensie metrycznym.

Notacja alternatywna

Wielu autorów pozwala na wykorzystanie projekcyjnie przedłużonej linii rzeczywistej jako sposobu na uwzględnienie wartości nieskończonych, jak również przedłużonej linii rzeczywistej . W tym zapisie rozszerzona prosta rzeczywista jest podana jako R ∪ {−∞, +∞}, a rozszerzona rzutowo prosta rzeczywista to R  ∪ {∞}, gdzie sąsiedztwo ∞ jest zbiorem postaci { x : | x | > c }. Zaletą jest to, że wystarczy tylko trzy definicje granic (lewy, prawy i środkowy), aby objąć wszystkie przypadki. Jak przedstawiono powyżej, dla całkowicie rygorystycznego rachunku musielibyśmy rozważyć 15 oddzielnych przypadków dla każdej kombinacji nieskończoności (pięć kierunków: −∞, lewy, środkowy, prawy i +∞; trzy granice: −∞, skończone lub + ). Istnieją również godne uwagi pułapki. Na przykład podczas pracy z rozszerzoną linią rzeczywistą nie ma centralnego limitu (co jest normalne): ${\ Displaystyle x ^ {-1}}$

${\ Displaystyle \ lim _ {x \ do 0 ^ {+}} {1 \ ponad x} = + \ infty \ lim _ {x \ do 0 ^ {-}} {1 \ ponad x} = - \ infty .}$

W przeciwieństwie do tego, podczas pracy z rzutowej rzeczywistej linii nieskończoności (podobnie jak 0) są podpisane, więc, centralny granica nie istnieje w tym kontekście:

${\ Displaystyle \ lim _ {x \ do 0 ^ {+}} {1 \ nad x} = \ lim _ {x \ do 0 ^ {-}} {1 \ nad x} = \ lim _ {x \ do 0}{1 \ponad x}=\infty .}$

W rzeczywistości w użyciu jest mnóstwo sprzecznych systemów formalnych. W niektórych zastosowaniach różniczkowania i całkowania numerycznego wygodnie jest mieć na przykład zera ze znakiem . Prosty powód ma związek z odwrotnością , a mianowicie wygodnie jest uważać go za prawdziwy. Takie zera mogą być postrzegane jako przybliżenie do nieskończenie małych . ${\ Displaystyle \ lim _ {x \ do 0 ^ {-}} {x ^ {-1}} = - \ infty}$${\ Displaystyle \ lim _ {x \ do - \ infty} {x ^ {-1}} = -0}$

Granice w nieskończoności dla funkcji wymiernych

Istnieją trzy podstawowe zasady oceny granic w nieskończoności dla funkcji wymiernej f ( x ) = p ( x )/ q ( x ): (gdzie p i q są wielomianami):

• Jeśli stopień z p jest większy niż stopień Q , to granica jest dodatnia lub ujemna w zależności od nieskończoności oznaczeń czołowych współczynników;
• Jeśli stopnie p i q są równe, granicą jest wiodący współczynnik p podzielony przez wiodący współczynnik q ;
• Jeśli stopień p jest mniejszy niż stopień q , granica wynosi 0.

Jeśli granica w nieskończoności istnieje, reprezentuje poziomą asymptotę w y = L . Wielomiany nie mają asymptot poziomych; takie asymptoty mogą jednak wystąpić w przypadku funkcji wymiernych.

Funkcje więcej niż jednej zmiennej

Zauważając, że | x  −  p | reprezentuje odległość, definicję granicy można rozszerzyć na funkcje więcej niż jednej zmiennej. W przypadku funkcji f  : R ² → R ,

${\ Displaystyle \ lim _ {(x, y) \ do (p, q)} f (x, y) = L}$

Jeśli

dla każdego ε > 0 istnieje δ > 0 takie , że dla wszystkich ( x , y ) z 0 < ||( x , y ) − ( p , q )|| < δ, to | f ( x , y ) −  L | < ε

gdzie ||( x , y ) − ( p , q )|| reprezentuje odległość euklidesową . Można to rozszerzyć na dowolną liczbę zmiennych.

Limity sekwencyjne

Niech f  : X → Y będzie odwzorowaniem z przestrzeni topologicznej X na przestrzeń Hausdorffa Y , p ∈ X będzie punktem granicznym X i L ∈ Y .

Sekwencyjnego ograniczenie od f a x ma tendencję do p wynosi L , jeżeli dla każdej sekwencji ( x _n ) w X - { s } , która zbiega się do P , sekwencja f ( x _n ) zbieżny do L .

Jeśli L jest granicą (w powyższym sensie) f, gdy x zbliża się do p , to jest to również granica sekwencyjna, jednak odwrotność nie musi mieć miejsca. Jeśli dodatkowo X jest metryzowalne , to L jest sekwencyjną granicą f, gdy x zbliża się do p wtedy i tylko wtedy, gdy jest to granica (w powyższym sensie) f, gdy x zbliża się do p .

Inne charakterystyki

Pod względem sekwencji

W przypadku funkcji na linii rzeczywistej jednym ze sposobów zdefiniowania granicy funkcji jest określenie granicy ciągów. (Ta definicja jest zwykle przypisywana Eduardowi Heine .) W tym ustawieniu:

${\ Displaystyle \ lim _ {x \ do} f (x) = L}$

wtedy i tylko wtedy, gdy dla wszystkich ciągów (z nie równym a dla wszystkich n ) zbiega się do ciągu zbiega się do . Jak pokazał Sierpiński w 1916 r., udowodnienie równoważności tej definicji i definicji powyżej wymaga i jest równoznaczne ze słabą formą aksjomatu wyboru . Zwróć uwagę, że zdefiniowanie, co to znaczy dla sekwencji, z którą ma być zbieżna, wymaga metody epsilon, delta . ${\displaystyle x_{n}}$${\displaystyle x_{n}}$${\displaystyle a}$${\ Displaystyle f (x_ {n})}$${\ Displaystyle L}$${\displaystyle x_{n}}$${\displaystyle a}$

Podobnie jak w przypadku definicji Weierstrassa, bardziej ogólna definicja Heinego dotyczy funkcji zdefiniowanych na podzbiorach prostej rzeczywistej. Niech f będzie funkcją o wartościach rzeczywistych z dziedziną Dm ( f ). Niech a będzie granicą ciągu elementów Dm ( f ) \ { a }. Wtedy granica (w tym sensie) f wynosi L gdy x zbliża się do p jeśli dla każdego ciągu  ∈  Dm ( f ) \ { a } (a więc dla wszystkich n , nie jest równe a ), który jest zbieżny do a , ciąg jest zbieżny do . Jest to to samo, co definicja sekwencyjnego limitu w poprzedniej sekcji, uzyskana przez traktowanie podzbioru Dm ( f ) R jako przestrzeni metrycznej z indukowaną metryką. ${\displaystyle x_{n}}$${\displaystyle x_{n}}$${\ Displaystyle f (x_ {n})}$${\ Displaystyle L}$

W rachunku niestandardowym

W rachunku niestandardowym granica funkcji jest określona przez:

${\ Displaystyle \ lim _ {x \ do} f (x) = L}$

wtedy i tylko wtedy, gdy dla wszystkich , jest nieskończenie małe zawsze, gdy jest nieskończenie małe. Tutaj są numery Hiperrzeczywista i jest naturalnym przedłużeniem f do niestandardowych liczb rzeczywistych. Keisler udowodnił, że taka hiperrzeczywista definicja granicy zmniejsza złożoność kwantyfikatora o dwa kwantyfikatory. Z drugiej strony Hrbacek pisze, że aby definicje były ważne dla wszystkich liczb hiperrzeczywistych muszą być domyślnie ugruntowane w metodzie ε-δ i twierdzi, że z pedagogicznego punktu widzenia nadzieja, że ​​nietypowy rachunek może być wykonane bez metod ε-δ nie mogą być zrealizowane w całości. Błaszczyk i in. szczegół przydatność microcontinuity rozwojem przezroczystą określenia jednolitej ciągłości i krytyczne Hrbáček scharakteryzować jako „wątpliwej lamentów”. ${\ Displaystyle x \ w \ mathbb {R} ^ {*}}$${\ Displaystyle f ^ {*} (x) -L}$${\displaystyle xa}$${\ Displaystyle \ mathbb {R} ^ {*}}$${\ Displaystyle f ^ {*}}$

Pod względem bliskości

Na Międzynarodowym Kongresie Matematyki w 1908 roku F. Riesz wprowadził alternatywny sposób określania granic i ciągłości w pojęciu zwanym „bliskość”. Punkt jest zdefiniowany w pobliżu zbioru, jeśli dla każdego istnieje punkt tak, że . W tym ustawieniu ${\displaystyle x}$${\ Displaystyle A \ podseteq \ mathbb {R}}$${\displaystyle r>0}$${\displaystyle a\w A}$${\displaystyle |xa|<r}$

${\ Displaystyle \ lim _ {x \ do} f (x) = L}$

wtedy i tylko wtedy, gdy dla wszystkich , jest blisko , gdy jest blisko . Oto zestaw . Tę definicję można również rozszerzyć na przestrzenie metryczne i topologiczne. ${\ Displaystyle A \ podseteq \ mathbb {R}}$${\ Displaystyle L}$${\displaystyle f(A)}$${\displaystyle a}$${\ Displaystyle A}$${\displaystyle f(A)}$${\ Displaystyle \ {f (x) | x \ w A \}}$

Związek z ciągłością

Pojęcie granicy funkcji jest bardzo ściśle związane z pojęciem ciągłości. Mówi się, że funkcja ƒ jest ciągła w c, jeśli jest zdefiniowana w c i jej wartość w c jest równa granicy f, gdy x zbliża się do c :

${\ Displaystyle \ lim _ {x \ do c} f (x) = f (c).}$

(Przyjęliśmy tutaj, że c jest punktem granicznym dziedziny f .)

Nieruchomości

Jeżeli funkcja f jest rzeczywista, to granica f u p wynosi L , wtedy i tylko wtedy, gdy oba granica praworęcznych i leworęcznych granica f w p istnieją i są równe L .

Funkcja f jest ciągła w p wtedy i tylko wtedy, gdy granica f ( x ) przy x zbliżającym się do p istnieje i jest równa f ( p ). Jeśli f  : M → N jest funkcją między przestrzeniami metrycznymi M i N , to jest to równoważne, że f przekształca każdy ciąg w M zbieżny ku p w ciąg w N zbieżny ku f ( p ).

Jeśli N jest unormowaną przestrzenią wektorów , to operacja graniczna jest liniowa w następującym sensie: jeśli granica f ( x ) w miarę zbliżania się x do p wynosi L , a granica g ( x ) w miarę zbliżania się x do p wynosi P , wówczas granica f ( x ) + g ( x ) gdy x zbliża się do p to L + P . Jeśli a jest skalarem pola bazowego , to granica af ( x ) przy x zbliżającym się do p wynosi aL .

Jeśli f i g są funkcjami o wartościach rzeczywistych (lub zespolonych), to przyjęcie granicy działania na f ( x ) i g ( x ) (np. , , , , ) w pewnych warunkach jest zgodne z działaniem granice f(x) i g(x) . Fakt ten jest często nazywany algebraicznym twierdzeniem granicznym . Głównym warunkiem koniecznym do zastosowania poniższych reguł jest istnienie granic po prawej stronie równań (innymi słowy, granice te są wartościami skończonymi zawierającymi 0). Dodatkowo tożsamość dzielenia wymaga, aby mianownik po prawej stronie był niezerowy (dzielenie przez 0 nie jest zdefiniowane), a tożsamość potęgowania wymaga, aby podstawa była dodatnia lub zero, podczas gdy wykładnik jest dodatni (skończony ). ${\displaystyle f+g}$ ${\displaystyle fg}$ ${\displaystyle f\razy g}$ ${\displaystyle f/g}$ ${\ Displaystyle f ^ {g}}$

${\ Displaystyle {\ zacząć {macierz} \ lim \ limity _ {x \ do p} i (f (x) + g (x)) i = i \ lim \ limity _ {x \ do p} f (x) +\lim \limits _{x\to p}g(x)\\\lim \limits _{x\to p}&(f(x)-g(x))&=&\lim \limits _{ x\to p}f(x)-\lim \limits _{x\to p}g(x)\\\lim \limits _{x\to p}&(f(x)\cdot g(x) )&=&\lim \limits _{x\to p}f(x)\cdot \lim \limits _{x\to p}g(x)\\\lim \limits _{x\to p}& (f(x)/g(x))&=&{\lim \limits _{x\to p}f(x)/\lim \limits _{x\to p}g(x)}\\\ lim \limits _{x\to p}&f(x)^{g(x)}&=&{\lim \limits _{x\to p}f(x)^{\lim \limits _{x\ do p}g(x)}}\end{macierz}}}$

Zasady te obowiązują również dla granic jednostronnych, w tym gdy p wynosi ∞ lub −∞. W każdej powyższej regule, gdy jednym z limitów po prawej stronie jest ∞ lub −∞, limit po lewej stronie może czasami nadal być określony przez następujące reguły.

• q + ∞ = ∞ jeśli q ≠ −∞
• q × ∞ = ∞ jeśli q > 0
• q × ∞ = −∞ jeśli q < 0
• q / ∞ = 0 jeśli q ≠ ∞ i q ≠ −∞
• ∞ ^q = 0 jeśli q < 0
• ∞ ^q = ∞ jeśli q > 0
• q ^∞ = 0 jeśli 0 < q < 1
• q ^∞ = ∞ jeśli q > 1
• q ^−∞ = ∞ jeśli 0 < q < 1
• q ^−∞ = 0 jeśli q > 1

(zobacz także Rozszerzona linia liczb rzeczywistych ).

W innych przypadkach granica po lewej stronie może nadal istnieć, chociaż prawa strona, zwana formą nieokreśloną , nie pozwala na określenie wyniku. Zależy to od funkcji f i g . Te nieokreślone formy to:

• 0 / 0
• ±∞ / ±∞
• 0 × ±∞
• ∞ + −∞
• 0 ⁰
• ∞ ⁰
• 1 ^±∞

Zobacz dalej Reguła L'Hôpital poniżej i Forma nieokreślona .

Granice kompozycji funkcji

Ogólnie rzecz biorąc, od wiedzy o tym

${\ Displaystyle \ lim _ {y \ do b} f (y) = c}$i ,${\ Displaystyle \ lim _ {x \ do} g (x) = b}$

to jednak nie wynika z tego . Jednak ta „reguła łańcucha” obowiązuje, jeśli spełniony jest jeden z następujących dodatkowych warunków: ${\ Displaystyle \ lim _ {x \ do} f (g (x)) = c}$

• f ( b ) = c (czyli f jest ciągłe w b ), lub
• g nie przyjmuje wartości b w pobliżu a (to znaczy istnieje takie, że jeśli to ).${\ Displaystyle \ delta > 0}$${\displaystyle 0<|xa|<\delta}$${\displaystyle |g(x)-b|>0}$

Jako przykład tego zjawiska rozważ następujące funkcje, które naruszają oba dodatkowe ograniczenia:

${\ Displaystyle f (x) = g (x) = {\ zacząć {przypadki} 0 i {\ tekst {jeśli}} x \ neq 0 \ \ 1 i {\ tekst {jeśli}} x = 0 \ koniec {przypadki}} .}$

Ponieważ wartość w f (0) jest usuwalną nieciągłością ,

${\ Displaystyle \ Lim _ {x \ do} f (x) = 0}$dla wszystkich .${\displaystyle a}$

Zatem reguła naiwnego łańcucha sugerowałaby, że granica f ( f ( x )) wynosi 0. Jednak jest tak, że

${\ Displaystyle f (f (x)) = {\ zacząć {przypadki} 1 i {\ tekst {jeśli}} x \ neq 0 \ \ 0 i {\ tekst {jeśli}} x = 0 \ koniec {przypadki}}}$

a więc

${\ Displaystyle \ lim _ {x \ do} f (f (x)) = 1}$dla wszystkich .${\displaystyle a}$

Granice szczególnego zainteresowania

Funkcje wymierne

Dla nieujemnej liczby całkowitej i stałych oraz , ${\ Displaystyle n}$${\displaystyle a_{1},a_{2},a_{3},\ldots,a_{n}}$${\displaystyle b_{1},b_{2},b_{3},\ldots,b_{n}}$

• ${\ Displaystyle \ lim _ {x \ do \ infty} {\ Frac {a_ {1} {x} ^ {n} + a_ {2} {x} ^ {n-1} + a_ {3} {x} ^{n-2}+...+a_{n}}{b_{1}{x}^{n}+b_{2}{x}^{n-1}+b_{3}{x} ^{n-2}+...+b_{n}}}={\frac {a_{1}}{b_{1}}}}$

Można to udowodnić, dzieląc licznik i mianownik przez . Jeśli licznik jest wielomianem wyższego stopnia, granica nie istnieje. Jeśli mianownik ma wyższy stopień, limit wynosi 0. ${\ Displaystyle x ^ {n}}$

Funkcje trygonometryczne

• ${\ Displaystyle \ lim _ {x \ do 0} {\ Frac {\ sin x} {x}} = 1}$
• ${\ Displaystyle \ lim _ {x \ do 0} {\ Frac {1-\ cos x} {x}} = 0}$

Funkcje wykładnicze

• ${\ Displaystyle \ lim _ {x \ do 0} (1 + x) ^ {\ Frac {1} {x}} = \ lim _ {r \ do \ infty} \ lewo (1 + {\ Frac {1} {r}}\prawo)^{r}=e}$
• ${\ Displaystyle \ lim _ {x \ do 0} {\ Frac {e ^ {x} -1} {x}} = 1}$
• ${\ Displaystyle \ lim _ {x \ do 0} {\ Frac {e ^ {ax} -1} {bx}} = {\ Frac {a} {b}}}$
• ${\ Displaystyle \ lim _ {x \ do 0} {\ Frac {c ^ {ax} -1} {bx}} = {\ Frac {a} {b}} \ ln c}$
• ${\ Displaystyle \ lim _ {x \ do 0 ^ {+}} x ^ {x} = 1}$

Funkcje logarytmiczne

• ${\ Displaystyle \ lim _ {x \ do 0} {\ Frac {\ ln (1 + x)} {x}} = 1}$
• ${\ Displaystyle \ lim _ {x \ do 0} {\ Frac {\ ln (1 + ax)} {bx}} = {\ Frac {a} {b}}}$
• ${\ Displaystyle \ lim _ {x \ do 0} {\ Frac {\ log _ {c} (1 + ax)} {bx}} = {\ Frac {a} {b \ ln c}}}$

Zasada L'Hôpital

Ta reguła wykorzystuje pochodne do znalezienia granic nieokreślonych postaci 0/0 lub ±∞/∞ i dotyczy tylko takich przypadków. Do postaci tej można manipulować innymi nieokreślonymi formami. Mając dwie funkcje f ( x ) i g ( x ) określone w otwartym przedziale I zawierającym żądany punkt graniczny c , wtedy jeśli:

1. ${\ Displaystyle \ lim _ {x \ do c} f (x) = \ lim _ {x \ do c} g (x) = 0,}$ lub , i${\ Displaystyle \ lim _ {x \ do c} f (x) = \ pm \ lim _ {x \ do c} g (x) = \ pm \ infty}$
2. ${\displaystyle f}$i są rozróżnialne na , i${\displaystyle g}$${\ Displaystyle I \ setminus \ {c \}}$
3. ${\displaystyle g'(x)\neq 0}$dla wszystkich i${\ Displaystyle x \ w I \ setminus \ {c \}}$
4. ${\ Displaystyle \ lim _ {x \ do c} {\ Frac {f '(x)} {g' (x)}}}$ istnieje,

następnie:

${\ Displaystyle \ lim _ {x \ do c} {\ Frac {f (x)} {g (x)}} = \ lim _ {x \ do c} {\ Frac {f '(x)} {g '(x)}}}$

Zwykle najważniejszy jest pierwszy warunek.

Na przykład: ${\ Displaystyle \ lim _ {x \ do 0} {\ Frac {\ grzech (2x)} {\ grzech (3x)}} = \ lim _ {x \ do 0} {\ Frac {2 \ cos (2x) }{3\cos(3x)}}={\frac {2\cdot 1}{3\cdot 1}}={\frac {2}{3}}.}$

Sumowania i całki

Określanie nieskończonego ograniczenia sumy lub całki jest powszechnym skrótem określania limitu.

Krótkim sposobem na zapisanie limitu jest . Ważnym przykładem limitów takich sum są szeregi . ${\ Displaystyle \ lim _ {n \ do \ infty} \ suma _ {i = s} ^ {n} f (i)}$${\ Displaystyle \ suma _ {i = s} ^ {\ infty} f (i)}$

Krótkim sposobem na zapisanie limitu jest . ${\ Displaystyle \ lim _ {x \ do \ infty} \ int _ {a} ^ {x} f (t) \; dt}$${\ Displaystyle \ int _ {a} ^ {\ infty} f (t) \; dt}$

Krótkim sposobem na zapisanie limitu jest . ${\ Displaystyle \ lim _ {x \ do - \ infty} \ int _ {x} ^ {b} f (t) \; dt}$${\ Displaystyle \ int _ {- \ infty} ^ {b} f (t) \; dt}$

Zobacz też

• Notacja Big O  – Notacja opisująca ograniczające zachowanie
• Reguła L'Hôpitala  – matematyczna reguła oceny pewnych granic
• Lista limitów  – artykuł z listy Wikipedii
• Granica sekwencji  — wartość, do której „skłaniają się” terminy sekwencji
• Limit wyższy i limit niższy
• Net (matematyka)  – uogólnienie ciągu punktów
• Rachunek niestandardowy
• Twierdzenie o ściśnięciu  – o obliczaniu granic przez ograniczenie funkcji między dwiema innymi funkcjami
• Granica sekwencyjna  – Granica pewnego podciągu

Uwagi

Bibliografia

• Apostol, Tom M. (1974), Analiza matematyczna (2 wyd.), Addison-Wesley, ISBN 0-201-00288-4
• Bartle, Robert (1967), Elementy analizy rzeczywistej , Wiley
• Courant, Richard (1924), Vorlesungen über Differential- und Integralrechnung , Springer Verlag
• Hardy, GH (1921), Kurs czystej matematyki , Cambridge University Press
• Hubbard, John H. (2015), Rachunek wektorowy, algebra liniowa i formy różniczkowe: ujednolicone podejście (wyd. piąte), edycje macierzy
• Strona, Warren; Hersz, Ruben; Seldena, Annie; et al., wyd. (2002), "Najważniejsze media", The College Mathematics , 33 (2): 147-154, JSTOR  2687124.
• Rudin, Walter (1964), Zasady analizy matematycznej , McGraw-Hill
• Sutherland, WA (1975), Wprowadzenie do przestrzeni metrycznych i topologicznych , Oxford: Oxford University Press, ISBN 0-19-853161-3
• Sherbert, Robert (2000), Wprowadzenie do analizy rzeczywistej , Wiley
• Whittakera ; Watson (1904), Kurs współczesnej analizy , Cambridge University Press

Zewnętrzne linki

• MacTutor Historia Weierstrassa.
• MacTutor Historia Bolzano
• Rachunek wizualny przez Lawrence S. Husch , University of Tennessee (2001)