Sekwencja o małej rozbieżności - Low-discrepancy sequence

W matematyce ciąg o małej rozbieżności jest ciągiem o własności, że dla wszystkich wartości N , jego podciąg x ₁ , ..., x _N ma małą rozbieżność .

Z grubsza rzecz biorąc, rozbieżność sekwencji jest niska, jeśli proporcja punktów w sekwencji należących do dowolnego zbioru B jest blisko proporcjonalna do środka z B , jak stałoby się przeciętnie (ale nie dla poszczególnych próbek) w przypadku equidistributed sekwencji . Konkretne definicje rozbieżności różnią się w odniesieniu do wyboru B ( hipersfery , hipersześciany itp.) oraz sposobu obliczania rozbieżności dla każdego B (zwykle znormalizowanego) i łączenia (zwykle poprzez przyjęcie najgorszej wartości).

Ciągi o małej rozbieżności nazywane są również ciągami quasilosowymi , ze względu na ich powszechne zastosowanie jako zamiennik liczb losowych o rozkładzie jednostajnym . Modyfikator „quasi” służy do wyraźniejszego zaznaczenia, że ​​wartości ciągu o małej rozbieżności nie są ani losowe, ani pseudolosowe , ale takie ciągi mają pewne właściwości zmiennych losowych i w niektórych zastosowaniach, takich jak metoda quasi-Monte Carlo, mają mniejszą rozbieżność to ważna zaleta.

Aplikacje

Błąd w szacowanej kurtozie jako funkcja liczby punktów danych. 'Dodatkowe quasilosowe' daje maksymalny błąd, gdy c  = ( √ 5  − 1)/2. „Losowe” daje średni błąd w sześciu ciągach liczb losowych, gdzie średnia jest brana pod uwagę w celu zmniejszenia wielkości dzikich fluktuacji

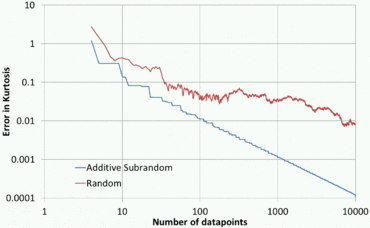
Liczby quasilosowe mają przewagę nad czystymi liczbami losowymi, ponieważ szybko i równomiernie pokrywają interesującą dziedzinę. Mają przewagę nad czysto deterministycznymi metodami, ponieważ metody deterministyczne zapewniają wysoką dokładność tylko wtedy, gdy liczba punktów danych jest wstępnie ustawiona, podczas gdy przy użyciu sekwencji quasi-losowych dokładność zwykle poprawia się w sposób ciągły, gdy dodawanych jest więcej punktów danych, z pełnym ponownym wykorzystaniem istniejących punktów. Z drugiej strony zbiory punktów quasi-losowych mogą mieć znacznie mniejszą rozbieżność dla danej liczby punktów niż ciągi czysto losowe.

Przydatnym zastosowania to znalezienia funkcji charakterystycznej o funkcji gęstości prawdopodobieństwa , i znalezienie pochodnej funkcji deterministycznej funkcji z niewielką ilością szumów. Liczby quasilosowe umożliwiają bardzo szybkie obliczenie momentów wyższego rzędu z dużą dokładnością.

Zastosowania, które nie wymagają sortowania, to znajdowanie średniej , odchylenia standardowego , skośności i kurtozy rozkładu statystycznego oraz znajdowanie całkowitych i globalnych maksimów i minimów trudnych funkcji deterministycznych. Liczby quasilosowe mogą być również używane do dostarczania punktów początkowych dla algorytmów deterministycznych, które działają tylko lokalnie, takich jak iteracja Newtona-Raphsona .

Liczby quasilosowe można również łączyć z algorytmami wyszukiwania. Algorytm w stylu Quicksort drzewa binarnego powinien działać wyjątkowo dobrze, ponieważ liczby quasilosowe spłaszczają drzewo znacznie lepiej niż liczby losowe, a im bardziej płaskie drzewo, tym szybsze sortowanie. Z algorytmu wyszukiwania, numery quasirandom mogą być wykorzystywane w celu znalezienia tryb , mediana , przedziały ufności i skumulowany rozkład z rozkładem statystycznym, a wszystkie lokalne minima i wszystkie rozwiązania funkcji deterministycznych.

Ciągi o małej rozbieżności w całkowaniu numerycznym

Co najmniej trzy metody całkowania numerycznego można sformułować w następujący sposób. Mając zbiór { x ₁ , ..., x _N } w przedziale [0,1], aproksymuj całkę funkcji f jako średnią z funkcji obliczonej w tych punktach:

${\ Displaystyle \ int _ {0} ^ {1} f (u) \ du \ około {\ Frac {1} {N}} \ \ suma _ {i = 1} ^ {N} f (x_ { ja}).}$

Jeśli punkty są wybrane jako x _i = i / N , jest to reguła prostokąta . Jeśli punkty są wybierane do losowego (lub pseudolosowego ) rozdzielenia, jest to metoda Monte Carlo . Jeżeli punkty są wybrane jako elementy ciągu o małej rozbieżności, jest to metoda quasi-Monte Carlo . Godny uwagi wynik, nierówność Koksmy-Hlawki (podana poniżej), pokazuje, że błąd takiej metody może być ograniczony iloczynem dwóch wyrazów, z których jeden zależy tylko od f , a drugi to rozbieżność zbioru { x ₁ , ..., x _N }.

Jest wygodne, aby skonstruować zestaw { x ₁ , ..., x _N }, w taki sposób, że jeśli zbiór z N +1 elementów jest zbudowana, poprzednie N elementy nie muszą być ponownie obliczonych. Reguła prostokąta wykorzystuje zestaw punktów, które mają małą rozbieżność, ale ogólnie elementy muszą być przeliczone, jeśli N jest zwiększone. Elementy nie muszą być przeliczane w losowej metodzie Monte Carlo, jeśli N jest zwiększone, ale zbiory punktów nie mają minimalnej rozbieżności. Używając sekwencji o małej rozbieżności, dążymy do małej rozbieżności i nie ma potrzeby ponownego obliczania, ale w rzeczywistości sekwencje o małej rozbieżności mogą być przyrostowo dobre tylko w przypadku rozbieżności, jeśli nie pozwolimy na ponowne przeliczenie.

Definicja rozbieżności

Rozbieżność o zadanej P = { x ₁ , ..., x _N } zdefiniowano za pomocą Niederreiter w notacji jako

${\ Displaystyle D_ {N} (P) = \ sup _ {B \ w J} \ lewo | {\ Frac {A (B; P)} {N}} - \ lambda _ {s} (B) \ po prawej |}$

gdzie λ _s jest s- wymiarową miarą Lebesgue'a , A ( B ; P ) jest liczbą punktów w P , które wpadają w B , a J jest zbiorem s- wymiarowych przedziałów lub pudełek postaci

${\ Displaystyle \ prod _ {i = 1} ^ {s} [a_ {i}, b_ {i}) = \ {\ mathbf {x} \ w \ mathbf {R} ^ {s}: a_ {i} \leq x_{i}<b_{i}\}\,}$

gdzie . ${\ Displaystyle 0 \ równoważnik a_ {i} <b_ {i} \ równoważnik 1}$

Gwiazdy rozbieżność D ^* _N ( P ) jest określony w podobny sposób, z tym że Supremum przejmuje zestaw J ^* pudeł prostokątnych formie

${\ Displaystyle \ prod _ {i = 1} ^ {s} [0, u_ {i})}$

gdzie u _i jest w przedziale półotwartym [0, 1).

Oba są powiązane przez

${\ Displaystyle D_ {N} ^ {*} \ równoważnik D_ {N} \ równoważnik 2 ^ {s} D_ {N} ^ {*}. \,}$

Uwaga: W przypadku tych definicji rozbieżność reprezentuje najgorszy przypadek lub maksymalne odchylenie gęstości punktów jednolitego zestawu. Istotne są jednak również inne miary błędów, co prowadzi do innych definicji i miar zmienności. Na przykład, rozbieżność L2 lub zmodyfikowana wyśrodkowana rozbieżność L2 są również intensywnie wykorzystywane do porównywania jakości jednolitych zbiorów punktów. Oba są znacznie łatwiejsze do obliczenia dla dużych N i s.

Nierówność Koksmy–Hławki

Niech Ī ^s będzie s- wymiarowym sześcianem jednostkowym, Ī ^s = [0, 1] × ... × [0, 1]. Niech f ma ograniczoną wariację V ( f ) na Ī ^s w sensie Hardy'ego i Krausego. Wtedy dla dowolnego x ₁ , ..., x _N w I ^s = [0, 1) × ... × [0, 1),

${\ Displaystyle \ lewo | {\ Frac {1} {N}} \ suma _ {i = 1} ^ {N} f (x_ {i}) - \ int _ {{\ bar {I}} ^ {s }}f(u)\,du\right|\leq V(f)\,D_{N}^{*}(x_{1},\ldots ,x_{N}).}$

Koksma - Hlawka nierówność jest ostry w następującym sensie: Dla każdego zestawu punktów { x ₁ , ..., x _N } w I ^a i każda znajduje się funkcja f o ograniczonej zmienności i V, ( f ) = 1, tak że ${\ Displaystyle \ varepsilon > 0}$

${\ Displaystyle \ lewo | {\ Frac {1} {N}} \ suma _ {i = 1} ^ {N} f (x_ {i}) - \ int _ {{\ bar {I}} ^ {s }}f(u)\,du\right|>D_{N}^{*}(x_{1},\ldots ,x_{N})-\varepsilon .}$

Dlatego jakość liczbowej reguły całkowania zależy tylko od rozbieżności D ^* _N ( x ₁ ,..., x _N ).

Formuła Hławki-Zaremby

Niech . Bo piszemy ${\displaystyle D=\{1,2,\ldots,d\}}$${\ Displaystyle \ pusty zestaw \ neq u \ podseteq D}$

${\ Displaystyle dx_ {u}: = \ prod _ {j \ w u} dx_ {j}}$

i oznaczać przez punkt otrzymany z x przez zastąpienie współrzędnych nie w u przez . Następnie ${\ Displaystyle (x_ {u}, 1)}$${\ Displaystyle 1}$

${\ Displaystyle {\ Frac {1} {N}} \ suma _ {i = 1} ^ {N} f (x_ {i}) - \ int _ {{\ bar {I}} ^ {s}} f (u)\,du=\sum _{\emptyset \neq u\subseteq D}(-1)^{|u|}\int _{[0,1]^{|u|}}\operatorname {dysk } (x_{u},1){\frac {\częściowy ^{|u|}}{\częściowy x_{u}}}f(x_{u},1)\,dx_{u},}$

gdzie jest funkcja rozbieżności. ${\ Displaystyle \ Operatorname {dysk} (z) = {\ Frac {1} {N}} \ suma _ {i = 1} ^ {N} \ prod _ {j = 1} ^ {d} 1_ {[0 ,z_{j})}(x_{i,j})-\prod _{j=1}^{d}z_{i}}$

Wersja nierówności Koksma-Hlawka${\ Displaystyle L ^ {2}}$

Stosując nierówność Cauchy'ego-Schwarza dla całek i sum do tożsamości Hławki-Zaremby otrzymujemy wersję nierówności Koksmy-Hlawki: ${\ Displaystyle L ^ {2}}$

${\ Displaystyle \ lewo | {\ Frac {1} {N}} \ suma _ {i = 1} ^ {N} f (x_ {i}) - \ int _ {{\ bar {I}} ^ {s }}f(u)\,du\right|\leq \|f\|_{d}\nazwa operatora {dysk} _{d}(\{t_{i}\}),}$

gdzie

${\ Displaystyle \ operatorname {dysk} _ {d} (\ {t_ {i} \}) = \ lewo (\ suma _ {\ pusty zestaw \ neq u \ podseteq D} \ int _ {[0,1] ^ { |u|}}\nazwa operatora {dysk} (x_{u},1)^{2}\,dx_{u}\right)^{1/2}}$

i

${\ Displaystyle \ | f \ | _ {d} = \ lewo (\ suma _ {u \ podseteq D} \ int _ {[0,1] ^ {| u |}} \ lewo | {\ Frac {\ częściowy ^{|u|}}{\częściowy x_{u}}}f(x_{u},1)\right|^{2}dx_{u}\right)^{1/2}.}$

Rozbieżność L2 ma duże znaczenie praktyczne, ponieważ dla danego zbioru punktów możliwe są szybkie obliczenia jawne. W ten sposób łatwo jest tworzyć optymalizatory zestawu punktów, używając jako kryterium rozbieżności L2.

Nierówność Erdősa–Turana–Koksmy

Obliczeniowo trudno jest znaleźć dokładną wartość rozbieżności dużych zbiorów punktów. Erdős - Turan - Koksma nierówność stanowi górną granicę.

Niech x ₁ ,..., x _N będą punktami w I ^s a H będzie dowolną dodatnią liczbą całkowitą. Następnie

${\ Displaystyle D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) \ leq \ lewo ({\ Frac {3} {2}} \ po prawej) ^ {s} \ po lewej ( {\frac {2}{H+1}}+\sum _{0<\|h\|_{\infty }\leq H}{\frac {1}{r(h)}}\left|{ \frac {1}{N}}\sum _{n=1}^{N}e^{2\pi i\langle h,x_{n}\rangle }\right|\right)}$

gdzie

${\ Displaystyle r (h) = \ prod _ {i = 1} ^ {s} \ max \ {1, | h_ {i} | \} \ quad {\ mbox {dla}} \ quad h = (h_ { 1},\ldots ,h_{s})\in \mathbb {Z} ^{s}.}$

Główne przypuszczenia

Hipoteza 1. Istnieje stała c _s zależna tylko od wymiaru s , taka, że

${\ Displaystyle D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) \ geq c_ {s} {\ Frac {(\ ln N) ^ {s-1}} {N} }}$

dla dowolnego zbioru punktów skończonych { x ₁ ,..., x _N }.

Hipoteza 2. Istnieje stała c ^' _s zależna tylko od s , taka, że

${\ Displaystyle D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) \ geq c '_ {s} {\ Frac {(\ ln N) ^ {s}} {N} }}$

dla nieskończonej liczby N dla dowolnej nieskończonej sekwencji x ₁ , x ₂ , x ₃ ,....

Te przypuszczenia są równoważne. Zostały one udowodnione dla s ≤ 2 przez WM Schmidta . W wyższych wymiarach odpowiedni problem jest wciąż otwarty. Najbardziej znane dolne granice należą do Michaela Laceya i współpracowników.

Dolne granice

Niech s  = 1. Wtedy

${\ Displaystyle D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) \ geq {\ Frac {1} {2N}}}$

dla dowolnego zbioru punktów skończonych { x ₁ , ...,  x _N }.

Niech s  = 2. WM Schmidt udowodnił, że dla dowolnego zbioru punktów skończonych { x ₁ , ...,  x _N },

${\ Displaystyle D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) \ geq C {\ Frac {\ log N} {N}}}$

gdzie

${\ Displaystyle C = \ max _ {a \ geq 3} {\ Frac {1} {16}} {\ Frac {a-2} {a \ log a}} = 0,023335 \ kropki.}$

Dla dowolnych wymiarów s  > 1 KF Roth udowodnił, że

${\ Displaystyle D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) \ geq {\ Frac {1} {2 ^ {4 s}}} {\ Frac {1} {(((() s-1)\log 2)^{\frac {s-1}{2}}}}{\frac {\log ^{\frac {s-1}{2}}N}{N}}}$

dla dowolnego zbioru punktów skończonych { x ₁ , ...,  x _N }. Józef Beck ustalił dwukrotną poprawę tego wyniku w trzech wymiarach. Zostało to ulepszone przez D. Bilyka i MT Lacey do potęgi pojedynczego logarytmu. Najbardziej znanym wiązaniem dla s  > 2 są D. Bilyk i MT Lacey oraz A. Vagharshakyan. Dla s  > 2 istnieje t  > 0, więc

${\ Displaystyle D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) \ geq t {\ Frac {\ log ^ {{\ Frac {s-1} {2}} + t }N}{N}}}$

dla dowolnego zbioru punktów skończonych { x ₁ , ...,  x _N }.

Konstruowanie ciągów o małej rozbieżności

Ponieważ dowolny rozkład liczb losowych może być odwzorowany na rozkład jednostajny, a liczby quasi-losowe są odwzorowane w ten sam sposób, ten artykuł dotyczy tylko generowania liczb quasi-losowych na wielowymiarowym rozkładzie jednostajnym.

Znane są konstrukcje sekwencji, takie, że

${\ Displaystyle D_ {N} ^ {*} (x_ {1}, \ ldots, x_ {N}) \ Leq C {\ Frac {(\ ln N) ^ {s}} {N}}.}$

gdzie C jest pewną stałą, w zależności od sekwencji. Po hipotezie 2 uważa się, że sekwencje te mają najlepszą możliwą kolejność zbieżności. Poniższe przykłady są van der sekwencji Corput , w sekwencji Halton , oraz sekwencji Sobol . Jednym z ogólnych ograniczeń jest to, że metody konstrukcyjne mogą zwykle gwarantować tylko porządek zbieżności. Praktycznie małą rozbieżność można osiągnąć tylko wtedy, gdy N jest wystarczająco duże, a dla dużych danych s to minimalne N może być bardzo duże. Oznacza to, że przeprowadzenie analizy Monte-Carlo z np. s=20 zmiennymi i N=1000 punktów z generatora sekwencji o małej rozbieżności może zapewnić tylko bardzo niewielką poprawę dokładności.

Losowe liczby

Sekwencje liczb quasilosowych można generować z liczb losowych, nakładając ujemną korelację na te liczby losowe. Jednym ze sposobów, aby to zrobić, aby rozpocząć z zestawem liczb losowych na i cyfr konstrukt quasirandom które są jednorodne na podstawie: ${\displaystyle r_{i}}$${\ Displaystyle [0,0.5)}$${\displaystyle s_{i}}$${\ Displaystyle [0,1)}$

${\displaystyle s_{i}=r_{i}}$dla nieparzystych i do wieczora. ${\displaystyle i}$${\ Displaystyle s_ {i} = 0,5 + r_ {i}}$${\displaystyle i}$

Drugim sposobem na zrobienie tego z początkowymi liczbami losowymi jest skonstruowanie błądzenia losowego z przesunięciem 0.5, jak w:

${\ Displaystyle s_ {i} = s_ {i-1} + 0,5 + r_ {i} {\ pmod {1}}. \,}$

Oznacza to, że weź poprzednią liczbę quasilosową, dodaj 0,5 i liczbę losową i weź wynik modulo  1.

W przypadku więcej niż jednego wymiaru można użyć kwadratów łacińskich o odpowiednim wymiarze, aby zapewnić przesunięcia, aby zapewnić równomierne pokrycie całej domeny.

Pokrycie kwadratu jednostkowego. Po lewej dla addytywnych liczb quasi-losowych z c  = 0.5545497..., 0.308517... Po prawej dla liczb losowych. Od góry do dołu. 10, 100, 1000, 10000 punktów.

Nawrót addytywny

Dla każdego irracjonalnego sekwencja ${\ Displaystyle \ alfa}$

${\ Displaystyle s_ {n} = \ {s_ {0}+ n \ alfa \}}$

ma rozbieżności zmierzające do . Zauważ, że sekwencja może być zdefiniowana rekurencyjnie przez ${\ Displaystyle 1/N}$

${\ Displaystyle s_ {n + 1} = (s_ {n} + \ alfa) {\ bmod {\,}} 1 \;.}$

Dobra wartość daje mniejszą rozbieżność niż ciąg niezależnych jednolitych liczb losowych. ${\ Displaystyle \ alfa}$

Rozbieżność może być ograniczony przez wykładnik aproksymacji z . Jeśli wykładnikiem aproksymacji jest , to dla any , obowiązuje następujące ograniczenie: ${\ Displaystyle \ alfa}$${\ Displaystyle \ mu}$${\ Displaystyle \ varepsilon > 0}$

${\ Displaystyle D_ {N} ((s_ {n})) = O_ {\ varepsilon} (N ^ {-1/(\ mu -1) + \ varepsilon}).}$

Według twierdzenia Thue-Siegla-Rotha wykładnik aproksymacji dowolnej niewymiernej liczby algebraicznej wynosi 2, co daje granicę powyżej. ${\ Displaystyle N ^ {-1+ \ varepsilon}}$

Powyższa relacja rekurencyjna jest podobna do relacji rekurencyjnej używanej przez liniowy generator kongruencji , niskiej jakości generator liczb pseudolosowych:

${\ Displaystyle R_ {i} = (ar_ {i-1} + c) {\ bmod {m}}}$

Dla powyższej, addytywnej powtarzalności o niskiej rozbieżności, aim są wybierane jako 1. Należy jednak pamiętać, że nie spowoduje to wygenerowania niezależnych liczb losowych, więc nie powinno być używane do celów wymagających niezależności.

Wartość z najmniejszą rozbieżnością to ${\displaystyle c}$

${\ Displaystyle c = {\ Frac {{\ sqrt {5}}-1} {2}} \ około 0,618034.}$

Inną wartością, która jest prawie tak dobra, jest:

${\ Displaystyle c = {\ sqrt {2}} -1 \ około 0,414214. \,}$

W więcej niż jednym wymiarze dla każdego wymiaru potrzebne są oddzielne liczby quasi-losowe. Wygodny zestaw wartości, które są używane, to pierwiastki kwadratowe liczb pierwszych od dwóch w górę, wszystkie wzięte modulo 1:

${\ Displaystyle c = {\ sqrt {2}}, {\ sqrt {3}}, {\ sqrt {5}}, {\ sqrt {7}}, {\ sqrt {11}}, \ ldots \,}$

Wykazano jednak, że zestaw wartości opartych na uogólnionym złotym podziale daje bardziej równomiernie rozłożone punkty.

Lista generator liczb pseudolosowych metod list do generowania liczb pseudolosowych niezależnych. Uwaga: W kilku wymiarach rekurencyjna rekurencja prowadzi do jednolitych zbiorów dobrej jakości, ale dla większych s (takich jak s>8) inne generatory zbiorów punktów mogą oferować znacznie mniejsze rozbieżności.

Sekwencja van der Corputa

Pozwolić

${\ Displaystyle n = \ suma _ {k = 0} ^ {L-1} d_ {k} (n) b ^ {k}}$

będzie b- arną reprezentacją dodatniej liczby całkowitej n ≥ 1, tj. 0 ≤ d _k ( n ) < b . Zestaw

${\ Displaystyle g_ {b} (n) = \ suma _ {k = 0} ^ {L-1} d_ {k} (n) b ^ {-k-1}.}$

Wtedy istnieje stała C zależna tylko od b taka, że ​​( g _b ( n )) _{n ≥ 1} spełnia

${\ Displaystyle D_ {N} ^ {*} (g_ {b} (1), \ kropki, g_ {b} (N)) \ leq C {\ Frac {\ log N} {N}}}$

gdzie D ^* _N jest rozbieżnością gwiazdy .

Sekwencja Haltona

Pierwsze 256 punktów ciągu (2,3) Haltona

Sekwencja Haltona jest naturalnym uogólnieniem sekwencji van der Corputa do wyższych wymiarów. Niech s będzie dowolnym wymiarem, a b ₁ , ..., b _s będą dowolnymi względnie pierwszymi liczbami całkowitymi większymi niż 1. Zdefiniuj

${\ Displaystyle x (n) = (g_ {b_ {1}} (n), \ kropki, g_ {b_ {s}} (n)).}$

Wtedy istnieje stała C zależna tylko od b ₁ , ..., b _s , taka że ciąg { x ( n )} _{n ≥1} jest ciągiem s- wymiarowym z

${\ Displaystyle D_ {N} ^ {*} (x (1), \ kropki, x (N)) \ leq C '{\ Frac {(\ log N) ^ {s}} {N}}.}$

Zestaw Hammersley

Zestaw 2D Hammersley w rozmiarze 256

Niech b ₁ , ..., b _{s -1} być względnie pierwsze dodatnie liczby całkowite większe od 1. Na podane s i N The s wymiarową Hammersley zestaw rozmiarów N jest określona przez

${\ Displaystyle x (n) = (g_ {b_ {1}} (n), \ kropki, g_ {b_ {s-1}} (n), {\ Frac {n} {N}})}$

dla n = 1, ..., N . Następnie

${\ Displaystyle D_ {N} ^ {*} (x (1), \ kropki, x (N)) \ Leq C {\ Frac {(\ log N) ^ {s-1}} {N}}}$

gdzie C jest stałą zależną tylko od b ₁ , ..., b _{s -1} . Uwaga: Wzory pokazują, że zbiór Hammersleya jest w rzeczywistości sekwencją Haltona, ale otrzymujemy jeszcze jeden wymiar za darmo, dodając przeciągnięcie liniowe. Jest to możliwe tylko wtedy, gdy N jest znane z góry. Zbiór liniowy jest również ogólnie zbiorem o najmniejszej możliwej rozbieżności jednowymiarowej. Niestety, dla wyższych wymiarów nie są znane takie „zestawy rekordów rozbieżności”. Dla s  = 2, większość generatorów zestawu punktów o małej rozbieżności dostarcza co najmniej rozbieżności bliskie optymalnej.

Sekwencja Sobola

Wariant Antonowa-Saleeva sekwencji Sobola generuje liczby od zera do jedynki bezpośrednio jako binarne ułamki długości , ze zbioru specjalnych ułamków binarnych, zwanych liczbami kierunkowymi. Bity kodu Grey z , , służą do wybierania numerów kierunkowych. Aby uzyskać wartość sekwencji Sobola, weź wyłączną lub binarną wartość kodu Graya z odpowiednim numerem kierunkowym. Liczba wymaganych wymiarów wpływa na wybór . ${\ Displaystyle w}$${\ Displaystyle w}$${\ Displaystyle V_ {i}, i = 1,2, \ kropki, w}$${\displaystyle i}$${\ Displaystyle G (i)}$${\displaystyle s_{i}}$${\displaystyle i}$${\ Displaystyle V_ {i}}$

Próbkowanie dysku Poissona

Próbkowanie dysku Poissona jest popularne w grach wideo do szybkiego umieszczania obiektów w sposób, który wydaje się losowo wyglądać, ale gwarantuje, że co dwa punkty są oddzielone co najmniej określoną minimalną odległością. Nie gwarantuje to małej rozbieżności (jak np. Sobol), ale przynajmniej znacznie mniejszej rozbieżności niż czysto losowe próbkowanie. Cel tych wzorców próbkowania opiera się na analizie częstotliwości, a nie na rozbieżności, rodzaju tak zwanych wzorców „niebieskiego szumu”.

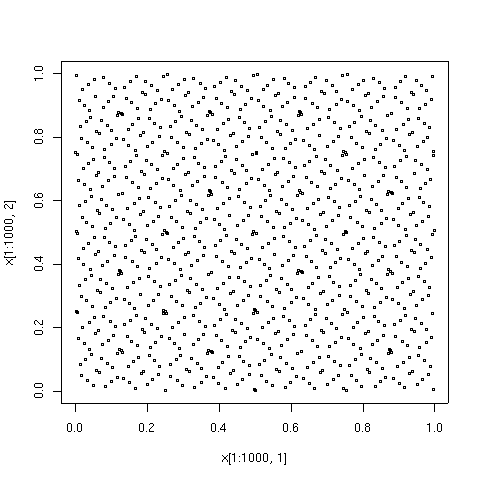
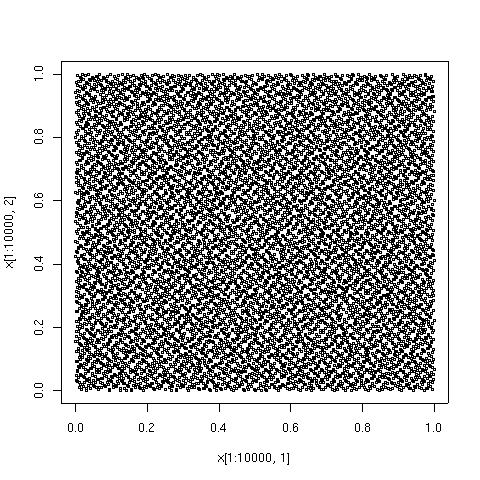
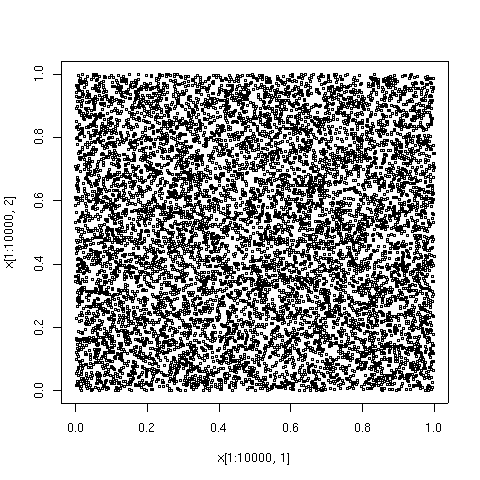
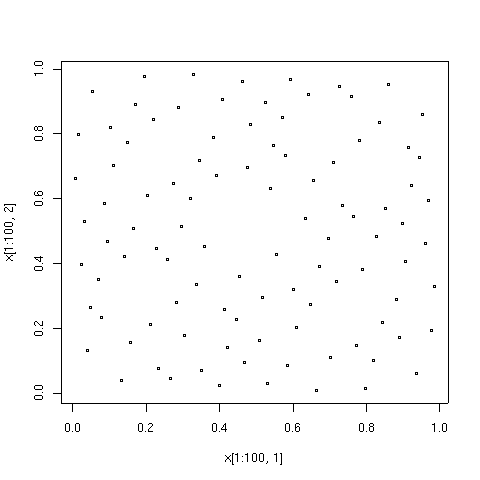
Przykłady graficzne

Punkty narysowane poniżej to pierwsze 100, 1000 i 10000 elementów w sekwencji typu Sobola. Dla porównania pokazano również 10000 elementów ciągu punktów pseudolosowych. Sekwencja o małej rozbieżności została wygenerowana przez algorytm TOMS 659. Implementacja algorytmu w Fortran jest dostępna z Netlib .

Pierwsze 100 punktów w sekwencji o małej rozbieżności typu Sobol .

Pierwsze 1000 punktów w tej samej kolejności. Te 1000 to pierwsze 100, z 900 dodatkowymi punktami.

Pierwsze 10000 punktów w tej samej kolejności. Te 10000 stanowią pierwsze 1000, z 9000 więcej punktów.

Dla porównania, oto pierwsze 10000 punktów w ciągu równomiernie rozłożonych liczb pseudolosowych. Widoczne są regiony o większej i mniejszej gęstości.

Zobacz też

• Teoria rozbieżności
• Łańcuch Markowa Monte Carlo
• Metoda Quasi-Monte Carlo
• Rzadka siatka

Uwagi

Bibliografia

• Josef Dick i Friedrich Pillichshammer, Sieci i sekwencje cyfrowe. Teoria rozbieżności i integracja Quasi-Monte Carlo , Cambridge University Press, Cambridge, 2010, ISBN  978-0-521-19159-3
• Kuipers, L.; Niederreiter, H. (2005), Jednolity rozkład sekwencji , Dover Publications , ISBN 0-486-45019-8
• Haralda Niederreitera . Generowanie liczb losowych i metody quasi-Monte Carlo. Towarzystwo Matematyki Przemysłowej i Stosowanej, 1992. ISBN  0-89871-295-5
• Michael Drmota i Robert F. Tichy, Sekwencje, rozbieżności i zastosowania , Lecture Notes in Math., 1651, Springer, Berlin, 1997, ISBN  3-540-62606-9
• William H. Press, Brian P. Flannery, Saul A. Teukolsky, William T. Vetterling. Przepisy numeryczne w C . Cambridge, Wielka Brytania: Cambridge University Press, wydanie drugie 1992. ISBN  0-521-43108-5 (patrz rozdział 7.7 dla mniej technicznej dyskusji o sekwencjach o małej rozbieżności)

Linki zewnętrzne

• Zebrane algorytmy ACM (patrz algorytmy 647, 659 i 738.)
• Sekwencje quasi-losowe z Biblioteki Naukowej GNU
• Próbkowanie quasi-losowe z zastrzeżeniem ograniczeń w FinancialMathematics.Com
• Generator C++ sekwencji Sobola