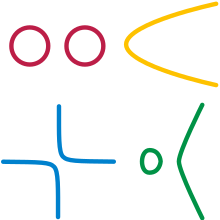Kolektor - Manifold


W matematyce , o kolektorze jest przestrzenią topologiczną , że lokalnie przypomina przestrzeni euklidesowej pobliżu każdego punktu. Dokładniej An n wymiarową kolektora lub n -manifold w skrócie, jest przestrzenią topologiczną z własności, że każdy punkt ma okolicy , która jest homeomorficzny do otwartego podzbioru n -wymiarowej przestrzeni euklidesowej.
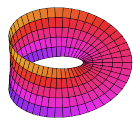
Rozmaitości jednowymiarowe obejmują linie i okręgi , ale nie ósemki . Rozmaitości dwuwymiarowe nazywane są również powierzchniami . Przykłady obejmują płaszczyznę , kulę i torus , a także butelkę Kleina i prawdziwą płaszczyznę rzutową .
Pojęcie rozmaitości ma kluczowe znaczenie dla wielu części geometrii i współczesnej fizyki matematycznej, ponieważ umożliwia opisywanie skomplikowanych struktur w kategoriach dobrze rozumianych właściwości topologicznych prostszych przestrzeni. Rozmaitości powstają naturalnie jako zbiory rozwiązań układów równań i jako wykresy funkcji. Koncepcja ma zastosowanie w grafice komputerowej i rozszerzonej rzeczywistości ze względu na konieczność powiązania obrazów ze współrzędnymi (np. skany CT).
Rozdzielacze mogą być wyposażone w dodatkową konstrukcję. Jedną z ważnych klas rozmaitości są rozmaitości różniczkowe ; ich różniczkowa struktura umożliwia wykonanie rachunku różniczkowego . Riemanna metrycznych na kolektorze umożliwia odległości i kąty mierzone. Kolektory symplektyczne służyć jako przestrzeń fazowa w Hamiltona formalizmu w mechanice , a czterowymiarowy lorentzowskiej kolektory modelu czasoprzestrzeni w ogólnym wzgl .
Badanie rozmaitości wymaga praktycznej znajomości rachunku różniczkowego i topologii .
Motywujące przykłady
Koło
Po prostej okrąg jest najprostszym przykładem rozmaitości topologicznej. Topologia ignoruje zginanie, więc mały fragment okręgu jest traktowany tak samo jak mały fragment linii. Rozważmy na przykład górną część okręgu jednostkowego , x 2 + y 2 = 1 , gdzie współrzędna y jest dodatnia (oznaczona żółtym łukiem na rysunku 1 ). Każdy punkt tego łuku może być jednoznacznie opisany przez jego współrzędną x . Tak więc, występ na pierwszym współrzędnych jest ciągły i odwracalna , mapowanie z górnego łuku do otwartego przedziału (1, 1):
Takie funkcje wraz z mapowanymi przez nie obszarami otwartymi nazywane są wykresami . Podobnie istnieją wykresy dla dolnej (czerwonej), lewej (niebieskiej) i prawej (zielonej) części koła:
Razem te części pokrywają cały krąg, a cztery wykresy tworzą atlas koła.
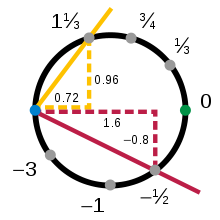
Górny i prawy wykresy, i odpowiednio pokrywają się w ich domenie: ich kłamstwa skrzyżowanie w ćwierci okręgu gdzie zarówno i -coordinates są pozytywne. Każdy odwzorowuje tę część na przedział , choć inaczej. W ten sposób można skonstruować funkcję , która pobiera wartości ze współdziedziny z powrotem do okręgu za pomocą odwrotności, a następnie z powrotem do przedziału. Dla dowolnej liczby a w , wtedy:
Taka funkcja nazywana jest mapą przejścia .
Wykresy górny, dolny, lewy i prawy nie tworzą jedynego możliwego atlasu. Wykresy nie muszą być rzutami geometrycznymi, a liczba wykresów jest kwestią wyboru. Rozważ wykresy
Tutaj s jest nachyleniem linii przechodzącej przez punkt o współrzędnych ( x , y ) i ustalonym punkcie obrotu (-1, 0); podobnie, t jest przeciwieństwem nachylenia linii przechodzącej przez punkty o współrzędnych ( x , y ) i (+1, 0). Odwrotne odwzorowanie z s na ( x , y ) jest podane przez
Można potwierdzić, że x 2 + y 2 = 1 dla wszystkich wartości s i t . Te dwa wykresy stanowią drugi atlas koła z mapą przejścia
Każdy wykres pomija pojedynczy punkt, albo (-1, 0) dla s albo (+1, 0) dla t , więc żaden wykres nie wystarczy, aby pokryć cały okrąg. Można udowodnić, że jednym wykresem nie da się objąć pełnego koła. Na przykład, chociaż możliwe jest skonstruowanie okręgu z pojedynczego odcinka linii poprzez nakładanie się i „sklejanie” końców, nie tworzy to wykresu; część okręgu zostanie zmapowana na oba końce jednocześnie, tracąc odwracalność.
Kula
Kula jest przykładem powierzchni. Jednostka kuli z utajonego równaniem
- x 2 + y 2 + z 2 – 1 = 0
można objąć atlasem sześciu wykresów : płaszczyzna z = 0 dzieli kulę na dwie półkule ( z > 0 i z < 0 ), które mogą być odwzorowane na dysku x 2 + y 2 < 1 przez rzut na płaszczyźnie współrzędnych xy . Zapewnia to dwa wykresy; cztery pozostałe wykresy mają podobną konstrukcję z dwoma pozostałymi płaszczyznami współrzędnych.
W przypadku koła można zdefiniować jeden wykres obejmujący całą sferę z wyłączeniem jednego punktu. Wystarczą więc dwa wykresy, ale sfery nie da się objąć pojedynczym wykresem.
Ten przykład ma znaczenie historyczne, ponieważ umotywował terminologię; stało się jasne, że cała powierzchnia Ziemi nie może mieć odwzorowania płaskiego składającego się z jednej mapy (zwanej także „ mapą ”, patrz mapa morska ), dlatego do pokrycia całej powierzchni Ziemi potrzebny jest atlas .
Inne krzywe
Rozdzielacze nie muszą być połączone (wszystko w jednym kawałku); przykładem jest para oddzielnych kółek.
Rozdzielacze nie muszą być zamknięte ; zatem odcinek linii bez punktów końcowych jest rozmaitością. Nigdy nie są policzalne , chyba że wymiar rozmaitości wynosi 0. Łącząc te swobody, innymi przykładami rozmaitości są parabola , hiperbola , oraz miejsce punktów na krzywej sześciennej y 2 = x 3 − x (pętla zamknięta kawałek i otwarty, nieskończony kawałek).
Jednak wykluczone są przykłady, takie jak dwa stykające się koła, które mają wspólny punkt, tworząc cyfrę 8; we wspólnym punkcie nie można stworzyć zadowalającego wykresu. Nawet przy zginaniu dozwolonym przez topologię, sąsiedztwo wspólnego punktu wygląda jak „+”, a nie linia. „+” nie jest homeomorficzny z odcinkiem linii, ponieważ usunięcie punktu środkowego z „+” daje spację z czterema składnikami (tj. kawałkami), podczas gdy usunięcie punktu z odcinka daje spację z co najwyżej dwoma kawałkami; operacje topologiczne zawsze zachowują liczbę sztuk.
Definicja matematyczna
Nieformalnie rozmaitość jest przestrzenią „wzorowaną” na przestrzeni euklidesowej.
Istnieje wiele różnych rodzajów rozmaitości. W geometrii i topologii wszystkie rozmaitości są rozmaitościami topologicznymi , ewentualnie z dodatkową strukturą. Rozmaitość można skonstruować przez nadanie zbioru wykresów współrzędnych, tj. pokrycie przestrzeni euklidesowej zbiorami otwartymi z homeomorfizmami oraz funkcje łatania: homeomorfizmy z jednego regionu przestrzeni euklidesowej do innego regionu, jeśli odpowiadają tej samej części przestrzeni euklidesowej. rozmaitość na dwóch różnych wykresach współrzędnych. Rozmaitości można nadać dodatkową strukturę, jeśli funkcje krosowania spełniają aksjomaty poza ciągłością. Na przykład, rury rozgałęźne rozróżnialne mają homeomorfizmy na nakładających okolic diffeomorphic ze sobą, tak, że rozdzielacz ma dobrze określony zestaw funkcji, które są w każdym różniczkowalną sąsiedztwie, co różniczkowalną na zespole jako całości.
Formalnie rozmaitość (topologiczna) jest drugą policzalną przestrzenią Hausdorffa, która jest lokalnie homeomorficzna z przestrzenią euklidesową.
Druga policzalna i Hausdorff są warunkami zbioru punktowego ; druga policzalna wyklucza przestrzenie, które są w pewnym sensie „zbyt duże”, takie jak długa linia , podczas gdy Hausdorff wyklucza przestrzenie, takie jak „prosta o dwóch początkach” (te uogólnienia rozmaitości są omawiane w rozmaitościach innych niż Hausdorff ).
Lokalnie homeomorficzny z przestrzenią euklidesową oznacza, że każdy punkt ma sąsiedztwo homeomorficzne z otwartą n- kulą euklidesową ,
Ogólnie przyjmuje się, że rozmaitości mają ustalony wymiar (przestrzeń musi być lokalnie homeomorficzna do ustalonej n -kuli) i taką przestrzeń nazywamy n -rozmaitością ; jednak niektórzy autorzy dopuszczają rozmaitości, w których różne punkty mogą mieć różne wymiary . Jeśli rozmaitość ma stały wymiar, nazywa się ją czystą rozmaitością . Na przykład (powierzchnia a) kuli ma stały wymiar równy 2 i dlatego jest czystą rozmaitością, podczas gdy rozłączne połączenie kuli i prostej w przestrzeni trójwymiarowej nie jest czystą rozmaitością. Ponieważ wymiar jest niezmiennikiem lokalnym (tzn. mapa wysyłająca każdy punkt do wymiaru jego sąsiedztwa, na którym definiowany jest wykres, jest lokalnie stała ), każdy połączony składnik ma wymiar stały.
teoretycznie schematycznie jest przestrzenią lokalnie otoczoną , której snop struktury jest lokalnie izomorficzny ze snopem funkcji ciągłych (lub różniczkowalnych, zespolonych, itp.) na przestrzeni euklidesowej. Definicja ta jest najczęściej używana przy omawianiu rozmaitości analitycznych w geometrii algebraicznej .Wykresy, atlasy i mapy przejść
Nawigacja po kulistej Ziemi odbywa się za pomocą płaskich map lub wykresów, zebranych w atlasie. Podobnie rozmaitość różniczkowalna może być opisana za pomocą map matematycznych , zwanych wykresami współrzędnych , zebranych w atlasie matematycznym . Generalnie nie jest możliwe opisanie rozmaitości tylko jednym wykresem, ponieważ globalna struktura rozmaitości różni się od prostej struktury wykresów. Na przykład żadna pojedyncza płaska mapa nie może reprezentować całej Ziemi bez rozdzielenia sąsiednich obiektów w granicach mapy lub powielania pokrycia. Kiedy rozmaitość jest zbudowana z wielu nakładających się wykresów, regiony, w których się pokrywają, zawierają informacje niezbędne do zrozumienia globalnej struktury.
Wykresy
Mapa współrzędnych , wykres współrzędnych lub po prostu wykres , rozmaitości to odwracalna mapa między podzbiorem rozmaitości a prostą przestrzenią, tak że zarówno mapa, jak i jej odwrotność zachowują pożądaną strukturę. W przypadku rozmaitości topologicznej przestrzeń prosta jest podzbiorem pewnej przestrzeni euklidesowej, a zainteresowanie skupia się na strukturze topologicznej. Struktura ta jest zachowana przez
homeomorfizmy , odwracalne mapy, które są ciągłe w obu kierunkach.W przypadku rozmaitości różniczkowej zestaw wykresów zwany atlasem pozwala na wykonanie rachunku różniczkowego na rozmaitościach. Na przykład współrzędne biegunowe tworzą wykres płaszczyzny minus dodatnia oś
x i początek. Innym przykładem wykresu jest mapa χ top wspomniano powyżej, wykres dla okręgu.Atlasy
Opis większości rozmaitości wymaga więcej niż jednego wykresu. Specyficzny zbiór wykresów obejmujący rozmaitość nazywa się atlasem . Atlas nie jest wyjątkowy, ponieważ wszystkie rozmaitości można pokryć na wiele sposobów, używając różnych kombinacji wykresów. Mówi się, że dwa atlasy są równoważne, jeśli ich połączenie jest również atlasem.
Atlas zawierający wszystkie możliwe wykresy zgodne z danym atlasem nazywany jest atlasem maksymalnym (czyli klasą równoważności zawierającą ten atlas). W przeciwieństwie do zwykłego atlasu, atlas maksymalny danej rozmaitości jest unikalny. Choć przydatny do definicji, jest obiektem abstrakcyjnym i nie jest używany bezpośrednio (np. w obliczeniach).
Mapy przejść
Wykresy w atlasie mogą zachodzić na siebie, a pojedynczy punkt rozmaitości może być reprezentowany na kilku wykresach. Jeśli dwa wykresy nakładają się na siebie, ich części reprezentują ten sam obszar rozmaitości, tak jak mapa Europy i mapa Azji mogą zawierać Moskwę. Biorąc pod uwagę dwa nakładające się wykresy, można zdefiniować funkcję przejścia, która przechodzi od otwartej kuli do rozmaitości, a następnie z powrotem do innej (lub być może tej samej) otwartej kuli w . Mapa wynikowa, podobnie jak mapa
T w powyższym przykładzie okręgu, nazywana jest zmianą współrzędnych , transformacją współrzędnych , funkcją przejścia lub mapą przejścia .Dodatkowa struktura
Atlas może być również użyty do zdefiniowania dodatkowej struktury na kolektorze. Struktura jest najpierw definiowana na każdym wykresie osobno. Jeśli wszystkie mapy przejść są kompatybilne z tą strukturą, struktura przechodzi do rozmaitości.
Jest to standardowy sposób definiowania rozmaitości różniczkowalnych. Jeśli funkcje przejścia atlasu dla rozmaitości topologicznej zachowują naturalną strukturę różniczkową (to znaczy, jeśli są
dyfeomorfizmami ), to struktura różniczkowa przechodzi do rozmaitości i przekształca ją w rozmaitość różniczkowalną. Rozmaitości zespolone są wprowadzane w analogiczny sposób, wymagając, aby funkcje przejścia atlasu były funkcjami holomorficznymi . W przypadku rozmaitości symplektycznych funkcje przejścia muszą być symplektomorfizmami .Struktura na rozmaitości zależy od atlasu, ale czasami można powiedzieć, że różne atlasy dają początek tej samej strukturze. Takie atlasy nazywane są kompatybilnymi .
Pojęcia te są na ogół sprecyzowane przez użycie pseudogrup .
Rozmaitość z granicą
Kolektor z granicą jest kolektor z krawędzią. Na przykład kartka papieru to dwurozmaitość z jednowymiarową granicą. Granica n -rozmaitości z granicą to ( n -1) -rozmaitość. Dysku (kółko oraz wewnętrzny) jest 2-kolektor z granica. Jej granicą jest okrąg, 1-rozmaitość . Kwadratowy z wnętrza jest także 2-kolektor z granica. Kulki (sfery oraz wewnętrzny) jest 3-kolektor z granica. Jej granica to kula, podwójna rozmaitość. (Zobacz także Granica (topologia) ).
W języku technicznym rozmaitość z granicą to przestrzeń zawierająca zarówno punkty wewnętrzne, jak i punkty graniczne. Każdy punkt wewnętrzny ma homeomorficzne sąsiedztwo otwartej kuli n {( x 1 , x 2 , ..., x n ) | Σ x i 2 < 1}. Każdy punkt graniczny ma homeomorficzne sąsiedztwo dla "połówki" n- kuli {( x 1 , x 2 , ..., x n ) | Σ x i 2 < 1 i x 1 ≥ 0} . Homeomorfizm musi wysłać każdy punkt graniczny do punktu, w którym x 1 = 0.
Granica i wnętrze
Niech M będzie rozmaitością z brzegiem. Wnętrze z M , oznaczoną Int M jest zbiorem punktów M które okolic homeomorficzny otwartym podzbioru .
Granicy z M , oznaczoną ∂ M , jest dopełnieniem int M w M . Punkty graniczne można scharakteryzować tych punktów, które lądują na hiperpłaszczyznę granicy ( x n = 0), na podstawie niektórych wykres współrzędnych.Jeśli M jest rozmaitością z brzegiem wymiaru n , to Int
M jest rozmaitością (bez brzegu) wymiaru n , a ∂ M jest rozmaitością (bez brzegu) wymiaru n − 1 .Budowa
Pojedynczy kolektor może być skonstruowany na różne sposoby, z których każdy podkreśla inny aspekt kolektora, prowadząc w ten sposób do nieco innego punktu widzenia.
Wykresy
Być może najprostszym sposobem skonstruowania rozmaitości jest ten użyty w powyższym przykładzie koła. Najpierw identyfikowany jest podzbiór , a następnie tworzony jest atlas obejmujący ten podzbiór. Pojęcie
rozmaitości wyrosło historycznie z takich konstrukcji. Oto kolejny przykład zastosowania tej metody do konstrukcji kuli:Kula z wykresami
Kulę można traktować prawie tak samo jak koło. W matematyce kula to tylko powierzchnia (nie wnętrze bryły), którą można zdefiniować jako podzbiór :
Kula jest dwuwymiarowa, więc każdy wykres odwzorowuje część kuli na otwarty podzbiór . Weźmy pod uwagę półkulę północną, która jest częścią o dodatniej współrzędnej
z (kolor czerwony na zdjęciu po prawej). Funkcja χ zdefiniowana przezmapuje półkulę północną na dysk jednostki otwartej
, rzutując ją na płaszczyznę ( x , y ). Podobny wykres istnieje dla półkuli południowej. Wraz z dwoma mapami rzutowanymi na płaszczyznę ( x , z ) i dwoma mapami rzutowanymi na płaszczyznę ( y , z ) otrzymujemy atlas sześciu map obejmujących całą sferę.Można to łatwo uogólnić na sfery o wyższych wymiarach.
Niejednolita całość
Rozdzielacz można zbudować, sklejając ze sobą elementy w spójny sposób, tworząc z nich zachodzące na siebie wykresy. Taka konstrukcja jest możliwa dla dowolnej rozmaitości i dlatego jest często używana jako charakterystyka, zwłaszcza dla rozmaitości różniczkowalnych i riemannowskich. Koncentruje się na atlasie, ponieważ łaty w naturalny sposób dostarczają wykresów, a ponieważ nie ma w tym żadnej przestrzeni zewnętrznej, prowadzi to do wewnętrznego spojrzenia na rozmaitość.
Rozmaitość jest tworzona przez określenie atlasu, który sam jest definiowany przez mapy przejść. Punkt rozmaitości jest zatem klasą równoważności punktów, które są odwzorowywane na siebie przez mapy przejść. Wykresy odwzorowują klasy równoważności do punktów pojedynczej łatki. Zwykle istnieją silne wymagania dotyczące spójności map przejść. W przypadku rozmaitości topologicznych muszą być homeomorfizmami; jeśli są one również dyfeomorfizmami, wynikowa rozmaitość jest rozmaitością różniczkowalną.
Można to zilustrować mapą przejść t = 1 ⁄ s z drugiej połowy przykładu okręgu. Zacznij od dwóch kopii linii. Użyj współrzędnych s dla pierwszej kopii, t dla drugiej kopii. Teraz sklej obie kopie razem, identyfikując punkt t na drugiej kopii z punktem s = 1 ⁄ t na pierwszej kopii (punkty t = 0 i s = 0 nie są utożsamiane z żadnym punktem na pierwszej i drugiej kopii, odpowiednio). To daje krąg.
Widok wewnętrzny i zewnętrzny
Pierwsza konstrukcja i ta konstrukcja są bardzo podobne, ale reprezentują raczej różne punkty widzenia. W pierwszej konstrukcji rozmaitość jest postrzegana jako osadzona w jakiejś przestrzeni euklidesowej. To jest zewnętrzny widok . Patrząc na rozmaitość w ten sposób, łatwo jest posłużyć się intuicją z przestrzeni euklidesowych do zdefiniowania dodatkowej struktury. Na przykład w przestrzeni euklidesowej zawsze jest jasne, czy wektor w pewnym punkcie jest styczny czy normalny do jakiejś powierzchni przechodzącej przez ten punkt.
Patchworkowa konstrukcja nie wykorzystuje żadnego osadzenia, a jedynie postrzega rozmaitość jako samą w sobie przestrzeń topologiczną. Ten abstrakcyjny punkt widzenia nazywany jest poglądem wewnętrznym . Może to utrudnić wyobrażenie sobie, czym może być wektor styczny, i nie ma wewnętrznego pojęcia normalnej wiązki, ale zamiast tego istnieje samoistnie stabilna normalna wiązka .
n -Sfera jako patchwork
N -sphere S n jest uogólnieniem idei koła (1) i kula kuli (sfery), 2 do większych wymiarach. N -sphere S n może być wykonana poprzez sklejenie ze sobą dwóch kopii . Mapą przejścia między nimi jest
inwersja w sferze , zdefiniowana jakoTa funkcja jest swoją odwrotnością i dlatego może być używana w obu kierunkach. Ponieważ mapa przejścia jest funkcją gładką , atlas ten definiuje gładką rozmaitość. W przypadku n = 1 przykład upraszcza się do podanego wcześniej przykładu koła.
Identyfikacja punktów rozmaitości
Możliwe jest zdefiniowanie różnych punktów rozmaitości, aby były takie same. Można to zobrazować jako sklejenie tych punktów w jeden punkt, tworząc przestrzeń ilorazową . Nie ma jednak powodu, by oczekiwać, że takie przestrzenie ilorazowe będą rozmaitościami. Wśród możliwych przestrzeni ilorazowych, które niekoniecznie są rozmaitościami, orbifoldy i kompleksy CW są uważane za stosunkowo dobrze zachowane . Przykładem przestrzeni ilorazowej rozmaitości będącej jednocześnie rozmaitością jest rzeczywista przestrzeń rzutowa , identyfikowana jako przestrzeń ilorazowa odpowiedniej sfery.
Jednym ze sposobów identyfikowania punktów (sklejania ich) jest prawe (lub lewe) działanie grupy , która działa na rozmaitość. Dwa punkty są identyfikowane, jeśli jeden z nich zostanie przesunięty przez jakiś element grupy. Jeśli M jest rozmaitością, a G grupą, to powstała przestrzeń ilorazowa jest oznaczona przez M / G (lub G \ M ).
Rozmaitości, które można skonstruować poprzez identyfikację punktów, obejmują tori i rzeczywiste przestrzenie rzutowe (zaczynające się odpowiednio od płaszczyzny i kuli).
Klejenie wzdłuż granic
Wzdłuż granicy można skleić ze sobą dwie kolektory z granicami. Jeśli zostanie to zrobione we właściwy sposób, wynik jest również rozmaity. Podobnie można skleić ze sobą dwie granice jednego kolektora.
Formalnie klejenie jest określone przez bijekcję między dwiema granicami. Dwa punkty są identyfikowane, gdy są na siebie nanoszone. W przypadku rozmaitości topologicznej ta bijekcja powinna być homeomorfizmem, w przeciwnym razie wynikiem nie będzie rozmaitość topologiczna. Podobnie dla rozmaitości różniczkowej musi to być dyfeomorfizm. W przypadku innych kolektorów należy zachować inne struktury.
Skończony cylinder może być skonstruowany jako kolektor, zaczynając od paska [0,1] × [0,1] i sklejając parę przeciwległych krawędzi na granicy za pomocą odpowiedniego dyfeomorfizmu. Rzutowa płaszczyzna może być uzyskane przez sklejenie kulę z otworem w środku do taśmy Möbius wzdłuż swych granic okrągłych.
Produkty kartezjańskie
Iloczyn kolektorów jest także wielorakie.
Wymiar rozmaitości produktu jest sumą wymiarów jego czynników. Jego topologia to topologia produktu , a iloczyn kartezjański wykresów to wykres dla kolektora produktu. W ten sposób atlas dla rozmaitości produktu może być skonstruowany przy użyciu atlasów dla jego współczynników. Jeśli te atlasy definiują strukturę różniczkową na czynnikach, odpowiedni atlas definiuje strukturę różniczkową na rozmaitości produktów. To samo dotyczy każdej innej struktury zdefiniowanej na podstawie czynników. Jeżeli jeden z czynników ma granicę, to rozmaitość produktów również ma granicę. Produkty kartezjańskie mogą być używane do budowy tori i cylindrów skończonych , na przykład odpowiednio jako S 1 × S 1 i S 1 × [0,1].
Historia
Badanie rozmaitości łączy wiele ważnych dziedzin matematyki: uogólnia pojęcia, takie jak krzywe i powierzchnie, a także idee algebry liniowej i topologii.
Wczesny rozwój
Przed nowoczesną koncepcją rozmaitości było kilka ważnych wyników.
Geometria nieeuklidesowa uważa przestrzenie, w których Euklides „s równoległy postulat zawiedzie. Saccheri po raz pierwszy badał takie geometrie w 1733 roku, ale starał się je tylko obalić. Gauss , Bolyai i Lobachevsky niezależnie odkryli je 100 lat później. Ich badania ujawniły dwa typy przestrzeni, których struktura geometryczna różni się od klasycznej przestrzeni euklidesowej; dały one początek geometrii hiperbolicznej i geometrii eliptycznej . We współczesnej teorii rozmaitości pojęcia te odpowiadają rozmaitościom riemannowskim o stałej , odpowiednio, ujemnej i dodatniej krzywiźnie .
Carl Friedrich Gauss mógł być pierwszym, który uznał przestrzenie abstrakcyjne za same w sobie obiekty matematyczne. Jego twierdzenie egregium podaje metodę obliczania krzywizny powierzchni bez uwzględniania otaczającej przestrzeni, w której leży powierzchnia. Taka powierzchnia byłaby we współczesnej terminologii nazwana rozmaitością; a we współczesnym ujęciu twierdzenie dowiodło, że krzywizna powierzchni jest właściwością samoistną . Teoria rozmaitości zaczęła skupiać się wyłącznie na tych wewnętrznych właściwościach (lub niezmiennikach), jednocześnie w dużej mierze ignorując zewnętrzne właściwości otaczającej przestrzeni.
Innym, bardziej topologicznym przykładem wewnętrznej własności rozmaitości jest jej charakterystyka Eulera . Leonhard Euler wykazał, że dla wypukłego politopu w trójwymiarowej przestrzeni euklidesowej z
wierzchołkami V (lub narożnikami), krawędziami E i ścianami F ,Synteza
Badania Nielsa Henrika Abla i Carla Gustava Jacobiego dotyczące odwrócenia całek eliptycznych w pierwszej połowie XIX wieku doprowadziły ich do rozważenia specjalnych typów rozmaitości zespolonych, znanych obecnie jako jakobiany . Bernhard Riemann wniósł dalszy wkład do ich teorii, wyjaśniając geometryczne znaczenie procesu analitycznego kontynuacji funkcji zmiennych zespolonych.
Innym ważnym źródłem rozmaitości w dziewiętnastowiecznej matematyce była mechanika analityczna , opracowana przez Siméona Poissona , Jacobiego i Williama Rowana Hamiltona . Za możliwe stany układu mechanicznego uważa się punkty przestrzeni abstrakcyjnej, przestrzeni fazowej w formalizmach Lagrange'a i Hamiltona mechaniki klasycznej. Przestrzeń ta jest w rzeczywistości wielowymiarową rozmaitością, której wymiar odpowiada stopniom swobody układu i gdzie punkty są określone przez ich uogólnione współrzędne . Dla swobodnego ruchu cząstek swobodnych rozmaitość jest równoważna przestrzeni euklidesowej, ale różne prawa zachowania ograniczają ją do bardziej skomplikowanych formacji, np. Liouville tori . Teoria obracającego się ciała stałego, opracowana w XVIII wieku przez Leonharda Eulera i Josepha-Louisa Lagrange'a , daje kolejny przykład, w którym rozmaitość nie jest trywialna. Geometryczne i topologiczne aspekty mechaniki klasycznej zostały podkreślone przez Henri Poincaré , jednego z twórców topologii.
Riemann jako pierwszy wykonał obszerną pracę uogólniającą ideę powierzchni na wyższe wymiary. Rozmaitość nazwy pochodzi od oryginalnego niemieckiego terminu Riemanna , Mannigfaltigkeit , który William Kingdon Clifford przetłumaczył jako „rozmaitość”. W swoim inauguracyjnym wykładzie w Getyndze Riemann opisał zbiór wszystkich możliwych wartości zmiennej z pewnymi ograniczeniami jako Mannigfaltigkeit , ponieważ zmienna może mieć wiele wartości. Rozróżnia on stetige Mannigfaltigkeit i disckrete Mannigfaltigkeit ( rozmaitość ciągła i nieciągła ), w zależności od tego, czy wartość zmienia się w sposób ciągły, czy nie. Jako ciągłe przykłady Riemann odwołuje się nie tylko do kolorów i rozmieszczenia obiektów w przestrzeni, ale także do możliwych kształtów figury przestrzennej. Korzystając z indukcji , Riemann konstruuje n-fach ausgedehnte Mannigfaltigkeit ( n razy rozszerzoną rozmaitość lub n-wymiarową rozmaitość ) jako ciągły stos (n−1) rozmaitości wymiarowych. Intuicyjne pojęcie Mannigfaltigkeit Riemanna ewoluowało w to, co dziś jest sformalizowane jako rozmaitość. Rozmaitości riemannowskie i powierzchnie Riemanna noszą nazwy Riemanna.
Definicja Poincare
W swoim bardzo wpływowym artykule, Analysis Situs , Henri Poincaré podał definicję rozmaitości różniczkowej ( variété ), która służyła jako prekursor nowoczesnej koncepcji rozmaitości.
W pierwszej części Analysis Situs, Poincaré definiuje rozmaitość jako zbiór poziomów ciągle różniczkowalnej funkcji między przestrzeniami euklidesowymi, który spełnia hipotezę niezdegeneracji twierdzenia o funkcji utajonej . W trzeciej części zaczyna od spostrzeżenia, że wykres funkcji ciągle różniczkowalnej jest rozmaitością w tym drugim znaczeniu. Następnie proponuje nową, bardziej ogólną definicję rozmaitości opartą na „łańcuchu rozmaitości” ( une chaîne des variétés ).
Pojęcie łańcucha rozmaitości Poincarégo jest prekursorem nowoczesnego pojęcia atlasu. W szczególności rozważa dwie rozmaitości zdefiniowane odpowiednio jako wykresy funkcji i . Jeśli te rozmaitości nakładają się na siebie (
a une partie commune ), to wymaga, aby współrzędne w sposób ciągły różniły się od współrzędnych i vice versa („ …les sont fonctions analytiques des et inversement ”). W ten sposób wprowadza prekursora pojęcia wykresu i mapy przejścia .Na przykład okrąg jednostkowy na płaszczyźnie można traktować jako wykres funkcji lub funkcję w sąsiedztwie każdego punktu z wyjątkiem punktów (1, 0) i (-1, 0); aw sąsiedztwie tych punktów można go traktować jako wykres odpowiednio i . Okrąg może być reprezentowany przez wykres w sąsiedztwie każdego punktu, ponieważ lewa strona równania definiującego ma niezerowy gradient w każdym punkcie okręgu. Zgodnie z
twierdzeniem o funkcji uwikłanej każdy podrozmaitość przestrzeni euklidesowej jest lokalnie grafem funkcji.Hermann Weyl podał wewnętrzną definicję rozmaitości różniczkowych w swoim kursie na powierzchniach Riemanna w latach 1911-1912, otwierając drogę do ogólnej koncepcji przestrzeni topologicznej, która nastąpiła wkrótce. W latach trzydziestych Hassler Whitney i inni wyjaśnili fundamentalne aspekty tego tematu, dzięki czemu intuicje sięgające drugiej połowy XIX wieku stały się precyzyjne i rozwinięte dzięki geometrii różniczkowej i teorii grup Liego . Warto zauważyć, że twierdzenie Whitneya o osadzeniu pokazało, że wewnętrzna definicja pod względem wykresów była równoważna definicji Poincarégo pod względem podzbiorów przestrzeni euklidesowej.
Topologia rozmaitości: najważniejsze informacje
Rozmaitości dwuwymiarowe, znane również jako powierzchnie 2D osadzone w naszej wspólnej przestrzeni 3D, były rozważane przez Riemanna pod przykrywką powierzchni Riemanna i rygorystycznie klasyfikowane na początku XX wieku przez Poula Heegaarda i Maxa Dehna . Poincaré był pionierem badań nad rozmaitościami trójwymiarowymi i postawił na ich temat fundamentalne pytanie, znane dziś jako hipoteza Poincarégo . Po prawie stuleciu Grigori Perelman udowodnił hipotezę Poincarégo (patrz Rozwiązanie hipotezy Poincarégo ). William Thurston „s Program geometryzacja , sformułowana w 1970 roku, pod warunkiem daleko idące rozszerzenie hipotezy Poincaré ogólnych rozmaitości trójwymiarowych. Rozmaitości czterowymiarowe zostały wprowadzone na czoło badań matematycznych w latach 80. XX wieku przez Michaela Freedmana, a w innym kontekście przez Simona Donaldsona , który był motywowany niedawnym postępem w fizyce teoretycznej ( teoria Yang-Millsa ), gdzie służą jako namiastka zwykłej „płaskiej” czasoprzestrzeni . Andrey Markov Jr. wykazał w 1960 r., że nie istnieje żaden algorytm klasyfikacji wielowymiarowych rozmaitości. Ważną pracę nad wielowymiarowymi rozmaitościami, w tym analogami hipotezy Poincarégo , wykonali wcześniej René Thom , John Milnor , Stephen Smale i Sergei Novikov . Bardzo wszechobecną i elastyczną techniką leżącą u podstaw wielu prac nad topologią rozmaitości jest teoria Morse'a .
Dodatkowa struktura
Rozmaitości topologiczne
Najprostszym rodzajem rozmaitości do zdefiniowania jest rozmaitość topologiczna, która lokalnie wygląda jak „zwykła” przestrzeń euklidesowa . Z definicji wszystkie rozmaitości są rozmaitościami topologicznymi, więc wyrażenie „rozmaitość topologiczna” jest zwykle używane do podkreślenia, że rozmaitość nie ma dodatkowej struktury lub że rozważane są tylko jej własności topologiczne. Formalnie rozmaitość topologiczna jest przestrzenią topologiczną
lokalnie homeomorficzną z przestrzenią euklidesową. Oznacza to, że każdy punkt ma sąsiedztwo, dla którego istnieje homeomorfizm ( bijective ciągłej funkcji, której odwrotność jest również ciągła) odwzorowujące to sąsiedztwo na . Te homeomorfizmy są wykresami rozmaitości.A topologiczne różnorodne spojrzenia lokalnie jak przestrzeni euklidesowej w dość słabym sposób: podczas gdy dla każdego wykresu możliwe jest rozróżnienie różniczkowalna funkcji lub Pomiar odległości i kątów, jedynie z racji bycia topologiczną kolektor przestrzeń nie ma szczególności i spójne wybór takich koncepcji. Aby omówić takie własności dla rozmaitości, należy określić dalszą strukturę i rozważyć rozmaitości różniczkowe oraz omówione poniżej rozmaitości riemannowskie . W szczególności, ta sama leżąca u podstaw rozmaitość topologiczna może mieć kilka wzajemnie niekompatybilnych klas funkcji różniczkowalnych oraz nieskończoną liczbę sposobów określania odległości i kątów.
Zwykle podejmuje się dodatkowe założenia techniczne dotyczące przestrzeni topologicznej, aby wykluczyć przypadki patologiczne. Zwyczajowo wymaga się, aby przestrzeń była Hausdorff i druga policzalna .
Wymiar kolektora w określonym miejscu jest wymiar euklidesowej przestrzeni wykresy w tym punkcie na mapie (liczba N w definicji). Wszystkie punkty w połączonej rozmaitości mają ten sam wymiar. Niektórzy autorzy wymagają, aby wszystkie wykresy topologicznej rozmaitości odwzorowywały przestrzenie euklidesowe o tym samym wymiarze. W takim przypadku każda rozmaitość topologiczna ma topologiczny niezmiennik, swój wymiar.
Rozmaitości różniczkowe
W większości zastosowań stosuje się specjalny rodzaj rozmaitości topologicznej, a mianowicie rozmaitość różniczkowalną . Jeśli lokalne mapy na rozmaitości są w pewnym sensie kompatybilne, można na tej rozmaitości określić kierunki, przestrzenie styczne i funkcje różniczkowalne. W szczególności możliwe jest zastosowanie rachunku różniczkowego na rozmaitości różniczkowej. Każdy punkt n- wymiarowej rozmaitości różniczkowej ma przestrzeń styczną . Jest to n- wymiarowa przestrzeń euklidesowa składająca się z wektorów stycznych krzywych przechodzących przez punkt.
Dwie ważne klasy rozmaitości różniczkowych to rozmaitości gładkie i analityczne . Dla gładkich rozmaitości mapy przejść są gładkie, to znaczy nieskończenie różniczkowalne. Rozmaitości analityczne są rozmaitościami gładkimi z dodatkowym warunkiem, że mapy przejść są analityczne (mogą być wyrażone jako szeregi potęgowe ). Sferze można nadać strukturę analityczną, podobnie jak większość znanych krzywych i powierzchni.
Zbiór korygujący uogólnia ideę odcinkowo gładkiej lub korygującej krzywej do wyższych wymiarów; jednak zbiory poprawialne nie są w rozmaitościach ogólnych.
Rozmaitości riemannowskie
Aby zmierzyć odległości i kąty na rozmaitościach, rozmaitość musi być riemannowska. Riemanna kolektor jest różniczkowalną kolektora, w którym każda przestrzeń styczna jest wyposażony w produkcie wewnętrznej ⟨⋅, ⋅⟩ w sposób, który zmienia się płynnie od punktu do punktu. Mając dwa wektory styczne u i v , iloczyn skalarny ⟨ u , v ⟩ daje liczbę rzeczywistą. Punkt (lub skalarne) produkt jest typowym przykładem produktu wewnętrznej. Pozwala to na zdefiniowanie różnych pojęć takich jak długość, prostym , obszary (lub objętości ) krzywizny i rozbieżności w dziedzinie wektorów .
Wszystkim rozmaitościom różniczkowalnym (o stałym wymiarze) można nadać strukturę rozmaitości riemannowskiej. Sama przestrzeń euklidesowa niesie naturalną strukturę rozmaitości riemannowskiej (przestrzenie styczne są naturalnie utożsamiane z samą przestrzenią euklidesową i zawierają standardowy iloczyn skalarny tej przestrzeni). Wiele znanych krzywych i powierzchni, w tym na przykład wszystkie n -sfery, określa się jako podprzestrzenie przestrzeni euklidesowej i dziedziczy metrykę z ich osadzenia w niej.
Rozdzielacze Finslera
Finsler kolektora umożliwia określenie odległości, ale nie wymaga pojęcie kąta; jest to rozmaitość analityczna, w której każda przestrzeń styczna jest wyposażona w normę , ||·||, w sposób płynnie zmieniający się z punktu do punktu. Normę tę można rozszerzyć do metryki , określając długość krzywej; ale generalnie nie można go używać do definiowania iloczynu skalarnego.
Każda rozmaitość Riemanna jest rozmaitością Finslera.
Grupy kłamstw
Grupy Liego , nazwane imieniem Sophusa Liego , są rozmaitościami różniczkowymi, które mają również strukturę grupy, która jest taka, że operacje grupowe są definiowane przez gładkie odwzorowania.
Przestrzeń euklidesowa z operacją grupową dodawania wektorów jest przykładem niezwartej grupy Liego. Prostym przykładem zwartej grupy Liego jest koło: operacja grupowa to po prostu rotacja. Grupę tę, znaną jako U(1), można również scharakteryzować jako grupę liczb zespolonych o module 1 z mnożeniem jako działaniem grupowym.
Inne przykłady grup Liego obejmują specjalne grupy macierzy , które są wszystkimi podgrupami ogólnej grupy liniowej , grupy macierzy n na n z niezerowym wyznacznikiem. Jeśli wpisy macierzy są liczbami rzeczywistymi , będzie to n 2- wymiarowa rozmaitość niepołączona. W ortogonalne grupy , gdy grupa symetrii sfery i hyperspheres , to n ( n -1) / 2, gdzie kolektory wymiarowe n -1 wymiar kuli. Dalsze przykłady można znaleźć w tabeli grup Liego .
Inne typy kolektorów
- Kompleks kolektor jest kolektor którego wykresy przyjmować wartości w i których funkcje przejście są
Klasyfikacja i niezmienniki
Różne pojęcia rozmaitości mają różne pojęcia klasyfikacji i niezmiennika; w tej sekcji skupiamy się na gładkich, zamkniętych kolektorach.
Klasyfikacja gładkich zamkniętych rozmaitości jest w zasadzie dobrze zrozumiana , z wyjątkiem wymiaru 4 : w niskich wymiarach (2 i 3) jest geometryczna, poprzez twierdzenie o uniformizacji i rozwiązanie hipotezy Poincarégo , oraz w wysokim wymiarze (5 i powyżej) to jest algebraiczne, poprzez teorię chirurgiczną . Jest to w zasadzie klasyfikacja: ogólne pytanie, czy dwie gładkie rozmaitości są diffeomorficzne, nie jest ogólnie obliczalne. Co więcej, szczegółowe obliczenia pozostają trudne i istnieje wiele otwartych pytań.
Można wizualizować powierzchnie orientowalne, a ich klasy dyfeomorfizmu ponumerować według rodzaju. Mając dwie orientowalne powierzchnie, można określić, czy są one diffeomorficzne, obliczając ich odpowiednie rodzaje i porównując: są diffeomorficzne wtedy i tylko wtedy, gdy rodzaje są równe, więc rodzaj tworzy kompletny zestaw niezmienników .
Jest to o wiele trudniejsze w wyższych wymiarach: wielowymiarowych rozmaitości nie można bezpośrednio wizualizować (chociaż intuicja wizualna jest przydatna w ich zrozumieniu), nie można też wyliczyć ich klas dyfeomorfizmu, ani ogólnie nie można określić, czy dwa różne opisy rozmaitość odnoszą się do tego samego przedmiotu.
Można jednak określić, czy dwie rozmaitości są różne, jeśli istnieje jakaś wewnętrzna cecha, która je różnicuje. Takie kryteria są powszechnie określane jako niezmienniki , ponieważ chociaż można je zdefiniować w kategoriach jakiejś prezentacji (takiej jak rodzaj w kategoriach triangulacji), są one takie same w odniesieniu do wszystkich możliwych opisów konkretnej rozmaitości: są niezmienne pod różnymi opisami.
Naiwnie można by mieć nadzieję na opracowanie arsenału niezmiennych kryteriów, które definitywnie zaklasyfikowałyby wszystkie rozmaitości aż do izomorfizmu. Niestety wiadomo, że dla rozmaitości o wymiarze 4 i wyższych nie istnieje żaden program, który mógłby rozstrzygnąć, czy dwie rozmaitości są dyfeomorficzne.
Rozmaitości gładkie mają bogaty zestaw niezmienników , pochodzących z topologii zbioru punktowego , klasycznej topologii algebraicznej i topologii geometrycznej . Najbardziej znanymi niezmiennikami, które są widoczne dla powierzchni, są orientowalność (niezmiennik normalny, również wykrywany przez homologię ) i rodzaj (niezmiennicz homologiczny).
Gładkie, zamknięte rozmaitości nie mają lokalnych niezmienników (poza wymiarami), chociaż geometryczne rozmaitości mają lokalne niezmienniki, zwłaszcza krzywiznę rozmaitości riemannowskiej i skręcanie rozmaitości wyposażonej w połączenie afiniczne . To rozróżnienie między lokalnymi niezmiennikami i brakiem lokalnych niezmienników jest powszechnym sposobem odróżnienia geometrii od
topologii . Wszystkie niezmienniki gładko zamkniętej rozmaitości są zatem globalne.Topologia algebraiczna jest źródłem wielu ważnych globalnych niezmienniczych własności. Niektóre kluczowe kryteria obejmują po prostu połączoną właściwość i orientację (patrz poniżej). Rzeczywiście, powstało kilka gałęzi matematyki, takich jak teoria homologii i homotopii oraz teoria klas charakterystycznych , aby badać niezmienne własności rozmaitości.
Powierzchnie
Orientacyjność
W wymiarze drugim i wyższym prostym, ale ważnym kryterium niezmiennika jest pytanie, czy rozmaitość dopuszcza jakąś sensowną orientację. Rozważmy rozmaitość topologiczną z mapowaniem wykresów do . Mając
uporządkowaną podstawę dla , wykres powoduje, że jego fragment rozmaitości sam sobie nabiera sensu uporządkowania, które w 3 wymiarach może być postrzegane jako praworęczne lub lewoskrętne. Zachodzące na siebie wykresy nie muszą być zgodne w sensie uporządkowania, co daje rozmaitościom istotną swobodę. W przypadku niektórych rozmaitości, takich jak kula, wykresy mogą być wybrane tak, aby nakładające się regiony zgadzały się co do ich „ręczności”; są to rozmaitości orientowalne . Dla innych jest to niemożliwe. Ta ostatnia możliwość jest łatwa do przeoczenia, ponieważ każda zamknięta powierzchnia osadzona (bez samoprzecinania się) w przestrzeni trójwymiarowej jest orientowana.Niektóre ilustracyjne przykłady nieorientowalnych rozmaitości obejmują: (1) pasek Möbiusa , który jest rozmaitością z brzegiem, (2) butelkę Kleina , która musi przecinać się w swojej 3-przestrzennej reprezentacji oraz (3) rzeczywistą płaszczyznę rzutową , który pojawia się naturalnie w geometrii.
Wstęga Möbiusa
Zacznij od nieskończonego okrągłego cylindra stojącego pionowo, kolektora bez granic. Pokrój go wysoko i nisko, aby uzyskać dwie okrągłe granice i cylindryczny pasek między nimi. Jest to orientowalna rozmaitość z granicą, na której zostanie wykonana „operacja”. Rozetnij pasek tak, aby mógł się rozwinąć w prostokąt, ale trzymaj odcięte końce. Przekręć jeden koniec o 180 °, aby wewnętrzna powierzchnia była skierowana na zewnątrz, i sklej końce bezproblemowo. Daje to pasek z trwałym półskrętem: pasek Möbiusa. Jej granica nie jest już parą okręgów, ale (topologicznie) pojedynczym okręgiem; a to, co kiedyś było jego „wnętrzem”, połączyło się z „zewnątrz”, tak że teraz ma tylko jedną stronę. Podobnie jak poniżej Butelka Kleina, ta dwuwymiarowa powierzchnia musiałaby przecinać się w dwóch wymiarach, ale można ją łatwo skonstruować w trzech lub więcej wymiarach.
Butelka Kleina

Weź dwa paski Möbiusa; każdy ma pojedynczą pętlę jako granicę. Wyprostuj te pętle w kółka i pozwól, aby paski przekształciły się w krzyżyk . Sklejenie ze sobą kółek da nowy, zamknięty kolektor bez granic, butelkę Kleina. Zamknięcie powierzchni nie poprawia braku orientacji, a jedynie usuwa granicę. Tak więc butelka Kleina jest zamkniętą powierzchnią bez rozróżnienia na wnętrze i zewnętrze. W przestrzeni trójwymiarowej powierzchnia butelki Kleina musi przejść przez siebie. Zbudowanie butelki Kleina, która się nie krzyżuje, wymaga co najmniej czterech wymiarów przestrzeni.
Prawdziwa płaszczyzna rzutowa
Zacznij od kuli wyśrodkowanej na początku. Każda linia przechodząca przez początek przebija kulę w dwóch przeciwległych punktach zwanych antypodami . Chociaż fizycznie nie da się tego zrobić, możliwe jest (uwzględniając przestrzeń ilorazową ) matematyczne połączenie każdej pary antypodów w jeden punkt. Tak wytworzona zamknięta powierzchnia jest rzeczywistą płaszczyzną rzutową, jeszcze inną powierzchnią niemożliwą do orientowania. Ma wiele równoważnych opisów i konstrukcji, ale ta trasa wyjaśnia jej nazwę: wszystkie punkty na danej linii przez projekt początkowy do tego samego "punktu" na tej "płaszczyźnie".
Rodzaj i charakterystyka Eulera
W przypadku dwuwymiarowych rozmaitości kluczową niezmienną własnością jest rodzaj lub „liczba uchwytów” obecnych na powierzchni. Torus to kula z jednym uchwytem, podwójny torus to kula z dwoma uchwytami i tak dalej. Rzeczywiście, możliwe jest pełne scharakteryzowanie zwartych, dwuwymiarowych rozmaitości na podstawie rodzaju i możliwości orientacji. W wielowymiarowych rozmaitościach rodzaj zostaje zastąpiony pojęciem cechy Eulera , a bardziej ogólnie liczbami Bettiego oraz homologią i kohomologią .
Mapy rozmaitości
Tak jak istnieją różne typy rozmaitości, tak istnieją różne typy map rozmaitości . Oprócz funkcji ciągłych i ogólnie funkcji gładkich istnieją mapy o specjalnych właściwościach. W topologii geometrycznej podstawowym typem są zanurzenia , których centralnym przykładem jest teoria węzłów , oraz uogólnienia takie jak zanurzenia , zanurzenia , przestrzenie zakrywające i rozgałęzione przestrzenie zakrywające . Podstawowe wyniki obejmują twierdzenie Whitneya o osadzeniu i
twierdzenie Whitneya o zanurzeniu .W geometrii Riemanna, można poprosić o mapach do zachowania się metrykę Riemanna, co prowadzi do pojęcia izometrycznych zanurzeń , izometrycznych immersions i riemannowskiej zanurzenia ; podstawowym wynikiem jest twierdzenie Nasha o osadzeniu .
Funkcje o wartościach skalarnych
Podstawowym przykładem odwzorowań między rozmaitościami są skalarne funkcje na rozmaitości,
czasami nazywane regularnymi funkcjami lub funkcjonałami , przez analogię z geometrią algebraiczną lub algebrą liniową. Są one interesujące zarówno same w sobie, jak i w celu zbadania leżącej u ich podstaw różnorodności.
W topologii geometrycznej najczęściej badane są funkcje Morse'a , które dają dekompozycje korpusów uchwytów , podczas gdy w analizie matematycznej często bada się rozwiązania równań różniczkowych cząstkowych , których ważnym przykładem jest analiza harmoniczna , w której bada się funkcje harmoniczne : jądro Laplace'a operator . Prowadzi to do takich funkcji, jak harmoniczne sferyczne , oraz do podgrzewania jądra metod badania rozmaitości, takich jak słuchanie kształtu bębna i niektórych dowodów twierdzenia o indeksie Atiyaha-Singera .
Uogólnienia rozmaitości
- Rozmaitości nieskończenie wymiarowe
- Definicję rozmaitości można uogólnić, odrzucając wymóg skończonej wymiarowości. Zatem nieskończona rozmaitość wymiarowa jest przestrzenią topologiczną lokalnie homeomorficzną z topologiczną przestrzenią wektorową nad liczbami rzeczywistymi. Pomija to aksjomaty zbioru punktowego, dopuszczając wyższe kardynalności i nie-Hausdorffowskie rozmaitości ; i pomija wymiar skończony, umożliwiając modelowanie struktur, takich jak rozmaitości Hilberta na przestrzeniach Hilberta , rozmaitości Banacha na przestrzeniach Banacha i rozmaitości Frécheta na przestrzeniach Frécheta . Zwykle rozluźnia się jeden lub drugi warunek: rozmaitości z aksjomatami zbioru punktowego są badane w ogólnej topologii , podczas gdy rozmaitości nieskończenie wymiarowe badane są w analizie funkcjonalnej .
- Orbifoldy
- Orbifold uogólnieniem rozdzielacza pozwala na pewnego rodzaju „ osobliwości ” w topologii. Z grubsza mówiąc jest to przestrzeń, która lokalnie wygląda jak iloraz jakiejś prostej przestrzeni ( np. przestrzeni euklidesowej) przez działania różnych skończonych grup . Osobliwości odpowiadają ustalonym punktom działań grupowych, a działania muszą być w pewnym sensie kompatybilne.
- Rozmaitości i schematy algebraiczne
- Nieosobliwe rozmaitości algebraiczne nad liczbami rzeczywistymi lub zespolonymi są rozmaitościami. Uogólnia się to, po pierwsze, dopuszczając osobliwości, po drugie, dopuszczając różne pola, a po trzecie emulując łatkową konstrukcję rozmaitości: tak jak rozmaitość jest sklejana z otwartych podzbiorów przestrzeni euklidesowej, rozmaitość algebraiczna jest sklejana ze sobą z afinicznych rozmaitości algebraicznych, które są zerowymi zbiorami wielomianów nad ciałami algebraicznie domkniętymi. Schematy są również sklejane ze schematów afinicznych, które są uogólnieniem rozmaitości algebraicznych. Oba są związane z rozmaitościami, ale są konstruowane algebraicznie za pomocą snopów zamiast atlasów.
- Ze względu na pojedyncze punkty , odmiana na ogół nie jest rozmaitością, chociaż pod względem językowym francuska variété , niemiecka Mannigfaltigkeit i angielska rozmaitość są w dużej mierze synonimami . W języku francuskim rozmaitość algebraiczna nazywa się une variété algébrique ( rozmaitość algebraiczna ), natomiast rozmaitość gładka to une variété différentielle ( rozmaitość różniczkowa ).
- Przestrzeń warstwowa
- „Przestrzeń uwarstwiona” to przestrzeń, którą można podzielić na części („warstwy”), przy czym każda warstwa jest rozmaitością, z warstwami dopasowanymi do siebie w określony sposób (formalnie filtracja przez zamknięte podzbiory). Istnieją różne definicje techniczne, w szczególności uwarstwiona przestrzeń Whitneya (patrz warunki Whitneya ) dla gładkich rozmaitości i topologicznie uwarstwiona przestrzeń dla rozmaitości topologicznych. Podstawowe przykłady to rozmaitość z granicą (górna rozmaitość wymiarowa i granica miarowe 1) oraz rozmaitości z narożami (górna rozmaitość wymiarowa, granica miarowe 1, narożniki 2). Whitney stratyfikacji przestrzenie szeroka klasa miejsc, w tym algebraicznych odmian, odmian analitycznych, semialgebraic zestawów i zestawów subanalytic .
- Kompleksy CW
- CW-kompleks jest przestrzenią topologiczną utworzone przez sklejenie dyski o różnej jest łączne wymiarowości. Na ogół wynikowa przestrzeń jest pojedyncza, a więc nie jest rozmaitością. Jednak są one przedmiotem zainteresowania topologii algebraicznej, zwłaszcza teorii homotopii .
- Rozmaitości homologiczne
- Kolektora homologii jest przestrzeń, która zachowuje się jak kolektor z punktu widzenia teorii homologii. Nie są to wszystkie rozmaitości, ale (w dużym wymiarze) mogą być analizowane przez teorię chirurgiczną podobnie do rozmaitości, a niepowodzenie w byciu rozmaitością jest lokalną przeszkodą, jak w teorii chirurgii.
- Przestrzenie różniczkowe
- Niech będzie zbiorem niepustym. Załóżmy, że wybrano jakąś rodzinę funkcji rzeczywistych . Oznacz to przez . Jest to algebra ze względu na dodawanie i mnożenie przez punkt. Niech będzie wyposażony w topologię indukowaną przez . Załóżmy również, że spełnione są następujące warunki. Po pierwsze: dla każdego , gdzie i dowolnego , składu . Po drugie: każda funkcja, która w każdym punkcie lokalnie pokrywa się z jakąś funkcją z , również należy do . Para, dla której powyższe warunki są spełnione, nazywana jest przestrzenią różniczkową Sikorskiego.
Zobacz też
- Geodezyjne – najkrótsza ścieżka na zakrzywionej powierzchni lub rozmaitości riemannowskiej
- Statystyki kierunkowe : statystyki dotyczące rozmaitości
- Lista rozmaitości – artykuł z listy Wikipedii
- Oś czasu rozmaitości – Oś czasu matematyki
- Matematyka ogólnej teorii względności – Struktury i techniki matematyczne stosowane w ogólnej teorii względności
Według wymiaru
- 3-rozmaitość – przestrzeń, która lokalnie wygląda jak trójwymiarowa przestrzeń euklidesowa
- 4-rozdzielacz – Rozdzielacz o wymiarze czwartym
- 5-kolektor – Rozdzielacz o wymiarze piątym
- Rozmaitości odwzorowań
Uwagi
Bibliografia
- Freedman, Michael H. i Quinn, Frank (1990) Topology of 4-Manifolds . Wydawnictwo Uniwersytetu Princeton. ISBN 0-691-08577-3 .
- Guillemin, Victor i Pollack, Alan (1974) Topologia różnicowa . Prentice-Hall. ISBN 0-13-212605-2 . Zaawansowany tekst licencjacki / pierwszego roku magisterski inspirowany Milnorem.
- Hempel, John (1976) 3-Rozdzielacze . Wydawnictwo Uniwersytetu Princeton. ISBN 0-8218-3695-1 .
- Hirsch, Morris , (1997) Topologia różnicowa . Springer Verlag. ISBN 0-387-90148-5 . Najbardziej kompletna relacja, z historycznymi spostrzeżeniami i doskonałymi, ale trudnymi problemami. Standardowe odniesienie dla tych, którzy chcą mieć głębokie zrozumienie tematu.
- Kirby, Robion C. i Siebenmann, Laurence C. (1977) Podstawowe eseje o rozmaitościach topologicznych. Wygładzania i triangulacje . Wydawnictwo Uniwersytetu Princeton. ISBN 0-691-08190-5 . Szczegółowe studium kategorii rozmaitości topologicznych.
- Lee, John M. (2000) Wprowadzenie do rozmaitości topologicznych . Springer-Verlag. ISBN 0-387-98759-2 . Szczegółowy i wyczerpujący tekst dla absolwentów pierwszego roku.
- Lee, John M. (2003) Wprowadzenie do Smooth Manifolds . Springer-Verlag. ISBN 0-387-95495-3 . Szczegółowy i wyczerpujący tekst dla absolwentów pierwszego roku; sequel Wstępu do rozmaitości topologicznych .
- Massey, William S. (1977) Topologia algebraiczna: Wprowadzenie . Springer-Verlag. ISBN 0-387-90271-6 .
- Milnor, John (1997) Topologia z różniczkowalnego punktu widzenia . Wydawnictwo Uniwersytetu Princeton. ISBN 0-691-04833-9 . Klasyczne krótkie wprowadzenie do topologii różniczkowej.
- Munkres, James R. (1991) Analiza rozmaitości . Addison-Wesley (przedrukowane przez Westview Press) ISBN 0-201-51035-9 . Tekst licencjacki dotyczący rozmaitości w .
- Munkres, James R. (2000) Topologia . Sala Prezydencka. ISBN 0-13-181629-2 .
- Neuwirth, LP, wyd. (1975) Węzły, grupy i 3-rozmaitości. Artykuły poświęcone pamięci RH Foxa . Wydawnictwo Uniwersytetu Princeton. ISBN 978-0-691-08170-0 .
-
Riemann, Bernhard , Gesammelte mathematische Werke und wissenschaftlicher Nachlass , Sändig Reprint. ISBN 3-253-03059-8 .
- Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse. Praca doktorska z 1851 r., w którejpo raz pierwszy pojawia się„rozmaitość” ( Mannigfaltigkeit ).
- Ueber die Hypothesen, welche der Geometrie zu Grunde liegen. Wykład inauguracyjny w Getyndze z 1854 r. ( Habilitationsschrift ).
- Spivak, Michael (1965) Rachunek na rozmaitościach: nowoczesne podejście do klasycznych twierdzeń zaawansowanego rachunku różniczkowego . WA Benjamin Inc. (przedruk Addison-Wesley i Westview Press). ISBN 0-8053-9021-9 . Słynny zwięzły zaawansowany tekst na studiach licencjackich / pierwszego roku.
- Spivak, Michael (1999) A Comprehensive Introduction to Differential Geometry (3rd edition) Publish or Perish Inc. Encyklopedyczna pięciotomowa seria prezentująca na początku systematyczne traktowanie teorii rozmaitości, geometrii riemannowskiej, klasycznej geometrii różniczkowej i wielu innych tematów - oraz poziomy drugiego roku studiów magisterskich.
- Tu, Loring W. (2011). Wprowadzenie do rozmaitości (2nd ed.). Nowy Jork: Springer. Numer ISBN 978-1-4419-7399-3.. Zwięzły tekst dla absolwentów pierwszego roku.
Zewnętrzne linki
- "Rozmaitość" , Encyklopedia Matematyki , EMS Press , 2001 [1994]
- Dimensions-math.org (film wyjaśniający i wizualizujący rozmaitości aż do czwartego wymiaru.)
- Do kolektora atlas projekt Instytutu Maxa Plancka w Bonn Matematyki










![{\ Displaystyle {\ zacząć {wyrównany} T (a) & = \ chi _ {\ operatorname {prawo}} \ lewo (\ chi _ {\ operatorname {góra}} ^ {-1} \ lewo [a \ prawo] \right)\\&=\chi _{\mathrm {right} }\left(a,{\sqrt {1-a^{2}}}\right)\\&={\sqrt {1-a^ {2}}}\end{wyrównany}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40ce5573c9fdbffd539c2d9a9f80fdd33ca68ae3)


![{\ Displaystyle {\ zacząć {wyrównany} x = {\ Frac {1-s ^ {2}} {1 + s ^ {2}}} \ \ [5 pkt] y = {\ Frac {2 s} {1 + s ^{2}}}\end{wyrównany}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f08d1a41825c29ff1f55d16dae15784d549e8179)