Stała matematyczna - Mathematical constant

Stała matematyczna to liczba kluczowa, której wartość jest określona przez jednoznaczną definicję, często określaną symbolem (np. literą alfabetu ) lub imionami matematyków, aby ułatwić jej użycie w wielu problemach matematycznych . Stałe powstają w wielu dziedzinach matematyki , przy czym takie stałe jak $e$ i $π$ występują w tak różnych kontekstach, jak geometria , teoria liczb i rachunek różniczkowy .

To, co oznacza, że stała powstaje „naturalnie” i co sprawia, że stała „interesująca”, jest ostatecznie kwestią gustu, przy czym niektóre stałe matematyczne są bardziej godne uwagi z powodów historycznych niż ze względu na ich nieodłączne matematyczne zainteresowanie. Bardziej popularne stałe były badane przez wieki i obliczane z dokładnością do wielu miejsc po przecinku.

Wszystkie nazwane stałe matematyczne są liczbami definiowalnymi i zwykle są również liczbami obliczalnymi ( stała Chaitina jest znaczącym wyjątkiem).

Podstawowe stałe matematyczne

Są to stałe, z którymi można się spotkać podczas edukacji przedszkolnej w wielu krajach.

Stała Archimedesa $π$

Obwód koła o średnicy 1 wynosi

π

.

Stała $π$ (pi) ma naturalną definicję w geometrii euklidesowej jako stosunek obwodu i średnicy koła. Można go znaleźć w wielu innych miejscach w matematyce: na przykład całka Gaussa , złożone pierwiastki jedności i rozkłady Cauchy'ego w prawdopodobieństwie . Jednak jego wszechobecność nie ogranicza się do czystej matematyki. Pojawia się w wielu wzorach w fizyce, a kilka stałych fizycznych jest najbardziej naturalnie definiowanych przez $π$ lub jej odwrotność. Na przykład funkcja falowa stanu podstawowego atomu wodoru wynosi

{\ Displaystyle \ psi (\ mathbf {R} ) = {\ Frac {1} {(\ pi a_ {0} ^ {3}) ^ {1/2}}} e ^ {-r / a_ {0} },}

gdzie jest promień Bohra . $a_{0}$

$π$ jest liczbą niewymierną .

Wartość liczbowa $π$ wynosi około 3,1415926536 (sekwencja A000796 w OEIS ). Zapamiętywanie coraz bardziej dokładnych cyfr od $Õ$ jest dążenie rekord świata.

Jednostka urojona $i$

Jednostka urojona

i

na płaszczyźnie zespolonej . Liczby rzeczywiste leżą na osi poziomej, a liczby urojone leżą na osi pionowej

Urojona lub numer jednostki urojony , oznaczone jako $I$ , to matematyczny koncepcja, która rozciąga się rzeczywistą liczbę układ do liczby zespolonej układ rdzeń właściwość jednostką urojoną jest to $, że$ $2$ $= -1$ . Termin „ wyobrażony ” został ukuty, ponieważ nie ma ( rzeczywistej ) liczby mającej ujemny kwadrat . ${\ Displaystyle \ mathbb {R}}$ ${\ Displaystyle \ mathbb {C}.}$

Są to w rzeczywistości dwa złożone pierwiastki kwadratowe z -1, czyli $ja$ i $- ja$ , tak jak istnieją dwa złożone pierwiastki kwadratowe z każdej innej liczby rzeczywistej (z wyjątkiem zera , która ma jeden podwójny pierwiastek kwadratowy).

W kontekstach, w których symbol $i$ jest niejednoznaczny lub problematyczny, czasami używa się $j$ lub greckiego iota ( $ι$ ). Dotyczy to w szczególności elektrotechniki i inżynierii systemów sterowania , gdzie jednostka urojona jest często oznaczana przez $j$ , ponieważ $i$ jest powszechnie używane do oznaczania prądu elektrycznego .

liczba Eulera $e$

Wzrost wykładniczy (zielony) opisuje wiele zjawisk fizycznych.

Liczba Eulera $e$ , zwana również wykładniczą stałą wzrostu , występuje w wielu dziedzinach matematyki, a jedną z możliwych definicji jest wartość następującego wyrażenia:

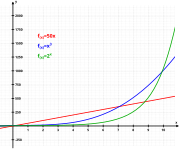
{\ Displaystyle e = \ lim _ {n \ do \ infty} \ lewo (1 + {\ Frac {1} {n}} \ po prawej) ^ {n}}

Stała $e$ jest nierozerwalnie związana z funkcją wykładniczą . ${\ Displaystyle x \ mapsto e ^ {x}}$

Szwajcarski matematyka Jacob Bernoulliego odkryto, że $e$ powstaje w związku zainteresowania : jeśli Uruchamia Konto na $ 1 i przynoszą odsetki na dorocznej wynosi $R$ , wtedy jako liczbę okresów w ciągu roku dąży do nieskończoności (sytuacja znana jako ciągłego mieszania ), przy czym ilość pieniędzy na koniec roku zbliży się do $e R$ dolarów.

Stała $e$ ma również zastosowanie w teorii prawdopodobieństwa , gdzie powstaje w sposób nie związany w oczywisty sposób ze wzrostem wykładniczym. Załóżmy na przykład, że w automacie z prawdopodobieństwem wygranej jeden do $n$ gra się $n$ razy, wtedy dla dużej liczby $n$ (np. jednego miliona) prawdopodobieństwo, że nic nie zostanie wygrane, będzie miało tendencję do $1/ e,$ ponieważ $n$ ma tendencję do nieskończoność.

Inne zastosowanie $e$ , odkryte częściowo przez Jacoba Bernoulliego wraz z francuskim matematykiem Pierre'em Raymondem de Montmort , dotyczy problemu derangements , znanego również jako problem sprawdzania kapelusza . Tutaj $n$ gości zostaje zaproszonych na przyjęcie, a przy drzwiach każdy z gości sprawdza swój kapelusz z kamerdynerem, który następnie umieszcza je w oznaczonych pudełkach. Lokaj nie zna nazwisk gości, dlatego musi ich włożyć do losowo wybranych pudełek. Problem de Montmorta polega na tym, jakie jest prawdopodobieństwo, że żaden z kapeluszy nie zostanie włożony do właściwego pudełka. Odpowiedź to

{\ Displaystyle p_ {n} = 1- {\ Frac {1} {1!}} + {\ Frac {1} {2!}} - {\ Frac {1} {3!}} + \ cdots + ( -1)^{n}{\frac {1}{n!}}}

która, gdy $n$ dąży do nieskończoności, zbliża się do $1/ e$ .

$e$ jest liczbą niewymierną .

Wartość liczbowa $e$ wynosi około 2,7182818284 (sekwencja A001113 w OEIS ).

Stała Pitagorasa $\sqrt 2$

Pierwiastek kwadratowy liczby 2 jest równa długości przeciwprostokątnej z prostokątnego trójkąta z nogami o długości 1.

Pierwiastek kwadratowy z 2 , często znany jako korzeń 2 , radykalnej 2 lub stałej Pitagorasa , jak i pisemnej $\sqrt 2$ , jest dodatnia liczba algebraiczna , że po pomnożeniu przez siebie, daje liczbę 2 . Dokładniej nazywa się ją pierwiastkiem głównym z 2 , aby odróżnić ją od liczby ujemnej o tej samej własności.

Geometrycznie pierwiastek kwadratowy z 2 jest długością przekątnej kwadratu o bokach równych jednej jednostce długości ; wynika to z twierdzenia Pitagorasa . Była to prawdopodobnie pierwsza liczba, o której wiadomo, że jest irracjonalna . Jego wartość liczbowa skrócona do 65 miejsc po przecinku to:

1.41421 35623 73095 04880 16887 24209 69807 85696 71875 37694 80731 76679 73799... (sekwencja A002193 w OEIS ).

Pierwiastek kwadratowy z 2.

Alternatywnie, szybkie przybliżenie 99/70 (≈ 1,41429) dla pierwiastka kwadratowego z dwóch było często używane przed powszechnym użyciem kalkulatorów elektronicznych i komputerów . Pomimo mianownika tylko 70, różni się od prawidłowej wartości o mniej niż 1/10 000 (ok. 7,2 × ^10-5 ).

Stała Teodora $\sqrt 3$

Wartość liczbowa $\sqrt 3$ wynosi około 1,7320508075 (sekwencja A002194 w OEIS ).

Stałe w matematyce zaawansowanej

Są to stałe często spotykane w wyższej matematyce .

Stałe Feigenbauma α i δ

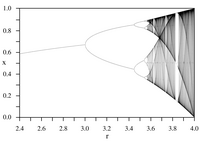
Diagram bifurkacyjny mapy logistycznej.

Iteracje map ciągłych są najprostszymi przykładami modeli układów dynamicznych . Nazwane na cześć fizyka matematycznego Mitchella Feigenbauma , dwie stałe Feigenbauma pojawiają się w takich procesach iteracyjnych: są matematycznymi niezmiennikami map logistycznych z kwadratowymi punktami maksymalnymi i ich diagramami bifurkacyjnymi .

Mapa logistyczna jest mapowaniem wielomianowym , często cytowanym jako archetypowy przykład tego, jak chaotyczne zachowanie może wynikać z bardzo prostych nieliniowych równań dynamicznych. Mapa została spopularyzowana w przełomowym artykule z 1976 roku autorstwa australijskiego biologa Roberta Maya , częściowo jako model demograficzny w czasie dyskretnym, analogiczny do równania logistycznego stworzonego po raz pierwszy przez Pierre'a François Verhulsta . Równanie różnicowe ma na celu uchwycenie dwóch skutków reprodukcji i głodu.

Wartość liczbowa α wynosi około 2,5029. Wartość liczbowa δ wynosi około 4,6692.

Stała Apéry'ego ζ(3)

Stała Aperiego jest sumą szeregu

{\ Displaystyle \ zeta (3) = 1 + {\ Frac {1} {2 ^ {3}}} + {\ Frac {1} {3 ^ {3}}} + {\ Frac {1} {4 ^ {3}}}+\cdots }

Stała Apéry'ego jest liczbą niewymierną, a jej wartość liczbowa wynosi około 1.2020569.

Pomimo tego, że specjalne wartość funkcji zeta Riemanna , stała apéry'ego powstaje naturalnie w szeregu problemów fizycznych, w tym do drugiego i trzeciego rzędu względem elektronów „S stosunek żyromagnetyczny , obliczonego przy użyciu elektrodynamiki kwantowej .

Złoty podział $φ$

Złote prostokąty w regularnym dwudziestościanie

{\ Displaystyle F_ {n} = {\ Frac {\ varphi ^ {n} - (1-\ varphi ) ^ {n}} {\ sqrt {5}}}}

Wyraźny wzór na

n-

tą liczbę Fibonacciego ze złotym podziałem

φ

.

Liczba $φ$ , zwana także złotym podziałem , często pojawia się w geometrii , szczególnie w figurach o symetrii pięciokątnej . Rzeczywiście, długość regularny pięciokąta „s Diagonal jest $cp$ razy boku. Wierzchołki dwudziestościanu foremnego to trzy wzajemnie prostopadłe złote prostokąty . Występuje również w ciągu Fibonacciego , związanym ze wzrostem przez rekurencję . Kepler udowodnił, że jest to granica stosunku kolejnych liczb Fibonacciego. Złoty podział ma najwolniejszą zbieżność spośród wszystkich niewymiernych liczb. To z tego powodu, jeden z najgorszych przypadków z aproksymacji twierdzenia Lagrange'a i jest to przypadek ekstremalny z nierównością Hurwitz dla przybliżeń diofantycznych . Być może dlatego w filotaksji (wzrost roślin) często pojawiają się kąty bliskie złotemu podziałowi . Jest w przybliżeniu równa 1,6180339887498948482, a dokładniej 2⋅sin(54°) = $\scriptstyle {\frac {1+{\sqrt {5}}}{2}}.$

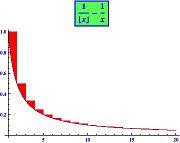
Stała Eulera-Mascheroniego γ

Obszar pomiędzy dwiema krzywymi (czerwony) dąży do granicy, a mianowicie stałej Eulera-Mascheroniego.

Stała Eulera jest zdefiniowana jako ograniczenie następujący:

{\ Displaystyle {\ zacząć {wyrównany} \ gamma & = \ lim _ {n \ do \ infty} \ lewo (\ lewo (\ suma _ {k = 1} ^ {n} {\ Frac {1} {k}) }\right)-\ln n\right)\\[5px]\end{aligned}}}

Pojawienia się symbolu stałe Eulera-Mascheroni w Mertens' trzeciego twierdzenia i relacje do funkcji gamma , z funkcją zeta i wielu całek i serii .

Nie wiadomo jeszcze, czy jest to racjonalne, czy nie. ${\ Displaystyle \ gamma}$

Wartość liczbowa wynosi około 0,57721. ${\ Displaystyle \ gamma}$

Stała Conwaya λ

{\ Displaystyle {\ zacząć {macierz} 1 \ \ 11 \ \ 21 \ \ 1211 \ \ 111221 \ \ 312211 \ \ \ vdots \ koniec {macierz}}}

Sekwencja „ patrz i mów ” Conwaya

Stała Conwaya jest niezmienną szybkością wzrostu wszystkich wyprowadzonych ciągów podobnych do sekwencji „patrz i mów” (z wyjątkiem jednego trywialnego).

Daje go unikalny dodatni pierwiastek rzeczywisty wielomianu stopnia 71 o współczynnikach całkowitych.

Wartość λ wynosi około 1,30357.

Stała Khinchina K

Jeśli liczba rzeczywista r jest zapisana jako ułamek prosty :

r=a_{0}+{\dfrac {1}{a_{1}+{\dfrac {1}{a_{2}+{\dfrac {1}{a_{3}+\cdots}} }}}},

gdzie _k są liczbami naturalnymi dla wszystkich k , a jako rosyjskiego matematyka Aleksandr Chinczyn udowodnił 1934 granica jak n dąży do nieskończoności z średniej geometrycznej ( do ₁₂ ... _n ) ^{1 /}ⁿ istnieje i jest stałą, stałą Khinchina , z wyjątkiem zestawu miary 0.

Wartość liczbowa K wynosi około 2,68545202010.

Stała Glaishera-Kinkelina A

Glaisher-Kinkelin stałe określa się jako granicę :

{\ Displaystyle A = \ lim _ {n \ rightarrow \ infty} {\ Frac {\ prod _ {k = 1} ^ {n} k ^ {k}} {n ^ {n ^ {2}/2 + n} /2+1/12}e^{-n^{2}/4}}}}

Jest to ważna stała, która pojawia się w wielu wyrażeniach dla pochodnej funkcji zeta Riemanna . Ma wartość liczbową około 1.2824271291.

Ciekawostki matematyczne i nieokreślone stałe

Prości przedstawiciele zbiorów liczb

Ta babilońska tabliczka gliniana podaje przybliżenie pierwiastka kwadratowego z 2 w czterech liczbach szesnastkowych : 1; 24, 51, 10, czyli z dokładnością do około sześciu cyfr po przecinku .

{\ Displaystyle c = \ suma _ {j = 1} ^ {\ infty} 10 ^ {-j!} = 0. \ underbrace {\ overbrace {110001} ^ {3! {\ tekst {cyfry}}} 000000000000000001} _{4!{\text{ cyfry}}}000\kropek }

Stała Liouville'a jest prostym przykładem liczby przestępnej .

Niektóre stałe, takie jak pierwiastek kwadratowy z 2 , stałym Liouville'a i Champernowne stałej :

{\ Displaystyle C_ {10} = 0. {\ kolor {niebieski} {1}} 2 {\ kolor {niebieski} {3}} 4 {\ kolor {niebieski} {5}} 6 {\ kolor {niebieski} { 7}}8{\color {blue}{9}}10{\color {blue}{11}}12{\color {blue}{13}}14{\color {blue}{15}}16\dots }

Nie są ważnymi niezmienniki matematyczne ale zachować zainteresowanie jest proste przedstawiciele specjalnych zestawów liczb, to nieracjonalne numery , że numery transcendentalne i normalne numery (w bazie 10) odpowiednio. Odkrycie liczb niewymiernych zwykle przypisuje się pitagorejskiemu Hippasosowi z Metapontum, który udowodnił, najprawdopodobniej geometrycznie, irracjonalność pierwiastka kwadratowego z 2. Stała Liouville'a, nazwana na cześć francuskiego matematyka Josepha Liouville'a , była pierwszą liczbą, która została udowodnione transcendentalne.

Stała Chaitina Ω

W informatyce podpola z algorytmicznej teorii informacji , stały Chaitin za to rzeczywista liczba reprezentująca prawdopodobieństwo , że losowo wybrana maszyna Turinga będzie halt, utworzoną z budowy z powodu Argentynie - amerykański matematyk i informatyk Grzegorz Chaitin . Stała Chaitina, chociaż nie jest obliczalna , okazała się transcendentalna i normalna . Stała Chaitina nie jest uniwersalna, w dużej mierze zależy od kodowania numerycznego używanego do maszyn Turinga; jednak jego interesujące właściwości są niezależne od kodowania.

Nieokreślone stałe

Gdy nie są określone, stałe wskazują klasy podobnych obiektów, zwykle funkcje, wszystkie równe do stałej – technicznie rzecz biorąc, można to postrzegać jako „podobieństwo do stałej”. Takie stałe pojawiają się często, gdy mamy do czynienia z całkami i równaniami różniczkowymi . Choć nieokreślone, mają określoną wartość, która często nie jest ważna.

Rozwiązania z różnymi stałymi całkowania .

{\ Displaystyle y '(x) = -2y + e ^ {-x}}

W całkach

Całki nieoznaczone nazywane są nieoznaczonymi, ponieważ ich rozwiązania są unikalne tylko do stałej. Na przykład podczas pracy nad polem liczb rzeczywistych

{\ Displaystyle \ int \ cos x \ dx = \ sin x + C}

gdzie C , stała całkowania , jest dowolną ustaloną liczbą rzeczywistą. Innymi słowy, niezależnie od wartości C , różnicowanie sin x + C względem x zawsze daje cos x .

W równaniach różniczkowych

W podobny sposób stałe pojawiają się w rozwiązaniach równań różniczkowych, w których nie podano wystarczających wartości początkowych lub warunków brzegowych . Na przykład równanie różniczkowe zwyczajne y ^' = y ( x ) ma rozwiązanie C ^{x ,} gdzie C jest dowolną stałą.

Gdy mamy do czynienia z równaniami różniczkowymi cząstkowymi , stałe mogą być funkcjami , stałymi w odniesieniu do niektórych zmiennych (ale niekoniecznie wszystkich). Na przykład PDE

{\ Displaystyle {\ Frac {\ częściowy f (x, y)} {\ częściowy x}} = 0}

ma rozwiązania f ( x , y ) = C ( y ), gdzie C ( y ) jest dowolną funkcją w zmiennej y .

Notacja

Reprezentujące stałe

Powszechnie wyraża się wartość liczbową stałej, podając jej reprezentację dziesiętną (lub tylko kilka pierwszych jej cyfr). Z dwóch powodów ta reprezentacja może powodować problemy. Po pierwsze, mimo że wszystkie liczby wymierne mają skończone lub zawsze powtarzające się rozwinięcie dziesiętne, liczby niewymierne nie mają takiego wyrażenia, które uniemożliwia ich pełne opisanie w ten sposób. Ponadto dziesiętne rozwinięcie liczby niekoniecznie jest unikatowe. Na przykład dwie reprezentacje 0,999... i 1 są równoważne w tym sensie, że reprezentują tę samą liczbę.

Obliczanie cyfr dziesiętnej ekspansji stałych było powszechnym przedsięwzięciem od wielu stuleci. Na przykład niemiecki matematyk Ludolph van Ceulen z XVI wieku spędził większą część swojego życia na obliczaniu pierwszych 35 cyfr liczby pi. Za pomocą komputerów i superkomputerów niektóre stałe matematyczne, w tym π, e i pierwiastek kwadratowy z 2, zostały obliczone na ponad sto miliardów cyfr. Opracowano szybkie algorytmy , z których niektóre — jak w przypadku stałej Apéry — są nieoczekiwanie szybkie.

{\ Displaystyle G = \ lewo. {\ zacząć {macierz} 3 \ underbrace {\ uparrow \ ldots \ uparrow} 3 \ \ \ underbrace {\ vdots} \ \ 3 \ uparrow \ uparrow \ uparrow \ uparrow 3 \ end {matrix }}\right\}{\text{64 warstwy}}}

Liczba Grahama zdefiniowana za pomocą notacji Knutha ze strzałką w górę .

Niektóre stałe różnią się tak bardzo od zwykłych, że wynaleziono nową notację, aby rozsądnie je reprezentować. Liczba Grahama ilustruje to, gdy używana jest notacja Knutha ze strzałką w górę .

Interesujące może być przedstawienie ich za pomocą ułamków ciągłych w celu wykonania różnych badań, w tym analizy statystycznej. Wiele stałych matematycznych ma postać analityczną , co oznacza, że można je skonstruować za pomocą dobrze znanych operacji, które łatwo poddają się obliczeniom. Jednak nie wszystkie stałe mają znane formy analityczne; Przykładami są stała Grossmana i stała Foiasa .

Symbolizowanie i nazywanie stałych

Symbolizowanie stałych za pomocą liter jest częstym sposobem na zwięzłość notacji . Powszechną konwencją , zapoczątkowaną przez René Descartesa w XVII wieku i Leonharda Eulera w XVIII wieku, jest używanie małych liter z początku alfabetu łacińskiego lub alfabetu greckiego w odniesieniu do stałych w ogóle. $a,b,c,\kropki$ $\alfa,\beta,\,\gamma,\kropki$

Jednak w przypadku ważniejszych stałych symbole mogą być bardziej złożone i mieć dodatkową literę, gwiazdkę , cyfrę, lemniskatę lub używać różnych alfabetów, takich jak hebrajski , cyrylica lub gotycki .

Stała Erdősa-Borweina Stała Embree'a-Trefethena Stała Bruna dla podwójnej liczby pierwszej Stałe Champernowne'a liczba kardynalna aleph naught

{\ Displaystyle E_ {B}}

{\ Displaystyle \ beta ^ {*}}

B_{2}

{\ Displaystyle C_ {b}}

\aleph_{0}

Przykłady różnych rodzajów notacji dla stałych.

Czasami symbol reprezentujący stałą to całe słowo. Na przykład 9-letni siostrzeniec amerykańskiego matematyka Edwarda Kasnera ukuł nazwy googol i googolplex .

{\ Displaystyle \ operatorname {googol} = 10 ^ {100} \, \ \ \ operatorname {googolplex} = 10 ^ {\ operatorname {googol}} = 10 ^ {10 ^ {100}}}

Inne nazwy są albo związane rozumieniu stałej ( uniwersalny paraboliczny stałej , liczby bliźniacze stałej , ...) lub do konkretnej osoby ( Stała Sierpińskiego , Josephson stałej , i tak dalej).

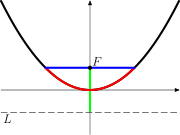
Uniwersalna stała paraboliczna jest stosunkiem, dla każdego paraboli , o długość łuku segmentu parabolicznego (czerwony), utworzonej przez latus odbytnicy (niebieski) do parametru ogniskowej (zielony).

Tabela wybranych stałych matematycznych

Użyte skróty:

R – liczba wymierna , I – liczba niewymierna (może być algebraiczna lub przestępna), A – liczba algebraiczna (nieracjonalna), T – liczba przestępna (nieracjonalna)

Gen – Ogólne , NuT – Teoria liczb , ChT – Teoria chaosu , Com – Kombinatoryka , Inf – Teoria informacji , Ana – Analiza matematyczna

Symbol	Wartość	Nazwa	Pole	n	Pierwszy opisany	Liczba znanych cyfr dziesiętnych
0	= 0	Zero	Gen	r	przez ok. 500 pne	wszystko
1	= 1	Jeden , Jedność	Gen	r		wszystko
$i$	= $\sqrt -1$	Jednostka urojona , jednostka liczba urojona	Gen , Ana	A	przez ok. 1500	wszystko
$π$	≈ 3.14159 26535 89793 23846 26433 83279 50288	Pi , Archimedes 'stała lub Ludolph ' s numer	Gen , Ana	T	przez ok. 2600 pne	62 831 853 071 796
$mi$	≈ 2.71828 18284 59045 23536 02874 71352 66249	e , stała Napiera lub liczba Eulera	Gen , Ana	T	1618	31 415 926 535 897
$\sqrt 2$	≈ 1.41421 35623 73095 04880 16887 24209 69807	Stała Pitagorasa , pierwiastek kwadratowy z 2	Gen	A	przez ok. 800 pne	10 000 000 000 000
$\sqrt 3$	≈ 1.73205 08075 68877 29352 74463 41505 87236	Stała Teodora ', pierwiastek kwadratowy z 3	Gen	A	przez ok. 800 pne	2 199 023 255 552
$\sqrt 5$	≈ 2.23606 79774 99789 69640 91736 68731 27623	pierwiastek kwadratowy z 5	Gen	A	przez ok. 800 pne	2 199 023 255 552
${\ Displaystyle \ gamma}$	≈ 0,57721 56649 01532 86060 65120 90082 40243	Stała Eulera-Mascheroni'ego	Gen , NuT		1735	600 000 000 100
$\varphi$	≈ 1.61803 39887 49894 84820 45868 34365 63811	Złoty stosunek	Gen	A	przez ok. 200 pne	10 000 000 000 000
${\ Displaystyle \ Lambda}$	${\ Displaystyle 0 \ równoważnik \ Lambda \ równoważnik 0,2}$	de Bruijn-Newman stała	Nakrętka , Ana		1950	Żaden
M ₁	≈ 0,26149 72128 47642 78375 54268 38608 69585	Stała Meissela-Mertensa	Orzech		1866 1874	8,010
${\ Displaystyle \ beta}$	≈ 0,28016 94990 23869 13303	stała Bernsteina	Ana
${\ Displaystyle \ lambda}$	≈ 0,30366 30028 98732 65859 74481 21901 55623	Stała Gaussa-Kuzmina-Wirsinga	Com		1974	385
$\sigma$	≈ 0,35323 63718 54995 98454 35165 50432 68201	Stała Hafnera-Sarnaka-McCurleya	Orzech		1993
L	≈ 0,5	Stała Landaua	Ana			1
Ω	≈ 0,56714 32904 09783 87299 99686 62210 35554	Stała Omega	Ana	T
${\ Displaystyle \ lambda}$ , ${\ Displaystyle \ mu}$	≈ 0,62432 99885 43550 87099 29363 83100 83724	Stała Golomba-Dickmana	Com , NuT		1930 1964
	≈ 0,64341 05462	Stała Cahena		T	1891	4000
C ₂	≈ 0,66016 18158 46869 57392 78121 10014 55577	Stała bliźniacza liczba pierwsza	Orzech			5020
	≈ 0,66274 34193 49181 58097 47420 97109 25290	Limit Laplace'a
${\ Displaystyle \ beta}$ ^*	≈ 0,70258	Embree-Trefethen stała	Orzech
K	≈ 0,76422 36535 89220 66299 06987 31250 09232	Stała Landaua-Ramanujana	Orzech			30,010
B ₄	≈ 0,87058 838	Stała Bruna dla czworaczków pierwszorzędnych	Orzech			8
K	≈ 0,91596 55941 77219 01505 46035 14932 38411	katalońska stała	Com			1 000 000 001 337
B' _L	= 1	Stała Legendre'a	Orzech	r		wszystko
K	≈ 1.13198 824	stała Viswanatha	Orzech			8
${\ Displaystyle \ zeta (3)}$	≈ 1.20205 69031 59594 28539 97381 61511 44999	Stała Apéry'ego		i	1979	1 200 000 000 100
${\ Displaystyle \ lambda}$	≈ 1.30357 72690 34296 39125 70991 12152 55189	Stała Conwaya	Orzech	A
$\theta$	≈ 1.30637 78838 63080 69046 86144 92602 60571	Stała Millsa	Orzech		1947	6850
${\ Displaystyle \ rho}$	≈ 1.32471 79572 44746 02596 09088 54478 09734	Stała plastyczna	Orzech	A	1928
${\ Displaystyle \ mu}$	≈ 1.45136 92348 83381 05028 39684 85892 02744	Stała Ramanujana-Soldnera	Orzech	i		75 500
	≈ 1.45607 49485 82689 67139 95953 51116 54356	Stała Backhouse'a
	≈ 1.46707 80794	Stała Portera	Orzech		1975
	≈ 1,53960 07178	Kwadratowa stała lodowa Lieba	Com	A	1967
E _B	≈ 1.60669 51524 15291 76378 33015 23190 92458	Stała Erdősa-Borweina	Orzech	i
	1.7 1,70521 11401 05367 76428 85514 53434 50816	stała Nivena	Orzech		1969
B ₂	1.90216 05831 04	Stała Brun dla bliźniaczych liczb pierwszych	Orzech		1919	12
P ₂	≈ 2,29558 71493 92638 07403 42980 49189 49039	Uniwersalna stała paraboliczna	Gen	T
${\ Displaystyle \ alfa}$	≈ 2.50290 78750 95892 82228 39028 73218 21578	Stała Feigenbauma	ChT
K	≈ 2.58498 17595 79253 21706 58935 87383 17116	Stała Sierpińskiego
	≈ 2.68545 20010 65306 44530 97148 35481 79569	Stała Chinchina	Orzech		1934	7350
F	≈ 2.80777 02420 28519 36522 15011 86557 77293	Stała Franséna-Robinsona	Ana
	≈ 3,27582 29187 21811 15978 76818 82453 84386	Stała Lévy'ego	Orzech
${\ Displaystyle \ psi}$	≈ 3.35988 56662 43177 55317 20113 02918 92717	Odwrotna stała Fibonacciego		i
${\ Displaystyle \ delta}$	≈ 4.66920 16091 02990 67185 32038 20466 20161	Stała Feigenbauma	ChT		1975

Zobacz też

Uwagi

Zewnętrzne linki

Stałe – od Wolframa MathWorld
Kalkulator odwrotny symboliczny (CECM, ISC) (mówi, jak daną liczbę można skonstruować ze stałych matematycznych)
Internetowa encyklopedia ciągów liczb całkowitych (OEIS)
Falownik Simona Plouffe'a
Strona ze stałymi matematycznymi Stevena Fincha (Zerwany link)
Steven R. Finch, „ Stałe matematyczne ”, Encyklopedia matematyki i jej zastosowań , Cambridge University Press (2003).
Strona liczb, stałych matematycznych i algorytmów Xaviera Gourdona i Pascala Sebaha

Languages

In other projects

Stała matematyczna - Mathematical constant

Zawartość

Podstawowe stałe matematyczne

Stała Archimedesa $π$

Jednostka urojona $i$

liczba Eulera $e$

Stała Pitagorasa $\sqrt 2$

Stała Teodora $\sqrt 3$

Stałe w matematyce zaawansowanej

Stałe Feigenbauma α i δ

Stała Apéry'ego ζ(3)

Złoty podział $φ$

Stała Eulera-Mascheroniego γ

Stała Conwaya λ

Stała Khinchina K

Stała Glaishera-Kinkelina A

Ciekawostki matematyczne i nieokreślone stałe

Prości przedstawiciele zbiorów liczb

Stała Chaitina Ω

Nieokreślone stałe

W całkach

W równaniach różniczkowych

Notacja

Reprezentujące stałe

Symbolizowanie i nazywanie stałych

Tabela wybranych stałych matematycznych

Zobacz też

Uwagi

Zewnętrzne linki

Languages

In other projects

Stała matematyczna - Mathematical constant

Podstawowe stałe matematyczne

Stała Archimedesa π

Jednostka urojona i

liczba Eulera e

Stała Pitagorasa √ 2

Stała Teodora √ 3

Stałe w matematyce zaawansowanej

Stałe Feigenbauma α i δ

Stała Apéry'ego ζ(3)

Złoty podział φ

Stała Eulera-Mascheroniego γ

Stała Conwaya λ

Stała Khinchina K

Stała Glaishera-Kinkelina A

Ciekawostki matematyczne i nieokreślone stałe

Prości przedstawiciele zbiorów liczb

Stała Chaitina Ω

Nieokreślone stałe

W całkach

W równaniach różniczkowych

Notacja

Reprezentujące stałe

Symbolizowanie i nazywanie stałych

Tabela wybranych stałych matematycznych

Zobacz też

Uwagi

Zewnętrzne linki

Stała Archimedesa $π$

Jednostka urojona $i$

liczba Eulera $e$

Stała Pitagorasa $\sqrt 2$

Stała Teodora $\sqrt 3$

Złoty podział $φ$