Twierdzenie o maksymalnym przepływie i przecięciu - Max-flow min-cut theorem

W informatyce i teorii optymalizacji , że maksymalna przepływu min cięcia twierdzenie stwierdza się, że w sieci przepływu , maksymalna ilość przepływającego ze strumienia źródła do zlewu jest równa całkowitej masy krawędzi w minimalnej cięcia , tzn najmniejsza całkowita waga krawędzi, których usunięcie spowodowałoby odłączenie źródła od zlewu.

Jest to szczególny przypadek twierdzenia dualności dla programów liniowych i może być wykorzystywana do wyliczania twierdzenie Mengera i twierdzenie König-Egerváry .

Definicje i stwierdzenie

Twierdzenie dotyczy dwóch wielkości: maksymalnego przepływu przez sieć i minimalnej przepustowości przekroju sieci, czyli przepustowości minimalnej osiąganej przez przepływ.

Aby sformułować twierdzenie, należy najpierw zdefiniować każdą z tych wielkości.

Niech N = ( V , E ) będzie grafem skierowanym , gdzie V oznacza zbiór wierzchołków, a E jest zbiorem krawędzi. Let s ∈ V i T ∈ V być źródłem i zlewie N , odpowiednio.

Pojemność od krawędzi jest odwzorowaniem oznaczonej przez c _UV lub C ( U , V ) w którym U , V ∈ V . Reprezentuje maksymalną ilość przepływu, która może przejść przez krawędź. ${\ Displaystyle c: E \ do \ mathbb {R} ^ {+}}$

Przepływy

Przepływu jest odwzorowaniem oznaczone lub , zgodnie z dwóch następujących ograniczeń: ${\ Displaystyle f: E \ do \ mathbb {R} ^ {+}}$${\displaystyle f_{uv}}$${\displaystyle f(u,v)}$

1. Ograniczenie pojemności : dla każdej krawędzi ,${\ Displaystyle (u, v) \ w E}$${\ Displaystyle f_ {uv} \ leq c_ {uv}.}$
2. Ochrona przepływów : Dla każdego wierzchołka oprócz i (tj. odpowiednio źródła i ujścia ) obowiązuje następująca równość:${\displaystyle v}$${\displaystyle s}$${\displaystyle t}$
   ${\ Displaystyle \ suma \ nolimits _ {\ {u: (u, v) \ w e \}} f_ {uv} = \ suma \ nolimits _ {\ {w: (v, w) \ w e \}} f_{vw}.}$

Przepływ można zwizualizować jako fizyczny przepływ płynu przez sieć, zgodnie z kierunkiem każdej krawędzi. Ograniczenie pojemności mówi wtedy, że objętość przepływająca przez każdą krawędź w jednostce czasu jest mniejsza lub równa maksymalnej pojemności krawędzi, a ograniczenie zachowania mówi, że ilość, która wpływa do każdego wierzchołka, jest równa ilości wypływającej z każdego wierzchołka, oprócz wierzchołków źródłowych i ujść.

Wartość od przepływu jest określona

${\ Displaystyle | f | = \ suma \ nolimits _ {\ {v: (s, v) \ w e \}} f_ {sv} = \ suma \ nolimits _ {\ {v: (v, t) \ w E\}}f_{vt},}$

gdzie jak powyżej jest węzłem źródłowym i jest węzłem ujścia . W analogii płynu reprezentuje ilość płynu wchodzącego do sieci w węźle źródłowym. Ze względu na aksjomat zachowania dla przepływów jest to wielkość przepływu opuszczającego sieć w węźle ujścia. ${\displaystyle s}$${\displaystyle t}$

Problem maksymalnego przepływu dotyczy największego przepływu w danej sieci.

Problem z maksymalnym przepływem. Maksymalizuj, to znaczy, aby kierować jak najwięcej przepływu zdo. ${\displaystyle |f|}$${\displaystyle s}$${\displaystyle t}$

Cięcia

Druga połowa twierdzenia o maksymalnym przepływie i przecięciu odnosi się do innego aspektu sieci: zbioru cięć. St cięcia C = ( S , T ) jest podział V tak, że s ∈ S i T ∈ T . Oznacza to, że s - t cut to podział wierzchołków sieci na dwie części, ze źródłem w jednej części i ujściem w drugiej. Zestaw cięć cięcia C to zestaw krawędzi, które łączą źródłową część cięcia z częścią zlewu: ${\ Displaystyle X_ {C}}$

${\ Displaystyle X_ {C}: = \ {(u, v) \ w e \ :\ u \ w s, v \ w t \} = (s \ razy t) \ czapka e.}$

Tak więc, jeśli wszystkie krawędzie w zbiorze cięć C zostaną usunięte, to nie jest możliwy dodatni przepływ, ponieważ w wynikowym grafie nie ma ścieżki od źródła do ujścia.

Pojemność o kroju st jest sumą pojemności krawędzi w jego wycięciu zestawie,

${\ Displaystyle c (S, T) = \ suma \ nolimity _ {(u, v) \ w X_ {C}} c_ {uv} = \ suma \ nolimity _ {(i, j) \ w E} c_ { ij}d_{ij},}$

gdzie jeśli i , inaczej. ${\displaystyle d_{ij}=1}$${\ Displaystyle i \ w S}$${\ Displaystyle j \ w T}$${\ Displaystyle 0}$

Na wykresie jest zazwyczaj wiele cięć, ale cięcia o mniejszej wadze są często trudniejsze do znalezienia.

Minimalny problem cięcia. Zminimalizuj c ( S , T ) , to znaczy określ S i T tak, aby przepustowość cięcia ST była minimalna.

Główne twierdzenie

Główne twierdzenie łączy maksymalny przepływ przez sieć z minimalnym przecięciem sieci.

Twierdzenie o minimalnym przepływie. Maksymalna wartość przepływu st jest równa minimalnej wydajności we wszystkich st cięciach.

Formułowanie programu liniowego

Problem maksymalnego przepływu i problem minimalnego cięcia można sformułować jako dwa podstawowe programy liniowe.

	Maksymalny przepływ (pierwotny)	Minimalne cięcie (podwójne)
zmienne	${\displaystyle f_{uv}}$ ${\ Displaystyle \ forall (u, v) \ w E}$ [zmienna na krawędź]	${\displaystyle d_{uv}}$ ${\ Displaystyle \ forall (u, v) \ w E}$ [zmienna na krawędź] ${\displaystyle z_{v}}$ ${\ Displaystyle \ forall v \ w V \ setminus \ {s, t \}}$ [zmienna na węzeł nieterminalny]
cel	Wyolbrzymiać ${\ Displaystyle \ suma \ nolimity _ {v: (s, v) \ w E} f_ {sv}}$ [maksymalny całkowity przepływ ze źródła]	zminimalizować ${\ Displaystyle \ suma \ nolimity _ {(u, v) \ w E} c_ {uv} d_ {uv}}$ [min całkowita pojemność krawędzi w cięciu]
ograniczenia	podlega ${\ Displaystyle {\ zacząć {wyrównany} f_ {uv} i \ leq c_ {uv} i \ forall (u, v) \ w E \ \ \ suma _ {u} f_ {uv} - \ suma _ {w} f_{vw}&=0&&v\w V\setminus \{s,t\}\end{aligned}}}$ [ograniczenie na krawędź i ograniczenie na węzeł niekońcowy]	podlega ${\ Displaystyle {\ zacząć {wyrównany} d_ {uv}-z_ {u} + z_ {v} i \ geq 0 i \ forall (u, v) \ w E, u \ neq s, v \ neq t \ \ d_ {sv}+z_{v}&\geq 1&&\forall (s,v)\in E\\d_{ut}-z_{u}&\geq 0&&\forall (u,t)\in E,u\ neq s\\\end{wyrównany}}}$ [ograniczenie na krawędź]
znak ograniczenia	${\ Displaystyle {\ zacząć {wyrównane} f_ {uv} i \ geq 0 i \ forall (u, v) \ w e \ \ \ koniec {wyrównane}}}$	${\ Displaystyle {\ zacząć {wyrównany} d_ {uv} & \ geq 0 & & \ forall (u, v) \ w e \ \ z_ {v} i \ w \ mathbb {R} i \ forall v \ w V \ setminus \{s,t\}\end{wyrównany}}}$

Max-flow LP jest prosty. Podwójny LP uzyskuje się za pomocą algorytmu opisanego w dualnym programie liniowym . Powstały LP wymaga pewnego wyjaśnienia. Interpretacja zmiennych w min-cut LP to:

${\ Displaystyle d_ {uv} = {\ zacząć {przypadki} 1, & {\ tekst {jeśli}} u \ w S {\ tekst { i}} v \ w T {\ tekst { (krawędź}} uv { \text{ jest w cięciu) }}\\0,&{\text{otherwise}}\end{cases}}}$

${\ Displaystyle Z_ {u} = {\ zacząć {przypadki} 1 i {\ tekst {jeśli}} u \ w S \ \ 0 i {\ tekst {inaczej}} \ koniec {przypadki}}}$

Cel minimalizacji sumuje pojemność na wszystkich krawędziach, które są zawarte w cięciu.

Ograniczenia gwarantują, że zmienne rzeczywiście reprezentują legalny krój:

• Ograniczenia (odpowiednik ) gwarantują, że dla węzłów niekońcowych u,v , jeśli u jest w S , a v jest w T , to krawędź ( u , v ) jest liczona w przekroju ( ).${\ Displaystyle d_ {uv}-z_ {u} + z_ {v} \ geq 0}$${\displaystyle d_{uv}\geq z_{u}-z_{v}}$${\displaystyle d_{uv}\geq 1}$
• Ograniczenia (odpowiednik ) gwarantują, że jeśli v jest w T , to krawędź (s,v) jest liczona w cięciu (ponieważ s jest z definicji w S ).${\displaystyle d_{sv}+z_{v}\geq 1}$${\displaystyle d_{sv}\geq 1-z_{v}}$
• Ograniczenia (równoważne z ) gwarantują, że jeśli u jest w S , to krawędź (u,t) jest liczona w przekroju (ponieważ t jest z definicji w T ).${\ Displaystyle d_ {ut}-z_ {u} \ geq 0}$${\displaystyle d_{ut}\geq z_{u}}$

Zauważ, że ponieważ jest to problem minimalizacji, nie musimy gwarantować, że krawędzi nie ma w cięciu - musimy tylko zagwarantować, że każda krawędź, która powinna być w cięciu, jest sumowana w funkcji celu.

Równość w twierdzeniu max-flow min-cut wynika z twierdzenia o silnej dualności w programowaniu liniowym , które mówi, że jeśli program pierwotny ma rozwiązanie optymalne x *, to program dualny również ma rozwiązanie optymalne y *, takie że optymalne wartości utworzone przez te dwa rozwiązania są równe.

Przykład

Liczba po prawej to sieć o wartości przepływu 7. Adnotacja numeryczna na każdej strzałce, w postaci x / y , wskazuje przepływ ( x ) i pojemność ( y ). Strumienie wychodzące ze źródła to siedem (4+3=7), podobnie jak strumienie do zlewu (3+4=7).

Wierzchołek w kolorze białym i wierzchołki w kolorze szarym tworzą podzbiory S i T cięcia st, którego zestaw cięcia zawiera przerywane krawędzie. Ponieważ przepustowość odcinka wynosi 7, co jest równe wartości przepływu, twierdzenie max-flow min-cut wskazuje, że zarówno wartość przepływu jak i przepustowość odcinka są optymalne w tej sieci.

Zwróć uwagę, że przepływ przez każdą z przerywanych krawędzi jest na pełnych obrotach: jest to „wąskie gardło” systemu. Natomiast w prawej części sieci dostępne są wolne moce produkcyjne. W szczególności przepływ z węzła pierwszego do węzła drugiego nie musi być równy 1. Gdyby nie było przepływu między węzłem pierwszym i drugim, wówczas dane wejściowe do ujścia zmieniłyby się na 4/4 i 3/5; całkowity przepływ nadal będzie wynosił siedem (4+3=7). Z drugiej strony, jeśli przepływ z węzła pierwszego do węzła drugiego zostanie podwojony do 2, wówczas dane wejściowe do ujścia zmienią się na 2/4 i 5/5; całkowity przepływ ponownie pozostałby na poziomie siedmiu (2+5=7).

Podanie

Twierdzenie Cederbauma o maksymalnym przepływie

Problem maksymalnego przepływu można sformułować jako maksymalizację prądu elektrycznego przez sieć złożoną z nieliniowych elementów rezystancyjnych. W tym preparacie, graniczną prądu I _w pomiędzy zaciskami wejściowymi sieci elektrycznej, gdy napięcie wejściowe V _z podejść jest równa masie cięcia ustalone minimalne wagi.   ${\displaystyle \infty}$

${\ Displaystyle \ lim _ {V_ {\ tekst {w}} \ do \ infty} (I_ {w}) = \ min _ {X_ {C}} \ suma _ {(U, V) \ w X_ {C }}c_{uv}}$

Uogólnione twierdzenie o minimalnym przecięciu maksymalnego przepływu

Oprócz pojemności krawędzi, rozważmy, że w każdym wierzchołku istnieje pojemność, to znaczy odwzorowanie oznaczone przez c ( v ) , takie, że przepływ f musi spełniać nie tylko ograniczenie pojemności i zachowanie przepływów, ale także pojemność wierzchołków ograniczenie ${\ Displaystyle c: V \ do \ mathbb {R} ^ {+}}$  

${\ Displaystyle \ forall v \ w V \ setminus \ {s, t \}: \ qquad \ suma \ nolimity _ {\ {u \ w V \ mid (u, v) \ w e \}} f_ {uv} \leq c(v).}$

Innymi słowy, wielkość przepływu przechodzącego przez wierzchołek nie może przekroczyć jego przepustowości. Zdefiniuj cięcie st jako zestaw wierzchołków i krawędzi, tak aby dla każdej ścieżki od s do t ścieżka zawierała element cięcia. W tym przypadku pojemność cięcia jest sumą pojemności każdej krawędzi i wierzchołka w niej.

W tej nowej definicji uogólnione twierdzenie o maksymalnym przepływie min-cut stwierdza, że ​​maksymalna wartość przepływu st jest równa minimalnej przepustowości st cut w nowym sensie.

Twierdzenie Mengera

W zagadnieniu nieskierowanych rozłącznych krawędzi otrzymujemy graf nieskierowany G = ( V , E ) oraz dwa wierzchołki s i t , i musimy znaleźć maksymalną liczbę rozłącznych krawędzi st w G .

Twierdzenie Mengera mówi, że maksymalna liczba rozłącznych krawędzi ścieżek w grafie nieskierowanym jest równa minimalnej liczbie krawędzi w st cut-set.

Problem wyboru projektu

W zadaniu wyboru projektów występuje n projektów i m maszyn. Każdy projekt p _ja daje przychodów r ( p _I ) i każda maszyna q _j Koszty c ( q _j ) do zakupu. Każdy projekt wymaga kilku maszyn, a każda maszyna może być współdzielona przez kilka projektów. Problem polega na ustaleniu, które projekty i maszyny należy odpowiednio wybrać i kupić, aby zysk był zmaksymalizowany.

Niech P będzie zbiorem projektów nie wybranych i P będzie zbiorem maszyn zakupione, to problem można sformułować,

${\ Displaystyle \ max \ {g \} = \ suma _ {i} r (p_ {i}) - \ suma _ {p_ {i} \ w P} r (p_ {i}) - \ suma _ {q_ {j}\w Q}c(q_{j}).}$

Ponieważ pierwszy wyraz nie zależy od wyboru P i Q , ten problem maksymalizacji można zamiast tego sformułować jako problem minimalizacji, to znaczy

${\ Displaystyle \ min \ {g' \} = \ suma _ {p_ {i} \ w P} r (p_ {i}) + \ suma _ {q_ {j} \ w Q} c (q_ {j} ).}$

Powyższy problem minimalizacji można zatem sformułować jako problem minimalnego cięcia, konstruując sieć, w której źródło jest połączone z projektami o pojemności r ( p _i ) , a zlew przez maszyny o pojemności c ( q _j ) . Krawędź ( s _I , Q _j ) o nieskończonej pojemności jest dodawane, jeśli projekt P _i wymaga urządzenia q _j . St cut-zestaw przedstawia projekty i maszyn w P i Q odpowiednio. Za pomocą twierdzenia o maksymalnym przepływie można rozwiązać problem jako problem maksymalnego przepływu .

Rysunek po prawej przedstawia sformułowanie sieciowe następującego problemu wyboru projektów:

	Projekt r ( p i )	Maszyna c ( q j )
1	100	200	Projekt 1 wymaga maszyn 1 i 2.
2	200	100	Projekt 2 wymaga maszyny 2.
3	150	50	Projekt 3 wymaga maszyny 3.

Minimalna wydajność cięcia to 250, a suma przychodów z każdego projektu to 450; zatem maksymalny zysk g wynosi 450 − 250 = 200, wybierając projekty p ₂ i p ₃ .

Pomysł polega na tym, aby „przepłynąć” zyski z każdego projektu przez „rury” jego maszyn. Jeśli nie możemy napełnić rury z maszyny, zwrot maszyny jest mniejszy niż jej koszt, a algorytm minimalnego cięcia uzna, że ​​taniej będzie odciąć krawędź zysku projektu, a nie krawędź kosztu maszyny.

Problem z segmentacją obrazu

W problemie segmentacji obrazu występuje n pikseli. Każdy piksel i może być przypisana wartość pierwszoplanowy  f _I lub wartość tła b _I . Jest kara p _ij jeśli pikseli I, J sąsiadują i mają różne zadania. Problem polega na przypisaniu pikseli do pierwszego planu lub tła tak, aby suma ich wartości minus kary była maksymalna.

Niech P będzie zbiorem pikseli przypisanych do pierwszego planu, a Q będzie zbiorem punktów przypisanych do tła, to problem można sformułować jako:

${\ Displaystyle \ max \ {g \} = \ suma _ {i \ w P} f_ {i} + \ suma _ {i \ w Q} b_ {i} - \ suma _ {i \ w P, j \ w Q\lor j\in P,i\in Q}p_{ij}.}$

Ten problem maksymalizacji można zamiast tego sformułować jako problem minimalizacji, to znaczy

${\ Displaystyle \ min \ {g' \} = \ suma _ {i \ w p, j \ w Q \ lub j \ w p, i \ w Q} p_ {ij}.}$

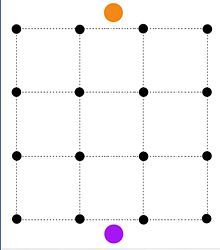
Powyższy problem minimalizacji może być formułowany w postaci problemu minimalnej zmniejszono o budowie sieci, w którym źródło (pomarańczowy węzła) jest podłączony do wszystkich pikseli o pojemności  f _I oraz umywalka (lila węzła) jest połączony wszystkich pikseli o pojemności b _ja . Dwie krawędzie ( I, J ) i ( J, I ) z p _ij pojemności dodaje dwóch sąsiednich pikseli. Pierwszy zestaw cięć reprezentuje następnie piksele przypisane do pierwszego planu w P i piksele przypisane do tła w Q .

Historia

Relację z odkrycia twierdzenia podali Ford i Fulkerson w 1962 roku:

„Określenie maksymalnego przepływu w stanie ustalonym z jednego punktu do drugiego w sieci podlegającej ograniczeniom przepustowości na łukach… zostało postawione autorom wiosną 1955 roku przez TE Harrisa, który we współpracy z generałem FS Rossem (w stanie spoczynku) sformułował uproszczony model przepływu ruchu kolejowego i wskazał ten konkretny problem jako główny sugerowany przez model.Niedługo po tym pojawił się główny wynik, Twierdzenie 5.1, które nazywamy twierdzeniem o maksymalnym przepływie, został domyślony i ustalony. Od tego czasu pojawiło się wiele dowodów."

Dowód

Niech G = ( V , E ) są skierowane do sieci (wykres) z s i t są źródła i zlewie G , odpowiednio.

Rozważmy przepływu F obliczane dla G przez algorytm Ford-Fulkersona . Na wykresie reszt ( G _f  ) otrzymanym dla G (po ostatecznym przypisaniu przepływu przez algorytm Forda-Fulkersona ), zdefiniuj dwa podzbiory wierzchołków w następujący sposób:   

1. A : zbiór wierzchołków osiągalnych z s w G _f
2. A ^c : zbiór pozostałych wierzchołków tj. V − A

Prawo. Wartość (  C  ) = C ( , ^C ) , przy czym pojemność o cięcia st jest określona

${\ Displaystyle c (S, T) = \ suma \ nolimity _ {(u, v) \ w S \ razy T} c_ {uv}}$.

Teraz wiemy, dla każdego podzbioru wierzchołków A . Dlatego dla value(  f  ) = c ( A , A ^c ) potrzebujemy: ${\ Displaystyle wartość (f) = f_ {out} (A)-f_ {w} (A)}$

• Wszystkie krawędzie wychodzące z cięcia muszą być w pełni nasycone .
• Wszystkie krawędzie przychodzące do cięcia muszą mieć zerowy przepływ .

Aby udowodnić powyższe twierdzenie, rozważamy dwa przypadki:

• W G istnieje krawędź wychodząca taka, że ​​nie jest nasycona, tj. f  ( x , y ) < c _xy . Oznacza to, że istnieje przednia krawędź od x do y w G _f , a zatem istnieje droga od s do y w G _f , co jest sprzecznością. Stąd każda krawędź wychodząca ( x , y ) jest w pełni nasycona.${\ Displaystyle (x, y), x \ w A, y \ w A ^ {c}}$ 

• W G istnieje nadchodzące zbocze , które przenosi pewien niezerowy przepływ, tj. f  ( y , x ) > 0 . Oznacza to, że istnieje wsteczna krawędź od x do y w G _f , a zatem istnieje ścieżka od s do y w G _f , co jest znowu sprzecznością. Stąd każda przychodząca krawędź ( y , x ) musi mieć zerowy przepływ.${\ Displaystyle (y, x), x \ w A, y \ w A ^ {c}}$ 

Oba powyższe stwierdzenia dowodzą, że przepustowość przerobu uzyskana w opisany sposób jest równa przepływowi uzyskanemu w sieci. Również przepływ został uzyskany przez algorytm Forda-Fulkersona , więc jest to również maksymalny przepływ sieci.

Ponadto, ponieważ każdy przepływ w sieci jest zawsze mniejszy lub równy przepustowości każdego możliwego cięcia w sieci, wyżej opisane odcięcie jest również odcięciem minimalnym, które uzyskuje przepływ maksymalny .

Następstwem tego dowodu jest to, że maksymalny przepływ przez dowolny zbiór krawędzi w przekroju grafu jest równy minimalnej przepustowości wszystkich poprzednich cięć.

Zobacz też

• Przypuszczenie GNRS
• Programowanie liniowe
• Maksymalny przepływ
• Minimalne cięcie
• Sieć przepływu
• Algorytm Edmondsa-Karpa
• Algorytm Forda-Fulkersona
• Przybliżone twierdzenie o minimalnym przepływie przy maksymalnym przepływie
• Twierdzenie Mengera

Bibliografia

• Eugene Lawler (2001). „4.5. Kombinatoryczne implikacje twierdzenia o maksymalnym przepływie i przecięciu, 4.6. Interpretacja programowania liniowego twierdzenia o maksymalnym przepływie i przecięciu”. Optymalizacja kombinatoryczna: sieci i Matroidy . Dover. s. 117–120. Numer ISBN 0-486-41453-1.
• Christos H. Papadimitriou , Kenneth Steiglitz (1998). „6.1 Twierdzenie o maksymalnym przepływie i przecięciu”. Optymalizacja kombinatoryczna: algorytmy i złożoność . Dover. s. 120–128. Numer ISBN 0-486-40258-4.
• Vijay V. Vazirani (2004). „12. Wprowadzenie do LP-Dualności”. Algorytmy aproksymacyjne . Skoczek. s. 93–100. Numer ISBN 3-540-65367-8.