Jeden siódmy obszar trójkąta - One-seventh area triangle
W geometrii płaskiej , trójkąta ABC zawiera trójkąt o jedną siódmą obszarze od ABC , który jest wykonany w następujący sposób: boki trójkąta leżą na cevians P, Q, R , w którym
- p łączy A z punktem na BC, który jest jedną trzecią odległości od B do C ,
- q łączy B z punktem na CA znajdującym się w jednej trzeciej odległości od C do A ,
- r łączy C z punktem na AB, który jest jedną trzecią odległości od A do B .
Dowód istnienia trójkąta o powierzchni jednej siódmej wynika z konstrukcji sześciu równoległych linii:
- dwa równoległe do p , jeden do C , drugi do qr
- dwa równoległe do q , jeden do A , drugi do rp
- dwa równoległe do r , jeden do B , drugi do pq .
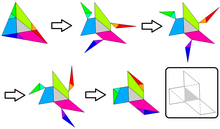
Sugestia Hugo Steinhausa jest taka, aby trójkąt (środkowy) o bokach p,q,r odbijał się w jego bokach i wierzchołkach. Te sześć dodatkowych trójkątów częściowo pokrywa ABC i pozostawia sześć wystających dodatkowych trójkątów leżących poza ABC . Skupiając się na równoległości pełnej konstrukcji (oferowanej przez Martina Gardnera za pośrednictwem internetowego magazynu Jamesa Randiego ), oczywiste są parami kongruencje nawisających i brakujących fragmentów ABC . Jak widać w rozwiązaniu graficznym, sześć plus oryginał równa się całemu trójkątowi ABC .
Wczesny pokaz tej konstrukcji geometrycznej i obliczania pola został przedstawiony przez Roberta Pottsa w 1859 roku w swoim podręczniku geometrii euklidesowej.
Według Cooka i Wooda (2004) ten trójkąt zadziwił Richarda Feynmana podczas rozmowy przy obiedzie; podają cztery różne dowody.
Bardziej ogólny wynik jest znany jako twierdzenie Routha .
Bibliografia
- HSM Coxeter (1969) Wprowadzenie do geometrii , strona 211, John Wiley & Sons .