Radialna sieć funkcji bazowej - Radial basis function network

W dziedzinie modelowania matematycznego sieć radialnych funkcji bazowych jest sztuczną siecią neuronową, która wykorzystuje radialne funkcje bazowe jako funkcje aktywacji . Wyjście sieci jest liniową kombinacją radialnych funkcji bazowych wejść i parametrów neuronu. Sieci funkcji radialnych mają wiele zastosowań, w tym aproksymację funkcji , przewidywanie szeregów czasowych , klasyfikację i sterowanie systemem . Zostały one po raz pierwszy sformułowane w pracy z 1988 roku przez Broomheada i Lowe'a, badaczy z Royal Signals and Radar Establishment .

Architektura sieci

Architektura radialnej sieci funkcji bazowych. Wektor wejściowy jest używany jako dane wejściowe do wszystkich radialnych funkcji bazowych, z których każda ma inne parametry. Wyjście sieci jest liniową kombinacją wyjść z radialnych funkcji bazowych.${\displaystyle x}$

Sieci z promieniową funkcją bazową (RBF) zazwyczaj mają trzy warstwy: warstwę wejściową, warstwę ukrytą z nieliniową funkcją aktywacji RBF i liniową warstwę wyjściową. Wejście można zamodelować jako wektor liczb rzeczywistych . Wynikiem sieci jest wtedy funkcja skalarna wektora wejściowego , i jest dana wzorem ${\displaystyle \mathbf {x} \in \mathbb {R} ^{n}}$${\displaystyle \varphi :\mathbb {R} ^{n}\to \mathbb {R} }$

${\displaystyle \varphi (\mathbf {x} )=\sum _{i=1}^{N}a_{i}\rho (||\mathbf {x} -\mathbf {c} _{i}||)}$

gdzie jest liczbą neuronów w warstwie ukrytej, jest wektorem środkowym dla neuronu i jest wagą neuronu w neuronie z wyjściem liniowym. Funkcje zależne tylko od odległości od wektora środkowego są promieniowo symetryczne względem tego wektora, stąd nazwa radialna funkcja bazowa. W podstawowej formie wszystkie wejścia są połączone z każdym ukrytym neuronem. Za normę zwykle przyjmuje się odległość euklidesową (chociaż odległość Mahalanobisa wydaje się działać lepiej z rozpoznawaniem wzorców), a promieniowa funkcja bazowa jest powszechnie uważana za Gaussa${\displaystyle N}$${\displaystyle \mathbf {c} _{i}}$${\displaystyle i}$${\displaystyle a_{i}}$${\displaystyle i}$

${\displaystyle \rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}=\exp \left[-\beta _{i}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert ^{2}\right]}$.

Funkcje bazowe Gaussa są lokalne względem wektora środkowego w tym sensie, że

${\displaystyle \lim _{||x||\to \infty }\rho (\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert )=0}$

tzn. zmiana parametrów jednego neuronu ma niewielki wpływ na wartości wejściowe, które są daleko od centrum tego neuronu.

Biorąc pod uwagę pewne łagodne warunki dotyczące kształtu funkcji aktywacji, sieci RBF są uniwersalnymi aproksymatorami na zwartym podzbiorze . Oznacza to, że sieć RBF z wystarczającą liczbą ukrytych neuronów może aproksymować dowolną ciągłą funkcję na zamkniętym, ograniczonym zbiorze z dowolną precyzją. ${\displaystyle \mathbb {R} ^{n}}$

Parametry , i są określane w sposób, który optymalizuje dopasowanie danych do danych. ${\displaystyle a_{i}}$${\displaystyle \mathbf {c} _{i}}$${\displaystyle \beta _{i}}$${\displaystyle \varphi }$

Dwie nieznormalizowane promieniowe funkcje bazowe w jednym wymiarze wejściowym. Podstawowe centra funkcyjne znajdują się pod adresem i .${\displaystyle c_{1}=0.75}$${\displaystyle c_{2}=3.25}$

Znormalizowane

Dwie znormalizowane promieniowe funkcje bazowe w jednym wymiarze wejściowym ( sigmoidy ). Podstawowe centra funkcyjne znajdują się pod adresem i .${\displaystyle c_{1}=0.75}$${\displaystyle c_{2}=3.25}$

Trzy znormalizowane promieniowe funkcje bazowe w jednym wymiarze wejściowym. Dodatkowa funkcja podstawowa ma centrum na${\displaystyle c_{3}=2.75}$

Cztery znormalizowane promieniowe funkcje bazowe w jednym wymiarze wejściowym. Czwarta funkcja bazowa ma centrum w . Zauważ, że pierwsza funkcja bazowa (kolor ciemnoniebieski) została zlokalizowana.${\displaystyle c_{4}=0}$

Znormalizowana architektura

Oprócz powyższej nieznormalizowanej architektury, sieci RBF mogą być znormalizowane . W tym przypadku mapowanie to

${\displaystyle \varphi (\mathbf {x} )\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\sum _{i=1}^{N}a_{i}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}{\sum _{i=1}^{N}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}}=\sum _{i=1}^{N}a_{i}u{\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}$

gdzie

${\displaystyle u{\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}{\sum _{j=1}^{N}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{j}\right\Vert {\big )}}}}$

jest znana jako znormalizowana radialna funkcja bazowa .

Teoretyczna motywacja do normalizacji

Istnieje teoretyczne uzasadnienie takiej architektury w przypadku stochastycznego przepływu danych. Załóż stochastyczne przybliżenie jądra dla łącznej gęstości prawdopodobieństwa

${\displaystyle P\left(\mathbf {x} \land y\right)={1 \over N}\sum _{i=1}^{N}\,\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}\,\sigma {\big (}\left\vert y-e_{i}\right\vert {\big )}}$

gdzie wagi i są przykładami z danych i wymagamy normalizacji jąder ${\displaystyle \mathbf {c} _{i}}$${\displaystyle e_{i}}$

${\displaystyle \int \rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}\,d^{n}\mathbf {x} =1}$

i

${\displaystyle \int \sigma {\big (}\left\vert y-e_{i}\right\vert {\big )}\,dy=1}$.

Gęstości prawdopodobieństwa w przestrzeniach wejściowych i wyjściowych wynoszą

${\displaystyle P\left(\mathbf {x} \right)=\int P\left(\mathbf {x} \land y\right)\,dy={1 \over N}\sum _{i=1}^{N}\,\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}$

i

Oczekiwanie y dla danych wejściowych to ${\displaystyle \mathbf {x} }$

${\displaystyle \varphi \left(\mathbf {x} \right)\ {\stackrel {\mathrm {def} }{=}}\ E\left(y\mid \mathbf {x} \right)=\int y\,P\left(y\mid \mathbf {x} \right)dy}$

gdzie

${\displaystyle P\left(y\mid \mathbf {x} \right)}$

jest prawdopodobieństwem warunkowym danego y . Prawdopodobieństwo warunkowe jest powiązane z prawdopodobieństwem łącznym za pomocą twierdzenia Bayesa${\displaystyle \mathbf {x} }$

${\displaystyle P\left(y\mid \mathbf {x} \right)={\frac {P\left(\mathbf {x} \land y\right)}{P\left(\mathbf {x} \right)}}}$

co daje

${\displaystyle \varphi \left(\mathbf {x} \right)=\int y\,{\frac {P\left(\mathbf {x} \land y\right)}{P\left(\mathbf {x} \right)}}\,dy}$.

To staje się

${\displaystyle \varphi \left(\mathbf {x} \right)={\frac {\sum _{i=1}^{N}e_{i}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}{\sum _{i=1}^{N}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}}=\sum _{i=1}^{N}e_{i}u{\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}$

kiedy wykonywane są integracje.

Lokalne modele liniowe

Czasami wygodnie jest rozszerzyć architekturę o lokalne modele liniowe . W takim przypadku architektury stają się, w pierwszej kolejności,

${\displaystyle \varphi \left(\mathbf {x} \right)=\sum _{i=1}^{N}\left(a_{i}+\mathbf {b} _{i}\cdot \left(\mathbf {x} -\mathbf {c} _{i}\right)\right)\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}$

i

${\displaystyle \varphi \left(\mathbf {x} \right)=\sum _{i=1}^{N}\left(a_{i}+\mathbf {b} _{i}\cdot \left(\mathbf {x} -\mathbf {c} _{i}\right)\right)u{\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}$

odpowiednio w przypadkach nieznormalizowanych i znormalizowanych. Oto wagi do ustalenia. Możliwe są również terminy liniowe wyższego rzędu. ${\displaystyle \mathbf {b} _{i}}$

Ten wynik można zapisać

${\displaystyle \varphi \left(\mathbf {x} \right)=\sum _{i=1}^{2N}\sum _{j=1}^{n}e_{ij}v_{ij}{\big (}\mathbf {x} -\mathbf {c} _{i}{\big )}}$

gdzie

${\displaystyle e_{ij}={\begin{cases}a_{i},&{\mbox{if }}i\in [1,N]\\b_{ij},&{\mbox{if }}i\in [N+1,2N]\end{cases}}}$

i

${\displaystyle v_{ij}{\big (}\mathbf {x} -\mathbf {c} _{i}{\big )}\ {\stackrel {\mathrm {def} }{=}}\ {\begin{cases}\delta _{ij}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )},&{\mbox{if }}i\in [1,N]\\\left(x_{ij}-c_{ij}\right)\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )},&{\mbox{if }}i\in [N+1,2N]\end{cases}}}$

w przypadku nieznormalizowanym i

${\displaystyle v_{ij}{\big (}\mathbf {x} -\mathbf {c} _{i}{\big )}\ {\stackrel {\mathrm {def} }{=}}\ {\begin{cases}\delta _{ij}u{\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )},&{\mbox{if }}i\in [1,N]\\\left(x_{ij}-c_{ij}\right)u{\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )},&{\mbox{if }}i\in [N+1,2N]\end{cases}}}$

w znormalizowanym przypadku.

Tutaj jest funkcją Kronecker delta określa się jako ${\displaystyle \delta _{ij}}$

${\displaystyle \delta _{ij}={\begin{cases}1,&{\mbox{if }}i=j\\0,&{\mbox{if }}i\neq j\end{cases}}}$.

Trening

Sieci RBF są zazwyczaj trenowane z par wartości wejściowych i docelowych , za pomocą dwuetapowego algorytmu. ${\displaystyle \mathbf {x} (t),y(t)}$${\displaystyle t=1,\dots ,T}$

W pierwszym kroku wybierane są środkowe wektory funkcji RBF w warstwie ukrytej. Ten krok można wykonać na kilka sposobów; centra mogą być losowo wybrane z pewnego zestawu przykładów lub można je określić za pomocą grupowania k-średnich . Zauważ, że ten krok nie jest nadzorowany . ${\displaystyle \mathbf {c} _{i}}$

Drugi krok po prostu dopasowuje model liniowy ze współczynnikami do wyników ukrytej warstwy w odniesieniu do jakiejś funkcji celu. Wspólną funkcją celu, przynajmniej dla estymacji regresji/funkcji, jest funkcja najmniejszych kwadratów: ${\displaystyle w_{i}}$

${\displaystyle K(\mathbf {w} )\ {\stackrel {\mathrm {def} }{=}}\ \sum _{t=1}^{T}K_{t}(\mathbf {w} )}$

gdzie

${\displaystyle K_{t}(\mathbf {w} )\ {\stackrel {\mathrm {def} }{=}}\ {\big [}y(t)-\varphi {\big (}\mathbf {x} (t),\mathbf {w} {\big )}{\big ]}^{2}}$.

Wyraźnie uwzględniliśmy zależność od wag. Minimalizacja funkcji celu najmniejszych kwadratów poprzez optymalny dobór wag optymalizuje dokładność dopasowania.

Są sytuacje, w których należy zoptymalizować wiele celów, takich jak płynność i dokładność. W takim przypadku warto zoptymalizować uregulowaną funkcję celu, taką jak

${\displaystyle H(\mathbf {w} )\ {\stackrel {\mathrm {def} }{=}}\ K(\mathbf {w} )+\lambda S(\mathbf {w} )\ {\stackrel {\mathrm {def} }{=}}\ \sum _{t=1}^{T}H_{t}(\mathbf {w} )}$

gdzie

${\displaystyle S(\mathbf {w} )\ {\stackrel {\mathrm {def} }{=}}\ \sum _{t=1}^{T}S_{t}(\mathbf {w} )}$

i

${\displaystyle H_{t}(\mathbf {w} )\ {\stackrel {\mathrm {def} }{=}}\ K_{t}(\mathbf {w} )+\lambda S_{t}(\mathbf {w} )}$

gdzie optymalizacja S maksymalizuje gładkość i jest znana jako parametr regularyzacji . ${\displaystyle \lambda }$

Trzeci opcjonalny krok wstecznej propagacji może być wykonany w celu dokładnego dostrojenia wszystkich parametrów sieci RBF.

Interpolacja

Sieci RBF mogą być użyte do interpolacji funkcji, gdy wartości tej funkcji są znane na skończonej liczbie punktów: . Biorąc znane punkty jako środki radialnych funkcji bazowych i obliczając wartości funkcji bazowych w tych samych punktach wagi można rozwiązać z równania ${\displaystyle y:\mathbb {R} ^{n}\to \mathbb {R} }$${\displaystyle y(\mathbf {x} _{i})=b_{i},i=1,\ldots ,N}$${\displaystyle \mathbf {x} _{i}}$${\displaystyle g_{ij}=\rho (||\mathbf {x} _{j}-\mathbf {x} _{i}||)}$

${\displaystyle \left[{\begin{matrix}g_{11}&g_{12}&\cdots &g_{1N}\\g_{21}&g_{22}&\cdots &g_{2N}\\\vdots &&\ddots &\vdots \\g_{N1}&g_{N2}&\cdots &g_{NN}\end{matrix}}\right]\left[{\begin{matrix}w_{1}\\w_{2}\\\vdots \\w_{N}\end{matrix}}\right]=\left[{\begin{matrix}b_{1}\\b_{2}\\\vdots \\b_{N}\end{matrix}}\right]}$

Można wykazać, że macierz interpolacji w powyższym równaniu jest nieosobliwa, jeśli punkty są różne, a zatem wagi można rozwiązać za pomocą prostej algebry liniowej: ${\displaystyle \mathbf {x} _{i}}$${\displaystyle w}$

${\displaystyle \mathbf {w} =\mathbf {G} ^{-1}\mathbf {b} }$

gdzie . ${\displaystyle G=(g_{ij})}$

Przybliżenie funkcji

Jeśli celem nie jest wykonanie ścisłej interpolacji, ale bardziej ogólne przybliżenie funkcji lub klasyfikacja, optymalizacja jest nieco bardziej złożona, ponieważ nie ma oczywistego wyboru dla centrów. Trening odbywa się zazwyczaj w dwóch fazach, najpierw ustalając szerokość i środki, a następnie ciężary. Można to uzasadnić, biorąc pod uwagę różną naturę nieliniowych ukrytych neuronów w porównaniu z liniowym neuronem wyjściowym.

Szkolenie podstawowych ośrodków funkcyjnych

Centra funkcji bazowych mogą być losowo próbkowane spośród wystąpień wejściowych lub uzyskane za pomocą algorytmu uczenia ortogonalnego najmniejszych kwadratów lub znalezione przez grupowanie próbek i wybieranie średnich skupień jako centrów.

Szerokości RBF są zwykle ustawione na taką samą wartość, która jest proporcjonalna do maksymalnej odległości między wybranymi środkami.

Pseudoodwrotne rozwiązanie dla wag liniowych

Po ustaleniu środków wagi, które minimalizują błąd na wyjściu, można obliczyć za pomocą liniowego rozwiązania pseudoodwrotnego : ${\displaystyle c_{i}}$

${\displaystyle \mathbf {w} =\mathbf {G} ^{+}\mathbf {b} }$,

gdzie wpisy G są wartościami radialnych funkcji bazowych obliczonych w punktach : . ${\displaystyle x_{i}}$${\displaystyle g_{ji}=\rho (||x_{j}-c_{i}||)}$

Istnienie tego liniowego rozwiązania oznacza, że ​​w przeciwieństwie do wielowarstwowych sieci perceptronowych (MLP), sieci RBF mają wyraźny minimalizator (gdy centra są ustalone).

Gradientowy trening z ciężarami liniowymi

Innym możliwym algorytmem uczącym jest zejście gradientowe . W treningu zejścia w gradiencie, ciężary są korygowane w każdym kroku, przesuwając je w kierunku przeciwnym do gradientu funkcji celu (co pozwala na znalezienie minimum funkcji celu),

${\displaystyle \mathbf {w} (t+1)=\mathbf {w} (t)-\nu {\frac {d}{d\mathbf {w} }}H_{t}(\mathbf {w} )}$

gdzie jest „parametrem uczenia się”. ${\displaystyle \nu }$

W przypadku uczenia wag liniowych , algorytm przyjmuje postać ${\displaystyle a_{i}}$

${\displaystyle a_{i}(t+1)=a_{i}(t)+\nu {\big [}y(t)-\varphi {\big (}\mathbf {x} (t),\mathbf {w} {\big )}{\big ]}\rho {\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right\Vert {\big )}}$

w przypadku nieznormalizowanym i

${\displaystyle a_{i}(t+1)=a_{i}(t)+\nu {\big [}y(t)-\varphi {\big (}\mathbf {x} (t),\mathbf {w} {\big )}{\big ]}u{\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right\Vert {\big )}}$

w znormalizowanym przypadku.

W przypadku lokalnych architektur liniowych trening z gradientem to

${\displaystyle e_{ij}(t+1)=e_{ij}(t)+\nu {\big [}y(t)-\varphi {\big (}\mathbf {x} (t),\mathbf {w} {\big )}{\big ]}v_{ij}{\big (}\mathbf {x} (t)-\mathbf {c} _{i}{\big )}}$

Szkolenie operatora projekcji ciężarów liniowych

W przypadku uczenia wag liniowych i , algorytm staje się ${\displaystyle a_{i}}$${\displaystyle e_{ij}}$

${\displaystyle a_{i}(t+1)=a_{i}(t)+\nu {\big [}y(t)-\varphi {\big (}\mathbf {x} (t),\mathbf {w} {\big )}{\big ]}{\frac {\rho {\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right\Vert {\big )}}{\sum _{i=1}^{N}\rho ^{2}{\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right\Vert {\big )}}}}$

w przypadku nieznormalizowanym i

${\displaystyle a_{i}(t+1)=a_{i}(t)+\nu {\big [}y(t)-\varphi {\big (}\mathbf {x} (t),\mathbf {w} {\big )}{\big ]}{\frac {u{\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right\Vert {\big )}}{\sum _{i=1}^{N}u^{2}{\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right\Vert {\big )}}}}$

w znormalizowanym przypadku i

${\displaystyle e_{ij}(t+1)=e_{ij}(t)+\nu {\big [}y(t)-\varphi {\big (}\mathbf {x} (t),\mathbf {w} {\big )}{\big ]}{\frac {v_{ij}{\big (}\mathbf {x} (t)-\mathbf {c} _{i}{\big )}}{\sum _{i=1}^{N}\sum _{j=1}^{n}v_{ij}^{2}{\big (}\mathbf {x} (t)-\mathbf {c} _{i}{\big )}}}}$

w przypadku lokalno-liniowym.

Dla jednej podstawowej funkcji, szkolenie operatora projekcji sprowadza się do metody Newtona .

Rysunek 6: Szeregi czasowe mapy logistycznej. Wielokrotna iteracja mapy logistycznej generuje chaotyczny szereg czasowy. Wartości mieszczą się w zakresie od zera do jednego. Wyświetlanych jest tutaj 100 punktów treningowych użytych do trenowania przykładów w tej sekcji. Wagi c to pierwsze pięć punktów z tego szeregu czasowego.

Przykłady

Mapa logistyczna

Podstawowe własności radialnych funkcji bazowych można zilustrować prostą mapą matematyczną, mapą logistyczną , która odwzorowuje na siebie przedział jednostkowy. Może być używany do generowania wygodnego prototypowego strumienia danych. Mapa logistyczna może być wykorzystana do badania aproksymacji funkcji , przewidywania szeregów czasowych i teorii sterowania . Mapa wywodzi się z dziedziny dynamiki populacji i stała się prototypem chaotycznych szeregów czasowych. Mapę, w całkowicie chaotycznym reżimie, podaje

${\displaystyle x(t+1)\ {\stackrel {\mathrm {def} }{=}}\ f\left[x(t)\right]=4x(t)\left[1-x(t)\right]}$

gdzie t jest indeksem czasu. Wartość x w czasie t+1 jest funkcją paraboliczną x w czasie t. To równanie reprezentuje podstawową geometrię chaotycznego szeregu czasowego generowanego przez mapę logistyczną.

Generowanie szeregów czasowych z tego równania jest problemem postępującym . Poniższe przykłady ilustrują problem odwrotny ; identyfikacja podstawowej dynamiki lub fundamentalnego równania mapy logistycznej z przykładowych szeregów czasowych. Celem jest znalezienie oszacowania

${\displaystyle x(t+1)=f\left[x(t)\right]\approx \varphi (t)=\varphi \left[x(t)\right]}$

dla fa.

Przybliżenie funkcji

Nieznormalizowane promieniowe funkcje bazowe

Architektura jest

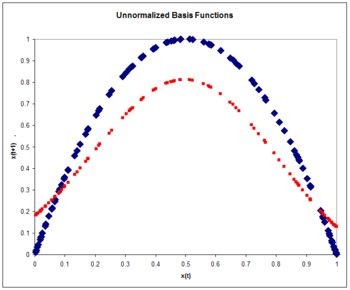
Rysunek 7: Nieznormalizowane funkcje bazowe. Mapa logistyczna (kolor niebieski) i przybliżenie do mapy logistycznej (kolor czerwony) po jednym przejściu przez zbiór uczący.

${\displaystyle \varphi (\mathbf {x} )\ {\stackrel {\mathrm {def} }{=}}\ \sum _{i=1}^{N}a_{i}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}$

gdzie

${\displaystyle \rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}=\exp \left[-\beta _{i}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert ^{2}\right]=\exp \left[-\beta _{i}\left(x(t)-c_{i}\right)^{2}\right]}$.

Ponieważ dane wejściowe są skalarem, a nie wektorem , wymiar wejściowy jest jeden. Wybieramy liczbę funkcji bazowych jako N=5 i wielkość zbioru treningowego na 100 przykładów generowanych przez chaotyczne szeregi czasowe. Za wagę przyjmuje się stałą równą 5. Wagi stanowią pięć przykładów z szeregu czasowego. Wagi są szkolone ze szkoleniem operatora projekcji: ${\displaystyle \beta }$${\displaystyle c_{i}}$${\displaystyle a_{i}}$

${\displaystyle a_{i}(t+1)=a_{i}(t)+\nu {\big [}x(t+1)-\varphi {\big (}\mathbf {x} (t),\mathbf {w} {\big )}{\big ]}{\frac {\rho {\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right\Vert {\big )}}{\sum _{i=1}^{N}\rho ^{2}{\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right\Vert {\big )}}}}$

gdzie współczynnik uczenia się wynosi 0,3. Trening odbywa się przy jednym przejściu przez 100 punktów treningowych. Błąd RMS wynosi 0,15. ${\displaystyle \nu }$

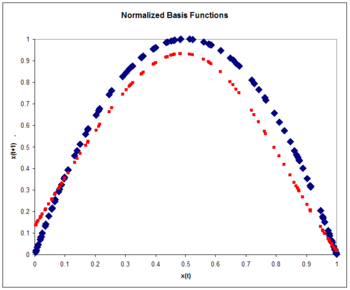
Rysunek 8: Znormalizowane funkcje bazowe. Mapa logistyczna (kolor niebieski) i przybliżenie do mapy logistycznej (kolor czerwony) po jednym przejściu przez zbiór uczący. Zwróć uwagę na poprawę w stosunku do przypadku nieznormalizowanego.

Znormalizowane promieniowe funkcje bazowe

Znormalizowana architektura RBF to

${\displaystyle \varphi (\mathbf {x} )\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\sum _{i=1}^{N}a_{i}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}{\sum _{i=1}^{N}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}}=\sum _{i=1}^{N}a_{i}u{\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}$

gdzie

${\displaystyle u{\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}{\sum _{i=1}^{N}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}}}$.

Jeszcze raz:

${\displaystyle \rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}=\exp \left[-\beta \left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert ^{2}\right]=\exp \left[-\beta \left(x(t)-c_{i}\right)^{2}\right]}$.

Ponownie wybieramy liczbę funkcji bazowych na pięć i wielkość zbioru treningowego na 100 przykładów wygenerowanych przez chaotyczne szeregi czasowe. Za wagę przyjmuje się stałą równą 6. Wagi stanowią pięć przykładów z szeregu czasowego. Ciężary są szkolone ze szkoleniem operatora projekcji: ${\displaystyle \beta }$${\displaystyle c_{i}}$${\displaystyle a_{i}}$

${\displaystyle a_{i}(t+1)=a_{i}(t)+\nu {\big [}x(t+1)-\varphi {\big (}\mathbf {x} (t),\mathbf {w} {\big )}{\big ]}{\frac {u{\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right\Vert {\big )}}{\sum _{i=1}^{N}u^{2}{\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right\Vert {\big )}}}}$

gdzie współczynnik uczenia się ponownie przyjmuje się za 0,3. Trening odbywa się przy jednym przejściu przez 100 punktów treningowych. Błąd RMS na zestawie testowym 100 egzemplarzy wynosi 0,084, mniejszy niż nieznormalizowanych błędu. Normalizacja zapewnia poprawę dokładności. Zazwyczaj dokładność ze znormalizowanymi funkcjami bazowymi wzrasta jeszcze bardziej w porównaniu z funkcjami nieznormalizowanymi wraz ze wzrostem wymiaru wejściowego. ${\displaystyle \nu }$

Rysunek 9: Znormalizowane funkcje bazowe. Mapa logistyczna (kolor niebieski) i aproksymacja mapy logistycznej (kolor czerwony) w funkcji czasu. Zauważ, że przybliżenie jest dobre tylko dla kilku kroków czasowych. Jest to ogólna charakterystyka chaotycznych szeregów czasowych.

Przewidywanie szeregów czasowych

Po oszacowaniu podstawowej geometrii szeregu czasowego, jak w poprzednich przykładach, prognozę dla szeregu czasowego można wykonać za pomocą iteracji:

${\displaystyle \varphi (0)=x(1)}$

${\displaystyle {x}(t)\approx \varphi (t-1)}$

${\displaystyle {x}(t+1)\approx \varphi (t)=\varphi [\varphi (t-1)]}$.

Na rysunku przedstawiono porównanie rzeczywistych i szacowanych szeregów czasowych. Szacowane szeregi czasowe rozpoczynają się w czasie zero z dokładną wiedzą o x(0). Następnie wykorzystuje oszacowanie dynamiki do aktualizacji oszacowania szeregu czasowego dla kilku przedziałów czasowych.

Pamiętaj, że oszacowanie jest dokładne tylko dla kilku kroków czasowych. Jest to ogólna charakterystyka chaotycznych szeregów czasowych. Jest to właściwość wrażliwej zależności od warunków początkowych wspólnych dla chaotycznych szeregów czasowych. Mały początkowy błąd jest z czasem wzmacniany. Miarą rozbieżności szeregów czasowych o niemal identycznych warunkach początkowych jest wykładnik Lapunowa .

Kontrola chaotycznych szeregów czasowych

Rysunek 10: Kontrola mapy logistycznej. System może ewoluować naturalnie w 49 krokach czasowych. W momencie 50 sterowanie jest włączone. Żądana trajektoria dla szeregu czasowego jest czerwona. Kontrolowany system uczy się podstawowej dynamiki i kieruje szeregi czasowe do pożądanego wyniku. Architektura jest taka sama, jak w przykładzie przewidywania szeregów czasowych.

Zakładamy, że wyjściem mapy logistycznej można manipulować za pomocą parametru kontrolnego takiego, że ${\displaystyle c[x(t),t]}$

${\displaystyle {x}_{}^{}(t+1)=4x(t)[1-x(t)]+c[x(t),t]}$.

Celem jest taki dobór parametru kontrolnego, aby doprowadzić szereg czasowy do pożądanej wartości wyjściowej . Można to zrobić, jeśli wybierzemy parametr kontrolny, który ma być ${\displaystyle d(t)}$

${\displaystyle c_{}^{}[x(t),t]\ {\stackrel {\mathrm {def} }{=}}\ -\varphi [x(t)]+d(t+1)}$

gdzie

${\displaystyle y[x(t)]\approx f[x(t)]=x(t+1)-c[x(t),t]}$

jest przybliżeniem do podstawowej naturalnej dynamiki systemu.

Algorytm uczenia jest podany przez

${\displaystyle a_{i}(t+1)=a_{i}(t)+\nu \varepsilon {\frac {u{\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right\Vert {\big )}}{\sum _{i=1}^{N}u^{2}{\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right\Vert {\big )}}}}$

gdzie

${\displaystyle \varepsilon \ {\stackrel {\mathrm {def} }{=}}\ f[x(t)]-\varphi [x(t)]=x(t+1)-c[x(t),t]-\varphi [x(t)]=x(t+1)-d(t+1)}$.

Zobacz też

• Jądro promieniowej funkcji bazowej
• nauka oparta na instancjach
• Adaptacyjna tablica in situ
• Analityka predykcyjna
• Teoria chaosu
• Hierarchiczny RBF
• Kontroler artykulacji modelu móżdżku
• Błyskawicznie wytrenowane sieci neuronowe

Bibliografia

Dalsza lektura

• J. Moody i CJ Darken, „Szybkie uczenie się w sieciach lokalnie dostrojonych jednostek przetwarzania”, Neural Computation, 1, 281-294 (1989). Zobacz także Radialne sieci funkcyjne według Moody i Darken
• T. Poggio i F. Girosi, „ Sieci dla aproksymacji i uczenia się ”, Proc. IEEE 78(9), 1484-1487 (1990).
• Roger D. Jones , YC Lee, CW Barnes, GW Flake, K. Lee, PS Lewis i S. Qian, ? Aproksymacja funkcji i przewidywanie szeregów czasowych za pomocą sieci neuronowych ,? Proceedings of the International Joint Conference on Neural Networks, 17–21 czerwca, s. I-649 (1990).
• Martina D. Buhmanna (2003). Radialne funkcje bazowe: teoria i implementacje . Uniwersytet Cambridge. Numer ISBN 0-521-63338-9.
• Yee, Paul V. i Haykin, Simon (2001). Uregulowane sieci funkcji radialnych: teoria i zastosowania . Johna Wileya. Numer ISBN 0-471-35349-3.
• John R. Davies, Stephen V. Coggeshall, Roger D. Jones i Daniel Schutzer, „Inteligentne systemy bezpieczeństwa”, w: Freedman, Roy S., Flein, Robert A. i Lederman, Jess, Editors (1995). Sztuczna inteligencja na rynkach kapitałowych . Chicago: Irwin. Numer ISBN 1-55738-811-3.CS1 maint: multiple names: authors list (link)
• Szymona Haykina (1999). Sieci neuronowe: kompleksowa podstawa (2nd ed.). Upper Saddle River, NJ: Prentice Hall. Numer ISBN 0-13-908385-5.
• S. Chen, CFN Cowan i PM Grant, „ Algorytm uczenia ortogonalnego najmniejszych kwadratów dla sieci z funkcją podstawy promieniowej ”, IEEE Transactions on Neural Networks, tom 2, nr 2 (marzec) 1991.