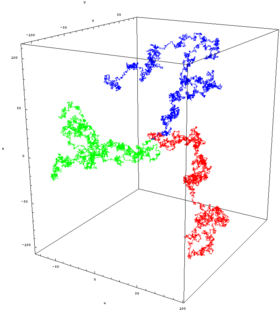
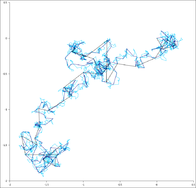
Losowy spacer - Random walk

Część serii o statystykach
Teoria prawdopodobieństwa
Prawdopodobieństwo Aksjomaty Determinizm System Indeterminizm Losowość
Przestrzeń prawdopodobieństwa Przestrzeń próbna Wydarzenie Zbiorowo wyczerpujące wydarzenia Wydarzenie podstawowe Wzajemna wyłączność Wynik Singel Eksperyment Proces Bernoulliego Rozkład prawdopodobieństwa Dystrybucja Bernoulliego Rozkład dwumianowy Normalna dystrybucja Miara prawdopodobieństwa Zmienna losowa Proces Bernoulliego Ciągły lub dyskretny Wartość oczekiwana Łańcuch Markowa Zaobserwowana wartość Losowy spacer Proces stochastyczny
Wydarzenie uzupełniające Wspólne prawdopodobieństwo krańcowe prawdopodobieństwo Warunkowe prawdopodobieństwo
Niezależność Warunkowa niezależność Prawo całkowitego prawdopodobieństwa Prawo wielkich liczb Twierdzenie Bayesa Nierówność Boole'a
Schemat Venna Schemat drzewa
v T mi

Pięć ośmiostopniowych losowych spacerów od centralnego punktu. Niektóre ścieżki wydają się krótsze niż osiem kroków, gdzie trasa podwoiła się. ( wersja animowana )

W matematyce , o błądzenia losowego jest matematyczny obiekt , znany jako stochastyczny lub procesu losowego , który opisuje ścieżkę, która składa się z kolejnych przypadkowych kroków na jakiejś matematycznej przestrzeni , takich jak liczby całkowite .

Podstawowym przykładem błądzenia losowego jest błądzenie losowe na osi liczb całkowitych , które zaczyna się od 0 i na każdym kroku przesuwa się o +1 lub -1 z równym prawdopodobieństwem . Inne przykłady obejmują ścieżkę śledzoną przez molekułę, gdy porusza się ona w cieczy lub gazie (patrz ruchy Browna ), ścieżkę poszukiwań żerujących zwierząt, cenę wahających się akcji i status finansowy hazardzisty : wszystko można przybliżyć przez modele błądzenia losowego, nawet jeśli w rzeczywistości mogą nie być losowe. ${\ Displaystyle \ mathbb {Z}}$

Jak pokazują te przykłady, przypadkowe spacery mają zastosowanie w inżynierii i wielu dziedzinach nauki, w tym ekologii , psychologii , informatyce , fizyce , chemii , biologii , ekonomii i socjologii . Spacery losowe wyjaśniają obserwowane zachowania wielu procesów w tych dziedzinach, a tym samym służą jako podstawowy model rejestrowanej aktywności stochastycznej. Jako bardziej matematyczne zastosowanie, wartość π można aproksymować za pomocą błądzenia losowego w środowisku modelowania agentowego . Termin błądzenie losowe został po raz pierwszy wprowadzony przez Karla Pearsona w 1905 roku.

Interesujące są różne rodzaje spacerów losowych, które mogą różnić się na kilka sposobów. Sam termin najczęściej odnosi się do specjalnej kategorii łańcuchów Markowa , ale wiele procesów zależnych od czasu określa się mianem spacerów losowych, z modyfikatorem wskazującym na ich specyficzne właściwości. Spacery losowe (Markov lub nie) mogą również odbywać się w różnych przestrzeniach: powszechnie badane obejmują wykresy , inne na liczbach całkowitych lub na prostej, w płaszczyźnie lub w wyższych przestrzeniach wektorowych, na zakrzywionych powierzchniach lub w wyższych wymiarach riemannowskich rozmaitości , a także na grupach skończonych, skończenie generowanych lub Lie . Można również manipulować parametrem czasu. W najprostszym kontekście spacer jest w czasie dyskretnym, czyli ciągu zmiennych losowych ( X
_T) = ( X
₁, X
₂, ...) indeksowane liczbami naturalnymi. Możliwe jest jednak również zdefiniowanie losowych spacerów, które wykonują swoje kroki w losowych momentach, a w tym przypadku pozycja X
_Tmusi być zdefiniowany dla wszystkich czasów t ∈ [0,+∞) . Konkretne przypadki lub granice błądzeń losowych obejmują modele lotu Lévy'ego i modele dyfuzji , takie jak ruchy Browna .

Spacery losowe są podstawowym tematem dyskusji o procesach Markowa. Ich badania matematyczne były rozległe. W celu ilościowego określenia ich zachowania wprowadzono kilka właściwości, w tym rozkłady rozproszenia, czasy pierwszego przejścia lub trafienia, współczynniki napotkania, powtarzalność lub przemijanie.

Kratowy losowy spacer

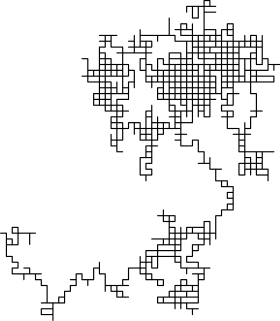
Popularnym modelem błądzenia losowego jest błąd błądzenia losowego po regularnej sieci, w którym na każdym kroku lokalizacja przeskakuje do innego miejsca zgodnie z pewnym rozkładem prawdopodobieństwa. W prostym spacerze losowym lokalizacja może przeskoczyć tylko do sąsiednich miejsc sieci, tworząc ścieżkę sieciową . W prostym symetrycznym błądzeniu losowym po lokalnie skończonej sieci prawdopodobieństwa przeskoku lokalizacji do każdego z jej bezpośrednich sąsiadów są takie same. Najlepiej zbadanym przykładem jest błądzenie losowe po d- wymiarowej sieci liczb całkowitych (nazywanej czasami siecią hipersześcienną) . ${\ Displaystyle \ mathbb {Z} ^ {d}}$

Jeśli przestrzeń stanów jest ograniczona do wymiarów skończonych, model błądzenia losowego nazywamy prostym obramowanym symetrycznym błądzeniem losowym, a prawdopodobieństwa przejścia zależą od położenia stanu, ponieważ w stanach brzegowych i narożnych ruch jest ograniczony.

Jednowymiarowy losowy spacer

Elementarna przykład losowej odległości jest losowo chodzić na całkowitą osi liczbowej, zaczynający się od 0 i każdy porusza się w kroku +1 lub -1 równego prawdopodobieństwa. ${\ Displaystyle \ mathbb {Z}}$

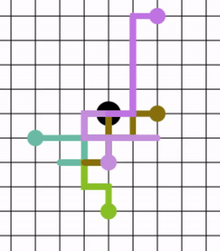
Ten spacer można zilustrować w następujący sposób. Znacznik umieszcza się na zero na osi liczbowej i rzuca uczciwą monetą. Jeśli wyląduje na głowach, znacznik przesuwa się o jedną jednostkę w prawo. Jeśli wyląduje na ogonie, znacznik przesuwa się o jedną jednostkę w lewo. Po pięciu rzutach znacznik może teraz znajdować się na -5, -3, -1, 1, 3, 5. Z pięcioma rzutami, trzema orłami i dwoma resztkami, w dowolnej kolejności, wyląduje na 1. Jest 10 sposobów lądowanie na 1 (przez odwrócenie trzech orłów i dwóch reszek), 10 sposobów lądowania na −1 (przez odwrócenie trzech ogonów i dwóch orłów), 5 sposobów lądowania na 3 (przez odwrócenie czterech orłów i jednego ogona), 5 sposobów lądowania na -3 (przez odwrócenie czterech ogonów i jedną głowę), 1 sposób lądowania na 5 (przez odwrócenie pięciu orłów) i 1 sposób lądowania na -5 (przez odwrócenie pięciu ogonów). Poniższy rysunek przedstawia ilustrację możliwych wyników 5 przewrotów.

Wszystkie możliwe wyniki błądzenia losowego po 5 rzutach uczciwą monetą

Losowy spacer w dwóch wymiarach ( wersja animowana )

Losowy spacer w dwóch wymiarach z 25 tysiącami kroków ( wersja animowana )

Losowy spacer w dwóch wymiarach z dwoma milionami jeszcze mniejszych kroków. Ten obraz został wygenerowany w taki sposób, że punkty, przez które częściej się przemierzają, są ciemniejsze. W granicy, dla bardzo małych kroków, uzyskuje się ruch Browna .

Aby określić ten spacer formalnie podjąć niezależnych zmiennych losowych , gdzie każda zmienna jest albo 1 albo -1, z prawdopodobieństwem 50% dla każdej wartości i ustaw i seria nazywa się prosty losowy spacer . Ta seria (suma ciągu -1s i 1s) daje przebytą odległość netto, jeśli każda część spaceru ma długość jeden. Oczekiwanie na zero. Oznacza to, że wraz ze wzrostem liczby rzutów średnia wszystkich rzutów monetą zbliża się do zera. Wynika to ze skończonej addytywności oczekiwania: ${\displaystyle Z_{1},Z_{2},\kropki}$${\displaystyle S_{0}=0\\!}$${\ Displaystyle S_ {n} = \ suma _ {j = 1} ^ {n} Z_ {j}.}$ ${\ Displaystyle \ {S_ {n} \} \, \!}$${\ Displaystyle \ mathbb {Z}}$ ${\ Displaystyle E (S_ {n}) \, \!}$${\displaystyle S_{n}\\!}$

${\ Displaystyle E (S_ {n}) = \ suma _ {j = 1} ^ {n} E (Z_ {j}) = 0.}$

Podobne obliczenie, wykorzystujące niezależność zmiennych losowych oraz fakt, że , pokazuje, że: ${\ Displaystyle E (Z_ {n} ^ {2}) = 1}$

${\ Displaystyle E (S_ {n} ^ {2}) = \ suma _ {i = 1} ^ {n} E (Z_ {i} ^ {2}) + 2 \ suma _ {1 \ równoważnik i <j \leq n}E(Z_{i}Z_{j})=n.}$

Wskazuje to , że oczekiwana odległość translacji po n krokach powinna być rzędu . W rzeczywistości, ${\ Displaystyle E (| S_ {n} |) \ \!}$ ${\displaystyle {\sqrt {n}}}$

${\ Displaystyle \ lim _ {n \ do \ infty} {\ Frac {E (| S_ {n} |)} {\ sqrt {n}}} = {\ sqrt {\ Frac {2} {\ pi}} }.}$

Wynik ten pokazuje, że dyfuzja jest nieefektywna w przypadku mieszania ze względu na sposób, w jaki pierwiastek kwadratowy zachowuje się dla dużych . ${\ Displaystyle N}$

Ile razy losowy spacer przekroczy linię graniczną, jeśli pozwoli się na kontynuowanie marszu w nieskończoność? Proste błądzenie losowe przetnie każdy punkt nieskończoną liczbę razy. Wynik ten ma wiele nazw: zjawisko przechodzenia przez poziomy , nawrót lub ruina hazardzisty . Powód nazwiska jest następujący: hazardzista ze skończoną ilością pieniędzy w końcu przegra, grając uczciwą grę z bankiem z nieskończoną ilością pieniędzy. Pieniądze gracza wykonają losowy spacer i w pewnym momencie osiągną zero, a gra się skończy. ${\ Displaystyle \ mathbb {Z}}$

Jeśli i b są liczbami całkowitymi dodatnimi, to oczekiwana liczba czynności, aż jednowymiarowej prosty błądzenia losowego począwszy od pierwszych trafień 0 b lub - jest ab . Prawdopodobieństwo, że to błądzenie trafi b przed − a wynosi , co można wyprowadzić z faktu, że prosty błądzenie losowe jest martyngałem . ${\displaystyle a/(a+b)}$

Niektóre z powyższych wyników można wyprowadzić z własności trójkąta Pascala . Liczba różnych spacerów n kroków, gdzie każdy krok to +1 lub -1 to 2 ⁿ . W przypadku prostego błądzenia losowego każdy z tych spacerów jest jednakowo prawdopodobny. Aby S _n było równe liczbie k , konieczne i wystarczające jest, aby liczba +1 w spacerze przekraczała liczbę -1 o k . Wynika z tego, że +1 musi występować ( n  +  k )/2 razy wśród n kroków spaceru, stąd liczba spacerów spełniających jest równa liczbie sposobów wyboru ( n  +  k )/2 elementów ze zbioru n elementów, oznaczonych . Aby to miało znaczenie, konieczne jest, aby n  +  k było liczbą parzystą, co oznacza, że n i k są albo parzyste, albo nieparzyste. Dlatego prawdopodobieństwo równe . Reprezentując wpisy trójkąta Pascala w postaci silni i stosując wzór Stirlinga , można uzyskać dobre oszacowanie tych prawdopodobieństw dla dużych wartości . ${\ Displaystyle S_ {n} = k}$${\ Displaystyle n \ wybierz (n + k)/2}$${\ Displaystyle S_ {n} = k}$${\ Displaystyle 2 ^ {-n} {n \ wybierz (n + k)/2}}$${\ Displaystyle n}$

Jeśli przestrzeń jest ograniczona do + dla zwięzłości, liczba sposobów, w jakie błądzenie losowe wyląduje na dowolnej liczbie z pięcioma rzutami, może być pokazana jako {0,5,0,4,0,1}. ${\ Displaystyle \ mathbb {Z}}$

Ta zależność z trójkątem Pascala jest pokazana dla małych wartości n . Na zerowych zakrętach jedyną możliwością będzie pozostanie na zero. Jednak w jednej turze jest jedna szansa na wylądowanie na -1 lub jedna szansa na wylądowanie na 1. W dwóch turach znacznik na 1 może przesunąć się na 2 lub z powrotem do zera. Znacznik na -1 może przesunąć się do -2 lub z powrotem do zera. Dlatego istnieje jedna szansa na lądowanie na -2, dwie szanse na lądowanie na zero i jedna szansa na lądowanie na 2.

k	-5	-4	-3	-2	-1	0	1	2	3	4	5
${\displaystyle P[S_{0}=k]}$						1
${\displaystyle 2P[S_{1}=k]}$					1		1
${\ Displaystyle 2 ^ {2} P [S_ {2} = k]}$				1		2		1
${\ Displaystyle 2 ^ {3}P[S_{3}=k]}$			1		3		3		1
${\ Displaystyle 2 ^ {4} P [S_ {4} = k]}$		1		4		6		4		1
${\ Displaystyle 2 ^ {5} P [S_ {5} = k]}$	1		5		10		10		5		1

Centralne twierdzenie graniczne i Prawo iterowanego logarytmu opisać ważne aspekty zachowań prostych losowych spacerów . W szczególności to pierwsze pociąga za sobą, że wraz ze wzrostem n prawdopodobieństwa (proporcjonalne do liczb w każdym wierszu) zbliżają się do rozkładu normalnego . ${\ Displaystyle \ mathbb {Z}}$

Jako bezpośrednie uogólnienie można rozważyć błądzenie losowe po sieciach krystalicznych (nieskończenie krotnie abelowe obejmujące grafy nad grafami skończonymi). W rzeczywistości możliwe jest ustalenie centralnego twierdzenia granicznego i twierdzenia o dużym odchyleniu w tym ustawieniu.

Jako łańcuch Markowa

Jednowymiarowe błądzenie losowe można również traktować jako łańcuch Markowa, którego przestrzeń stanów jest dana przez liczby całkowite. Dla pewnej liczby p spełniającej , podane są prawdopodobieństwa przejścia (prawdopodobieństwo Pi _,j przejścia ze stanu i do stanu j ) za pomocą ${\ Displaystyle i = 0, \ pm 1, \ pm 2, \ kropki.}$${\displaystyle \,0<p<1}$

${\ Displaystyle \, P_ {i, i + 1} = p = 1-P_ {i, i-1}.}$

Uogólnienie heterogeniczne

Wyższe wymiary

Trzy przypadkowe spacery w trzech wymiarach

W wyższych wymiarach zbiór losowo chodzących punktów ma ciekawe właściwości geometryczne. W rzeczywistości otrzymujemy fraktal dyskretny , czyli zbiór, który wykazuje stochastyczne samopodobieństwo w dużych skalach. W małych skalach można zaobserwować „postrzępioność” wynikającą z siatki, po której wykonywany jest spacer. Dwie książki Lawlera, o których mowa poniżej, są dobrym źródłem na ten temat. Trajektoria spaceru losowego to zbiór odwiedzonych punktów, traktowany jako zbiór bez względu na to, kiedy spacer dotarł do punktu. W jednym wymiarze trajektoria to po prostu wszystkie punkty pomiędzy minimalną wysokością a maksymalną wysokością, jaką osiągnął spacer (oba są średnio rzędu ). ${\displaystyle {\sqrt {n}}}$

Aby zobrazować dwuwymiarowy przypadek, można wyobrazić sobie osobę chodzącą losowo po mieście. Miasto jest praktycznie nieskończone i ułożone w kwadratową siatkę chodników. Na każdym skrzyżowaniu osoba losowo wybiera jedną z czterech możliwych tras (w tym tę, z której pierwotnie podróżowała). Formalnie jest to błądzenie losowe po zbiorze wszystkich punktów na płaszczyźnie o współrzędnych całkowitych .

Czy dana osoba kiedykolwiek wróci do początkowego punktu wyjścia? Jest to dwuwymiarowy odpowiednik omówionego powyżej problemu przejazdów kolejowych. W 1921 George Pólya udowodnił, że osoba prawie na pewno będzie w dwuwymiarowym błądzeniu losowym, ale dla 3 wymiarów lub wyższych prawdopodobieństwo powrotu do miejsca pochodzenia maleje wraz ze wzrostem liczby wymiarów. W 3 wymiarach prawdopodobieństwo spada do około 34%. Wiadomo, że matematyk Shizuo Kakutani odniósł się do tego wyniku następującym cytatem: „Pijany człowiek odnajdzie drogę do domu, ale pijany ptak może zgubić się na zawsze”.

Inną odmianą tego pytania, które również zadała Pólya, jest: jeśli dwie osoby opuszczą ten sam punkt wyjścia, to czy kiedykolwiek się spotkają? Można wykazać, że różnica między ich lokalizacjami (dwa niezależne losowe spacery) jest również prostym błądzeniem losowym, więc prawie na pewno spotkają się ponownie w spacerze dwuwymiarowym, ale dla 3 wymiarów i wyższych prawdopodobieństwo maleje wraz z liczbą wymiary. Paul Erdős i Samuel James Taylor pokazali również w 1960 roku, że dla wymiarów mniejszych lub równych 4 dwa niezależne spacery losowe zaczynające się od dowolnych dwóch punktów mają nieskończenie wiele przecięć prawie na pewno, ale dla wymiarów większych niż 5 prawie na pewno przecinają się tylko skończenie często .

Asymptotyczna funkcja dwuwymiarowego błądzenia losowego wraz ze wzrostem liczby kroków jest określona przez rozkład Rayleigha . Rozkład prawdopodobieństwa jest funkcją promienia od początku, a długość kroku jest stała dla każdego kroku.

${\ Displaystyle P (r) = {\ Frac {2r} {N}} e ^ {-r ^ {2} / N}}$

Związek z procesem Wienera

Symulowane kroki przybliżające proces Wienera w dwóch wymiarach

Procesu Wienera jest procesem stochastycznym z podobnym postępowaniu z ruchami Browna , zjawisko fizyczne minutę cząstek rozpraszającego się w złożu fluidalnym. (Czasami proces Wienera nazywany jest „ruchem Browna”, chociaż ściśle mówiąc jest to pomylenie modelu z modelowanym zjawiskiem.)

Proces Wienera jest limitem skalowania błądzenia losowego w wymiarze 1. Oznacza to, że jeśli wykonasz błądzenie losowe z bardzo małymi krokami, uzyskasz przybliżenie do procesu Wienera (i mniej dokładnie do ruchu Browna). Aby być bardziej precyzyjnym, jeśli rozmiar kroku wynosi ε, należy wykonać spacer o długości L /ε ^{2 ,} aby przybliżyć długość Wienera L . Ponieważ rozmiar kroku dąży do 0 (a liczba kroków rośnie proporcjonalnie), błądzenie losowe zbiega się w odpowiednim sensie do procesu Wienera. Formalnie, jeśli B jest przestrzenią wszystkich ścieżek o długości L z topologią maksymalną, a M jest przestrzenią miary nad B z topologią normy, to zbieżność zachodzi w przestrzeni M . Podobnie proces Wienera w kilku wymiarach jest limitem skalowania błądzenia losowego w tej samej liczbie wymiarów.

Błądzenie losowe to dyskretny fraktal (funkcja o wymiarach całkowitych; 1, 2, ...), ale trajektoria procesu Wienera jest prawdziwym fraktalem i istnieje związek między nimi. Na przykład, wybierz błądzenie losowe, aż trafi na okrąg o promieniu r razy długość kroku. Średnia liczba kroków, które wykonuje to r ² . Ten fakt jest dyskretną wersją faktu, że spacer po procesie Wienera jest fraktalem drugiego wymiaru Hausdorffa  .

W dwóch wymiarach średnia liczba punktów, jakie to samo błądzenie losowe ma na granicy swojej trajektorii wynosi r ^4/3 . Odpowiada to faktowi, że granica trajektorii procesu Wienera jest fraktalem o wymiarze 4/3, fakt przewidziany przez Mandelbrota za pomocą symulacji, ale udowodniony dopiero w 2000 roku przez Lawlera , Schramma i Wernera .

Proces Wienera cieszy się wieloma symetriami błądzenie losowe nie. Na przykład błądzenie procesu Wienera jest niezmiennicze w stosunku do obrotów, ale błądzenie losowe nie, ponieważ podstawowa siatka nie jest (spacer losowy jest niezmienny w stosunku do obrotów o 90 stopni, ale procesy Wienera są niezmiennicze w stosunku do obrotów o np. 17 stopni także). Oznacza to, że w wielu przypadkach problemy z błądzenia losowego są łatwiejsze do rozwiązania, przekładając je na proces Wienera, rozwiązując problem w tym miejscu, a następnie tłumacząc z powrotem. Z drugiej strony niektóre problemy są łatwiejsze do rozwiązania za pomocą spacerów losowych ze względu na ich dyskretny charakter.

Spacer losowy i proces Wienera mogą być sprzężone , czyli manifestowane na tej samej przestrzeni prawdopodobieństwa w sposób zależny, który wymusza na nich bycie dość blisko siebie. Najprostszym takim sprzężeniem jest osadzanie Skorokhod, ale istnieją bardziej precyzyjne sprzężenia, takie jak twierdzenie o aproksymacji Komlósa–Majora–Tusnády’ego .

Zbieżność błądzenia losowego w kierunku procesu Wienera jest kontrolowana przez centralne twierdzenie graniczne , oraz twierdzenie Donskera . Dla cząstki w znanej pozycji ustalonej w t  = 0, centralne twierdzenie graniczne mówi nam, że po dużej liczbie niezależnych kroków w błądzeniu losowym pozycja chodzika rozkłada się zgodnie z normalnym rozkładem całkowitej wariancji :

${\ Displaystyle \ sigma ^ {2} = {\ Frac {t} {\ delta t}} \ \ varepsilon ^ {2}}$

gdzie t jest czasem, jaki upłynął od rozpoczęcia błądzenia losowego, jest rozmiarem kroku błądzenia losowego i jest czasem, jaki upłynął między dwoma kolejnymi krokami. ${\displaystyle \varepsilon}$${\ Displaystyle \ delta t}$

Odpowiada to Funkcja Greena z równania dyfuzji , że kontrole procesu Wienera, który sugeruje, że po wielu kroków, błądzenia losowego zbieżna w kierunku procesu Wienera.

W 3D wariancja odpowiadająca funkcji Greena równania dyfuzji wynosi:

${\ Displaystyle \ sigma ^ {2} = 6 \ D \ t.}$

Wyrównując tę ​​wielkość z wariancją związaną z pozycją błądzącego losowego, otrzymuje się równoważny współczynnik dyfuzji, który należy wziąć pod uwagę dla asymptotycznego procesu Wienera, do którego błądzenie losowe zbiega się po dużej liczbie kroków:

${\ Displaystyle D = {\ Frac {\ varepsilon ^ {2}} {6 \ delta t}}}$ (ważne tylko w 3D).

Uwaga: dwa wyrażenia powyższej wariancji odpowiadają rozkładowi powiązanemu z wektorem łączącym dwa końce błądzenia losowego w 3D. Wariancja wiąże się do każdego składnika , lub tylko jedną trzecią tej wartości (jeszcze 3D). ${\displaystyle {\vec {R}}}$${\ Displaystyle R_ {x}}$${\displaystyle R_{y}}$${\ Displaystyle R_ {z}}$

Dla 2D:

${\ Displaystyle D = {\ Frac {\ varepsilon ^ {2}} {4 \ delta t}}.}$

Dla 1D:

${\ Displaystyle D = {\ Frac {\ varepsilon ^ {2}} {2 \ delta t}}.}$

Gaussowski losowy spacer

Błądzenie losowe o rozmiarze kroku, który zmienia się zgodnie z rozkładem normalnym, jest używany jako model dla danych szeregów czasowych w świecie rzeczywistym, takich jak rynki finansowe. Na przykład wzór Blacka-Scholesa do modelowania cen opcji wykorzystuje błądzenie losowe Gaussa jako podstawowe założenie.

Tutaj rozmiar kroku jest odwrotnym skumulowanym rozkładem normalnym, gdzie 0 ≤  z  ≤ 1 jest liczbą losową o rozkładzie jednostajnym, a μ i σ są odpowiednio średnią i odchyleniem standardowym rozkładu normalnego. ${\ Displaystyle \ Phi ^ {-1} (z \ mu \ sigma)}$

Jeśli μ jest niezerowe, błądzenie losowe będzie się różnić w zależności od trendu liniowego. Jeśli v _s jest wartością początkową błądzenia losowego, oczekiwana wartość po n krokach wyniesie v _s + n μ.

W szczególnym przypadku, gdy μ jest równe zero, po n krokach rozkład prawdopodobieństwa odległości translacji jest określony przez N (0, n σ ² ), gdzie N () jest zapisem rozkładu normalnego, n jest liczbą kroków , a σ pochodzi z odwrotnego skumulowanego rozkładu normalnego podanego powyżej.

Dowód: błądzenie losowe Gaussa można traktować jako sumę ciągu niezależnych i identycznie rozłożonych zmiennych losowych, X _i z odwrotnego skumulowanego rozkładu normalnego ze średnią równą zero i σ pierwotnego odwrotnego skumulowanego rozkładu normalnego:

Z = ,${\ Displaystyle \ suma _ {i = 0} ^ {n} {X_ {i}}}$

ale mamy rozkład dla sumy dwóch niezależnych zmiennych losowych o rozkładzie normalnym, Z = X + Y, jest określony wzorem

${\displaystyle {\mathcal {N}}}$(μ _X + μ _Y , σ ² _X + σ ² _Y ) (patrz tutaj) .

W naszym przypadku μ _X = μ _Y = 0 i σ ² _X = σ ² _Y = σ ² wydajność

${\displaystyle {\mathcal {N}}}$(0, 2σ ² )

Przez indukcję, dla n kroków mamy

Z ~ (0, n σ ² ).${\displaystyle {\mathcal {N}}}$

Dla kroków rozłożonych zgodnie z dowolnym rozkładem ze średnią zerową i skończoną wariancją (niekoniecznie tylko rozkładem normalnym), średnia kwadratowa odległość translacji po n krokach wynosi

${\ Displaystyle {\ sqrt {E | S_ {n} ^ {2} |}} = \ sigma {\ sqrt {n}}.}$

Ale w przypadku błądzenia losowego Gaussa jest to po prostu odchylenie standardowe rozkładu odległości translacji po n krokach. Stąd, jeśli μ jest równe zeru, a odległość translacji średniej kwadratowej (RMS) jest jednym odchyleniem standardowym, istnieje 68,27% prawdopodobieństwa, że ​​odległość translacji RMS po n krokach spadnie między ± σ . Podobnie istnieje 50% prawdopodobieństwa, że ​​odległość translacji po n krokach spadnie między ± 0.6745σ . ${\displaystyle {\sqrt {n}}}$${\displaystyle {\sqrt {n}}}$

Anomalna dyfuzja

W nieuporządkowanych systemach, takich jak media porowate i fraktale, może nie być proporcjonalna, ale do . Wykładnik ten nazywany jest wykładnikiem anomalnej dyfuzji i może być większy lub mniejszy niż 2. Dyfuzja anomalna może być również wyrażona jako σ _r ² ~ Dt ^α, gdzie α jest parametrem anomalii. Niektóre dyfuzje w losowym środowisku są nawet proporcjonalne do potęgi logarytmu czasu, patrz na przykład chód Synaju lub dyfuzja Broxa. ${\ Displaystyle \ sigma ^ {2}}$${\displaystyle t}$${\ Displaystyle t ^ {2}/d_ {w}}}$${\displaystyle d_{w}}$

Liczba odrębnych witryn

Liczba odrębnych miejsc odwiedzanych przez pojedynczego przypadkowego wędrowca została dokładnie zbadana pod kątem krat kwadratowych i sześciennych oraz fraktali. Wielkość ta jest przydatna do analizy problemów wychwytywania i reakcji kinetycznych. Wiąże się to również z gęstością wibracyjną stanów, procesami reakcji dyfuzyjnych i rozprzestrzenieniem się populacji w ekologii. Uogólnienie tego problemu na liczbę odrębnych miejsc odwiedzanych przez przypadkowych spacerowiczów , zostało ostatnio zbadane dla d-wymiarowych sieci euklidesowych. Liczba odrębnych witryn odwiedzanych przez N spacerowiczów nie jest po prostu związana z liczbą odrębnych witryn odwiedzanych przez każdego spacerowicza. ${\ Displaystyle S (t)}$${\ Displaystyle N}$${\ Displaystyle S_ {N} (t)}$

Wskaźnik informacji

Szybkość informacji o losowym błądzeniu Gaussa w odniesieniu do kwadratu odległości błędu, tj. jego funkcji zniekształcenia kwadratowego , jest dana parametrycznie przez

${\ Displaystyle R (D_ {\ theta}) = {\ Frac {1} {2}} \ int _ {0} ^ {1} \ max \ {0, \ log _ {2} \ lewo (S (\ varphi )/\theta \prawo)\}\,d\varphi ,}$

${\displaystyle D_{\theta}=\int _{0}^{1}\min\{S(\varphi),\theta\}\d\varphi,}$

gdzie . Dlatego nie jest możliwe zakodowanie przy użyciu kodu binarnego mniejszego niż bity i odzyskanie go z oczekiwanym błędem średniokwadratowym mniejszym niż . Z drugiej strony, dla każdego , istnieje wystarczająco duży i binarny kod składający się z nie więcej niż odrębnych elementów, tak że oczekiwany błąd średniokwadratowy w odzyskiwaniu z tego kodu wynosi co najwyżej . ${\ Displaystyle S (\ varphi ) = \ lewo (2 \ grzech (\ pi \ varphi / 2) \ prawo) ^ {-2}}$${\ Displaystyle {\ {Z_ {n} \} _ {n = 1} ^ {N}}}$${\ Displaystyle NR (D_ {\ theta})}$ ${\displaystyle D_{\theta}}$${\ Displaystyle \ varepsilon > 0}$${\ Displaystyle N \ w \ mathbb {N}}$${\ Displaystyle 2 ^ {NR (D_ {\ theta})}}$${\ Displaystyle {\ {Z_ {n} \} _ {n = 1} ^ {N}}}$${\displaystyle D_{\theta}-\varepsilon}$

Aplikacje

Antony Gormley „s Quantum Chmura rzeźba w Londynie został zaprojektowany przez komputer przy użyciu algorytmu spacer losowy.

Jak wspomniano, zakres zjawisk przyrodniczych, które zostały poddane próbom opisu przez jakiś rodzaj spacerów przypadkowych, jest znaczny, w szczególności w fizyce i chemii, materiałoznawstwie , biologii i różnych innych dziedzinach. Oto kilka konkretnych zastosowań błądzenia losowego:

• W ekonomii finansowej „ hipoteza błądzenia losowego ” jest używana do modelowania cen akcji i innych czynników. Badania empiryczne wykazały pewne odchylenia od tego modelu teoretycznego, zwłaszcza w korelacjach krótko- i długookresowych. Zobacz ceny akcji .
• W genetyce populacyjnej błądzenie losowe opisuje statystyczne właściwości dryfu genetycznego
• W fizyce losowe spacery stosuje uproszczonych modeli fizycznej Browna i dyfuzję, takie jak losowe ruchu z cząsteczek w cieczy i gazów. Zobacz na przykład agregacja ograniczona dyfuzją . Również w fizyce spacery losowe i niektóre spacery samooddziałujące odgrywają rolę w kwantowej teorii pola .
• W ekologii matematycznej spacery losowe są wykorzystywane do opisu ruchów poszczególnych zwierząt, do empirycznego wspomagania procesów biodyfuzji , a czasami do modelowania dynamiki populacji .
• W fizyce polimerów błądzenie losowe opisuje idealny łańcuch . Jest to najprostszy model do badania polimerów .
• W innych dziedzinach matematyki błądzenie losowe jest używane do obliczania rozwiązań równania Laplace'a , do szacowania miary harmonicznej oraz do różnych konstrukcji w analizie i kombinatoryce .
• W informatyce do szacowania rozmiaru sieci wykorzystuje się spacery losowe .
• W segmentacji obrazu spacery losowe są używane do określenia etykiet (tj. „obiektu” lub „tła”), które mają być powiązane z każdym pikselem. Algorytm ten jest zwykle określany jako algorytm segmentacji wędrowca losowego .

We wszystkich tych przypadkach błądzenie losowe jest często zastępowane ruchem Browna.

• W badaniach nad mózgiem spacery losowe i wzmocnione spacery losowe są wykorzystywane do modelowania kaskad wyładowań neuronowych w mózgu.
• W nauce o wzroku dryf oczu ma tendencję do zachowywania się jak błądzenie losowe. Według niektórych autorów ruchy fiksacyjne gałek ocznych w ogóle dobrze opisuje również błądzenie losowe.
• W psychologii spacery losowe dokładnie wyjaśniają związek między czasem potrzebnym na podjęcie decyzji a prawdopodobieństwem podjęcia określonej decyzji.
• Losowe spacery można wykorzystać do pobierania próbek z przestrzeni stanów, która jest nieznana lub bardzo duża, na przykład do wybrania losowej strony z Internetu lub, do badania warunków pracy, losowego pracownika w danym kraju.

• Kiedy to ostatnie podejście jest stosowane w informatyce , jest znane jako łańcuch Markowa Monte Carlo lub w skrócie MCMC. Często próbkowanie z jakiejś skomplikowanej przestrzeni stanów pozwala również uzyskać probabilistyczne oszacowanie wielkości tej przestrzeni. Oszacowanie stałej dużej macierzy zer i jedynek było pierwszym poważnym problemem rozwiązanym przy użyciu tego podejścia.

• Losowe spacery były również wykorzystywane do próbkowania ogromnych wykresów online, takich jak serwisy społecznościowe .
• W sieciach bezprzewodowych spacer losowy jest używany do modelowania ruchu węzła.
• Ruchliwe bakterie angażują się w stronniczy błądzenie losowe .
• Losowe spacery są wykorzystywane do modelowania hazardu .
• W fizyce spacery losowe leżą u podstaw metody estymacji Fermiego .
• W sieci witryna Twitter wykorzystuje przypadkowe spacery, aby zasugerować, kogo należy obserwować
• Dave Bayer i Persi Diaconis udowodnili, że 7 przetasowań karabinów wystarczy, aby wymieszać talię kart (więcej szczegółów w części tasowanie ). Wynik ten przekłada się na stwierdzenie o losowym błądzeniu po grupie symetrycznej, co udowadniają, z istotnym wykorzystaniem struktury grupy poprzez analizę Fouriera.

Warianty

Rozważono szereg typów procesów stochastycznych, które są podobne do czystych błądzeń losowych, ale gdzie prosta struktura może być bardziej uogólniona. Czysta struktura może być scharakteryzowana przez etapów jest określony przez niezależne i jednakowo rozłożonych zmiennych losowych .

Na wykresach

Losowy spacer o długości k na możliwie nieskończonym grafie G z pierwiastkiem 0 jest procesem stochastycznym ze zmiennymi losowymi takimi, że i jest wierzchołkiem wybieranym jednolicie losowo spośród sąsiadów . Wtedy liczba jest prawdopodobieństwem, że błądzenie losowe o długości k rozpoczynające się od v kończy się na w . W szczególności, jeśli G jest grafem z pierwiastkiem 0 , jest to prawdopodobieństwo, że krokowe błądzenie losowe powróci do 0 . ${\displaystyle X_{1},X_{2},\kropki,X_{k}}$${\displaystyle X_{1}=0}$${\ Displaystyle {X_ {i + 1}}}$${\ Displaystyle X_ {i}}$${\ Displaystyle p_ {v, w, k} (G)}$${\displaystyle p_{0,0,2k}}$${\displaystyle 2k}$

Opierając się na analogii z wcześniejszej części o wyższych wymiarach, załóżmy teraz, że nasze miasto nie jest już idealną siatką kwadratową. Kiedy nasza osoba dotrze do pewnego skrzyżowania, z równym prawdopodobieństwem wybiera między różnymi dostępnymi drogami. Tak więc, jeśli skrzyżowanie ma siedem wyjść, osoba przejdzie do każdego z prawdopodobieństwem jeden siódmy. To jest błądzenie losowe na wykresie. Czy nasza osoba dotrze do swojego domu? Okazuje się, że w dość łagodnych warunkach odpowiedź nadal brzmi tak, ale w zależności od wykresu odpowiedź na pytanie wariantowe „Czy dwie osoby spotkają się ponownie?”. nie może być tak, że spotykają się nieskończenie często, prawie na pewno.

Przykładem przypadku, gdy dana osoba osiągnie swój dom prawie na pewno jest, gdy długość wszystkich bloków są między i B (gdzie i b są jakieś dwa skończonymi liczbami dodatnimi). Zauważ, że nie zakładamy, że wykres jest planarny , tzn. miasto może zawierać tunele i mosty. Jednym ze sposobów udowodnienia tego wyniku jest wykorzystanie połączenia z sieciami elektrycznymi . Weź mapę miasta i umieść rezystor 1 om na każdym bloku. Teraz zmierz „opór między punktem a nieskończonością”. Innymi słowy, wybierzmy jakąś liczbę R i weź wszystkie punkty sieci elektrycznej w odległości większej niż R od naszego punktu i połącz je ze sobą. To jest teraz skończona sieć elektryczna i możemy zmierzyć opór od naszego punktu do punktów okablowanych. Zabierz R do nieskończoności. Granica nazywana jest oporem między punktem a nieskończonością . Okazuje się, że prawdą jest co następuje (elementarny dowód można znaleźć w książce Doyle'a i Snella):

Twierdzenie : wykres jest przejściowy wtedy i tylko wtedy, gdy opór między punktem a nieskończonością jest skończony. Nie jest ważne, który punkt zostanie wybrany, jeśli wykres jest połączony.

Innymi słowy, w systemie przejściowym wystarczy pokonać skończony opór, aby dostać się do nieskończoności z dowolnego punktu. W systemie powtarzalnym opór z dowolnego punktu do nieskończoności jest nieskończony.

Ta charakterystyka przemijania i powtarzalności jest bardzo użyteczna, aw szczególności pozwala nam przeanalizować przypadek miasta narysowanego na płaszczyźnie z ograniczonymi odległościami.

Błądzenie losowe na wykresie jest bardzo szczególnym przypadkiem łańcucha Markowa . W przeciwieństwie do ogólnego łańcucha Markowa, błądzenie losowe na wykresie ma właściwość zwaną symetrią czasową lub odwracalnością . Z grubsza rzecz biorąc, własność ta, zwana również zasadą równowagi szczegółowej , oznacza, że ​​prawdopodobieństwa przejścia danej ścieżki w jednym lub drugim kierunku mają między sobą bardzo prosty związek (jeśli graf jest regularny , są po prostu równe). Ta właściwość ma ważne konsekwencje.

Począwszy od lat 80. przeprowadzono wiele badań nad łączeniem właściwości grafu z błądzeniem losowym. Oprócz opisanego powyżej połączenia sieci elektrycznej istnieją ważne powiązania z nierównościami izoperymetrycznymi , czytaj więcej tutaj , nierówności funkcjonalne takie jak nierówności Sobolewa i Poincarégo oraz własności rozwiązań równania Laplace'a . Znaczna część tych badań koncentrowała się na Cayley wykresach z grup skończenie generowanych . W wielu przypadkach te dyskretne wyniki przenoszą się lub pochodzą z rozmaitości i grup Liego .

W kontekście grafów losowych , w szczególności modelu Erdősa–Rényiego , uzyskano wyniki analityczne niektórych właściwości spacerowiczów losowych. Obejmują one rozkład czasu pierwszego i ostatniego uderzenia szwendacza, przy czym pierwszy czas uderzenia jest podawany przy pierwszym wejściu szwendacza do wcześniej odwiedzonej strony wykresu, a czas ostatniego uderzenia odpowiada pierwszemu momentowi, w którym szwendacz nie może wykonać dodatkowy ruch bez ponownego odwiedzania wcześniej odwiedzanej witryny.

Dobrym punktem odniesienia dla błądzenia losowego na wykresach jest internetowa książka autorstwa Aldousa i Filla . Dla grup patrz Księga Woess. Jeśli jądro przejścia jest samo w sobie losowe (w oparciu o środowisko ), to błądzenie losowe nazywa się "losowym chodzeniem w losowym środowisku". Gdy prawo błądzenia losowego obejmuje losowość , prawo to nazywa się prawem wyżarzonym; z drugiej strony, jeśli jest postrzegane jako ustalone, prawo nazywa się prawem zgaszonym. Zobacz księgę Hughesa, księgę Revesza lub notatki z wykładów Zeitouni. ${\displaystyle p(x,y)}$${\ Displaystyle \ omega}$${\ Displaystyle \ omega}$${\ Displaystyle \ omega}$

Możemy myśleć o wyborze każdej możliwej krawędzi z takim samym prawdopodobieństwem jak lokalna maksymalizacja niepewności (entropii). Moglibyśmy to również zrobić globalnie – w przypadku błądzenia losowego o maksymalnej entropii (MERW) chcemy, aby wszystkie ścieżki były jednakowo prawdopodobne, czyli innymi słowy: dla każdych dwóch wierzchołków każda ścieżka o danej długości jest jednakowo prawdopodobna. Ten błądzenie losowe ma znacznie silniejsze właściwości lokalizacyjne.

Interakcyjne losowe spacery

Istnieje wiele ciekawych modeli losowych ścieżek, w których każdy krok w skomplikowany sposób zależy od przeszłości. Wszystkie są bardziej złożone do rozwiązania analitycznego niż zwykłe błądzenie losowe; jednak zachowanie dowolnego modelu losowego piechura jest możliwe do uzyskania przy użyciu komputerów. Przykłady obejmują:

• Self-unikanie odległości .

Self-unikanie odległości od długości n na to losowa n -step ścieżka, która rozpoczyna się na początku, tylko sprawia, że przejścia między sąsiednimi witrynach , nigdy ponownie witryny i dobiera się równomiernie wśród wszystkich takich ścieżek. W dwóch wymiarach, ze względu na samo-pułapki, typowy samounikający spacer jest bardzo krótki, podczas gdy w wyższym wymiarze rozrasta się poza wszelkie granice. Model ten był często stosowany w fizyce polimerów (od lat 60. XX wieku). ${\ Displaystyle \ mathbb {Z} ^ {d}}$${\ Displaystyle \ mathbb {Z} ^ {d}}$

• Błądzenia losowego pętli skasowane .
• Wzmocnioną losowych walk .
• Proces eksploracji .
• Wieloagentowym błądzenia losowego .

Skorelowane spacery dalekiego zasięgu

Długozasięgowe skorelowane szeregi czasowe występują w wielu systemach biologicznych, klimatologicznych i ekonomicznych.

• Rekordy bicia serca
• Niekodujące sekwencje DNA
• Szeregi czasowe zmienności akcji
• Zapisy temperatury na całym świecie

Stronnicze spacery losowe na wykresach

Maksymalna entropia błądzenie losowe

Chodzenie losowe wybrane w celu maksymalizacji szybkości entropii , ma znacznie silniejsze właściwości lokalizacyjne.

Skorelowane przypadkowe spacery

Spacery losowe, w których kierunek ruchu w jednym czasie jest skorelowany z kierunkiem ruchu w następnym czasie. Służy do modelowania ruchów zwierząt.

Zobacz też

• Rozgałęzione spacerowanie losowe
• Ruch Browna
• Prawo iterowanego logarytmu
• Lot Lévy'ego
• Hipoteza Lévy'ego dotycząca poszukiwania pożywienia
• Losowe chodzenie z zapętleniem
• Maksymalna entropia błądzenie losowe
• Samounikający spacer
• Jednostka główna

Bibliografia

Bibliografia

• Aldous, Dawid ; Wypełnij, James Allen (2002). Odwracalne łańcuchy Markowa i losowe spacery na wykresach . Zarchiwizowane z oryginału w dniu 27 lutego 2019 r.
• Ben-Awraham D.; Havlin S. , Diffusion and Reactions in Fractal and Disordered Systems , Cambridge University Press, 2000.
• Doyle, Peter G.; Snell, J. Laurie (1984). Spacery losowe i sieci elektryczne . Monografie matematyczne Carusa. 22 . Amerykańskie Stowarzyszenie Matematyczne . arXiv : math.PR/0001057 . Numer ISBN 978-0-88385-024-4. MR  0920811 .
• Feller, William (1968), Wprowadzenie do teorii prawdopodobieństwa i jej zastosowań (tom 1). ISBN  0-471-25708-7
• Hughes, Barry D. (1996), Random Walks and Random Environments , Oxford University Press. ISBN  0-19-853789-1
• Norris, James (1998), Łańcuchy Markowa , Cambridge University Press. ISBN  0-521-63396-6
• Pólya G. (1921), „Über eine Aufgabe der Wahrscheinlichkeitsrechnung betreffend die Irrfahrt im Strassennetz” , Mathematische Annalen , 84 (1–2): 149–160, marzec 1921.
• Révész, Pal (2013), Random Walk w środowiskach losowych i nielosowych (wydanie trzecie) , World Scientific Pub Co. ISBN  978-981-4447-50-8
• Sunada, Toshikazu (2012). Krystalografia topologiczna: z myślą o dyskretnej analizie geometrycznej . Ankiety i samouczki w stosowanych naukach matematycznych. 6 . Skoczek. Numer ISBN 978-4-431-54177-6.
• Weiss G. Aspects and Applications of the Random Walk , North-Holland, 1994.
• Woess, Wolfgang (2000), Random Walks on Infinite Graphs and Groups , trakty Cambridge w matematyce 138, Cambridge University Press. ISBN  0-521-55292-3

Zewnętrzne linki

• Stałe losowego spaceru Pólyi
• Losowy spacer w aplecie Java
• Kwantowy błądzenie losowe
• Estymator błądzenia losowego Gaussa
• Modele przewodnictwa elektronowego z wykorzystaniem maksymalnej entropii Losowe spacery Projekt demonstracyjny Wolframa