Twierdzenie Schrödera-Bernsteina - Schröder–Bernstein theorem

W teorii zbiorów The Schroeder-Bernsteina wskazuje, że jeśli istnieją funkcje injective f  : A → B i g  : B → A między zestawami A i B , to istnieje bijective funkcji h  : A → B .

Z punktu widzenia liczności tych dwóch zbiorów, klasycznie implikuje to, że jeśli | | ≤ | B | i | B | ≤ | | , to | | = | B | ; to znaczy, A i B są równoważne . Jest to przydatna funkcja przy porządkowaniu liczb głównych .

Twierdzenie nosi imię Felixa Bernsteina i Ernsta Schrödera . Jest również znany jako twierdzenie Cantora-Bernsteina lub Cantora-Schrödera-Bernsteina , od Georga Cantora, który jako pierwszy opublikował je bez dowodu.

Dowód

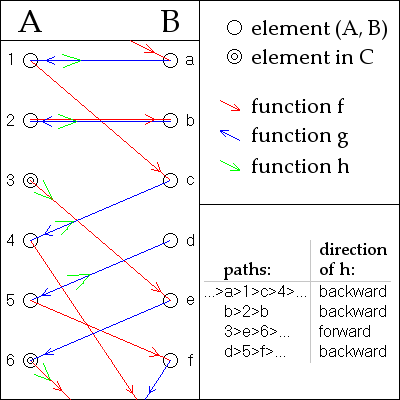
Definicja Königa bijekcji h : A  →  B z podanych przykładów iniekcji f : A  →  B i g : B  →  A . Element w A i B jest oznaczony odpowiednio liczbą i literą. Ciąg 3 → e → 6 → ... jest stoperem A , prowadzącym do definicji h (3) =  f (3) =  e , h (6) =  f (6), .... Ciąg d  → 5 →  f  → ... to korek B , prowadzący do h (5) =  g −1 (5) =  d , .... Sekwencja ... →  a  → 1 →  c  → 4 → .. jest podwójnie nieskończony, co prowadzi do h (1) =  g -1 (1) =  a , h (4) =  g -1 (4) =  c , .... Sekwencja b  → 2 →  b jest cykliczna, prowadząca do h (2) =  g -1 (2) =  b .

Poniższy dowód przypisywany jest Juliusowi Königowi .

Załóżmy bez utraty ogólności , że A i B są rozłączne . Dla dowolnego a w A lub b w B możemy utworzyć unikalną dwustronną sekwencję elementów, które są naprzemiennie w A i B , przez wielokrotne stosowanie i przejście od A do B oraz i przejście od B do A (gdzie zdefiniowano; odwrotności i są rozumiane jako funkcje cząstkowe na tym etapie dowodu.)

Dla każdego konkretnego a sekwencja ta może kończyć się w lewo lub nie, w punkcie, w którym lub nie jest zdefiniowana.

Przez fakt, że i są funkcjami iniektywnymi, każda a w A i b w B jest w dokładnie jednej takiej sekwencji w ramach identyczności: jeśli element występuje w dwóch sekwencjach, wszystkie elementy po lewej i po prawej stronie muszą być takie same w obu , przez definicję sekwencji. Dlatego sekwencje tworzą podział (rozłącznej) unii A i B . Wystarczy więc wytworzyć bijekcję między elementami A i B w każdej z sekwencji oddzielnie, jak następuje:

Nazwij sekwencję A-stopperem, jeśli zatrzyma się na elemencie A , lub B-stopperem, jeśli zatrzyma się na elemencie B . W przeciwnym razie nazwij to podwójnie nieskończonym, jeśli wszystkie elementy są różne lub cykliczne, jeśli się powtarza. Zobacz przykładowe zdjęcie.

  • W przypadku A-stopper , funkcja jest bijekcją między jej elementami w A i jej elementami w B .
  • W przypadku B-stopper , funkcja jest bijekcją między jej elementami w B i jej elementami w A .
  • W przypadku sekwencji podwójnie nieskończonej lub sekwencji cyklicznej albo lub zrobi to ( na rysunku użyto ).

Historia

Tradycyjna nazwa „Schröder-Bernstein” opiera się na dwóch dowodach opublikowanych niezależnie w 1898 r. Często dodaje się kantora, ponieważ po raz pierwszy wypowiedział twierdzenie w 1887 r., podczas gdy nazwisko Schrödera jest często pomijane, ponieważ jego dowód okazał się błędny, podczas gdy nazwisko Richarda Dedekind , który to pierwszy udowodnił, nie jest związany z twierdzeniem. Według Bernsteina Cantor zaproponował twierdzenie o równoważności nazwy (Ęquivalenzsatz).

Pierwsze stwierdzenie Cantora z twierdzenia (1887)
  • 1887 Cantor publikuje twierdzenie, jednak bez dowodu.
  • 1887 11 lipca Dedekind udowadnia twierdzenie (nie powołując się na aksjomat wyboru ), ale ani nie publikuje swojego dowodu, ani nie opowiada o nim Cantorowi. Ernst Zermelo odkrył dowód Dedekinda iw 1908 publikuje swój własny dowód oparty na teorii łańcuchów z pracy Dedekinda Was sind und was sollen die Zahlen?
  • 1895 Cantor podaje twierdzenie w swoim pierwszym artykule o teorii mnogości i liczbach nieskończonych. Uzyskuje ją jako łatwą konsekwencję liniowego porządku liczb kardynalnych. Jednak nie mógł dowieść tego ostatniego twierdzenia, który jest pokazany w 1915 roku będzie równoznaczne z aksjomatu wyboru przez Friedrich Moritz Hartogs .
  • 1896 Schröder ogłasza dowód (jako wniosek twierdzenia Jevonsa ).
  • 1897 Bernstein , 19-letni student Seminarium Kantora, przedstawia swój dowód.
  • 1897 Niemal jednocześnie, ale niezależnie Schröder znajduje dowód.
  • 1897 Po wizycie Bernsteina Dedekind samodzielnie udowadnia to twierdzenie po raz drugi.
  • 1898 Dowód Bernsteina (nie opierający się na aksjomacie wyboru) publikuje Émile Borel w swojej książce o funkcjach. (Komunikowane przez Cantora na Międzynarodowym Kongresie Matematyków w Zurychu w 1897 r .) W tym samym roku dowód pojawia się również w rozprawie Bernsteina .
  • 1898 Schröder publikuje swój dowód, który jednak okazuje się wadliwy przez Alwina Reinholda Korselta w 1902 r. (tuż przed śmiercią Schrödera), (potwierdzony przez Schrödera), ale artykuł Korselta ukazuje się dopiero w 1911 r.

Oba dowody Dedekinda oparte są na jego słynnych wspomnieniach z 1888 roku Was sind und was sollen die Zahlen? i wyprowadź to jako następstwo zdania równoważnego stwierdzeniu C w pracy Cantora, które brzmi A  ⊆  B  ⊆  C i | | = | C | implikuje | | = | B | = | C |. Cantor zaobserwował tę właściwość już w latach 1882/83 podczas swoich studiów nad teorią mnogości i liczbami nieskończonymi i dlatego (domyślnie) opierał się na Aksjomat wyboru .

Warunki wstępne

Dowód Cantora z 1895 r. opierał się w rzeczywistości na aksjomacie wyboru , wnioskując wynik jako następstwo twierdzenia o dobrym porządku . Jednak dowód Königa podany powyżej pokazuje, że wynik można również udowodnić bez użycia aksjomatu wyboru.

Z drugiej strony, dowód Königa wykorzystuje zasadę wyłączonego środka , aby przeprowadzić analizę w przypadkach, więc dowód ten nie działa w konstruktywnej teorii mnogości . Co więcej, żaden dowód nie może w ogóle istnieć z samej konstruktywnej teorii mnogości (tzn. rezygnując z zasady wyłączonego środka), ponieważ twierdzenie Schrödera-Bernsteina implikuje zasadę wyłączonego środka. Dlatego intuicjoniści nie akceptują twierdzenia.

Istnieje również dowód wykorzystujący twierdzenie Tarskiego o punkcie stałym .

Zobacz też

Uwagi

Bibliografia

Zewnętrzne linki