Trisekcja kąta - Angle trisection

Trisekcja kątów jest klasycznym problemem budowy linii prostej i cyrkla w starożytnej matematyce greckiej . Chodzi o konstruowanie kąta równego jednej trzeciej dowolnego kąta, przy użyciu tylko dwóch narzędzi: nieoznaczonej linijki i cyrkla .

Pierre Wantzel udowodnił w 1837 roku, że problem, jak stwierdzono, jest niemożliwy do rozwiązania dla dowolnych kątów. Jednakże, chociaż ogólnie nie ma możliwości rozcięcia kąta za pomocą tylko kompasu i linijki, można dokonać tria niektórych specjalnych kątów. Na przykład stosunkowo łatwo jest przeciąć pod kątem prostym (to znaczy skonstruować kąt miary 30 stopni).

Możliwe jest trisekcję dowolnego kąta za pomocą narzędzi innych niż liniał i cyrkla. Na przykład konstrukcja neusis , znana również starożytnym Grekom, polega na jednoczesnym przesuwaniu i obracaniu zaznaczonej liniału , czego nie można osiągnąć za pomocą oryginalnych narzędzi. Inne techniki zostały opracowane przez matematyków na przestrzeni wieków.

Ponieważ jest definiowany w sposób prosty, ale złożony, by okazać się nierozwiązywalny, problem trisekcji kątów jest częstym przedmiotem pseudomatematycznych prób rozwiązania przez naiwnych entuzjastów. Te „rozwiązania” często wiążą się z błędną interpretacją przepisów lub są po prostu błędne.

Tło i opis problemu

Stosując tylko nieoznaczoną liniał i kompas, grecki matematyków znaleźć środki, aby podzielić linię do dowolnego zestawu równych segmentów zwrócić równoległych linii, aby Przepoławiana kątami , aby skonstruować wiele wielokątów oraz konstruować kwadraty lub równy dwukrotnej powierzchni danego wielokąta.

Nieuchwytne okazały się trzy problemy, a mianowicie podzielenie kąta na trzy części, podwojenie sześcianu i kwadratura koła . Problem trisekcji kątowej brzmi:

Skonstruuj kąt równy jednej trzeciej podanego dowolnego kąta (lub podziel go na trzy równe kąty), używając tylko dwóch narzędzi:

1. nieoznaczona liniał i
2. kompas.

Dowód niemożliwości

Pierre Wantzel opublikował w 1837 r. dowód niemożności klasycznego przecięcia dowolnego kąta. Dowód Wantzela, powtórzony we współczesnej terminologii, wykorzystuje koncepcję rozszerzeń pola , temat obecnie zwykle łączony z teorią Galois . Jednak Wantzel opublikował te wyniki wcześniej niż Évariste Galois (którego dzieło, napisane w 1830 r., ukazało się dopiero w 1846 r.) i nie korzystał z wprowadzonych przez Galois pojęć.

Problem skonstruowania kąta o danej miary θ jest równoważny konstrukcji dwóch odcinków w taki sposób, że stosunek ich długości wynosi cos  θ . Od rozwiązania jednego z tych dwóch problemów można przejść do rozwiązania drugiego za pomocą konstrukcji cyrkla i liniału. Wzór potrójnego kąta daje ekspresję odnoszące cosinusami pierwotnego kąta, a jej Trysekcja: cos  θ  =  4 bo ³ θ/3 − 3 cos θ/3.

Wynika z tego, że dla danego odcinka, który jest zdefiniowany jako jednostka długości, problem trisekcji kąta jest równoważny konstruowaniu odcinka, którego długość jest pierwiastkiem wielomianu sześciennego . Ta równoważność redukuje pierwotny problem geometryczny do problemu czysto algebraicznego.

Każda liczba wymierna jest możliwa do zbudowania. Każda liczba niewymierna, którą można skonstruować w jednym kroku z danych liczb, jest pierwiastkiem wielomianu stopnia 2 ze współczynnikami w polu generowanym przez te liczby. Dlatego każda liczba, którą można skonstruować przez sekwencję kroków, jest pierwiastkiem minimalnego wielomianu, którego stopień jest potęgą dwójki . Kątπ/3 radiany (60 stopni , zapisane 60°) są możliwe do zbudowania . Poniższy argument pokazuje, że nie da się skonstruować kąta 20°. Oznacza to, że kąt 60° nie może zostać poddany trisekcji, a zatem dowolny kąt nie może zostać poddany trisekcji.

Oznaczmy zbiór liczb wymiernych przez Q . Gdyby 60° można było podzielić na trzy części, stopień minimalnego wielomianu cos 20° przez Q byłby potęgą dwójki. Teraz niech x = cos 20° . Zauważ, że cos 60° = cosπ/3 = 1/2. Następnie według wzoru potrójnego kąta, cosπ/3= 4 x ³ − 3 x i tak 4 x ³ − 3 x =1/2. Zatem 8 x ³ − 6 x − 1 = 0 . Zdefiniuj p ( t ) jako wielomian p ( t ) = 8 t ³ − 6 t − 1 .

Ponieważ x = cos 20° jest pierwiastkiem p ( t ) , minimalny wielomian dla cos 20° jest współczynnikiem p ( t ) . Ponieważ p ( t ) ma stopień 3, jeśli jest redukowalne przez Q, to ma pierwiastek wymierny . Według twierdzenia o racjonalnym pierwiastku pierwiastek ten musi wynosić ±1, ±1/2, ±1/4lub ±1/8, ale żaden z nich nie jest korzeniem. Dlatego p ( t ) jest nieredukowalne przez Q , a minimalny wielomian dla cos 20° ma stopień  3 .

Zatem kąt miary 60° nie może być rozdzielony.

Kąty, które można podzielić na trzy części

Jednak niektóre kąty można podzielić na trzy części. Na przykład, dla każdej konstruowalnych kąt θ , kąt środka 3 θ można trywialny na trzy części, pomijając danym kącie i jest bezpośrednio konstruowania kąt środka θ . Istnieją kąty, których nie da się zbudować, ale są trójdzielne (pomimo, że jedna trzecia samego kąta jest nie do zbudowania). Na przykład,3 π/7 czy taki kąt: pięć kątów miary 3 π/7 połącz, aby uzyskać kąt miary 15 π/7, czyli pełne koło plus pożądane π/7.

Dla dodatniej liczby całkowitej N , kąt miary2 π/njest trójdzielna wtedy i tylko wtedy, gdy 3 nie dzieli N . W przeciwieństwie,2 π/njest konstruowalny wtedy i tylko wtedy, gdy N jest potęgą 2 lub iloczynem potęgi 2 z iloczynem jednej lub więcej różnych liczb pierwszych Fermata .

Charakterystyka algebraiczna

Ponownie oznaczmy zbiór liczb wymiernych przez Q .

Twierdzenie : Kąt miary θ może być triscięty wtedy i tylko wtedy, gdy q ( t ) = 4 t ³ − 3 t − cos( θ ) jest redukowalne na rozszerzeniu pola Q (cos( θ ) ) .

Dowodem jest stosunkowo proste uogólnienie dowodu, że dany powyżej 60 ° kąt nie trisectible.

Inne metody

Ogólny problem trisekcji kątów można rozwiązać za pomocą dodatkowych narzędzi, a tym samym wychodząc poza oryginalne greckie ramy cyrkla i linijki.

Zaproponowano wiele błędnych metod trysekcji kąta ogólnego. Niektóre z tych metod zapewniają rozsądne przybliżenia; inne (niektóre z nich są wymienione poniżej) obejmują narzędzia niedozwolone w klasycznym problemie. Matematyk Underwood Dudley szczegółowo opisał niektóre z tych nieudanych prób w swojej książce The Trisectors .

Aproksymacja przez kolejne bisekcje

Trisekcja może być aproksymowana przez powtórzenie metody cyrkla i linijki dla dwusiecznej kąta. Seria geometryczna1/3 = 1/4 + 1/16 + 1/64 + 1/256+ ⋯ lub1/3 = 1/2 − 1/4 + 1/8 − 1/16+ ⋯ może być wykorzystany jako podstawa dla dwusekcji. Przybliżenie o dowolnym stopniu dokładności można uzyskać w skończonej liczbie kroków.

Korzystanie z origami

Trisekcja, podobnie jak wiele konstrukcji niemożliwych za pomocą linijki i cyrkla, może być łatwo wykonana za pomocą operacji składania papieru lub origami . Aksjomaty Huzity (rodzaje operacji składania) mogą konstruować rozszerzenia sześcienne (pierwiastki sześcienne) o określonych długościach, podczas gdy linijka i kompas mogą konstruować tylko rozszerzenia kwadratowe (pierwiastki kwadratowe).

Korzystanie z powiązania

Istnieje wiele prostych połączeń, które można wykorzystać do wykonania instrumentu do trisektowania kątów, w tym Trisector Kempe'a i Sylvester's Link Fan lub Isoklinostat.

Z prawą trójkątną linijką

W 1932 roku Ludwig Bieberbach opublikował w Journal für die reine und angewandte Mathematik swoją pracę Zur Lehre von den kubischen Konstruktionen . Stwierdza w nim (tłumaczenie bezpłatne):

" Jak wiadomo ... każdy sześcienny konstrukcja może być wstecz do Trysekcja kąta i do mnożenia sześcianu, czyli ekstrakcja trzeciego korzenia. Muszę tylko pokazać, jak te dwa klasyczne zadania mogą być rozwiązany za pomocą haka pod kątem prostym. ”

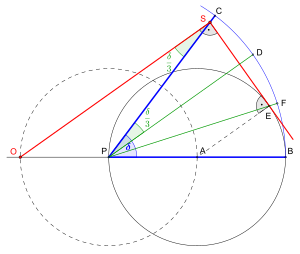
Konstrukcję rozpoczynamy od narysowania okręgu przechodzącego przez wierzchołek P kąta, który ma być przecięty, wyśrodkowany w punkcie A na krawędzi tego kąta i mający B jako drugie przecięcie z krawędzią. Okrąg o środku w punkcie P i o tym samym promieniu przecina linię wspierającą krawędź w A i O .

Teraz prawą linijkę trójkątną umieszczamy na rysunku w następujący sposób: jedna noga jej kąta prostego przechodzi przez O ; wierzchołek jej kąta prostego jest umieszczony w punkcie S na prostej PC w taki sposób, że druga noga linijki jest styczna w punkcie E do okręgu o środku w punkcie A . Wynika z tego, że pierwotny kąt jest przecinany przez prostą PE i prostą PD prostopadłą do SE i przechodzącą przez P . Tę linię można narysować albo ponownie używając prawej trójkątnej linijki, albo stosując tradycyjną konstrukcję linijki i cyrkla . Przy podobnej konstrukcji można poprawić położenie E , używając tego, że jest to przecięcie prostej SE i jej prostopadłej przechodzącej przez A .

Dowód: Jeden ma udowodnić równości kątów i Trzy linie OS , PD i AE są równoległe. Ponieważ odcinki OP i PA są równe, te trzy równoległe linie wyznaczają dwa równe odcinki na każdej innej siecznej, aw szczególności na ich wspólnej prostopadłej SE . Zatem SD ' = D ' E , gdzie D ' jest przecięciem prostych PD i SE . Wynika stąd, że trójkątami PD „ S i PD ” E są przystające, a tym samym, że pierwszy żądany równości. Z drugiej strony trójkąt PAE jest równoramienny , ponieważ wszystkie promienie koła są równe; oznacza to, że ma również, ponieważ te dwa kąty są naprzemiennymi kątami poprzecznej do dwóch równoległych linii. Dowodzi to drugiej pożądanej równości, a tym samym poprawności konstrukcji. ${\displaystyle {\widehat {EPD}}={\widehat {DPS}}}$${\ Displaystyle {\ widehat {BPE}} = {\ widehat {EPD}}.}$ ${\displaystyle {\widehat {EPD}}={\widehat {DPS}}}$${\ Displaystyle {\ widehat {APE}} = {\ widehat {AEP}}.}$${\displaystyle {\widehat {AEP}}={\widehat {EPD}}}$

Z krzywą pomocniczą

• 

  Trysekcja za pomocą spirali Archimedesa

• 

  Trisekcja za pomocą Maclaurina trisectrix

Istnieją pewne krzywe zwane trisectrics, które po narysowaniu na płaszczyźnie innymi metodami można wykorzystać do przecięcia dowolnych kątów. Przykłady obejmują trisectrix Colina Maclaurina , podaną we współrzędnych kartezjańskich przez niejawne równanie

${\ Displaystyle 2x (x ^ {2} + y ^ {2}) = a (3x ^ {2}-y ^ {2})}$

i spirala Archimedesa . Spiralę można w rzeczywistości wykorzystać do podzielenia kąta na dowolną liczbę równych części.

Z zaznaczoną linijką

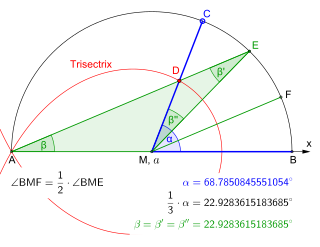
Innym sposobem na przecięcie dowolnego kąta przez „mały” krok poza grecką ramę jest użycie linijki z dwoma znakami w określonej odległości. Kolejna konstrukcja pochodzi ze względu na Archimedesa , zwany budowa Neusis , czyli narzędzia, które wykorzystuje inne niż un oznakowane liniału. Diagramy, których używamy, pokazują tę konstrukcję dla kąta ostrego, ale rzeczywiście działa ona dla każdego kąta do 180 stopni.

Wymaga to trzech faktów z geometrii (po prawej):

1. Dowolny pełny zestaw kątów na linii prostej dodaje się do 180°,
2. Suma kątów dowolnego trójkąta wynosi 180 °, a ,
3. Dowolne dwa równe boki z trójkąta równoramiennego będzie spełniać trzeci pod takim samym kątem .

Niech l będzie linią poziomą na sąsiednim schemacie. Przedmiotem trisekcji jest kąt a (na lewo od punktu B ). Najpierw punkt A jest rysowany na promieniu kąta , o jedną jednostkę od B . Narysowany zostanie okrąg o promieniu AB . Następnie w grę wchodzi znaczenie linijki: jeden znak linijki umieszcza się w A, a drugi w B . Trzymając linijkę (ale nie znak) dotykając A , linijkę przesuwa się i obraca, aż jeden znak znajdzie się na okręgu, a drugi na linii l . Znak na okręgu jest oznaczony jako C, a znak na linii jest oznaczony jako D . Gwarantuje to, że CD = AB . Narysowany jest promień BC, aby było oczywiste, że odcinki AB , BC i CD mają jednakową długość. Teraz trójkąty ABC i BCD są równoramienne , a zatem (według Faktu 3 powyżej) każdy ma dwa równe kąty.

Hipoteza : dane AD jest linią prostą, a AB , BC i CD mają jednakową długość,

Wniosek : kąt b =a/3.

Dowód :

1. Z Faktu 1) powyżej, °.${\displaystyle e+c=180}$
2. Patrząc na trójkąt BCD , z Faktu 2) °.${\displaystyle e+2b=180}$
3. Z dwóch ostatnich równań .${\displaystyle c=2b}$
4. Z Faktu 2), °, a więc ° , a więc od ostatniego, ° .${\displaystyle d+2c=180}$${\displaystyle d=180}$${\displaystyle -2c}$${\displaystyle d=180}$${\ Displaystyle -4b}$
5. Z Faktu 1) powyżej, °, a więc ° °.${\displaystyle a+d+b=180}$${\displaystyle a+(180}$${\ Displaystyle -4b) + b = 180}$

Clearing, a − 3 b = 0 , lub a = 3 b , a twierdzenie jest udowodnione .

Ponownie, ta konstrukcja wyszedł z ramy z dopuszczalnych konstrukcji za pomocą zaznaczonego szyny.

Ze sznurkiem

Thomas Hutcheson opublikował artykuł w The Mathematics Teacher , w którym zamiast cyrkla i linijki użył sznurka. Sznurek może służyć jako liniał (przez naciągnięcie go) lub cyrkiel (poprzez ustalenie jednego punktu i zidentyfikowanie drugiego), ale można go również owinąć wokół cylindra, klucza do rozwiązania Hutchesona.

Hutcheson skonstruował walec z kąta, który miał zostać podzielony, rysując łuk w poprzek kąta, uzupełniając go w okrąg i konstruując z tego koła walec, na którym, powiedzmy, wpisany był trójkąt równoboczny (kąt 360 stopni podzielony na trzy ). Zostało to następnie „zmapowane” na kąt, który miał zostać podzielony, z prostym dowodem na istnienie podobnych trójkątów.

Z „tomahawkiem”

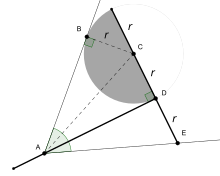
„ Tomahawk ” jest kształtem geometrycznym składającym się z półokręgu i dwóch prostopadłych odcinków linii, tak że długość krótszego odcinka jest równa promieniowi okręgu. Trisekcja jest wykonywana przez oparcie końca krótszego segmentu tomahawka o jeden promień, a krawędź koła o drugi tak, aby „uchwyt” (dłuższy segment) przecinał wierzchołek kąta; linia trisekcji biegnie między wierzchołkiem a środkiem półokręgu.

Chociaż tomahawk można zbudować za pomocą kompasu i linijki, generalnie nie jest możliwe skonstruowanie tomahawka w dowolnej pożądanej pozycji. Zatem powyższa konstrukcja nie zaprzecza nierozdzielności kątów za pomocą samej linijki i cyrkla.

Ponieważ tomahawk może być używany jako ekierka , może być również używany do kątów trisekcji metodą opisaną w § Z linijką trójkątną prawą .

Tomahawk daje taki sam efekt geometryczny jak metoda składania papieru: odległość między środkiem okręgu a końcem krótszego segmentu jest dwukrotnie większa od odległości promienia, co gwarantuje kontakt z kątem. Jest to również równoznaczne z zastosowaniem przez architektów L-Ruler ( plac stolarski ).

Z połączonymi kompasami

Kąt można podzielić na trzy części za pomocą urządzenia, które jest zasadniczo czterozębną wersją kompasu, z połączeniami między zębami zaprojektowanymi tak, aby trzy kąty między sąsiednimi zębami były równe.

Zastosowania trisekcji kątowej

Sześcienny równanie o współczynnikach rzeczywistych może być rozwiązany geometrycznie z kompasu liniału, a trisector kątem, wtedy i tylko wtedy, gdy ma trzy rzeczywiste korzenie .

Regularnego wieloboku o n bokach może być wykonana z linijką, kompas kątowy trisector wtedy i tylko wtedy , gdy R, S, K ≥ 0 i jeżeli P _i są różnymi liczbami pierwszymi większa niż 3 formy (tj Pierpont bodźce większa niż 3 ). ${\ Displaystyle n = 2 ^ {r} 3 ^ {s} p_ {1} p_ {2} \ cdots p_ {k}}$${\ Displaystyle 2 ^ {t} 3 ^ {u} + 1}$

Uogólnienie

Dla dowolnej niezerowej liczby całkowitej N kąt miary 2 π ⁄ N radianów można podzielić na n równych części za pomocą liniału i kompasu wtedy i tylko wtedy, gdy n jest potęgą 2 lub jest potęgą 2 pomnożoną przez iloczyn jednego lub bardziej wyraźne liczby pierwsze Fermata, z których żadna nie dzieli N . W przypadku trisekcji ( n = 3 , która jest liczbą pierwszą Fermata), warunek ten staje się wspomnianym powyżej wymogiem, aby N nie było podzielne przez 3 .

Zobacz też

• Przepołowienie
• Numer do zbudowania
• Konstruowany wielokąt
• Geometria euklidesowa
• Historia geometrii
• Twierdzenie o trisektorach Morleya
• Czworokąt
• Trisectrix
• Kryptografia geometryczna

Bibliografia

Dalsza lektura

• Courant Richard, Herbert Robbins, Ian Stewart, Czym jest matematyka?: elementarne podejście do idei i metod , Oxford University Press US, 1996. ISBN  978-0-19-510519-3 .

Zewnętrzne linki

• Strona MathWorld
• Zagadnienia geometryczne starożytności, w tym trisekcja kątów
• Trochę historii
• Jedno ogniwo zaznaczonej konstrukcji linijki
• Inny, wspominając Archimedesa
• Długi artykuł z wieloma przybliżeniami i oznacza wyjście poza ramy greckie
• Strona geometrii

Inne sposoby trisekcji

• Przybliżony kąt trisekcji jako animacja, max. błąd kąta ≈ ±4E-8°
• Trisecting poprzez ( archiwizowano 2009-10-25) na Ślimak Pascala w Pascal ; zobacz także Trisectrix
• Trisecting poprzez na spirali Archimedesa
• Trisecting poprzez na konchoida z Nicomedes
• Witryna sciencenews.org dotycząca korzystania z origami
• Trisekcja hiperboliczna i widmo wielokątów foremnych