stopień Turinga - Turing degree

W informatyce i logiki matematycznej stopni Turing (nazwa pochodzi od Alana Turinga ) lub stopnia unsolvability zbioru liczb naturalnych mierzy poziom algorytmicznego unsolvability zestawu.

Przegląd

Pojęcie stopnia Turinga jest fundamentalne w teorii obliczalności , gdzie zbiory liczb naturalnych są często traktowane jako problemy decyzyjne . Stopień Turinga zbioru jest miarą trudności rozwiązania problemu decyzyjnego związanego ze zbiorem, to znaczy określenia, czy w danym zbiorze znajduje się dowolna liczba.

Dwa zestawy są równoważne Turingowi, jeśli mają ten sam poziom nierozwiązywalności; każdy stopień Turinga jest zbiorem równoważnych zestawów Turinga, tak że dwa zestawy są w różnych stopniach Turinga dokładnie wtedy, gdy nie są równoważne Turingowi. Co więcej, stopnie Turinga są częściowo uporządkowane tak, że jeśli stopień Turinga zbioru X jest mniejszy niż stopień Turinga zbioru Y, to każda (nieobliczalna) procedura, która poprawnie decyduje, czy liczby są w Y, może być skutecznie przekonwertowana na procedurę, która poprawnie decyduje, czy liczby są w X . W tym sensie stopień Turinga zbioru odpowiada jego poziomowi algorytmicznej nierozwiązywalności.

Stopnie Turinga zostały wprowadzone przez Emila Leona Posta (1944), a wiele fundamentalnych wyników ustalili Stephen Cole Kleene i Post (1954). Stopnie Turinga były od tego czasu przedmiotem intensywnych badań. Wiele dowodów w tej dziedzinie wykorzystuje technikę sprawdzania, znaną jako metoda priorytetu .

Równoważność Turinga

W dalszej części tego artykułu słowo zbiór będzie odnosić się do zbioru liczb naturalnych. Mówi się, że zbiór X jest redukowalny przez Turinga do zbioru Y, jeśli istnieje wyrocznia maszyna Turinga, która decyduje o członkostwie w X, gdy otrzymuje wyrocznię za członkostwo w Y . Notacja X ≤ _T Y wskazuje, że X jest redukowalnym przez Turinga do Y .

Dwa zestawy X i Y są zdefiniowane jako równoważne Turingowi, jeśli X jest Turingiem redukowalnym do Y i Y jest Turingiem redukowalnym do X . Notacja X ≡ _T Y wskazuje, że X i Y są równoważne Turingowi. Relacja ≡ _T może być postrzegana jako relacja równoważności , co oznacza , że dla wszystkich zbiorów X , Y i Z :

• X ≡ _T X
• X ≡ _T Y implikuje Y ≡ _T X
• Jeśli X ≡ _T Y i Y ≡ _T Z to X ≡ _T Z .

Stopień Turing jest klasa równoważności relacji ≡ _T . Oznaczenie [ X ] oznacza klasę równoważności zawierającą zbiór X . Cała kolekcja stopni Turinga jest oznaczona . ${\displaystyle {\mathcal {D}}}$

Stopnie Turinga mają porządek częściowy ≤ zdefiniowany tak, że [ X ] ≤ [ Y ] wtedy i tylko wtedy, gdy X ≤ _T Y . Istnieje unikalny stopień Turinga zawierający wszystkie zbiory obliczalne, a stopień ten jest mniejszy niż każdy inny stopień. Jest oznaczony jako 0 (zero), ponieważ jest to najmniejszy element posetu . (Powszechnie używa się notacji pogrubionej dla stopni Turinga, aby odróżnić je od zestawów. Gdy nie może wystąpić pomyłka, na przykład w przypadku [ X ], pogrubienie nie jest konieczne.) ${\displaystyle {\mathcal {D}}}$

Dla dowolnych zbiorów X i Y , X łączy się z Y, zapisanym X ⊕ Y , jest zdefiniowany jako suma zbiorów {2 n  : n ∈ X } i {2 m +1 : m ∈ Y }. Stopień Turinga X ⊕ Y jest najmniejszą górną granicą stopni X i Y . Tak jest sprzężenie-semilattic . Przynajmniej górna granica stopnia a i b jest oznaczona na ∪ b . Wiadomo, że nie jest to krata , ponieważ istnieją pary stopni bez największego ograniczenia dolnego. ${\displaystyle {\mathcal {D}}}$${\displaystyle {\mathcal {D}}}$

Dla dowolnego zbioru X notacja X ′ oznacza zbiór indeksów maszyn wyroczni, które zatrzymują się (po podaniu ich indeksu jako danych wejściowych) podczas używania X jako wyroczni. Zestaw X "nazywa się skok Turinga z X . Skok Turinga o stopień [ X ] jest zdefiniowany jako stopień [ X ′]; jest to prawidłowa definicja, ponieważ X ′ ≡ _T Y ′ zawsze, gdy X ≡ _T Y . Kluczowym przykładem jest 0 , stopień problemu zatrzymania .

Podstawowe własności stopni Turinga

• Każdy stopień Turinga jest przeliczalnie nieskończony , to znaczy zawiera dokładnie zbiory.${\displaystyle \aleph_{0}}$
• Istnieją wyraźne stopnie Turinga.${\ Displaystyle 2 ^ {\ aleph _ {0}}}$
• Dla każdego stopnia a zachodzi ścisła nierówność a < a ′.
• Dla każdego stopnia a zestaw stopni poniżej a jest policzalny . Zbiór stopni większych niż a ma size .${\ Displaystyle 2 ^ {\ aleph _ {0}}}$

Struktura stopni Turinga

Przeprowadzono wiele badań nad strukturą stopni Turinga. W poniższej ankiecie wymieniono tylko niektóre z wielu znanych wyników. Z badań można wyciągnąć jeden ogólny wniosek, że struktura stopni Turinga jest niezwykle skomplikowana.

Zamów właściwości

• Są minimalne stopnie . Stopień a jest minimalny, jeśli a jest niezerowe i nie ma stopnia między 0 a a . Zatem relacja porządku na stopniach nie jest porządkiem gęstym .
• Dla każdego niezerowego stopnia a istnieje stopień b nieporównywalny z a .
• Istnieje zestaw parami nieporównywalnych stopni Turinga.${\ Displaystyle 2 ^ {\ aleph _ {0}}}$
• Istnieją pary stopni bez największej dolnej granicy. Tak więc nie jest kratą.${\displaystyle {\mathcal {D}}}$
• Każdy policzalny częściowo zamówiony zestaw może być osadzony w stopniach Turinga.
• Żaden nieskończony, ściśle rosnący ciąg stopni nie ma górnego ograniczenia.

Właściwości dotyczące skoku

• Dla każdego stopnia a istnieje stopień ściśle pomiędzy a i a′ . W rzeczywistości istnieje policzalna rodzina parami nieporównywalnych stopni między a i a′ .
• Inwersja skoku: stopień a ma postać b′ wtedy i tylko wtedy, gdy 0′ ≤ a .
• Dla dowolnego stopnia a istnieje stopień b taki, że a < b i b′ = a′ ; taki stopień b nazywamy niskim w stosunku do a .
• Istnieje nieskończona sekwencja a _i stopni taka, że a ′ _{i +1} ≤ a _i dla każdego i .

Właściwości logiczne

• Simpson (1977) wykazały, że w pierwszej kolejności teoria stanowi w języku ⟨≤, =⟩ lub ⟨≤ ", =⟩ jest wielu jeden odpowiednik teorii prawdziwej arytmetyki drugiego rzędu . Wskazuje to, że struktura jest niezwykle skomplikowana.${\displaystyle {\mathcal {D}}}$${\displaystyle {\mathcal {D}}}$
• Shore i Slaman (1999) pokazali, że operator skoku jest definiowalny w strukturze pierwszego rzędu z językiem ⟨ ≤, = ⟩ .${\displaystyle {\mathcal {D}}}$

Rekurencyjnie przeliczalne stopnie Turinga

Skończona siatka, której nie można osadzić w stopniach.

Stopień jest nazywany rekurencyjnie przeliczalnym (re), jeśli zawiera zbiór rekurencyjnie przeliczalny . Każdy stopień re jest poniżej 0′ , ale nie każdy stopień poniżej 0′ jest re.

• ( GE Sacks , 1964) Stopnie są gęste; pomiędzy dowolnymi dwoma stopniami re istnieje trzeci stopień re.
• (AH Lachlan, 1966a i CEM Yates, 1966) Istnieją dwa stopnie re bez największego ograniczenia dolnego dla stopni re.
• (AH Lachlan, 1966a i CEM Yates, 1966) Istnieje para niezerowych re stopni, których największym dolnym ograniczeniem jest 0 .
• (AH Lachlan, 1966b) Nie ma pary stopni re, której największe ograniczenie dolne to 0, a najmniejsze ograniczenie górne to 0′ . Ten wynik jest nieformalnie nazywany twierdzeniem niediamentowym .
• (SK Thomason, 1971) Każda skończona sieć rozdzielcza może być osadzona w restopniach. W rzeczywistości policzalna bezatomowa algebra Boole'a może być osadzona w sposób, który zachowuje suprema i infima .
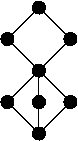
• (AH Lachlan i RI Soare , 1980) Nie wszystkie skończone sieci mogą być osadzone w re stopniach (poprzez osadzenie, które zachowuje supremę i infima). Po prawej stronie pokazano konkretny przykład.
• ( LA Harrington i TA Slaman , patrz Nies, Shore i Slaman (1998)) Teoria pierwszego rzędu stopni re w języku ⟨ 0 , ≤, = ⟩ jest równoważna teorii prawdziwego pierwszego rzędu arytmetyka .

Problem posta i metoda pierwszeństwa

Emil Post zbadał stopnie re Turinga i zapytał, czy istnieje jakikolwiek stopień re-turinga ściśle pomiędzy 0 a 0′ . Problem skonstruowania takiego stopnia (lub wykazania, że ​​żaden nie istnieje) stał się znany jako problem Posta . Problem ten został rozwiązany niezależnie przez Friedberga i Muchnika w latach 50. XX wieku, którzy wykazali, że te pośrednie stopnie naukowe istnieją. Każdy z ich dowodów rozwinął tę samą nową metodę konstruowania re stopni, która stała się znana jako metoda priorytetowa . Metoda priorytetów jest obecnie główną techniką ustalania wyników dotyczących resetowania.

Ideą metody priorytetowej konstruowania resetu X jest wypisanie policzalnej sekwencji wymagań, które X musi spełnić. Na przykład, aby skonstruować zbiór X pomiędzy 0 a 0′ wystarczy spełnić wymagania A _e i B _e dla każdej liczby naturalnej e , gdzie A _e wymaga, aby wyrocznia o indeksie e nie obliczała 0′ z X a B _e wymaga, aby maszyna Turinga z indeksem e (i bez wyroczni) nie obliczała X . Wymagania te są umieszczane w kolejności priorytetowej , która jest wyraźną bijecją wymagań i liczb naturalnych. Dowód przebiega indukcyjnie z jednym stopniem dla każdej liczby naturalnej; etapy te można traktować jako etapy czasu, w których zbiór X jest wyliczany. Na każdym etapie liczby można wstawić do X lub na zawsze uniemożliwić wpisanie X w celu spełnienia wymagań (czyli zmusić je do zatrzymania, gdy wszystkie X zostaną wyliczone). Czasami liczba może być wyliczona do X w celu spełnienia jednego wymagania, ale wykonanie tego spowoduje, że wcześniej spełniony warunek stanie się niespełniony (to znaczy zostanie uszkodzony ). Kolejność priorytetów wymagań służy do określenia, które wymaganie należy spełnić w tym przypadku. Nieformalny pomysł polega na tym, że jeśli wymóg zostanie uszkodzony, to ostatecznie przestanie być uszkodzony po tym, jak wszystkie wymagania o wyższym priorytecie przestaną być uszkodzone, chociaż nie każdy argument priorytetowy ma tę właściwość. Należy argumentować, że cały zbiór X jest ponownie i spełnia wszystkie wymagania. Argumenty priorytetowe mogą służyć do udowodnienia wielu faktów dotyczących resetowania; zastosowane wymagania i sposób ich spełnienia muszą być starannie dobrane, aby uzyskać wymagany rezultat.

Zobacz też

• Martin środek

Bibliografia

Monografie (studia licencjackie)

• Cooper, Teoria obliczalności SB . Chapman & Hall / CRC, Boca Raton, FL, 2004. ISBN  1-58488-237-9
• Cutland, N. Obliczalność . Cambridge University Press, Cambridge-Nowy Jork, 1980. ISBN  0-521-22384-9 ; ISBN  0-521-29465-7

Monografie i artykuły ankietowe (poziom magisterski)

• Ambos-Spies, K. i Fejer, P. Stopnie nierozwiązywalności. Nieopublikowane. http://www.cs.umb.edu/~fejer/articles/History_of_Degrees.pdf
• Lerman, M. Stopnie nierozwiązywalności. Perspektywy w logice matematycznej. Springer-Verlag, Berlin, 1983. ISBN  3-540-12155-2
• Odifreddi, PG (1989), Klasyczna teoria rekurencji , Studia w logice i podstawach matematyki, 125 , Amsterdam: North-Holland, ISBN 978-0-444-87295-1, MR  0982269
• Odifreddi, PG (1999), Klasyczna teoria rekurencji. Tom. II , Studies in Logic and the Foundations of Mathematics, 143 , Amsterdam: North-Holland, ISBN 978-0-444-50205-6, MR  1718169
• Rogers, H. Teoria funkcji rekurencyjnych i efektywnej obliczalności , MIT Press. ISBN  0-262-68052-1 , ISBN  0-07-053522-1
• Sacks, Gerald E. Degrees of Unsolvability (Annals of Mathematics Studies), Princeton University Press. ISBN  978-0-6910-7941-7
• Simpson, S. Stopnie nierozwiązywalności: przegląd wyników. Handbook of Mathematical Logic , North-Holland, 1977, s. 631-652.
• Shoenfield, Joseph R. Stopnie nierozwiązywalności , North-Holland/Elsevier, ISBN  978-0-7204-2061-6 .
• Shore, R. (1993). „Teorie T, tt i wtt re stopni: nierozstrzygalność i poza”. Na Uniw. Nac. del Sur, Bahía Blanca (red.). Materiały z IX Sympozjum Ameryki Łacińskiej na temat logiki matematycznej, część 1 (Bahía Blanca, 1992) . Notatki Lógica Mat. 38 . s. 61-70.
• Soare, R. Zbiory i stopnie rekurencyjnie przeliczalne. Perspektywy w logice matematycznej. Springer-Verlag, Berlin, 1987. ISBN  3-540-15299-7
• Soare, Robert I. Zbiory i stopnie rekurencyjnie przeliczalne. Byk. Amer. Matematyka. Soc. 84 (1978), nr. 6, 1149-1181. MR 508451

Artykuły naukowe

• Kleene'a, Stephena Cole'a ; Post, Emil L. (1954), „Górna pół-krata stopni rekurencyjnej nierozwiązywalności”, Annals of Mathematics , Druga seria, 59 (3): 379-407, doi : 10.2307/1969708 , ISSN  0003-486X , JSTOR  1969708 , MR  0061078
• Lachlan, AH (1966a), „Dolne granice dla par rekurencyjnie przeliczalnych stopni”, Proceedings of the London Mathematical Society , 3 (1): 537-569, CiteSeerX  10.1.1.106.7893 , doi : 10.1112/plms/s3-16,1 .537 .
• Lachlan, AH (1966b), „Niemożność znalezienia względnych dopełnień dla stopni rekurencyjnie przeliczalnych”, J. Symb. Dziennik. , 31 (3): 434–454, doi : 10.2307/2270459 , JSTOR  2270459 .
• Lachlan, AH; Soare, RI (1980), „Nie każda skończona krata jest osadzona w rekurencyjnie przeliczalnych stopniach”, Advances in Mathematics , 37 : 78-82, doi : 10.1016/0001-8708 (80) 90027-4 .
• Nies, Andrzej; Shore, Richard A.; Slaman, Theodore A. (1998), „Interpretowalność i definiowalność w stopniach rekurencyjnie przeliczalnych”, Proceedings of the London Mathematical Society , 77 (2): 241–291, CiteSeerX  10.1.1.29.9588 , doi : 10.1112/S002461159800046X , ISSN  0024-6115 , MR  1635141
• Post, Emil L. (1944), „Rekurencyjnie przeliczalne zestawy liczb całkowitych dodatnich i ich problemy decyzyjne”, Biuletyn Amerykańskiego Towarzystwa Matematycznego , 50 (5): 284-316, doi : 10.1090/S0002-9904-1944-08111- 1 , ISSN  0002-9904 , MR  0010514
• Sacks, GE (1964), „stopnie rekurencyjnie przeliczalne są gęste”, Annals of Mathematics , Druga seria, 80 (2): 300-312, doi : 10.2307/1970393 , JSTOR  1970393 .
• Shore, Richard A. ; Slaman, Theodore A. (1999), "Definiowanie skoku Turinga", Mathematical Research Letters , 6 (6): 711-722, doi : 10.4310/mrl.1999.v6.n6.a10 , ISSN  1073-2780 , MR  1739227
• Simpson, Stephen G. (1977), „Teoria pierwszego rzędu stopni nierozwiązywalności rekurencyjnej”, Annals of Mathematics , Druga seria, 105 (1): 121-139, doi : 10.2307/1971028 , ISSN  0003-486X , JSTOR  1971028 , MR  0432435
• Thomason, SK (1971), „Podsieci stopni rekurencyjnie przeliczalnych”, Z. Math. Logik Grundlag. Matematyka. , 17 : 273–280, doi : 10.1002/malq.19710170131 .
• Yates, CEM (1966), „Minimalna para stopni rekurencyjnie przeliczalnych”, Journal of Symbolic Logic , 31 (2): 159-168, doi : 10.2307/2269807 , JSTOR  2269807 .