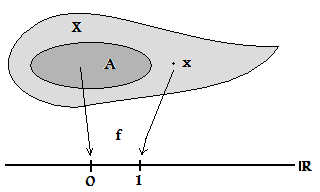
Przestrzeń Tychonowa - Tychonoff space
|
Aksjomaty separacji w przestrzeniach topologicznych | |
|---|---|
| Klasyfikacja Kołmogorowa | |
| T 0 | (Kołmogorów) |
| T 1 | (Fréchet) |
| T 2 | (Hausdorffa) |
| T 2 ½ | (Urysohna) |
| całkowicie T 2 | (całkowicie Hausdorff) |
| T 3 | (zwykły Hausdorff) |
| T 3½ | (Tychonoff) |
| T 4 | (normalny Hausdorff) |
| T 5 | (całkowicie normalny Hausdorff) |
| T 6 | (zupełnie normalny Hausdorff) |
W topologii i pokrewnych dziedzin matematyki , przestrzenie Tichonowa i całkowicie regularne przestrzenie są rodzaje przestrzeni topologicznych . Warunki te są przykładami aksjomatów separacji .
Przestrzenie Tychonowa noszą imię Andrieja Nikołajewicza Tychonowa , którego rosyjskie imię (Тихонов) jest różnie oddawane jako „Tychonow”, „Tichonow”, „Tichonow”, „Tichonow” itp., który wprowadził je w 1930 roku, aby uniknąć patologicznej sytuacji Hausdorffa przestrzenie, których jedynymi ciągłymi funkcjami o wartościach rzeczywistych są stałe odwzorowania.
Definicje
Przestrzeń topologiczną nazywa się całkowicie regularną, jeśli punkty można oddzielić od zbiorów zamkniętych za pomocą (ograniczonych) ciągłych funkcji o wartościach rzeczywistych. Z technicznego punktu widzenia oznacza to: dla każdego zbioru domkniętego i dowolnym momencie istnieje na wartościach rzeczywistych funkcji ciągłych takie, że a (Równoważnie można wybrać dowolne dwie wartości zamiast a , a nawet domagać się być ograniczonym funkcja).
Przestrzeń topologiczna jest nazywany przestrzenią Tichonowa (alternatywnie: ţ 3² przestrzeń lub ţ gatunku przestrzeń lub całkowicie T 3 miejsca ), jeżeli jest to całkowicie regularny odstęp Hausdorff .
Uwaga. Przestrzenie całkowicie regularne i przestrzenie Tychonowa są powiązane pojęciem równoważności Kołmogorowa . Przestrzeń topologiczna to Tychonow wtedy i tylko wtedy, gdy jest zarówno całkowicie regularna, jak i T 0 . Z drugiej strony, przestrzeń jest całkowicie regularna wtedy i tylko wtedy, gdy jej iloraz Kołmogorowa wynosi Tychonow.
Konwencje nazewnictwa
W literaturze matematycznej stosuje się różne konwencje, jeśli chodzi o termin „całkowicie regularny” i „T”-aksjomaty. Definicje w tej sekcji są w typowym współczesnym użyciu. Niektórzy autorzy zamieniają jednak znaczenia tych dwóch rodzajów terminów lub używają wszystkich terminów zamiennie. W Wikipedii terminy „całkowicie regularne” i „Tychonoff” są używane swobodnie i generalnie unika się notacji „T”. W standardowej literaturze zaleca się zatem ostrożność, aby dowiedzieć się, jakich definicji używa autor. Aby uzyskać więcej informacji na ten temat, zobacz Historia aksjomatów separacji .
Przykłady i kontrprzykłady
Niemal każda przestrzeń topologiczna badana w analizie matematycznej jest Tychonowa, a przynajmniej całkowicie regularna. Na przykład, rzeczywista linia to Tychonoff w standardowej topologii euklidesowej . Inne przykłady obejmują:
- Każda przestrzeń metryczna to Tychonow; każda przestrzeń pseudometryczna jest całkowicie regularna.
- Każda lokalnie zwarta regularna przestrzeń jest całkowicie regularna, a zatem każda lokalnie zwarta przestrzeń Hausdorffa to Tychonow.
- W szczególności każda rozmaitość topologiczna to Tychonow.
- Każdy kompletnie uporządkowany zestaw z topologią kolejności to Tychonow.
- Każda grupa topologiczna jest całkowicie regularna.
- Uogólniając zarówno przestrzenie metryczne, jak i grupy topologiczne, każda jednolita przestrzeń jest całkowicie regularna. Prawdą jest również odwrotność: każda całkowicie regularna przestrzeń jest uniformizowalna.
- Każdy kompleks CW to Tychonow.
- Każda normalna regularna przestrzeń jest całkowicie regularna, a każda normalna przestrzeń Hausdorffa to Tychonow.
- Niemyckiego samolot jest przykładem przestrzeni Tichonowa, która nie jest normalne .
Nieruchomości
Ochrona
Całkowita regularność i własność Tychonowa są dobrze zachowane w odniesieniu do początkowych topologii . W szczególności, pełna regularność jest zachowywana przez zastosowanie dowolnych topologii początkowych, a właściwość Tychonowa jest zachowywana przez wybieranie topologii początkowych rozdzielających punkty. Wynika, że:
- Każda podprzestrzeń przestrzeni całkowicie regularnej lub przestrzeni Tychonowa ma tę samą własność.
- Niepuste pole produktu jest całkowicie regularne (odpowiednio Tychonoff) wtedy i tylko wtedy, gdy każde pole czynników jest całkowicie regularne (odpowiednio Tychonoff).
Jak wszystkie aksjomaty separacji, przy ostatecznych topologiach nie zachowuje się pełnej regularności . W szczególności iloraz przestrzeni całkowicie regularnych nie musi być regularny . Iloraz przestrzeni Tychonowa nie musi być nawet Hausdorffem . Istnieją zamknięte ilorazy płaszczyzny Moore'a, które dostarczają kontrprzykładów.
Funkcje ciągłe o wartościach rzeczywistych
Dla dowolnej przestrzeni topologicznej X , niech C ( X ) oznacza rodzinę funkcji ciągłych o wartościach rzeczywistych na X i niech C b ( X ) będzie podzbiorem ograniczonych funkcji ciągłych o wartościach rzeczywistych.
Przestrzenie całkowicie regularne charakteryzują się tym, że ich topologia jest całkowicie określona przez C ( X ) lub C b ( X ). W szczególności:
- Przestrzeń X jest całkowicie regularna wtedy i tylko wtedy, gdy ma początkową topologię indukowaną przez C ( X ) lub C b ( X ).
- Przestrzeń X jest całkowicie regularna wtedy i tylko wtedy, gdy każdy domknięty zbiór można zapisać jako przecięcie rodziny zbiorów zerowych w X (tzn. zbiory zer stanowią podstawę zbiorów domkniętych X ).
- Przestrzeń X jest całkowicie regularna wtedy i tylko wtedy, gdy zestawy cozero z X tworząc podstawę dla topologii X .
Biorąc pod uwagę dowolną przestrzeń topologiczną ( X , τ ) istnieje uniwersalny sposób skojarzenia całkowicie regularnej przestrzeni z ( X , τ ). Niech ρ będzie początkową topologią na X indukowaną przez C τ ( X ) lub, równoważnie, topologią generowaną przez bazę zbiorów cozero w ( X , τ). Wtedy ρ będzie najlepszą całkowicie regularną topologią na X, która jest grubsza niż τ. Ta konstrukcja jest uniwersalna w tym sensie, że każda ciągła funkcja
do całkowicie regularnej przestrzeni Y będzie ciągła na ( X , ρ). W języku teorii kategorii , funktor wysyłający ( X , τ) do ( X , ρ) pozostaje obok funktora inkluzji CReg → Top . Zatem kategoria całkowicie regularnych przestrzeniach creg jest refleksyjny podkategorii z góry , w kategorii przestrzeni topologicznych . Biorąc iloraz Kołmogorowa widać, że podkategoria przestrzeni Tychonowa jest również refleksyjna.
Można pokazać , że C τ ( X ) = C ρ ( X ) w powyższej konstrukcji tak , że pierścienie C ( X ) i C b ( X ) są zwykle badane tylko dla całkowicie regularnych przestrzeni X .
Kategoria rzeczywistych zwartych przestrzeni Tychonowa jest antyrównoważna kategorii pierścieni C ( X ) (gdzie X oznacza rzeczywiste zwarte przestrzenie) wraz z homomorfizmami pierścieni jako odwzorowaniami. Na przykład można zrekonstruować X z C ( X ), gdy X jest (rzeczywiste) zwarte. Teoria algebraiczna tych pierścieni jest zatem przedmiotem intensywnych badań. Rozległym uogólnieniem tej klasy pierścieni, która wciąż przypomina wiele własności przestrzeni Tychonowa, ale ma również zastosowanie w rzeczywistej geometrii algebraicznej , jest klasa rzeczywistych pierścieni zamkniętych .
Osadzania
Przestrzenie Tychonowa to dokładnie te przestrzenie, które można osadzić w zwartych przestrzeniach Hausdorffa . Dokładniej, dla każdej przestrzeni Tychonowa X istnieje zwarta przestrzeń Hausdorffa K taka, że X jest homeomorficzna z podprzestrzenią K .
W rzeczywistości zawsze można wybrać K jako sześcian Tychonowa (tzn. być może nieskończony iloczyn przedziałów jednostkowych ). Każda kostka Tychonowa jest zwartą Hausdorffem w wyniku twierdzenia Tychonowa . Ponieważ każda podprzestrzeń zwartej przestrzeni Hausdorffa to Tychonow, mamy:
- Przestrzeń topologiczna jest Tychonowa wtedy i tylko wtedy, gdy może być osadzona w kostce Tychonowa .
Zagęszczenia
Szczególnie interesujące są te zanurzenia, w których obraz X jest gęsty w K ; nazywane są one Hausdorffa zwartych z X . Biorąc pod uwagę każdą osadzanie przestrzeni Tichonowa X w zwartej przestrzeni Hausdorffa K zamknięcie wizerunku X w K jest zwartym X . W tym samym artykule z 1930 roku, w którym Tychonoff zdefiniował całkowicie regularne przestrzenie, udowodnił również, że każda przestrzeń Tychonoffa ma zagęszczenie Hausdorffa.
Wśród tych zagęszczeń Hausdorffa istnieje unikalne, „najbardziej ogólne” zagęszczenie Stone-Čech β X . Charakteryzuje się ona tym właściwości uniwersalnego , który, biorąc pod uwagę ciągłą mapę F od X do innych zwartej Hausdorffa Y , jest unikalny stały mapę g z p X do Y , która rozciąga f w tym sensie, że F jest kompozycja o g i j .
Jednolite struktury
Pełna regularność jest właśnie warunkiem koniecznym istnienia jednorodnych struktur w przestrzeni topologicznej. Innymi słowy, każda jednolita przestrzeń ma całkowicie regularną topologię i każda całkowicie regularna przestrzeń X jest uniformizowalna . Przestrzeń topologiczna dopuszcza wyodrębnioną jednolitą strukturę wtedy i tylko wtedy, gdy jest nią Tychonow.
Biorąc pod uwagę całkowicie regularna przestrzeń X jest zazwyczaj więcej niż jeden jednolitość na X , który jest kompatybilny z topologią X . Jednak zawsze będzie istniała najlepsza kompatybilna jednorodność, zwana dokładną jednolitością na X . Jeśli X jest Tychonow, to struktura jednorodna może być wybrana tak, że β X staje się uzupełnieniem przestrzeni jednorodnej X .
Cytaty
Bibliografia
- Gillman, Leonard ; Jerison, Meyer (1960). Pierścienie funkcji ciągłych . Graduate Texts in Mathematics, nr 43 (Dover przedruk red.). NY: Springer Verlag. str. xiii. Numer ISBN 978-048681688-3.
- Narici, Lawrence ; Beckenstein, Edward (2011). Topologiczne przestrzenie wektorowe . Matematyka czysta i stosowana (wyd. drugie). Boca Raton, FL: CRC Press. Numer ISBN 978-1584888666. OCLC 144216834 .
- Willard, Stephen (1970). Ogólna topologia (Dover przedruk red.). Reading, Massachusetts: Addison-Wesley Publishing Company. Numer ISBN 0-486-43479-6.