Transformacja Galileusza - Galilean transformation

W fizyki , A Galilejczyku transformacja jest wykorzystywana do przekształcania współrzędnych między dwoma ramkami odniesienia , które różnią się tylko przy ciągłym ruchu względnego w konstruktach fizyki Newtona . Te przekształcenia wraz z rotacjami przestrzennymi i przesunięciami w przestrzeni i czasie tworzą niejednorodną grupę galileuszową (przyjętą poniżej). Bez tłumaczeń w przestrzeni i czasie grupa jest jednorodną grupą galilejską . Grupa Galilejczyku jest grupa wniosków o galilejskim wzgl działających na czterech wymiarów przestrzeni i czasie formowania Galilejczyk geometrii . To jest punkt widzenia pasywnej transformacji . W szczególnej teorii względności jednorodne i niejednorodne transformacje Galileusza są odpowiednio zastępowane transformacjami Lorentza i transformacjami Poincarégo ; odwrotnie, skrócenie grupy w klasycznej granicy c → ∞ transformacji Poincarégo daje transformacje Galileusza.

Poniższe równania są poprawne fizycznie tylko w systemie newtonowskim i nie mają zastosowania do układów współrzędnych poruszających się względem siebie z prędkościami zbliżonymi do prędkości światła .

Galileusz sformułował te koncepcje w swoim opisie ruchu jednostajnego . Temat był motywowany przez jego opisie ruchu na kulki staczania się rampy , w którym zmierzył wartość liczbową dla przyspieszenia od ciężkości blisko powierzchni Ziemi .

Tłumaczenie

Standardowa konfiguracja układów współrzędnych dla transformacji Galileusza.

Mimo, że transformacje są nazwane Galileo, to czas bezwzględny i przestrzeń jako stworzone przez Isaaca Newtona , który zapewnia ich domenę definicji. W istocie transformacje Galileusza ucieleśniają intuicyjne pojęcie dodawania i odejmowania prędkości jako wektorów .

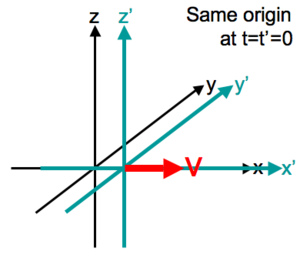
Poniższy zapis opisuje zależność w transformacji Galileusza pomiędzy współrzędnymi ( x , y , z , t ) i ( x ′, y ′, z ′, t ′) pojedynczego zdarzenia arbitralnego, mierzonego w dwóch układach współrzędnych S i S′ , w jednostajnym ruchu względnym ( prędkość v ) we wspólnych kierunkach x i x ′ , przy czym ich początki przestrzenne pokrywają się w czasie t = t ′ = 0 :

${\displaystyle x'=x-vt}$

${\displaystyle y'=y}$

${\displaystyle z'=z}$

${\displaystyle t'=t.}$

Zauważ, że ostatnie równanie obowiązuje dla wszystkich transformacji Galileusza aż do dodania stałej i wyraża założenie o uniwersalnym czasie niezależnym od względnego ruchu różnych obserwatorów.

W języku algebry liniowej transformacja ta jest uważana za odwzorowanie ścinania i jest opisana macierzą działającą na wektorze. Przy ruchu równoległym do osi x transformacja działa tylko na dwie składowe:

${\ Displaystyle {\ zacznij {pmatrix} x '\\ t' \ koniec {pmatrix}} = {\ zacznij {pmatrix} 1 i V \ \ 0 i 1 \ koniec {pmatrix}} {\ zacznij {pmatrix} x \ \ t \end{pmacierz}}}$

Chociaż reprezentacje macierzowe nie są bezwzględnie konieczne do transformacji Galileusza, dostarczają środków do bezpośredniego porównania z metodami transformacji w szczególnej teorii względności.

Transformacje Galileusza

Galilejczyk symetrie może być zapisana jako kompozycji z obrotu , w tłumaczeniu i ruchem jednostajnym czasoprzestrzeni. Niech x reprezentuje punkt w przestrzeni trójwymiarowej, a t punkt w czasie jednowymiarowym. Ogólny punkt w czasoprzestrzeni jest określony przez uporządkowaną parę ( x , t ) .

Ruch jednostajny o prędkości v , jest określony wzorem

${\ Displaystyle (\ mathbf {x} , t) \ mapsto (\ mathbf {x} + t \ mathbf {v}, t)}$

gdzie v ∈ R ³ . Tłumaczenie podaje

${\ Displaystyle (\ mathbf {x} t) \ mapsto (\ mathbf {x} + \ mathbf {a} t + s)}$

gdzie ∈ R ³ i y ∈ R . Rotacja jest podana przez

${\ Displaystyle (\ mathbf {x} , t) \ mapsto (G \ mathbf {x} , t)}$

gdzie G  : R ³ → R ³ jest transformacją ortogonalną .

Jako grupa Liego grupa przekształceń Galileusza ma wymiar 10.

grupa galilejska

Dwa Galilejskich Transformations G ( R , V , , s ) i G ( R” , v ', ', y ') komponować z wytworzeniem trzeciego transformacji Galilejczykiem

G ( R ′, v ′, a ′, s ′) ⋅ G ( R , v , a , s ) = G ( R ′ R , R ′ v + v ′ , R ′ a + a ′ + v ′ s , s ′ + s ) .

Zbiór wszystkich przekształceń Galileusza Gal(3) tworzy grupę, której działaniem grupowym jest kompozycja.

Grupa jest czasami reprezentowana jako grupa macierzowa ze zdarzeniami czasoprzestrzennymi ( x , t , 1) jako wektorami, gdzie t jest rzeczywiste, a x ∈ R ³ jest pozycją w przestrzeni. Działanie jest podana przez

${\ Displaystyle {\ zacznij {pmatrix} R & v & a \ \ 0 i 1 & s \ \ 0 i 0 i 1 \ koniec {pmatrix}} {\ zacznij {pmatrix} x \ \ t \ \ 1 \ koniec {pmatrix}} = {\ rozpocznij {pmatrix} Rx + vt+a\\t+s\\1\end{pmatrix}},}$

gdzie a jest rzeczywisty i v , x , ∈ R ³ i R jest macierz obrotu . Kompozycję przekształceń uzyskuje się następnie poprzez mnożenie macierzy . W dyskusji należy uważać, czy ograniczamy się do połączonej grupy składowej przekształceń ortogonalnych.

Gal(3) nazwał podgrupy. Komponent tożsamości jest oznaczony jako SGal(3) .

Niech m reprezentuje macierz transformacji z parametrami v , R , s , a :

• ${\displaystyle \{m:R=I_{3}\},}$ przemiany anizotropowe.
• ${\ Displaystyle \ {m: s = 0 \}}$ przemiany izochroniczne.
• ${\ Displaystyle \ {m: s = 0, v = 0 \},}$ przestrzenne przekształcenia euklidesowe.
• ${\displaystyle G_{1}=\{m:s=0,a=0\}}$ przekształcenia jednostajnie specjalne / przekształcenia jednorodne, izomorficzne do przekształceń euklidesowych.
• ${\ Displaystyle G_ {2} = \ {m: v = 0, R = I_ {3}\} \ cong (\ mathbf {R} ^ {4}+),}$ przesunięcia pochodzenia / translacji w czasoprzestrzeni Newtona.
• ${\ Displaystyle G_ {3} = \ {m: s = 0, a = 0, v = 0 \} \ cong \ operatorname {SO} (3),}$obroty (ramki odniesienia) (patrz SO(3) ), zwarta grupa.
• ${\ Displaystyle G_ {4} = \ {m: s = 0, a = 0, R = I_ {3} \} \ cong (\ mathbf {R} ^ {3}, +),}$ jednolite ruchy/wzmocnienia ramy.

Parametry a , V , R , okres dziesięciu wymiarach. Ponieważ transformacje zależą w sposób ciągły od s , v , R , a , Gal(3) jest grupą ciągłą , zwaną także grupą topologiczną.

Strukturę Gal(3) można zrozumieć poprzez rekonstrukcję z podgrup. Produkt iloczynów kombinacji ( są) z grupy. ${\displaystyle A\rrazy B}$

1. ${\ Displaystyle G_ {2} \ triangleleft \ operatorname {SGal} (3)}$( G ₂ to normalna podgrupa )
2. ${\ Displaystyle \ operatorname {SGal} (3) \ cong G_ {2} \ rrazy G_ {1}}$
3. ${\ Displaystyle G_ {4}\ trianglelefteq G_ {1}}$
4. ${\displaystyle G_{1}\cong G_{4}\rrazy G_{3}}$
5. ${\ Displaystyle \ operatorname {SGal} (3) \ cong \ mathbf {R} ^ {4} \ rrazy (\ mathbf {R} ^ {3} \ rrazy \ operatorname {SO} (3)).}$

Pochodzenie w skurczu grupy

Algebra Lie z galilejskim grupy są łączone przez H , P, _I , C _ı i L _ij (e antysymetryczna tensora ), z zastrzeżeniem stosunków komutacyjnych , gdzie

${\ Displaystyle [H, P_ {i}] = 0}$

${\ Displaystyle [P_ {i}, P_ {j}] = 0}$

${\ Displaystyle [L_ {ij}, H] = 0}$

${\ Displaystyle [C_ {i}, C_ {j}] = 0}$

${\ Displaystyle [L_ {ij}, L_ {kl}] = ja [\ delta _ {ik} L_ {jl} - \ delta _ {il} L_ {jk} - \ delta _ {jk} L_ {il} + \delta _{jl}L_{ik}]}$

${\ Displaystyle [L_ {ij}, P_ {k}] = ja [\ delta _ {ik} P_ {j} - \ delta _ {jk} P_ {i}]}$

${\ Displaystyle [L_ {ij}, C_ {k}] = ja [\ delta _ {ik} C_ {j} - \ delta _ {jk} C_ {i}]}$

${\ Displaystyle [C_ {i}, H] = IP_ {i} \ \!}$

${\ Displaystyle [C_ {i}, P_ {j}] = 0 ~.}$

H jest generatorem przesunięć czasowych ( hamiltonian ), P _i jest generatorem przesunięć ( operator pędu ), C _i jest generatorem bezobrotowych przekształceń Galileusza (wzmocnienia Galileusza), a L _ij jest generatorem obrotów ( operator momentu pędu ) ).

Ta Lie Algebra jest postrzegana jako specjalna granica klasyczna algebry grupy Poincarégo , w granicy c → ∞ . Technicznie rzecz biorąc, grupa Galileusza jest słynnym skróceniem grupy grupy Poincaré (która z kolei jest skróceniem grupy grupy de Sitter SO(1,4) ). Formalnie zmieniając nazwę generatorów pędu i doładowania tych ostatnich na in

P ₀ ↦ H / C

K _i ↦ C ⋅ C _i ,

gdzie c jest prędkością światła (lub dowolną jego nieograniczoną funkcją), relacje komutacji (stałe strukturalne) w granicy c → ∞ przyjmują relacje z tych pierwszych. Zidentyfikowano generatory przesunięć czasu i rotacji. Zwróć także uwagę na niezmienniki grupy L _mn L ^mn oraz P _i P ⁱ .

W postaci macierzowej, dla d = 3 , można rozważyć reprezentację regularną (wbudowaną w GL(5; R ) , z której można ją wyprowadzić przez skrócenie pojedynczej grupy, z pominięciem grupy Poincarégo),

${\ Displaystyle iH = \ lewo ({\ zacząć {tablica} 0 i 0 i 0 i 0 i 0 \\ 0 i 0 i 0 i 0 i 0 \\ 0 i 0 i 0 i 0 i 0 \\ 0 i 0 i 0 i 0 i 1 \\ 0 i 0 i 0 i 0 i 0 \\\ koniec {array}} \ po prawej), \ qquad}$ ${\ Displaystyle i {\ vec {a}} \ cdot {\ vec {P}} = \ lewo ({\ zacznij {tablica} {ccccc} 0 i 0 i 0 i 0 i 0 i a_ {1} \\ 0 i 0 i 0 i 0 i a_ {2}\\ 0 i 0 i 0 i 0 i a_ {3}\ \0&0&0&0&0\\0&0&0&0&0\\\end{array}}\right),\qquad }$ ${\ Displaystyle i {\ vec {v}} \ cdot {\ vec {C}} = \ lewo ({\ zacznij {tablica} {ccccc} 0 i 0 i 0 i v_ {1} i 0 \ \ 0 i 0 i 0 i v_ {2} i 0 \ \ 0 i 0 i 0 i v_ {3 }&0\\0&0&0&0&0\\0&0&0&0&0\\\end{array}}\right),\qquad }$ ${\ Displaystyle i \ theta _ {i} \ epsilon ^ {ijk} L_ {jk} = \ lewo ({\ zacząć tablicę} {ccccc} 0 & \ theta _ {3} i - \ theta _ {2} i 0 i 0 \ \-\theta _{3}&0&\theta _{1}&0&0\\\theta _{2}&-\theta _{1}&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0\\\end{array}}\right) ~.}$

Nieskończenie mały element grupy to

${\ Displaystyle G (R {\ vec {v}}, {\ vec {a}}, s) = 1 \! \! 1_ {5} + \ lewo ({\ rozpocząć {tablicę} {ccccc} 0 i \ theta _{3}&-\theta _{2}&v_{1}&a_{1}\\-\theta _{3}&0&\theta _{1}&v_{1}&a_{2}\\\theta _ {2}&-\theta _{1}&0&v_{1}&a_{3}\\0&0&0&0&s\\0&0&0&0&0&0\\\end{array}}\right)+\ ...~.}$

Centralne rozszerzenie grupy Galilejskiej

Można rozważyć centralne rozszerzenie algebry Liego grupy Galileusza, rozpięte przez H ′, P ′ _i , C ′ _i , L ′ _ij oraz operator M : Tak zwaną algebrę Bargmanna otrzymuje się przez nałożenie , takie, że M leży w centrum , czyli dojeżdża ze wszystkimi innymi operatorami. ${\ Displaystyle [C'_ {i}, P'_ {j}] = iM \ delta _ {ij}}$

W całości ta algebra jest podana jako

${\ Displaystyle [H ', P' _ {i}] = 0 \ \!}$

${\ Displaystyle [P'_ {i}, P'_ {j}] = 0 \ \!}$

${\ Displaystyle [L'_ {ij}, H'] = 0 \ \!}$

${\ Displaystyle [C'_ {i}, C'_ {j}] = 0 \ \!}$

${\ Displaystyle [L '_ {ij}, L' _ {kl}] = ja [\ delta _ {ik} L '_ {jl} - \ delta _ {il} L' _ {jk} - \ delta _ {jk}L'_{il}+\delta _{jl}L'_{ik}]\,\!}$

${\ Displaystyle [L '_ {ij}, P'_ {k}] = i [\ delta _ {ik} P '_ {j} - \ delta _ {jk} P '_ {i}] \, \ !}$

${\ Displaystyle [L '_ {ij}, C '_ {k}] = i [\ delta _ {ik} C '_ {j} - \ delta _ {jk} C '_ {i}] \, \ !}$

${\ Displaystyle [C '_ {i}, H'] = IP '_ {i} \ \!}$

i w końcu

${\ Displaystyle [C'_ {i}, P'_ {j}] = iM \ delta _ {ij} ~.}$

gdzie pojawia się nowy parametr . To rozszerzenie i reprezentacje projekcyjne, które to umożliwia, są określone przez jego kohomologię grupową . ${\ Displaystyle M}$

Zobacz też

• Niezmienniczość Galileusza
• Teoria reprezentacji grupy Galileusza
• Formuła tensora Galilei-kowariancji
• Grupa Poincaré
• Grupa Lorentza
• Współrzędne Lagrange'a i Eulera

Uwagi

Bibliografia

• Arnold, VI (1989). Matematyczne metody mechaniki klasycznej (2 wyd.). Springer-Verlag. P. 6 . Numer ISBN 0-387-96890-3.
• Bargmann, V. (1954). „O jednostkowych reprezentacjach Ray ciągłych grup”. Roczniki Matematyki . 2. 59 (1): 1-46. doi : 10.2307/1969831 .
• Kopernik Mikołaj ; Keplera, Johannesa ; Galileusza, Galileusza ; Newtona, Izaaka ; Einstein, Albert (2002). Hawking, Stephen (red.). Na barkach gigantów: wielkie dzieła fizyki i astronomii . Filadelfia, Londyn: Running Press . s.  515–520 . Numer ISBN 0-7624-1348-4.
• Galilei, Galileusz (1638I). Discorsi e Dimostrazioni Matematiche, intorno á due nuoue scienze (po włosku). Leiden: Elsevier . s. 191-196.
• Galileusz, Galileusz (1638E). Dyskursy i demonstracje matematyczne dotyczące dwóch nowych nauk [ Discorsi e Dimostrazioni Matematiche Intorno a Due Nuove Scienze ]. Przetłumaczone na angielski 1914 przez Henry Crew i Alfonso de Salvio.
• Gilmore, Robert (2006). Grupy Liego, Algebry Liego i niektóre z ich zastosowań . Dover Książki o matematyce. Publikacje Dover . Numer ISBN 0486445291.
• Hoffmann, Banesh (1983), Teoria względności i jej korzenie , Scientific American Books, ISBN 0-486-40676-8, rozdział 5, s. 83
• Lerner, Lawrence S. (1996), Fizyka dla naukowców i inżynierów , 2 , Jones and Bertlett Publishers, Inc, ISBN 0-7637-0460-1, Rozdział 38 § 38 ust. 2, s. 1046,1047
• Pleśń, Richard A. (2002), Podstawowa teoria względności , Springer-Verlag, ISBN 0-387-95210-1, Rozdział 2 §2.6, s. 42
• Nadżafikhah, Mehdi; Owszem, Ahmad-Reza (2009). „Galilejska geometria ruchów” (PDF) . Nauki stosowane . s. 91–105.
• Serway, Raymond A.; Jewett, John W. (2006), Principles of Physics: A Calculus Text (4th ed.), Brooks / Cole - Thomson Learning, ISBN 0-534-49143-X, Rozdział 9 §9.1, s. 261