Elipsoida Jacobiego - Jacobi ellipsoid

Artystyczne przedstawienie Haumei , planety karłowatej o trójosiowym kształcie elipsoidalnym.

Jacobim elipsoida jest A trójosiowy (tj różnoboczny) elipsoidalne pod równowadze hydrostatycznej który powstaje, gdy siebie przyciągane płynem ustrojowym jednolitych gęstości obraca się ze stałą prędkością kątową. Jego nazwa pochodzi od niemieckiego matematyka Carla Gustava Jacobiego Jacobiego .

Historia

Przed Jacobim sferoida Maclaurina , która została sformułowana w 1742 roku, była uważana za jedyny typ elipsoidy, który może być w równowadze. Lagrange w 1811 rozważał możliwość, że trójosiowa elipsoida może być w równowadze, ale doszedł do wniosku, że dwie osie równikowe elipsoidy muszą być równe, co prowadzi z powrotem do rozwiązania sferoidy Maclaurina . Ale Jacobi zdał sobie sprawę, że demonstracja Lagrange'a jest warunkiem wystarczalności, ale nie jest to konieczne. Zauważył:

„Można popełnić poważny błąd, jeśli założy się, że sferoidy obrotu są jedynymi dopuszczalnymi figurami równowagi nawet przy restrykcyjnym założeniu powierzchni drugiego stopnia” (...) „W rzeczywistości proste rozważanie pokazuje, że elipsoidy o trzech nierównych osiach bardzo dobrze mogą być figurami równowagi, i że można przyjąć elipsę o dowolnym kształcie dla przekroju równikowego i wyznaczyć trzecią oś (która jest również najmniejszą z trzech osi) oraz prędkość kątową obrotu tak, że elipsoida jest figura równowagi”.

formuła Jacobiego

Półgłówne osie równikowe ( a , b ) i biegunowe ( c ) elipsoidy Jacobiego i sferoidy Maclaurina, w funkcji znormalizowanego momentu pędu, z zastrzeżeniem abc  = 1 (tj. dla stałej objętości 4π/3).
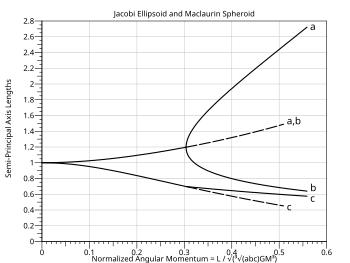
Linie przerywane odnoszą się do sferoidy Maclaurina w zakresie, w którym ma dynamiczną, ale nie świecką stabilność - rozluźni się w elipsoidę Jacobiego, pod warunkiem, że może rozproszyć energię dzięki lepkiemu płynowi składowemu.

W przypadku elipsoidy z równikowej pół-osi głównych i polarnego osi naczepy głównego , prędkość kątową o jest przez ${\displaystyle a\b}$${\displaystyle c}$${\ Displaystyle \ Omega}$${\displaystyle c}$

${\ Displaystyle {\ Frac {\ Omega ^ {2}} {\ pi G \ rho}} = 2abc \ int _ {0} ^ {\ infty} {\ Frac {u \ du} {(a ^ {2 }+u)(b^{2}+u)\Delta }}\ ,\quad \Delta ^{2}=(a^{2}+u)(b^{2}+u)(c^{ 2}+u),}$

gdzie jest gęstość i jest stałą grawitacyjną , z zastrzeżeniem warunku ${\ Displaystyle \ rho}$${\ Displaystyle G}$

${\ Displaystyle a ^ {2} b ^ {2} \ int _ {0} ^ { \ infty { \ frac {du} { (a ^ {2} + u) (b ^ {2} + u) \ Delta }}=c^{2}\int _{0}^{\infty }{\frac {du}{(c^{2}+u)\Delta }}.}$

Dla stałych wartości i , powyższy warunek ma rozwiązanie dla takich, że ${\displaystyle a}$${\displaystyle b}$${\displaystyle c}$

${\ Displaystyle {\ Frac {1} {c ^ {2}}}> {\ Frac {1} {a ^ {2}}} + {\ Frac {1} {b ^ {2}}}.}$

Całki można wyrazić jako niepełne całki eliptyczne . W odniesieniu do całki eliptycznej symetrycznej postaci Carlsona , wzór na prędkość kątową staje się ${\ Displaystyle R_ {J}}$

${\ Displaystyle {\ Frac {\ Omega ^ {2}} {\ pi G \ rho}} = {\ Frac {4abc} ​​{3 (a ^ {2}-b ^ {2})}} (a ^ { 2}R_{J}(a^{2},b^{2},c^{2},a^{2})-b^{2}R_{J}(a^{2},b^ {2},c^{2},b^{2}))}$

a warunkiem na względną wielkość półgłównych osi jest ${\displaystyle a,\ b,\ c}$

${\ Displaystyle {\ Frac {2} {3}}{\ Frac {a ^ {2} b {2} }{ b ^ {2}-a ^ {2}}} (R_ {J} (a ^ {2},b^{2},c^{2},a^{2})-R_{J}(a^{2},b^{2},c^{2},b^{2 }))={\frac {2}{3}}c^{2}R_{J}(a^{2},b^{2},c^{2},c^{2}).}$

Moment pędu elipsoidy Jacobiego jest podany przez ${\ Displaystyle L}$

${\ Displaystyle {\ Frac {L} {\ sqrt {GM ^ {3} {\ bar {a}}}}} = {\ Frac {\ sqrt {3}} {10}} {\ Frac {a ^ { 2}+b^{2}}{{\bar {a}}^{2}}}{\sqrt {\frac {\Omega ^{2}}{\pi G\rho }}}\ ,\quad {\bar {a}}=(abc)^{1/3},}$

gdzie jest masą elipsoidy i jest średnim promieniem , promieniem kuli o tej samej objętości co elipsoida. ${\ Displaystyle M}$${\displaystyle {\bar {a}}}$

Związek z elipsoidą Dedekinda

Elipsoidy Jacobiego i Dedekinda są obiema figurami równowagi dla ciała wirującego, jednorodnego, samograwitującego płynu. Jednakże, podczas gdy elipsoida Jacobiego obraca się w ciele, bez wewnętrznego przepływu płynu w obracającej się ramie, elipsoida Dedekind utrzymuje stałą orientację, z krążącym wewnątrz niej płynem składowym. Jest to bezpośrednia konsekwencja twierdzenia Dedekinda .

Dla dowolnego danego Jacobim elipsoidalne, istnieje Dedekind elipsoidy o tych samych pół-osi głównych i samej masie, w zakresie prędkości przepływu z ${\displaystyle a,\ b,\ c}$

${\ Displaystyle \ mathbf {u} = \ zeta {\ Frac {-a ^ {2} y \ mathbf {\ kapelusz {x}} + b ^ {2} x \ mathbf {\ kapelusz {y}}} {a ^{2}+b^{2}}},}$

gdzie są współrzędne kartezjańskie na osiach wyrównanych odpowiednio z osiami elipsoidy. Tutaj jest wirowość , który jest jednolity w całej sferoidy ( ). Prędkość kątowa elipsoidy Jacobiego i wirowość odpowiedniej elipsoidy Dedekinda są powiązane wzorem ${\ Displaystyle x \ y \ z}$${\displaystyle {\kapelusz {x}},\ {\kapelusz {y}},\ {\kapelusz {z}}}$${\displaystyle a,\ b,\ c}$${\ Displaystyle \ zeta}$${\ Displaystyle \ nabla \ razy \ mathbf {u} = \ zeta \ mathbf {\ kapelusz {z}}}$${\ Displaystyle \ Omega}$

${\ Displaystyle \ zeta = \ lewo ({\ Frac {a} {b}} + {\ Frac {b} {a}} \ prawej) \ Omega.}$

Oznacza to, że każda cząstka płynu elipsoidy Dedekind opisuje podobny obwód eliptyczny w tym samym okresie, w którym sferoida Jacobiego wykonuje jeden obrót.

W szczególnym przypadku elipsoidy Jacobiego i Dedekinda (oraz sferoida Maclaurina) stają się jednym i tym samym; rotacja ciała i przepływ kołowy sprowadzają się do tego samego. W tym przypadku , jak zawsze w przypadku sztywno obracającego się ciała. ${\displaystyle a=b}$${\ Displaystyle \ zeta = 2 \ Omega}$

W ogólnym przypadku elipsoidy Jacobiego i Dedekinda mają tę samą energię, ale moment pędu sferoidy Jacobiego jest większy o czynnik

${\ Displaystyle {\ Frac {L_ {\ operatorname {Jac}}} {L_ {\ operatorname {dat}}}} = {\ Frac {1} {2}} \ lewo ({\ Frac {a} {b} }+{\frac {b}{a}}\prawo).}$

Zobacz też

• Sferoid Maclaurina
• Elipsoida Riemanna
• Elipsoida Roche'a
• Elipsoidalny problem Dirichleta
• Sferoida
• Elipsoida

Bibliografia