Algorytm maksymalnego przepływu typu push-relabel - Push–relabel maximum flow algorithm

W optymalizacji matematycznej The algorytm push relabel (alternatywnie, algorytm wstępnego przepływu wypychania ) jest algorytm do obliczania maksymalnego przepływu w sieci przepływu . Nazwa „push – relabel” pochodzi od dwóch podstawowych operacji użytych w algorytmie. Przez cały czas wykonywania algorytm utrzymuje „przepływ wstępny” i stopniowo przekształca go w przepływ maksymalny, przemieszczając przepływ lokalnie między sąsiednimi węzłami za pomocą operacji wypychania pod kierownictwem dopuszczalnej sieci utrzymywanej przez operacje zmiany etykiety . Dla porównania, algorytm Forda-Fulkersona dokonuje globalnych ulepszeń, które wysyłają przepływ podążający ścieżkami od źródła aż do zlewu.

Algorytm push-relabel jest uważany za jeden z najbardziej wydajnych algorytmów maksymalnego przepływu. Algorytm ogólny ma silnie wielomianową złożoność czasową $O (V 2 E)$ , która jest asymptotycznie bardziej wydajna niż algorytm $O (VE 2)$ Edmondsa – Karpa . Poszczególne warianty algorytmów osiągają jeszcze mniejsze złożoności czasowe. Wariant oparty na zasadzie wyboru węzła o najwyższej etykiecie ma złożoność czasową $O (V 2 \sqrt E)$ i jest ogólnie uważany za punkt odniesienia dla algorytmów maksymalnego przepływu. Złożoność czasową Subcubic $O (VE log (V 2 / E))$ można osiągnąć za pomocą dynamicznych drzew , chociaż w praktyce jest to mniej wydajne.

Algorytm push-relabel został rozszerzony, aby obliczać minimalne przepływy kosztów . Pomysł etykiet odległości doprowadził do bardziej wydajnego algorytmu ścieżki rozszerzającej, który z kolei można włączyć z powrotem do algorytmu wypychania - relabelowania, aby stworzyć wariant o jeszcze wyższej wydajności empirycznej.

Historia

Koncepcja przepływu wstępnego została pierwotnie zaprojektowana przez Aleksandra V. Karzanowa i została opublikowana w 1974 r. W radzieckim wydaniu Mathematical Dokladi 15. Ten algorytm wstępnego przepływu również wykorzystywał operację wypychania; wykorzystał jednak odległości w sieci pomocniczej, aby określić, gdzie popchnąć przepływ, zamiast systemu etykietowania.

Algorytm push-relabel został zaprojektowany przez Andrew V. Goldberga i Roberta Tarjana . Algorytm został po raz pierwszy zaprezentowany w listopadzie 1986 w STOC '86: Proceedings z osiemnastego dorocznego sympozjum ACM nt. Teorii informatyki, a następnie oficjalnie w październiku 1988 roku jako artykuł w Journal of the ACM. Oba artykuły szczegółowo opisują ogólną formę algorytmu kończącego się w $O (V 2 E)$ wraz z implementacją sekwencyjną $O (V 3),$ implementacją $O (VE log (V 2 / E))$ przy użyciu drzew dynamicznych i implementacją równoległą / rozproszoną . Wyjaśniony w Goldberg-Tarjan wprowadził etykiety odległości poprzez włączenie ich do równoległego algorytmu maksymalnego przepływu Yossiego Shiloacha i Uzi Vishkina .

Koncepcje

Definicje i zapisy

Pozwolić:

$G = (V, E)$ być siecią o funkcji pojemności $c : V \times V \to ℝ \infty$ ,
$F = (G, C, y, t)$ sieć przepływu , gdzie $S \in V$ i $T \in V$ są wybrane źródłowych i opadanie wierzchołków, odpowiednio,
$f : V x V \to ℝ$ oznaczać wstępną przepływu w $F$ ,
$x f : V \to ℝ$ oznaczają funkcję nadmiaru względem przepływu $f$ , określoną przez $x f (u) = \sum v \in V f (v, u) - \sum v \in V f (u, v)$ ,
$c f : V \times V \to ℝ \infty$ oznaczają funkcję pojemności resztkowej w odniesieniu do przepływu $f$ , określoną przez $c f (e) = c (e) - f (e)$ ,
$E f \subset E$ to krawędzie, gdzie $f < c$ ,

i

$G F (V, E F)$ oznacza się resztkowe sieci z $G$ w stosunku do kierunku przepływu $f$ .

Algorytm push-relabel wykorzystuje nieujemną funkcję etykietowania, która jest prawidłową liczbą całkowitą, która wykorzystuje etykiety odległości lub wysokości na węzłach w celu określenia, które łuki powinny zostać wybrane do operacji wypychania. Ta funkcja oznaczania jest oznaczona przez $𝓁: V \to ℕ$ . Ta funkcja musi spełniać następujące warunki, aby została uznana za ważną:

Prawidłowe oznakowanie :

𝓁 (u) \leq 𝓁 (v) + 1

dla wszystkich

(u, v) \in E f

Stan źródła :

𝓁 (s) = | V |

Konserwacja zlewu :

𝓁 (t) = 0

W algorytmie wartości etykiet $s$ i $t$ są stałe. $𝓁 (u)$ jest dolną granicą nieważonej odległości od $u$ do $t$ w $G f,$ jeśli $t$ jest osiągalne z $u$ . Jeśli $u$ zostało odłączone od $t$ , to $𝓁 (u) - | V |$ jest dolną granicą nieważonej odległości od $u$ do $s$ . W rezultacie, jeśli istnieje prawidłowa funkcja etykietowania, nie ma ścieżek $s - t$ w $G f,$ ponieważ żadna z takich ścieżek nie może być dłuższa niż $| V | - 1$ .

Łuk $(u, v) \in E f$ nazywamy dopuszczalnym, jeśli $𝓁 (u) = 𝓁 (v) + 1$ . Dopuszczalne sieciowy $G F (V, é F)$ składa się z szeregu łuków $e \in e, f$ , które są dopuszczalne. Dopuszczalna sieć jest acykliczna.

Operacje

Inicjalizacja

Algorytm rozpoczyna się od utworzenia wykresu resztkowego, inicjalizacji wartości przepływu wstępnego do zera i wykonania zestawu operacji wypychania nasycenia na łukach resztkowych wychodzących ze źródła, $( s , v ), gdzie v ∈ V \ { s }$ . Podobnie, etykiety są inicjalizowane w taki sposób, że etykieta u źródła jest liczbą węzłów na wykresie, $𝓁 (s) = | V |$ , a wszystkim innym węzłom nadawana jest etykieta zero. Po zakończeniu inicjalizacji algorytm wielokrotnie wykonuje operacje wypychania lub zmiany etykiety na aktywnych węzłach, dopóki nie można wykonać żadnej odpowiedniej operacji.

Pchać

Operacja pchania dotyczy dopuszczalnego łuku zewnętrznego $(u, v)$ aktywnego węzła $u$ w $G f$ . Porusza $min {x f (u), c f (u, v)}$ jednostek przepływu z $u$ do $v$ .

push(u, v):
    assert x_f[u] > 0 and 𝓁[u] == 𝓁[v] + 1
    Δ = min(x_f[u], c[u][v] - f[u][v])
    f[u][v] += Δ
    f[v][u] -= Δ
    x_f[u] -= Δ
    x_f[v] += Δ

Operacja wypychania, która powoduje, że $f (u, v)$ osiąga $c (u, v),$ nazywana jest pchnięciem nasycającym, ponieważ wykorzystuje całą dostępną pojemność łuku resztkowego. W przeciwnym razie cały nadmiar w węźle jest przepychany przez pozostały łuk. Nazywa się to pchnięciem nienasycającym lub nienasycającym .

Relabel

Operacja zbrojenia dotyczy węzła aktywnego $u$ bez żadnych dopuszczalnych odstępów w $G f$ . Modyfikuje $𝓁 (u) tak,$ aby była wartością minimalną, tak że powstaje dopuszczalny łuk zewnętrzny. Zauważ, że to zawsze zwiększa $𝓁 (u)$ i nigdy nie tworzy stromego łuku, który jest łukiem $(u, v)$ takim, że $c f (u, v)> 0$ i $𝓁 (u)> 𝓁 (v) + 1$ .

relabel(u):
    assert x_f[u] > 0 and 𝓁[u] <= 𝓁[v] for all v such that c_f[u][v] > 0
    𝓁[u] = 1 + min(𝓁[v] for all v such that c_f[u][v] > 0)

Skutki popychania i relabelowania

Po operacji wypychania lub $zmiany$ etykiety $𝓁$ pozostaje ważną funkcją etykietowania w odniesieniu do $f$ .

Dla operacji pchania na dopuszczalnym łuku $(u, v)$ , może dodać łuk $(v, u)$ do $E f$ , gdzie $𝓁 (v) = 𝓁 (u) - 1 \leq 𝓁 (u) + 1$ ; może również usunąć łuk $(u, v)$ z $E f$ , gdzie skutecznie usuwa wiązanie $𝓁 (u) \leq 𝓁 (v) + 1$ .

Aby zobaczyć, że operacja zmiany $etykiety$ na węźle $u$ zachowuje ważność $𝓁 (u)$ , zauważ, że jest to trywialnie gwarantowane przez definicję dla wyjść u w $G f$ . Dla łuków $u$ w $G f$ , zwiększone $𝓁 (u)$ może tylko mniej ściśle spełniać ograniczenia, a nie je naruszać.

Ogólny algorytm push-relabel

Ogólny algorytm wypychania i ponownego etykietowania służy wyłącznie jako dowód słuszności koncepcji i nie zawiera szczegółów implementacji dotyczących sposobu wybierania aktywnego węzła do operacji wypychania i ponownego etykietowania. Ta ogólna wersja algorytmu kończy się na $O (V 2 E)$ .

Ponieważ $𝓁 (s) = | V |$ , $𝓁 (t) = 0$ i nie ma ścieżek dłuższych niż $| V | - 1$ w $G f$ , aby $𝓁 (s)$ spełniały ważny warunek na etykiecie, $s$ muszą być odłączone od $t$ . Podczas inicjalizacji algorytm spełnia to wymaganie, tworząc przepływ wstępny $f,$ który nasyca wszystkie wyjścia łukowe $s$ , po czym $𝓁 (v) = 0$ jest trywialnie ważne dla wszystkich $v ∈ V \ { s , t }$ . Po inicjalizacji algorytm wielokrotnie wykonuje odpowiednią operację wypychania lub zmiany etykiety, aż żadna z takich operacji nie ma zastosowania, w którym to momencie wstępny przepływ został przekształcony w przepływ maksymalny.

generic-push-relabel(G, c, s, t):
    create a pre-flow f that saturates all out-arcs of s
    let 𝓁[s] = |V|
    let 𝓁[v] = 0 for all v ∈ V \ {s}
    while there is an applicable push or relabel operation do
        execute the operation

Poprawność

Algorytm zachowuje warunek, że $𝓁$ jest prawidłowym etykietowaniem podczas jego wykonywania. Można to udowodnić, badając wpływ operacji wypychania i ponownego etykietowania na funkcję etykiety $𝓁$ . Operacja zmiany etykiety zwiększa wartość etykiety o powiązane minimum plus jeden, co zawsze będzie spełniało ograniczenie $𝓁 (u) \leq 𝓁 (v) + 1$ . Operacja wypychania może wysłać przepływ od $u$ do $v,$ jeśli $𝓁 (u) = 𝓁 (v) + 1$ . To może dodać $(v, u)$ do $G f$ i może usunąć $(u, v)$ z $G f$ . Dodanie $(v, u)$ do $G f$ nie wpłynie na prawidłowe oznakowanie, ponieważ $𝓁 (v) = 𝓁 (u) - 1$ . Usunięcie $(u, v)$ z $G f$ usuwa odpowiednie ograniczenie, ponieważ prawidłowa właściwość etykietowania $𝓁 (u) \leq 𝓁 (v) + 1$ dotyczy tylko łuków resztkowych w $G f$ .

Jeśli istnieje przepływ wstępny $fi$ ważne oznakowanie $𝓁$ dla $f$ , to nie ma ścieżki rozszerzającej od $s$ do $t$ na wykresie reszt $G f$ . Można to udowodnić poprzez sprzeczność opartą na nierównościach, które pojawiają się w funkcji etykietowania, gdy zakłada się, że istnieje ścieżka zwiększająca się. Jeśli algorytm się kończy, to wszystkie węzły w $V \ { s , t }$ nie są aktywne. Oznacza to, że wszystkie $v ∈ V \ { s , t }$ nie mają nadmiernego przepływu, a bez nadmiaru przepływ wstępny $f jest$ zgodny z ograniczeniem zachowania przepływu i można go uznać za normalny przepływ. Przepływ ten jest maksymalnym przepływem zgodnie z twierdzeniem o maksymalnym przepływie i minimalnym cięciu, ponieważ nie ma ścieżki zwiększającej się od $s$ do $t$ .

Dlatego algorytm zwróci maksymalny przepływ po zakończeniu.

Złożoność czasowa

Aby ograniczyć złożoność czasową algorytmu, musimy przeanalizować liczbę operacji wypychania i ponownego etykietowania, które występują w głównej pętli. Liczby operacji zmiany etykiety, wypychania nasycającego i wypychania nienasycającego są analizowane oddzielnie.

W algorytmie operację ponownego oznaczenia można wykonać co najwyżej $(2 | V | - 1) (| V | - 2) <2 | V | 2$ razy. Dzieje się tak, ponieważ wartość etykiety $𝓁 (u)$ dla dowolnego węzła u nigdy nie może spaść, a maksymalna wartość etykiety wynosi co najwyżej $2 | V | - 1$ dla wszystkich węzłów. Oznacza to, że operacja zmiany etykiety może zostać potencjalnie wykonana $2 | V | - 1$ razy dla wszystkich węzłów $V \ { s , t }$ (tj. $| V | - 2$ ). Powoduje to ograniczenie $O (V 2)$ dla operacji zbrojenia.

Każde nasycające naciśnięcie dopuszczalnego łuku $(u, v)$ usuwa łuk z $G f$ . Aby łuk mógł zostać ponownie wstawiony do $G f w$ celu kolejnego nasycenia pchnięcia, najpierw należy ponownie oznaczyć $v$ , a następnie nacisnąć łuk $(v, u)$ , a następnie $u$ musi zostać ponownie oznaczony. W tym procesie $𝓁 (u)$ wzrasta o co najmniej dwa. Dlatego występują pchnięcia nasycające $O (V)$ włączone $(u, v)$ , a całkowita liczba pchnięć nasycających wynosi co najwyżej $2 | V || E |$ . Powoduje to ograniczenie czasu $O (VE)$ dla operacji wypychania nasycającego.

Ograniczenie liczby nienasyconych pchnięć można osiągnąć za pomocą potencjalnego argumentu . Używamy funkcji potencjału $Φ = \sum [u \in V \land x f (u)> 0] 𝓁 (u)$ (tj. $Φ$ jest sumą etykiet wszystkich aktywnych węzłów). Jest oczywiste, że $Φ$ początkowo wynosi $0$ i pozostaje nieujemne przez cały czas wykonywania algorytmu. Zarówno ponowne etykiety, jak i nasycające wypchnięcia mogą wzrosnąć $Φ$ . Jednak wartość $Φ$ musi być równa 0 w momencie zakończenia, ponieważ na końcu wykonywania algorytmu nie może być żadnych pozostałych aktywnych węzłów. Oznacza to, że w trakcie wykonywania algorytmu wypychanie nienasycające musi stanowić różnicę operacji wypychania zmiennego i wypychania nasycającego, aby $Φ$ zakończyło się wartością 0. Operacja zmiany etykiety może wzrosnąć $Φ$ co najwyżej $(2 | V | - 1) (| V | - 2)$ . Nasycające pchnięcie $(u, v)$ aktywuje $v,$ jeśli było nieaktywne przed pchnięciem, zwiększając $Φ$ co najwyżej o $2 | V | - 1$ . Stąd całkowity wkład wszystkich operacji wypychania nasycającego do $Φ$ wynosi co najwyżej $(2 | V | - 1) (2 | V || E |)$ . Naciśnięcie nienasycające $(u, v)$ zawsze dezaktywuje $u$ , ale może również aktywować $v,$ jak w przypadku naciśnięcia nasycającego. W rezultacie zmniejsza się $Φ$ o co najmniej $𝓁 (u) - 𝓁 (v) = 1$ . Ponieważ ponowne etykiety i wypchnięcia nasycające wzrastają $Φ$ , całkowita liczba nienasyconych wypchnięć musi stanowić różnicę $(2 | V | - 1) (| V | - 2) + (2 | V | - 1) (2 | V || E |) \leq 4 | V | 2 | E |$ . Powoduje to ograniczenie czasu $O (V 2 E)$ dla nienasycających operacji wypychania.

Podsumowując, algorytm wykonuje ponowne etykiety $O (V 2),$ przepychania nasycające $O (VE)$ i wypychania nienasycające $O (V 2 E)$ . Struktury danych mogą być zaprojektowane tak, aby wybrać i wykonać odpowiednią operację w czasie $O (1)$ . Dlatego złożoność czasowa algorytmu wynosi $O (V 2 E)$ .

Przykład

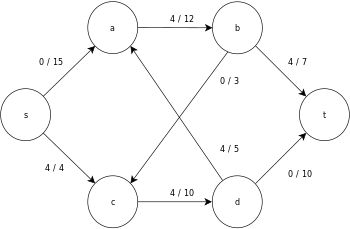
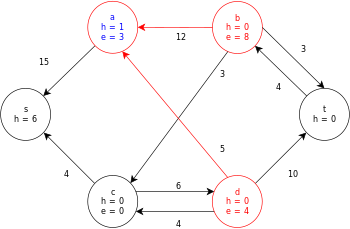
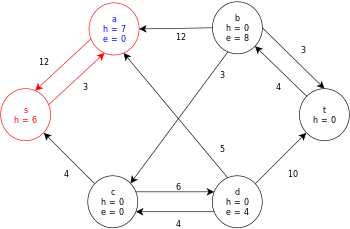
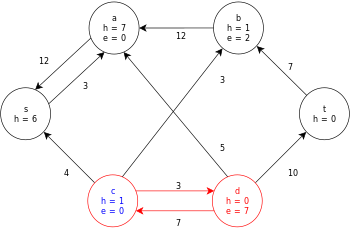
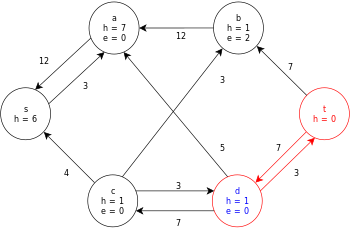
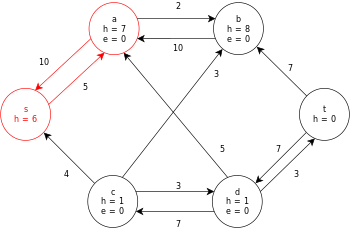
Poniżej przedstawiono przykładowe wykonanie ogólnego algorytmu push-relabel, zgodnie z powyższą definicją, na poniższym prostym diagramie graficznym przepływu sieci.

Początkowy wykres sieci przepływu

Końcowy wykres sieci maksymalnego przepływu

W tym przykładzie wartości h i e oznaczają odpowiednio etykietę $𝓁$ i nadmiar $x f$ węzła podczas wykonywania algorytmu. Każdy wykres szczątkowy w przykładzie zawiera tylko łuki szczątkowe o pojemności większej od zera. Każdy wykres resztkowy może zawierać wiele iteracji pętli wykonywania operacji .

Operacje algorytmu	Wykres reszt
Zainicjuj wykres pozostałości, ustawiając przepływ wstępny na wartości 0 i inicjalizując etykietowanie.
Wstępne wypychanie nasycające jest wykonywane na wszystkich łukach przed wypływem ze źródła, $s$ .
Węzeł $a$ zostaje ponownie oznakowany, aby przepchnąć jego nadmiar w kierunku zlewu, $t$ . Nadmiar w $a$ jest następnie wypychany do $b,$ a następnie $d$ w dwóch kolejnych nasycających naciśnięciach ; który nadal pozostawia z pewnym nadmiarem.

Ponownie $a$ jest ponownie oznaczane, aby przesunąć jego nadmiar wzdłuż ostatniej pozostałej dodatniej pozostałości (tj. Przesunąć nadmiar z powrotem do $s$ ). Węzeł $a$ jest następnie usuwany ze zbioru aktywnych węzłów.

Zmień etykietę $b,$ a następnie przesuń jego nadmiar do $t$ i $c$ .
Ponownie oznacz $c,$ a następnie przesuń jego nadmiar do $d$ .
Ponownie oznacz $d,$ a następnie przesuń jego nadmiar do $t$ .
To pozostawia węzeł $b$ jako jedyny pozostały aktywny węzeł, ale nie może popchnąć nadmiaru przepływu w kierunku zlewu. Zmień etykietę $b,$ a następnie popchnij jego nadmiar w kierunku źródła $s$ przez węzeł $a$ .

Wepchnij ostatni kawałek nadmiaru $z$ powrotem do źródła, $s$ . Nie ma pozostałych aktywnych węzłów. Algorytm kończy działanie i zwraca maksymalny przepływ wykresu (jak widać powyżej).

Przykład (ale z początkowym przepływem 0) można uruchomić tutaj interaktywnie.

Praktyczne wdrożenia

Podczas gdy ogólny algorytm push-relabel ma złożoność czasową $O (V 2 E)$ , wydajne implementacje osiągają $O (V 3)$ lub niższą złożoność czasową poprzez wymuszanie odpowiednich reguł wyboru odpowiednich operacji wypychania i ponownego etykietowania. Wydajność empiryczną można dodatkowo ulepszyć dzięki heurystyce.

Struktura danych „prąd łukowy” i operacja wyładowania

Struktura danych „prąd łukowy” jest mechanizmem odwiedzania sąsiadów wchodzących i wychodzących z węzła w sieci przepływowej w statycznej, cyklicznej kolejności. Jeśli pojedynczo połączona lista sąsiadów jest tworzona dla węzła, struktura danych może być tak prosta, jak wskaźnik do listy, która przechodzi przez listę i przewija się do początku, gdy kończy się.

Na podstawie struktury danych „prąd łukowy” można zdefiniować operację rozładowania. Operacja wyładowania jest wykonywana na aktywnym węźle i wielokrotnie wypycha przepływ z węzła, aż stanie się on nieaktywny, zmieniając etykietę w razie potrzeby, aby utworzyć dopuszczalne łuki w procesie.

discharge(u):
    while x_f[u] > 0 do
        if current-arc[u] has run off the end of neighbors[u] then
            relabel(u)
            rewind current-arc[u]
        else
            let (u, v) = current-arc[u]
            if (u, v) is admissible then
                push(u, v)
            let current-arc[u] point to the next neighbor of u

Reguły wyboru aktywnych węzłów

Zdefiniowanie operacji rozładowania ogranicza algorytm wypychania-ponownego etykietowania do wielokrotnego wybierania aktywnego węzła do rozładowania. W zależności od reguły wyboru algorytm wykazuje różną złożoność czasową. Ze względu na zwięzłość pomijamy $s$ i $t$ , odnosząc się do węzłów w poniższej dyskusji.

Reguła wyboru FIFO

FIFO algorytm push relabel organizuje aktywnych węzłów w kolejce. Początkowe aktywne węzły można wstawiać w dowolnej kolejności. Algorytm zawsze usuwa węzeł z przodu kolejki do rozładowania. Za każdym razem, gdy nieaktywny węzeł staje się aktywny, jest dołączany z tyłu kolejki.

Algorytm ma złożoność czasową $O (V 3)$ .

Reguła wyboru przeniesienia etykiety na wierzch

Algorytm relabel-to-front push-relabel organizuje wszystkie węzły w połączoną listę i utrzymuje niezmiennik, że lista jest topologicznie posortowana w odniesieniu do dopuszczalnej sieci. Algorytm skanuje listę od początku do końca i wykonuje operację wyładowania na bieżącym węźle, jeśli jest on aktywny. Jeśli nazwa węzła zostanie zmieniona, zostanie przeniesiony na początek listy, a skanowanie zostanie wznowione od początku.

Algorytm ma również złożoność czasową $O (V 3)$ .

Najwyższa reguła wyboru etykiety

Algorytm push-relabel o najwyższej etykiecie organizuje wszystkie węzły w zasobniki indeksowane według ich etykiet. Algorytm zawsze wybiera aktywny węzeł z największą etykietą do rozładowania.

Algorytm ma złożoność czasową $O (V 2 \sqrt E)$ . Jeśli zamiast tego stosowana jest reguła wyboru o najniższej etykiecie, złożoność czasowa staje się $O (V 2 E)$ .

Techniki wdrożeniowe

Chociaż w opisie ogólnego algorytmu push- $relabel$ powyżej, $𝓁 ($ $u$ $)$ jest ustawione na zero dla każdego węzła u innego niż $s$ i $t$ na początku, lepiej jest przeprowadzić przeszukiwanie wstecz wszerz od $t,$ aby obliczyć dokładnie etykiety.

Algorytm jest zwykle podzielony na dwie fazy. Faza pierwsza oblicza maksymalny przepływ wstępny poprzez rozładowanie tylko aktywnych węzłów, których etykiety są poniżej $n$ . Faza druga przekształca maksymalny przepływ wstępny w przepływ maksymalny poprzez zawracanie nadmiaru przepływu, który nie może osiągnąć $t$ do $s$ . Można wykazać, że faza druga ma złożoność czasową $O (VE)$ niezależnie od kolejności operacji wypychania i zmiany etykiety, a zatem jest zdominowana przez fazę pierwszą. Alternatywnie można to zaimplementować za pomocą dekompozycji przepływu.

Heurystyki mają kluczowe znaczenie dla poprawy empirycznej wydajności algorytmu. Dwie powszechnie stosowane heurystyki to heurystyka luk i heurystyka globalnego ponownego etykietowania. Heurystyka luk wykrywa luki w funkcji etykietowania. Jeśli istnieje etykieta 0 <𝓁 ' <| V | dla którego nie ma węzła $u$ takiego, że $𝓁 (u) = 𝓁'$ , to dowolny węzeł $u$ z $𝓁' <𝓁 (u) <| V |$ został odłączony od $t$ i może zostać natychmiast zmieniony na $(| V | + 1)$ . Globalna heurystyka ponownego etykietowania okresowo wykonuje przeszukiwanie wstecz wszerz od $t$ w $G f,$ aby obliczyć dokładne etykiety węzłów. Obie heurystyki pomijają nieprzydatne operacje relabelowania, które są wąskim gardłem algorytmu i przyczyniają się do nieefektywności drzew dynamicznych.

Przykładowe realizacje

C implementacja

#include <stdlib.h>
#include <stdio.h>

#define NODES 6
#define MIN(X,Y) ((X) < (Y) ? (X) : (Y))
#define INFINITE 10000000

void push(const int * const * C, int ** F, int *excess, int u, int v) {
  int send = MIN(excess[u], C[u][v] - F[u][v]);
  F[u][v] += send;
  F[v][u] -= send;
  excess[u] -= send;
  excess[v] += send;
}

void relabel(const int * const * C, const int * const * F, int *height, int u) {
  int v;
  int min_height = INFINITE;
  for (v = 0; v < NODES; v++) {
    if (C[u][v] - F[u][v] > 0) {
      min_height = MIN(min_height, height[v]);
      height[u] = min_height + 1;
    }
  }
};

void discharge(const int * const * C, int ** F, int *excess, int *height, int *seen, int u) {
  while (excess[u] > 0) {
    if (seen[u] < NODES) {
      int v = seen[u];
      if ((C[u][v] - F[u][v] > 0) && (height[u] > height[v])) {
        push(C, F, excess, u, v);
      } else {
        seen[u] += 1;
      }
    } else {
      relabel(C, F, height, u);
      seen[u] = 0;
    }
  }
}

void moveToFront(int i, int *A) {
  int temp = A[i];
  int n;
  for (n = i; n > 0; n--) {
    A[n] = A[n-1];
  }
  A[0] = temp;
}

int pushRelabel(const int * const * C, int ** F, int source, int sink) {
  int *excess, *height, *list, *seen, i, p;

  excess = (int *) calloc(NODES, sizeof(int));
  height = (int *) calloc(NODES, sizeof(int));
  seen = (int *) calloc(NODES, sizeof(int));

  list = (int *) calloc((NODES-2), sizeof(int));

  for (i = 0, p = 0; i < NODES; i++){
    if ((i != source) && (i != sink)) {
      list[p] = i;
      p++;
    }
  }

  height[source] = NODES;
  excess[source] = INFINITE;
  for (i = 0; i < NODES; i++)
    push(C, F, excess, source, i);

  p = 0;
  while (p < NODES - 2) {
    int u = list[p];
    int old_height = height[u];
    discharge(C, F, excess, height, seen, u);
    if (height[u] > old_height) {
      moveToFront(p, list);
      p = 0;
    } else {
      p += 1;
    }
  }
  int maxflow = 0;
  for (i = 0; i < NODES; i++)
    maxflow += F[source][i];

  free(list);

  free(seen);
  free(height);
  free(excess);

  return maxflow;
}

void printMatrix(const int * const * M) {
  int i, j;
  for (i = 0; i < NODES; i++) {
    for (j = 0; j < NODES; j++)
      printf("%d\t",M[i][j]);
    printf("\n");
  }
}

int main(void) {
  int **flow, **capacities, i;
  flow = (int **) calloc(NODES, sizeof(int*));
  capacities = (int **) calloc(NODES, sizeof(int*));
  for (i = 0; i < NODES; i++) {
    flow[i] = (int *) calloc(NODES, sizeof(int));
    capacities[i] = (int *) calloc(NODES, sizeof(int));
  }

  // Sample graph
  capacities[0][1] = 2;
  capacities[0][2] = 9;
  capacities[1][2] = 1;
  capacities[1][3] = 0;
  capacities[1][4] = 0;
  capacities[2][4] = 7;
  capacities[3][5] = 7;
  capacities[4][5] = 4;

  printf("Capacity:\n");
  printMatrix(capacities);

  printf("Max Flow:\n%d\n", pushRelabel(capacities, flow, 0, 5));

  printf("Flows:\n");
  printMatrix(flow);

  return 0;
}

Implementacja Pythona

def relabel_to_front(C, source: int, sink: int) -> int:
    n = len(C)  # C is the capacity matrix
    F = [[0] * n for _ in range(n)]
    # residual capacity from u to v is C[u][v] - F[u][v]

    height = [0] * n  # height of node
    excess = [0] * n  # flow into node minus flow from node
    seen   = [0] * n  # neighbours seen since last relabel
    # node "queue"
    nodelist = [i for i in range(n) if i != source and i != sink]

    def push(u, v):
        send = min(excess[u], C[u][v] - F[u][v])
        F[u][v] += send
        F[v][u] -= send
        excess[u] -= send
        excess[v] += send

    def relabel(u):
        # Find smallest new height making a push possible,
        # if such a push is possible at all.
        min_height = ∞
        for v in xrange(n):
            if C[u][v] - F[u][v] > 0:
                min_height = min(min_height, height[v])
                height[u] = min_height + 1

    def discharge(u):
        while excess[u] > 0:
            if seen[u] < n:  # check next neighbour
                v = seen[u]
                if C[u][v] - F[u][v] > 0 and height[u] > height[v]:
                    push(u, v)
                else:
                    seen[u] += 1
            else:  # we have checked all neighbours. must relabel
                relabel(u)
                seen[u] = 0

    height[source] = n  # longest path from source to sink is less than n long
    excess[source] = ∞  # send as much flow as possible to neighbours of source
    for v in range(n):
        push(source, v)

    p = 0
    while p < len(nodelist):
        u = nodelist[p]
        old_height = height[u]
        discharge(u)
        if height[u] > old_height:
            nodelist.insert(0, nodelist.pop(p))  # move to front of list
            p = 0  # start from front of list
        else:
            p += 1

    return sum(F[source])

Languages

In other projects