Specker sekwencja - Specker sequence

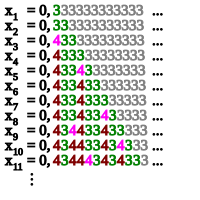
Sekwencja Specker. N p cyfry x k wynosi 4 , gdy n ≤ K i obliczenie { n } ( n ) zatrzymuje się po k etapach; w przeciwnym razie jest 3 .

W teoria obliczalności , A sekwencja Specker jest obliczalny , monotonicznie rosnącą, ograniczony sekwencja liczb wymiernych którego Supremum nie jest obliczalny liczba rzeczywista . Pierwszym przykładem takiej sekwencji skonstruowano przez Ernst Specker (1949).

Istnienie sekwencji Specker ma konsekwencje dla analizy obliczeniowego . Fakt, że takie sekwencje istnieją oznacza, że zbiór wszystkich liczb rzeczywistych obliczalnych nie spełnia kres górny zasadę rzeczywistej analizy, nawet biorąc pod uwagę tylko obliczalne sekwencje. Częstym sposobem rozwiązania tej trudności jest wzięcie pod uwagę tylko sekwencje, które towarzyszą przez moduł konwergencji ; Nie ma sekwencję Specker obliczalną moduł zbieżności.

Przynajmniej górna zasada związana również analizowano w programie odwróconej matematycznych , w których dokładne wytrzymałość tej zasady zostało ustalone. W nomenklaturze tego programu, zasada najmniej górna granica odpowiada ACA 0 przez RCA 0 .

Budowa

Poniższa konstrukcja jest opisana przez Kushner (1984). Niech być dowolny rekurencyjnie przeliczalny zbiór liczb naturalnych, które nie jest rozstrzygalne i niech ( I ) być obliczalny wyliczanie A bez powtórzeń. Określić sekwencję ( q n ) liczb wymiernych z zasadą

Jest oczywiste, że każdy Q n jest dodatnią i racjonalne, a sekwencja Q n jest ściśle wzrasta. Ponadto, ponieważ i ma powtórzeń, możliwe jest oszacowanie każdego q n przeciwko serii

Zatem sekwencja ( q n ) jest ograniczony od góry przez klasycznie 1. Oznacza to, że P n ma Supremum X .

Wykazano, że x nie jest obliczalny liczbą rzeczywistą. Dowodem wykorzystuje konkretny fakt o obliczalnych liczb rzeczywistych. Jeśli x były obliczeniowy wtedy nie byłby obliczeniowy funkcja r ( n ) w taki sposób, że | q j - q I | <1 / N dla wszystkich i , j > r ( n ). Aby obliczyć R , porównaj binarnego rozszerzenie X z binarnym ekspansji q i większych i dużych wartości I . Określenie Q i powoduje cyfrę binarną przejść od 0 do 1, za każdym razem I zwiększona o 1. W ten sposób będzie kilka n gdzie wystarczająco duży początkowy odcinek X jest już określony przez q n , że bez dodatkowych cyfr binarnych w segment ten może zawsze być włączony, co prowadzi do oszacowania odległości pomiędzy q ı i q j o ı , j > N .

Jeśli jakakolwiek taka funkcja R były obliczalne, prowadziłoby to do postępowania decyzyjnego dla A , w następujący sposób. Biorąc pod uwagę wejście k , obliczyć r (2 k +1 ). Zauważ, że jeśli k były wyświetlane w kolejności ( í ), to spowodowałoby sekwencję ( q I ) zwiększy się o 2 - k -1 , ale to nie może się zdarzyć, gdy wszystkie elementy ( q I ) są w ciągu 2 - k -1 od siebie. Tak więc, jeśli k będzie wyliczone na na I , musi być wyliczone dla wartości I mniej niż R (2 k + 1 ). Pozostawia skończoną liczbę możliwych miejscach, gdzie k mogą być wymienione. Aby zakończyć procedurę decyzyjną, sprawdzić je w sposób efektywny i powrotu 0 lub 1 w zależności od tego, czy k znaleziono.

Zobacz też

Referencje

  • Douglas Mosty i Fred Richman. Odmiany konstruktywną Matematyki, Oxford, 1987.
  • BA Kushner (1984), Wykłady z analizy matematycznej konstruktywnej American Mathematical Society, przekłady Monografie Matematyczne v. 60.
  • Jakoba Simonsen G. (2005), "sekwencja Specker revisited", matematyczne logicznego Quarterly , t. 51, str. 532-540. doi : 10,1002 / malq.200410048
  • S. Simpson (1999), Podsystemy drugiego rzędu arytmetycznych , Springer.
  • E. Specker (1949), "Nicht Konstruktiv beweisbare Sätze der Analysis" Journal symbolicznego logiki , t. 14, str. 145-158.