Ośrodek homotyczny - Homothetic center

Rysunek 1: Punkt O jest zewnętrznym środkiem homotycznym dla dwóch trójkątów. Wielkość każdej figury jest proporcjonalna do jej odległości od środka homotetycznego.

W geometrii , A homothetic centrum (zwany również środek podobieństwa lub środka podobieństwo ) jest punkt, z których co najmniej dwie geometrycznie podobne dane mogą być postrzegane jako rozszerzania lub kurczenia się od siebie. Jeśli środek jest na zewnątrz , dwie figury są do siebie bezpośrednio podobne; ich kąty mają ten sam zwrot obrotu. Jeśli środek jest wewnętrzny , dwie figury są swoimi skalowanymi odbiciami lustrzanymi; ich kąty mają odwrotny sens.

Figura 2: Dwie figury geometryczne związane z zewnętrznego homothetic środkowej S . Kąty w odpowiednich punktach są takie same i mają ten sam sens; na przykład kąty ABC i A'B'C 'są zgodne z ruchem wskazówek zegara i równe pod względem wielkości.

Ogólne wielokąty

Zewnętrzne (powyżej) i wewnętrzne (poniżej) homotetyczne środki obu kół (czerwony) są pokazane jako czarne punkty.

Jeśli dwie figury geometryczne posiadają homothetic środek, są podobne do siebie nawzajem; innymi słowy, muszą mieć te same kąty w odpowiednich punktach i różnić się jedynie względnym skalowaniem. Środek homotyczny i dwie figury nie muszą leżeć na tej samej płaszczyźnie; można je powiązać rzutem z centrum homotetycznego.

Ośrodki homotetyczne mogą być zewnętrzne lub wewnętrzne. Jeśli środek jest wewnętrzny, dwie figury geometryczne są swoimi skalowanymi lustrzanymi odbiciami; w języku technicznym mają przeciwną chiralność . Kąt zgodny z ruchem wskazówek zegara na jednej figurze odpowiadałby kątowi w kierunku przeciwnym do ruchu wskazówek zegara na drugiej. I odwrotnie, jeśli środek jest na zewnątrz, dwie figury są do siebie bezpośrednio podobne; ich kąty mają ten sam sens.

Kręgi

Okręgi są geometrycznie do siebie podobne i lustrzanie symetryczne. Stąd para okręgów ma oba typy centrów homotycznych, wewnętrzne i zewnętrzne, chyba że centra są równe lub promienie są równe; te wyjątkowe przypadki są rozpatrywane według ogólnego stanowiska . Te dwa homotetyczne centra leżą na linii łączącej środki dwóch danych okręgów, nazywanej linią centrów (ryc. 3). Można również uwzględnić okręgi o promieniu zerowym (patrz wyjątkowe przypadki), a także użyć ujemnego promienia, przełączając zewnętrzne i wewnętrzne.

Obliczanie centrów homotycznych

Rysunek 3: Dwa koła mają oba typy centrów homotycznych, wewnętrzne ( I ) i zewnętrzne ( E ). Promienie okręgów ( r ₁ i r ₂ ) są proporcjonalne do odległości (d) od każdego środka homotetycznego. Punkty A ₁ i A ₂ są homologiczne, podobnie jak punkty B ₁ i B ₂ .

Dla danej pary okręgów wewnętrzne i zewnętrzne centra homotetyczne można znaleźć na różne sposoby. W geometrii analitycznej wewnętrzny homotetyczny środek jest średnią ważoną środków kół, ważoną promieniem przeciwległego koła - odległość od środka koła do środka wewnętrznego jest proporcjonalna do tego promienia, więc ważenie jest proporcjonalne do przeciwnego promienia. Oznaczając środki okręgów i przez i oraz ich promienie przez i i oznaczając środek przez to: ${\ displaystyle C_ {1}}$ ${\ displaystyle C_ {2}}$ ${\ displaystyle (x_ {1}, y_ {1})}$ ${\ displaystyle (x_ {2}, y_ {2})}$ ${\ displaystyle r_ {1}}$ ${\ displaystyle r_ {2}}$ ${\ displaystyle (x_ {0}, y_ {0}),}$

{\ Displaystyle (x_ {0}, y_ {0}) = {\ Frac {r_ {2}} {r_ {1} + r_ {2}}} (x_ {1}, y_ {1}) + {\ frac {r_ {1}} {r_ {1} + r_ {2}}} (x_ {2}, y_ {2}).}

Środek zewnętrzny można obliczyć za pomocą tego samego równania, ale biorąc pod uwagę jeden z promieni jako ujemny; jeden z nich daje to samo równanie, które jest:

{\ Displaystyle (x_ {e}, y_ {e}) = {\ Frac {-r_ {2}} {r_ {1} -r_ {2}}} (x_ {1}, y_ {1}) + { \ frac {r_ {1}} {r_ {1} -r_ {2}}} (x_ {2}, y_ {2}).}

Mówiąc bardziej ogólnie, biorąc oba promienie z tym samym znakiem (dodatnie lub oba ujemne) daje środek wewnętrzny, podczas gdy przyjmowanie promieni o przeciwnych znakach (jeden dodatni, a drugi ujemny) daje środek zewnętrzny. Zauważ, że równanie dla środka wewnętrznego jest ważne dla dowolnych wartości (chyba że oba promienie zero lub jeden jest ujemny dla drugiego), ale równanie dla środka zewnętrznego wymaga, aby promienie były różne, w przeciwnym razie wymaga dzielenia przez zero.

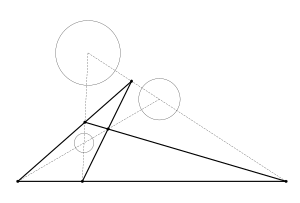
W geometrii syntetycznej rysuje się dwie równoległe średnice, po jednej dla każdego okręgu; tworzą one ten sam kąt α z linią środków. Proste A ₁A ₂ i B ₁B ₂ poprowadzone przez odpowiednie punkty końcowe tych promieni, które są punktami homologicznymi, przecinają się nawzajem oraz linię środków w zewnętrznym środku homotetycznym. I odwrotnie, linie A ₁B ₂ i B ₁A ₂ przechodzące przez jeden punkt końcowy i przeciwny punkt końcowy jego odpowiednika przecinają się wzajemnie, a linia środków w wewnętrznym centrum homotetycznym.

Ograniczającym przypadkiem tej konstrukcji jest linia styczna do obu okręgów (linia bitangensy) przechodząca przez jeden z centrów homotycznych, ponieważ tworzy kąty proste z obydwoma odpowiadającymi średnicami, które są więc równoległe; zobacz styczne do dwóch okręgów, aby uzyskać szczegółowe informacje. Jeśli okręgi spadają po przeciwnych stronach linii, przechodzi ona przez wewnętrzny środek homotyczny, jak w A ₂B ₁ na powyższym rysunku. I odwrotnie, jeśli okręgi leżą po tej samej stronie linii, przechodzi ona przez zewnętrzny środek homotyczny (nie pokazano).

Przypadki specjalne

Jeśli okręgi mają ten sam promień (ale różne centra), nie mają one zewnętrznego środka homotetycznego w płaszczyźnie afinicznej : w geometrii analitycznej powoduje to podział przez zero, natomiast w geometrii syntetycznej proste i równoległe do linii środków (oba dla siecznych i bitangensów) i dlatego nie mają przecięcia. Środek zewnętrzny można zdefiniować na płaszczyźnie rzutowej jako punkt w nieskończoności odpowiadający nachyleniu tej linii. Jest to również granica zewnętrznego środka, jeśli środki okręgów są stałe, a promienie są zmieniane, aż będą równe. ${\ displaystyle A_ {1} A_ {2}}$ ${\ displaystyle B_ {1} B_ {2}}$

Jeśli okręgi mają ten sam środek, ale różne promienie, zarówno zewnętrzny, jak i wewnętrzny pokrywają się ze wspólnym środkiem okręgów. Można to zobaczyć na podstawie wzoru analitycznego, a także jest to granica dwóch centrów homotetycznych, ponieważ środki dwóch okręgów są zmieniane, aż się pokrywają, utrzymując równe promienie. Nie ma jednak linii środków, a syntetyczna konstrukcja zawodzi, ponieważ dwie równoległe linie pokrywają się.

Jeśli jeden promień jest równy zero, a drugi jest niezerowy (punkt i okrąg), zarówno zewnętrzny, jak i wewnętrzny środek pokrywają się z punktem (środek okręgu o promieniu zero).

Jeśli oba okręgi są identyczne (ten sam środek, ten sam promień), środek wewnętrzny jest ich wspólnym środkiem, ale nie ma dobrze zdefiniowanego środka zewnętrznego - właściwie funkcja od przestrzeni parametrów dwóch okręgów w płaszczyźnie do środka zewnętrznego ma nieusuwalną nieciągłość w miejscu identycznych okręgów. W granicy dwóch okręgów o tym samym promieniu, ale różnych środkach zmierzających do posiadania tego samego środka, środek zewnętrzny jest punktem w nieskończoności odpowiadającym nachyleniu linii środków, który może być dowolny, więc nie ma ograniczeń dla wszystkich możliwych pary takich kręgów.

I odwrotnie, jeśli oba promienie są równe zero (dwa punkty), ale punkty są różne, środek zewnętrzny można zdefiniować jako punkt w nieskończoności odpowiadający nachyleniu linii środków, ale nie ma dobrze określonego środka wewnętrznego.

Punkty homologiczne i antyhomologiczne

Rysunek 4: Linie przechodzące przez odpowiednie punkty antyhomologiczne przecinają się na osi radykalnej dwóch danych okręgów (zielonego i niebieskiego). Punkty Q i P ′ są antyhomologiczne, podobnie jak S i R ′ . Te cztery punkty leżą na okręgu, który przecina dwa dane okręgi; linie przechodzące przez punkty przecięcia nowego okręgu z dwoma podanymi okręgami muszą przecinać się w radykalnym środku G trzech okręgów, który leży na osi radykalnej dwóch danych okręgów.

Ogólnie rzecz biorąc, promień wychodzący z homotetycznego centrum przecina każdy z jego okręgów w dwóch miejscach. Z tych czterech punktów, o dwóch mówi się, że są homologiczne, jeśli narysowane do nich promienie tworzą ten sam kąt z linią łączącą środki, np. Punkty Q i Q ′ na rysunku 4. Punkty, które są współliniowe względem środka homotetycznego, ale nie są homologiczne, mówi się, że są antyhomologiczne , np. punkty Q i P ′ na Rysunku 4.

Pary punktów antyhomologicznych leżą na okręgu

Kiedy dwa promienie z tego samego środka homotetycznego przecinają okręgi, każdy zestaw antyhomologicznych punktów leży na okręgu.

Rozważmy trójkąty EQS i EQ'S ′ (Rysunek 4).
Są podobne, ponieważ oba mają wspólny kąt ∠QES = ∠Q'ES ′ i ponieważ E jest środkiem homotetycznym. Z tego podobieństwa wynika, że ∠ESQ = ∠ES′Q ′ = α . Ze względu na twierdzenie o kącie wpisanym ∠EP′R ′ = ∠ES′Q ′ . ∠QSR '= 180 ° -α ponieważ dodatkowy do ∠ESQ . W czworoboku QSR′P ′ ∠QSR ′ + ∠QP′R ′ = 180 ° -α + α = 180 °, co oznacza, że można go wpisać w okrąg . Z twierdzenia o siecznych wynika, że EQ · EP ′ = ES · ER ′. ${\ Displaystyle {\ Frac {EQ} {EQ ^ {\ prime}}} = {\ Frac {ES} {ES ^ {\ prime}}}}$

W ten sam sposób można wykazać, że PRS'Q ′ można wpisać w kółko, a EP · EQ ′ = ER · ES ′.

Dowodem na to jest podobny do wewnętrznego homothetic środkowej I .
PIR ~ P′IR ′, a następnie ∠RPI = ∠IP′R ′ = α . ∠RS′Q ′ = ∠PP′R ′ = α (twierdzenie o kącie wpisanym). Odcinek RQ ′ jest widziany pod tym samym kątem co P i S ′, co oznacza , że R, P, S ′ i Q ′ leżą na okręgu. Następnie z twierdzenia o przecinających się akordach IP · IQ ′ = IR · IS ′. Podobnie QSP'R ′ można wpisać w okrąg, a IQ · IP ′ = IS · IR ′.

Relacja z osią radykalną

Dwa okręgi mają oś radykalną , która jest linią punktów, z których styczne do obu okręgów mają równą długość. Mówiąc bardziej ogólnie, każdy punkt na osi radykalnej ma tę właściwość, że jego moce względem okręgów są równe. Oś radykalna jest zawsze prostopadła do linii środków, a jeśli przecinają się dwa okręgi, ich osią radykalną jest linia łącząca ich punkty przecięcia. Dla trzech okręgów można zdefiniować trzy osie rodnikowe, po jednej dla każdej pary okręgów ( C ₁ / C ₂ , C ₁ / C ₃ i C ₂ / C ₃ ); Co niezwykłe, te trzy radykalne osie przecinają się w jednym punkcie, w radykalnym centrum . Wszystkie styczne poprowadzone od radykalnego środka do trzech okręgów miałyby taką samą długość.

Do znalezienia punktu na osi radykalnej można użyć dowolnych dwóch par punktów antyhomologicznych. Rozważ dwa promienie wychodzące z zewnętrznego centrum homotetycznego E na ryc. 4. Promienie te przecinają dwa dane okręgi (zielony i niebieski na ryc. 4) w dwóch parach punktów antyhomologicznych, Q i P ′ dla pierwszego promienia oraz S i R ′ Dla drugiego promienia. Te cztery punkty leżą na jednym okręgu, który przecina oba podane okręgi. Z definicji prosta QS jest osią radykalną nowego okręgu z zielonym okręgiem, podczas gdy prosta P'R ′ jest osią radykalną nowego okręgu z podanym niebieskim okręgiem. Te dwie proste przecinają się w punkcie G , który jest radykalnym środkiem nowego okręgu i dwóch podanych okręgów. Dlatego punkt G leży również na osi radykalnej dwóch danych okręgów.

Okręgi styczne i punkty antyhomologiczne

Dla każdej pary punktów antyhomologicznych dwóch okręgów istnieje trzeci okrąg, który jest styczny do danych punktów i dotyka ich punktów antyhomologicznych.
Jest też odwrotnie - każdy okrąg, który jest styczny do dwóch innych kręgów, dotyka ich w parze antyhomologicznych punktów.

Rysunek 5: Każdy okrąg, który jest styczny do dwóch podanych okręgów, styka się z nimi w parze antyhomologicznych punktów

Niech nasze dwa okręgi mają środki O ₁ i O ₂ (Ryc. 5). E jest ich zewnętrznym homotetycznym centrum. Konstruujemy dowolny promień z E, który przecina dwa okręgi w P, Q, P ′ i Q ′ . Wydłuż O ₁ Q i O ₂ P ′, aż przecinają się w T ₁ . Łatwo jest udowodnić, że trójkąty O ₁ PQ i O ₂ P′Q ′ są podobne ze względu na homotecję . Są również równoramienne, ponieważ O ₁ P = O ₁ Q ( promień ), więc ∠O ₁ PQ = ∠O ₁ QP = ∠O ₂ P′Q ′ = ∠O ₂ Q′P ′ = ∠T ₁ QP ′ = ∠ T ₁ P′Q . Zatem T ₁ P'Q jest równoramiennego i koło mogą być wykonane z centrum T ₁ i promienia T ₁ P "= t ₁ Q . Ten okrąg jest styczny do dwóch podanych okręgów w punktach Q i P ′ .

Analogiczny jest dowód dla drugiej pary punktów antyhomologicznych ( P i Q ′ ), a także dla wewnętrznego centrum homotetycznego.

Rysunek 6: Rodzina okręgów stycznych dla zewnętrznego środka homotycznego

Rysunek 7: Rodzina okręgów stycznych dla wewnętrznego centrum homotetycznego

Jeśli skonstruujemy kręgi styczne dla każdej możliwej pary punktów antyhomologicznych, otrzymamy dwie rodziny kół - po jednej dla każdego centrum homotycznego. Rodzina okręgów zewnętrznego środka homotetycznego jest taka, że każdy okrąg styczny albo zawiera oba podane okręgi, albo nie zawiera żadnego (ryc. 6). Z drugiej strony okręgi z drugiej rodziny zawsze zawierają tylko jedno z podanych okręgów (rysunek 7).

Rysunek 8: Oś rodnikowa okręgów stycznych przechodzi przez środek rodnika

Wszystkie kręgi z rodziny stycznej mają wspólny ośrodek radykalny, który pokrywa się z ośrodkiem homotetycznym.
Aby to pokazać, rozważ dwa promienie z centrum homotetycznego, przecinające podane okręgi (ryc. 8). Istnieją dwa styczne okręgi T ₁ i T ₂ , które dotykają danych okręgów w punktach antyhomologicznych. Jak już pokazaliśmy, punkty te leżą na okręgu C, a zatem dwa promienie są osiami radykalnymi dla C / T ₁ i C / T ₂ . Wówczas punkt przecięcia dwóch osi rodnikowych musi również należeć do osi rodnikowej T ₁ / T ₂ . Ten punkt przecięcia jest homothetic centrum E .

Jeśli dwa koła styczne dotykają współliniowych par punktu antyhomologicznego - jak na ryc. 5 - to z powodu homotencji . Zatem potęgi E względem dwóch stycznych okręgów są równe, co oznacza, że E należy do osi radykalnej. ${\ Displaystyle {\ Frac {EP} {EP ^ {\ prime}}} = {\ Frac {EQ} {EQ ^ {\ prime}}}; {EP} \ cdot {EQ ^ {\ prime}} = { EQ} \ cdot {EP ^ {\ prime}}}$

Homotetyczne centra trzech kręgów

Każda para okręgów ma dwa centra podobieństwa, dlatego trzy okręgi miałyby sześć centrów podobieństwa, po dwa dla każdej odrębnej pary danych okręgów. Co ciekawe, te sześć punktów leży na czterech liniach, po trzy punkty na każdej linii. Oto jeden sposób, aby to pokazać.

Rysunek 9: W układzie trzech okręgów trzy centra homotetyczne (po jednym na każdą parę okręgów) leżą na jednej linii

Rozważ płaszczyznę trzech okręgów (rysunek 9). Odsuń każdy punkt środkowy prostopadle do płaszczyzny o odległość równą odpowiedniemu promieniu. Środki można odsunąć w dowolną stronę płaszczyzny. Trzy punkty odsunięcia definiują jedną płaszczyznę. Na tej płaszczyźnie tworzymy trzy linie przechodzące przez każdą parę punktów. Linie przebijają płaszczyznę okręgów w punktach H _AB , H _BC i H _AC . Ponieważ zbiór punktów, które są wspólne dla dwóch różnych i nierównoległych płaszczyzn, jest linią, to z konieczności te trzy punkty leżą na takiej prostej. Z podobieństwa trójkątów H _AB AA ′ i H _AB BB ′ widzimy, że ( r _{A, B} to promienie okręgów), a zatem H _AB jest w rzeczywistości homotetycznym środkiem odpowiednich dwóch okręgów. Możemy zrobić to samo dla H _BC i H _AC . ${\ Displaystyle {\ Frac {H_ {AB} B} {H_ {AB} A}} = {\ Frac {r_ {B}} {r_ {A}}}}$

Rysunek 10: Wszystkie sześć centrów homotycznych (kropek) trzech okręgów leży na czterech liniach (grube linie)

Powtórzenie powyższej procedury dla różnych kombinacji centrów homotycznych (w naszej metodzie jest to określone przez stronę, do której odsuwamy środki okręgów) dałoby w sumie cztery linie - trzy centra homotetyczne na każdej linii (Rysunek 10).

Oto kolejny sposób, aby to udowodnić.

Rysunek 11: Niebieska linia to oś rodnikowa dwóch stycznych okręgów C ₁ i C ₂ (różowe). Każda para danych okręgów ma środek homotyczny, który należy do radykalnej osi dwóch stycznych okręgów. Ponieważ oś radykalna jest linią, oznacza to, że trzy centra homotetyczne są współliniowe

Niech C ₁ i C ₂ będą sprzężoną parą okręgów stycznych do wszystkich trzech podanych okręgów (Rysunek 11). Koniugat oznacza, że oba okręgi styczne należą do tej samej rodziny w odniesieniu do jednej z podanych par okręgów. Jak już widzieliśmy, oś radykalna dowolnych dwóch stycznych okręgów z tej samej rodziny przechodzi przez homotetyczne centrum dwóch danych okręgów. Ponieważ koła styczne są wspólne dla wszystkich trzech par danych okręgów następnie ich homothetic ośrodków należą do rodnika osi C ₁ i C ₂ np leżą na jednej linii.

Ta własność jest wykorzystywana w ogólnym rozwiązaniu problemu Apoloniusza Josepha Diaz Gergonne . Biorąc pod uwagę trzy okręgi, można znaleźć centra homotetyczne, a tym samym radykalną oś pary okręgów rozwiązania. Oczywiście istnieje nieskończenie wiele okręgów o tej samej osi radykalnej, więc należy wykonać dodatkową pracę, aby dowiedzieć się, które dokładnie dwa okręgi są rozwiązaniem.

Languages

In other projects