Funkcja znaku zapytania Minkowskiego - Minkowski's question-mark function

Funkcja znaku zapytania Minkowskiego.

Po lewej: ?( x ) . Dobrze: ?( x ) − x .

W matematyce , funkcja Minkowski znak zapytania oznaczone ? ( X ) , to funkcja posiadająca różne nietypowe fraktalne właściwości zdefiniowane przez Hermanna Minkowskiego  ( 1904 , strony 171-172). Mapuje kwadratowe Irrationals do liczb wymiernych na przedział jednostkowy poprzez wyrażenie odnoszącego się do ułamka rozwinięć quadratics do tych binarnych rozszerzenia tych wymiernych, podanych Arnaud Denjoy w 1938. Ponadto, mapuje racjonalne numery dwójkowym wymiernych jako można zobaczyć przez rekurencyjną definicję ściśle związaną z drzewem Sterna-Brocota .

Definicja

Jeśli [ a ₀ ; a ₁ , a ₂ , …] jest reprezentacją ułamka łańcuchowego liczby niewymiernej  x , wtedy

${\ Displaystyle \ Operatorname {?} (x) = a_ {0}+2 \ suma _ {n = 1} ^ {\ infty} {\ Frac {\ lewo (-1 \ po prawej) ^ {n + 1}} {2^{a_{1}+\cdots +a_{n}}},}$

mając na uwadze, że jeśli [ a ₀ ; a ₁ , a ₂ , …, a _m ] jest reprezentacją ułamka łańcuchowego liczby wymiernej  x , wtedy

${\ Displaystyle \ Operatorname {?} (x) = a_ {0}+2 \ suma _ {n = 1} ^ {m} {\ Frac {\ po lewej (-1 \ po prawej) ^ {n + 1}} { 2^{a_{1}+\cdots +a_{n}}}}.}$

Intuicyjne wyjaśnienie

Aby uzyskać intuicję dotyczącą powyższej definicji, rozważ różne sposoby interpretacji nieskończonego ciągu bitów zaczynającego się od 0 jako liczby rzeczywistej w [0, 1] . Jednym z oczywistych sposobów interpretacji takiego ciągu jest umieszczenie kropki binarnej po pierwszym 0 i odczytanie ciągu jako rozwinięcia binarnego : na przykład ciąg 001001001001001001001001... reprezentuje liczbę binarną 0.010010010010... lub2/7. Inna interpretacja postrzega ciąg znaków jako ułamek ciągły [0; a ₁ ,  a ₂ , …] , gdzie liczby całkowite a _i są długościami ciągów w kodowaniu ciągów znaków. Ten sam przykładowy ciąg 001001001001001001001001... odpowiada następnie [0; 2, 1, 2, 1, 2, 1, …] =√ 3 − 1/2. Jeśli ciąg kończy się nieskończenie długim ciągiem tego samego bitu, ignorujemy go i kończymy reprezentację; sugeruje to formalna „tożsamość”:

[0; a ₁ , …, a _n , ∞] = [0; a ₁ , …, a _n +1/∞] = [0; a ₁ , …, a _n + 0] = [0; ₁ , ..., _n ] .

Wpływ funkcji znaku zapytania na [0, 1] można zatem rozumieć jako odwzorowanie drugiej interpretacji ciągu na pierwszą interpretację tego samego ciągu, tak jak funkcję Cantora można rozumieć jako odwzorowanie triadycznej bazy 3 reprezentacja na reprezentację o podstawie 2. Nasz przykładowy ciąg daje równość

${\ Displaystyle \ operatorname {?} \ lewo ({\ Frac {{\ sqrt {3}}-1} {2}} \ prawej) = {\ Frac {2} {7}}.}$

Rekurencyjna definicja argumentów racjonalnych

Dla liczb wymiernych w przedziale jednostkowym funkcja może być również zdefiniowana rekurencyjnie ; JeśliP/Q oraz r/ssą ułamkami zredukowanymi takimi, że | ps − rq | = 1 (tak, że są one sąsiadującymi elementami rzędu ciągu Fareya ) then

${\ Displaystyle \ operatorname {?} \ lewo ({\ Frac {p + R} {q + s}} \ prawo) = {\ Frac {1} {2}} \ lewo [\ operator {?} \ lewo ( {\frac {p}{q}}\right)+\nazwa operatora {?} \left({\frac {r}{s}}\right)\right].}$

Korzystanie z podstawowych przypadków

${\ Displaystyle \ operatorname {?} \ lewo ({\ Frac {0}{1}} \ prawo) = 0 \ quad {\ tekst {i}} \ quad \ operatorname {?} \ lewo ({\ Frac {1 }{1}}\prawo)=1,}$

wtedy można obliczyć ?( x ) dla dowolnego wymiernego  x , zaczynając od sekwencji Fareya rzędu 2, potem 3 itd.

Gdyby p _{n- 1}/q _{n −1} oraz p _n/q _nto dwie kolejne zbieżności ułamka łańcuchowego , to macierz

${\ Displaystyle {\ zacząć {pmatrix} p_ {n-1} i p_ {n} \ \ q_ {n-1} i q_ {n} \ koniec {pmatrix}}}$

ma wyznacznik  ±1. Taka macierz jest elementem SL(2,  Z ) , grupy macierzy 2 × 2 z wyznacznikiem ±1. Ta grupa jest powiązana z grupą modułową .

Samosymetria

Znak zapytania jest wyraźnie podobny wizualnie. Monoid samodzielnych podobieństwa mogą być generowane przez dwóch operatorów S i R działających na placu jednostkę i określa się następująco:

${\ Displaystyle {\ zacząć {wyrównany} S (x, y) i = \ lewo ({\ Frac {x} {x + 1}}, {\ Frac {y} {2}} \ prawej), \ \ [ 5px]R(x,y)&=(1-x,1-y).\end{wyrównany}}}$

Wizualnie S zmniejsza kwadrat jednostki do jego lewej dolnej ćwiartki, podczas gdy R wykonuje odbicie punktowe przez jego środek.

Punkt na wykresie z ? ma współrzędne ( x , ?( x )) dla pewnego x w przedziale jednostkowym. Taki punkt jest przekształcany przez S i R w inny punkt wykresu, ponieważ ? spełnia następujące tożsamości dla wszystkich x ∈ [0, 1] :

${\ Displaystyle {\ zacząć {wyrównany} \ nazwa operatora {?} \ lewo ({\ Frac {x} {x + 1}} \ prawej) i = {\ Frac {\ nazwa operatora {?} (x)} {2} },\\[5px]\nazwa operatora {?} (1-x)&=1-\nazwa operatora {?} (x).\end{wyrównany}}}$

Te dwa operatory mogą być wielokrotnie łączone, tworząc monoid. Ogólnym elementem monoidu jest zatem

${\ Displaystyle S ^ {a_ {1}} RS ^ {a_ {2}} RS ^ {a_ {3}} \ cdots}$

dla liczb całkowitych dodatnich a ₁ , a ₂ , a ₃ , … . Każdy taki element opisuje samopodobieństwo funkcji znaku zapytania. Monoid ten jest czasem nazywany monoidem podwajania okresów , a wszystkie krzywe fraktalne podwajania okresów mają opisaną przez siebie samosymetrię ( kategorią takich krzywych jest krzywa de Rhama , której znak zapytania jest przypadkiem szczególnym). Elementy monoid są odpowiednio z wymiernych poprzez identyfikację w ₁ , ₂ , ₃ ... z ułamka [0; a ₁ , a ₂ , a ₃ ,…] . Od kiedy oboje

${\ Displaystyle S: x \ mapsto {\ Frac {x} {x + 1}}}$

oraz

${\displaystyle T:x\mapsto 1-x}$

są liniowymi przekształceniami ułamkowymi o współczynnikach całkowitych, monoid może być traktowany jako podzbiór grupy modułowej PSL(2, Z ) .

irracjonalne kwadratowe

Funkcja znaku zapytania zapewnia odwzorowanie jeden-do-jednego z niewymiernych wymiernych na kwadratowe wymierne , co pozwala na jednoznaczny dowód policzalności tych ostatnich. Mogą one, w rzeczywistości należy rozumieć odpowiadają okresowych orbity dla diadycznej transformacji . Można to wyraźnie zademonstrować w zaledwie kilku krokach.

Symetria diadyczna

Zdefiniuj dwa ruchy: ruch w lewo i ruch w prawo, ważne w interwale jednostkowym jako ${\displaystyle 0\leq x\leq 1}$

${\ Displaystyle L_ {D} (x) = {\ Frac {x} {2}}}$ oraz ${\ Displaystyle L_ {C} (x) = {\ Frac {x} {1 + x}}}$

oraz

${\ Displaystyle R_ {D} (x) = {\ Frac {1 + x} {2}}}$ oraz ${\ Displaystyle R_ {C} (x) = {\ Frac {1} {2-x}}}$

Funkcja znaku zapytania zachowuje wtedy symetrię ruchu w lewo

${\ Displaystyle L_ {D} \ circ ? =? \ circ L_ {C}}$

i symetria ruchu w prawo

${\ Displaystyle R_ {D} \ circ ? =? \ circ R_ {C}}$

gdzie oznacza kompozycję funkcji . Mogą być dowolnie łączone. Rozważmy na przykład sekwencję ruchów lewo-prawo Dodanie indeksów dolnych C i D oraz, dla jasności, porzucenie operatora kompozycji we wszystkich miejscach poza kilkoma, mamy: ${\displaystyle \circ}$${\ Displaystyle LRLLR.}$${\displaystyle \circ}$

${\ Displaystyle L_ {D} R_ {D} L_ {D} L_ {D} R_ {D} \ circ ? =? \ circ L_ {C} R_ {C} L_ {C} L_ {C} R_ {C} }$

Arbitralne łańcuchy o skończonej długości w literach L i R odpowiadają wymiernym diadycznym , w tym sensie , że każdy wymierny dwudniowy można zapisać zarówno jako liczby całkowite n i m, jak i jako skończoną długość bitów z Tak więc każda wymierność dwudniowa jest w jednym do- jedna korespondencja z pewną samosymetrią funkcji znaku zapytania. ${\ Displaystyle y = n/2 ^ {m}}$${\displaystyle y=0.b_{1}b_{2}b_{3}\cdots b_{m}}$${\ Displaystyle b_ {k} \ w \ {0,1 \}.}$

Niektóre zmiany notacji mogą nieco ułatwić wyrażenie powyższego. Niech i oznaczają L i R. Złożenie funkcji rozszerza to na monoid , w którym można pisać i ogólnie dla niektórych binarnych ciągów cyfr A , B , gdzie AB jest zwykłym połączeniem takich ciągów. Monoid diady M jest zatem monoidem wszystkich takich ruchów lewo-prawo o skończonej długości. Pisząc jako ogólny element monoidu, odpowiada mu samosymetria funkcji znaku zapytania: ${\displaystyle g_{0}}$${\displaystyle g_{1}}$${\displaystyle g_010}=g_{0}g_{1}g_{0}}$${\ Displaystyle g_ {A} g_ {B} = g_ {AB}}$${\ Displaystyle \ gamma \ w M}$

${\ Displaystyle \ gamma _ {D} \ circ ? =? \ circ \ gamma _ {C}}$

Izomorfizm

Wyraźne odwzorowanie między wymiernymi a dwuczłonowymi wymiernymi można uzyskać, zapewniając operator odbicia

${\ Displaystyle r (x) = 1-x}$

i zauważając, że obaj

${\ Displaystyle r \ circ R_ {D} \ circ r = L_ {D}}$ oraz ${\ Displaystyle r \ circ R_ {C} \ circ r = L_ {C}}$

Ponieważ jest tożsamość, arbitralne ciąg lewo-prawo ruchów można ponownie zapisać jako ciąg tylko przemieszcza się w lewo, a następnie odbicie, a następnie bardziej lewicowych ruchów, refleksji, i tak dalej, to jest, jak co jest wyraźnie izomorficzny do góry. Obliczenie pewnej wyraźnej sekwencji na argumencie funkcji daje racjonalny dwudniowy; wyraźnie jest równa, gdzie każdy jest bitem binarnym, zero odpowiada ruchowi w lewo, a jeden odpowiada ruchowi w prawo. Równoważna sekwencja ruchów, oceniona jako, daje liczbę wymierną. Jest to wyraźnie ta, którą dostarcza ułamek łańcuchowy, pamiętając, że jest ona wymierna, ponieważ ciąg ma skończoną długość. To ustanawia relację jeden-do-jednego między racjonałami diadycznymi a rozumnymi. ${\ Displaystyle r ^ {2} = 1}$${\ Displaystyle L ^ {a_ {1}} rL ^ {a_ {2}} rL ^ {a_ {3}} \ cdots}$${\ Displaystyle S ^ {a_ {1}} TS ^ {a_ {2}} TS ^ {a_ {3}} \ cdots}$${\ Displaystyle L_ {D}, R_ {D}}$${\displaystyle x=1}$${\displaystyle y=0.b_{1}b_{2}b_{3}\cdots b_{m}}$${\ Displaystyle b_ {k} \ w \ {0,1 \}}$${\ Displaystyle L_ {C}, R_ {C}}$${\displaystyle x=1}$${\displaystyle p/q.}$${\displaystyle p/q=[a_{1},a_{2},a_{3},\cdots,a_{j}]}$${\displaystyle (a_{1},a_{2},a_{3},\cdots,a_{j})}$

Okresowe orbity transformaty dwójkowej

Rozważmy teraz okresowe orbity na diadycznej transformacji . Odpowiadają one sekwencjom bitowym składającym się ze skończonej początkowej „chaotycznej” sekwencji bitów , po której następuje powtarzający się ciąg o długości . Takie powtarzające się ciągi odpowiadają liczbie wymiernej. Łatwo to wyjaśnić. Pisać ${\displaystyle b_{0},b_{1},b_{2},\cdots,b_{k-1}}$${\ Displaystyle b_ {k}, b_ {k + 1}, b_ {k + 2}, \ cdots, b_ {k + m-1}}$${\ Displaystyle m}$

${\ Displaystyle y = \ suma _ {j = 0} ^ {m-1} b_ {k + j} 2 ^ {-j-1}}$

jeden to wyraźnie ma

${\ Displaystyle \ suma _ {j = 0} ^ {\ infty} b_ {k + j} 2 ^ {-j-1} = y \ suma _ {j = 0} ^ {\ infty} 2 ^ {-jm }={\frac {y}{1-2^{m}}}}$

Włączając początkową nie powtarzającą się sekwencję, mamy wyraźnie liczbę wymierną. W rzeczywistości każdą liczbę wymierną można wyrazić w ten sposób: początkowa „losowa” sekwencja, po której następuje cykliczne powtórzenie. Oznacza to, że okresowe orbity mapy odpowiadają jeden do jednego z wymiernymi.

Orbity okresowe jako ułamki ciągłe

Takie orbity okresowe mają równoważny ułamek okresowy ciągły, zgodnie z izomorfizmem ustalonym powyżej. Istnieje początkowa „chaotyczna” orbita o pewnej skończonej długości, po której następuje powtarzająca się sekwencja. Powtarzająca się sekwencja generuje okresowy ułamek ciągły spełniający Ten ułamek ciągły ma postać ${\ Displaystyle x = [a_ {n}, a_ {n + 1}, a_ {n + 2}, \ cdots, a_ {n + r}, x].}$

${\displaystyle x={\frac {\alfa x+\beta}{\gamma x+\delta}}}$

z byciem liczbami całkowitymi, a satysfakcjonujące wartości Jawne można uzyskać, pisząc ${\displaystyle \alfa,\beta,\gamma,\delta}$${\ Displaystyle \ alfa \ delta - \ beta \ gamma = \ pm 1.}$

${\ Displaystyle S \ mapsto {\ zacząć {pmatrix} 1 i 0 \ \ 1 i 1 \ koniec {pmatrix}}}$

na zmianę, żeby

${\ Displaystyle S ^ {n} \ mapsto {\ zacząć {pmatrix} 1 i 0 \ \ n i 1 \ koniec {pmatrix}}}$

podczas gdy odbicie jest podane przez

${\ Displaystyle T \ mapsto {\ zacząć {pmatrix} -1 i 1 \ \ 0 i 1 \ koniec {pmatrix}}}$

tak, że . Obie te macierze są unimodularne , dowolne iloczyny pozostają unimodularne i dają macierz postaci ${\ Displaystyle T ^ {2} = ja}$

${\ Displaystyle S ^ {a_ {n}} TS ^ {a_ {n + 1}} T \ cdots TS ^ {a_ {n + r}} = {\ zacząć {pmatrix} \ alfa i \ beta \ \ \ gamma &\delta \end{pmatrix}}}$

podając dokładną wartość ułamka łańcuchowego. Ponieważ wszystkie wpisy macierzy są liczbami całkowitymi, ta macierz należy do projekcyjnej grupy modułowej ${\ Displaystyle PSL (2, \ mathbb {Z}).}$

Rozwiązując jawnie, mamy to. Nietrudno zweryfikować, czy rozwiązania tego problemu spełniają definicję niewymiernych kwadratów. W rzeczywistości w ten sposób można wyrazić każdą kwadratową irracjonalność. Zatem kwadratowe irracjonalne są w relacji jeden-do-jednego z okresowymi orbitami transformacji dwuczłonowej, które są w relacji jeden-do-jednego z (niediadycznymi) wymiernymi, które są w relacji jeden-do-jednego z rozumowania dwudniowe. Funkcja znaku zapytania zapewnia korespondencję w każdym przypadku. ${\ Displaystyle \ gamma x ^ {2} + (\ delta - \ alfa) x- \ beta = 0.}$

Właściwości ?( x )

Funkcja znaku zapytania jest funkcją ściśle rosnącą i ciągłą, ale nie absolutnie ciągłą . Pochodna jest określona prawie wszędzie i może przyjmować tylko dwie wartości 0 (wartość prawie wszędzie, w tym na wszystkich liczb wymiernych ) oraz . Istnieje kilka konstrukcji miary, która po zintegrowaniu daje funkcję znaku zapytania. Jedną z takich konstrukcji uzyskuje się mierząc gęstość liczb Fareya na osi liczb rzeczywistych. Miara ze znakiem zapytania jest prototypowym przykładem tego, co czasami określa się mianem miar multifraktalnych . ${\displaystyle +\infty}$

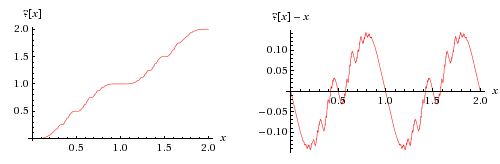
Funkcja znaku zapytania odwzorowuje liczby wymierne na dwójkowe liczby wymierne , czyli te, których podstawowa reprezentacja kończy się, jak można dowieść przez indukcję z konstrukcji rekurencyjnej opisanej powyżej. Odwzorowuje to kwadratowe Irrationals do non-dwójkowym liczb wymiernych. W obu przypadkach zapewnia to izomorfizm rzędów między tymi zbiorami, czyniąc konkretne twierdzenie o izomorfizmie Cantora, zgodnie z którym każde dwa nieograniczone, policzalne gęste rzędy liniowe są izomorficzne w rzędzie. Jest to funkcja nieparzysta i spełnia równanie funkcjonalne ?( x + 1) = ?( x ) + 1 ; w konsekwencji x → ?( x ) − x jest nieparzystą funkcją okresową z pierwszym okresem. Jeśli ?( x ) jest niewymierne, to x jest albo algebraiczne o stopniu większym niż dwa, albo transcendentalne .

Funkcja znaku zapytania ma stałe punkty na 0,1/2i 1 i co najmniej dwa inne, symetryczne wokół punktu środkowego. Jeden to około 0,42037. Moshchevitin przypuszczał, że są to jedyne 5 stałych punktów.

W 1943 Raphaël Salem postawił pytanie, czy współczynniki Fouriera-Stieltjesa funkcji znaku zapytania znikają w nieskończoności. Innymi słowy, chciał wiedzieć, czy…

${\ Displaystyle \ lim _ {n \ do \ infty} \ int _ {0} ^ {1} e ^ {2 \ pi inx} \ \ operatorname {d?} (x) = 0.}$

Na to odpowiedzieli twierdząco Jordan i Sahlsten, jako szczególny przypadek wyniku środków Gibbsa .

Wykres funkcji znaku zapytania Minkowskiego jest szczególnym przypadkiem krzywych fraktalnych zwanych krzywymi de Rama .

Algorytm

Definicja rekurencyjna naturalnie nadaje się do algorytmu obliczania funkcji z dowolnym pożądanym stopniem dokładności dla dowolnej liczby rzeczywistej, jak pokazuje następująca funkcja C. Algorytm schodzi w dół drzewa Sterna-Brocota w poszukiwaniu danych wejściowych  x i po drodze sumuje warunki rozwinięcia binarnego y = ?( x ) . Dopóki niezmiennik pętli qr − ps = 1 pozostaje spełniony, nie ma potrzeby zmniejszania ułamkam/n = p + r/q + s, ponieważ jest już na najniższym poziomie. Innym niezmiennikiem jestP/Q≤ x <r/s. forPętla w tym programie mogą być analizowane trochę jak whilepętla, z warunkowym sprawozdania przerwa w pierwszych trzech wierszy składających się warunku. Jedyne instrukcje w pętli, które mogą mieć wpływ na niezmienniki, znajdują się w ostatnich dwóch wierszach i można wykazać, że zachowują one prawdziwość obu niezmienników, o ile pierwsze trzy wiersze zostały wykonane pomyślnie bez przerwania pętli. Trzeci niezmiennik dla ciała pętli (do dokładności zmiennoprzecinkowej) to y ≤ ?( x ) < y + d , ale ponieważ d jest zmniejszane o połowę na początku pętli przed sprawdzeniem jakichkolwiek warunków, nasz wniosek jest taki, że y ≤ ?( x ) < y + 2 d na końcu pętli.

Aby udowodnić zakończenie , wystarczy zauważyć, że suma q + szwiększa się o co najmniej 1 z każdą iteracją pętli i że pętla kończy się, gdy ta suma jest zbyt duża, aby można ją było przedstawić w prymitywnym typie danych C long. Jednak w praktyce warunkowe przerwanie kiedy y + d == yzapewnia zakończenie pętli w rozsądnym czasie.

/* Minkowski's question-mark function */
double minkowski(double x) {
    long p = x;
    if ((double)p > x) --p; /* p=floor(x) */
    long q = 1, r = p + 1, s = 1, m, n;
    double d = 1, y = p;
    if (x < (double)p || (p < 0) ^ (r <= 0))
        return x; /* out of range ?(x) =~ x */
    for (;;) { /* invariants: q * r - p * s == 1 && (double)p / q <= x && x < (double)r / s */
        d /= 2;
        if (y + d == y)
            break; /* reached max possible precision */
        m = p + r;
        if ((m < 0) ^ (p < 0))
            break; /* sum overflowed */
        n = q + s;
        if (n < 0)
            break; /* sum overflowed */

        if (x < (double)m / n) {
            r = m;
            s = n;
        } else {
            y += d;
            p = m;
            q = n;
        }
    }
    return y + d; /* final round-off */
}

Rozkład prawdopodobieństwa

Ograniczanie Minkowski znak zapytania funkcję do: [0,1] → [0,1], może być używany jako skumulowanej funkcji rozkładu z pojedynczej dystrybucji na przedział jednostkowy. Rozkład ten jest symetryczny względem jego punktu środkowego, z surowymi momentami około m ₁  = 0,5, m ₂  = 0,290926, m ₃  = 0,186389 i m ₄  = 0,126992, a więc średnia i mediana 0,5, odchylenie standardowe około 0,2023, a skośność 0, a kurtoza nadmierna około -1,147.

Funkcja skrzynki Conway

Ponieważ funkcja znaku zapytania Minkowskiego jest ściśle rosnącą, ciągłą bijekcją z liczb rzeczywistych na liczby rzeczywiste, ma ona funkcję odwrotną zwaną funkcją Conway box . Więc ... ${\ Displaystyle \ kwadrat (? (x)) = x {\ tekst {i}}? (\ kwadrat (y)) = y}$

To odwzorowuje wymierności dwuczłonowe na wymierne, a wymierne na pole kwadratowe. Argument kardynalności pokazuje, że bez względu na to, ile razy zostanie to powtórzone, prawie wszystkie liczby rzeczywiste są w tym sensie nie do pakowania .

Zobacz też

• Pochodna Pompejusza

Uwagi

odniesienia historyczne

• Minkowski, Hermann (1904), "Zur Geometrie der Zahlen", Verhandlungen des III. Internationalen Mathematiker-Kongresses w Heidelbergu , Berlinie, s. 164-173, JFM  36.0281.01 , archiwizowane z oryginałem w dniu 4 stycznia 2015
• Denjoy, Arnaud (1938), „Sur une fonction réelle de Minkowski”, J. Math. Pures Appl. , Série IX (po francusku), 17 : 105–151, Zbl  0018.34602

Bibliografia

• Alkauskas, Giedrius (2008), Przekształcenia całkowe funkcji znaku zapytania Minkowskiego , praca doktorska, University of Nottingham.
• Bibiloni, L.; Paradis, J.; Viader, P. (1998), "Nowe światło na funkcję Minkowskiego ?(x)" , Journal of Number Theory , 73 (2): 212–227, doi : 10.1006/jnth.1998.2294 , hdl : 10230/843 , Zbl  0928.11006 , zarchiwizowane od oryginału z dnia 22 czerwca 2015 r..
• Bibiloni, L.; Paradis, J.; Viader, P. (2001), "Pochodna funkcji pojedynczej Minkowskiego" , Journal of Mathematical Analysis and Applications , 253 (1): 107-125, doi : 10,1006 / jmaa.2000.7064 , Zbl  +0.995,26005 , archiwizowane z oryginałem w dniu 22 Czerwiec 2015.
• Conley, RM (2003), Ankieta funkcji Minkowskiego ?(x) , praca magisterska, West Virginia University.
• Conway, JH (2000), "wykrzywione frakcje", O liczbach i grach (2nd ed.), Wellesley, MA: AK Peters, s. 82-86.
• Finch, Steven R. (2003), Stałe matematyczne , Encyklopedia Matematyki i jej Zastosowania, 94 , Cambridge : Cambridge University Press , ISBN 978-0-521-81805-6, Zbl  1054.00001
• Jordan, Tomasz; Sahlsten, Tuomas (2016), "Transformacje Fouriera miar Gibbsa dla mapy Gaussa", Mathematische Annalen , 364 (3-4): 983-1023, arXiv : 1312.3619 , Bibcode : 2013arXiv1312.3619J , doi : 10.1007/s00208-015 -1241-9
• Pyteas Fogg, N. (2002), Berthé, Valérie ; Ferenczi, Sebastien; Mauduit, chrześcijanin; Siegel, A. (red.), Substitutions in dynamics, aithmetics and combinatorics , Lecture Notes in Mathematics, 1794 , Berlin: Springer-Verlag , ISBN 978-3-540-44141-0, Zbl  1014.11015
• Salem, Raphaël (1943), „O niektórych pojedynczych monotonicznych funkcjach, które ściśle rosną” (PDF) , Transactions of the American Mathematical Society , 53 (3): 427-439, doi : 10.2307/1990210 , JSTOR  1990210
• Vepstas, L. (2004), Znak zapytania Minkowskiego i grupa modułowa SL(2,Z) (PDF)
• Vepstas, L. (2008), "Na miarce Minkowskiego", arXiv : 0810.1265 [ math.DS ]

Zewnętrzne linki

• Obszerna lista bibliograficzna
• Weisstein, Eric W. "Funkcja znaku zapytania Minkowskiego" . MatematykaŚwiat .
• Prosta implementacja IEEE 754 w C++