Niecentralny rozkład t - Noncentral t-distribution

Niecentralny t Studenta

Funkcja gęstości prawdopodobieństwa
Parametry	ν> 0 stopni swobody parametr niecentralności ${\ Displaystyle \ mu \ in \ Re \, \!}$
Wsparcie	${\ Displaystyle x \ in (- \ infty; + \ infty) \ \!}$
PDF	zobacz tekst
CDF	zobacz tekst
Oznaczać	zobacz tekst
Tryb	zobacz tekst
Zmienność	zobacz tekst
Skośność	zobacz tekst
Dawny. kurtoza	zobacz tekst

Noncentral t -Dystrybucja uogólnia Studenta t -Dystrybucja użyciu parametru noncentrality . Podczas gdy centralny rozkład prawdopodobieństwa opisuje, jak rozkłada się statystyka testowa t, gdy testowana różnica jest zerowa, rozkład niecentralny opisuje rozkład t, gdy wartość zerowa jest fałszywa. Prowadzi to do wykorzystania go w statystykach, zwłaszcza do obliczania mocy statystycznej . Noncentral t -Dystrybucja znany jest również jako pojedynczo noncentral t -Dystrybucja, a ponadto do jego pierwotnej stosowania wnioskowania statystycznego , stosuje się również w wytrzymałej modelowania dla danych .

Charakteryzacja

Jeśli Z jest zmienną losową o rozkładzie normalnym z jednostkową wariancją i zerową średnią, a V jest zmienną losową o rozkładzie chi-kwadrat z ν stopniami swobody, która jest niezależna od Z , to

${\ Displaystyle T = {\ Frac {Z + \ mu} {\ sqrt {V / \ nu}}}}$

jest niecentralną zmienną losową o rozkładzie t z ν stopniami swobody i parametrem niecentralności μ ≠ 0. Należy zauważyć, że parametr niecentralności może być ujemny.

Dystrybuanta

Skumulowanego rozkład z noncentral t -Dystrybucja z ν stopnie swobody i noncentrality parametr μ można wyrazić

${\ Displaystyle F _ {\ nu, \ mu} (x) = {\ rozpocząć {przypadków} {\ tilde {F}} _ {\ nu, \ mu} (x) i {\ mbox {if}} x \ geq 0; \\ 1 - {\ tilde {F}} _ {\ nu, - \ mu} (x), & {\ mbox {if}} x <0, \ end {cases}}}$

gdzie

${\ Displaystyle {\ tilde {F}} _ {\ nu, \ mu} (x) = \ Phi (- \ mu) + {\ Frac {1} {2}} \ suma _ {j = 0} ^ { \ infty} \ left [p_ {j} I_ {y} \ left (j + {\ frac {1} {2}}, {\ frac {\ nu} {2}} \ right) + q_ {j} I_ { y} \ left (j + 1, {\ frac {\ nu} {2}} \ right) \ right],}$

${\ Displaystyle I_ {y} \ \! (a, b)}$ jest uregulowaną niekompletną funkcją beta ,

${\ Displaystyle y = {\ Frac {x ^ {2}} {x ^ {2} + \ nu}},}$

${\ Displaystyle p_ {j} = {\ Frac {1} {j!}} \ exp \ lewo \ {- {\ Frac {\ mu ^ {2}} {2}} \ prawo \} \ lewo ({\ frac {\ mu ^ {2}} {2}} \ right) ^ {j},}$

${\ Displaystyle q_ {j} = {\ Frac {\ mu} {{\ sqrt {2}} \ Gamma (j + 3/2)}} \ exp \ lewo \ {- {\ Frac {\ mu ^ {2 }} {2}} \ right \} \ left ({\ frac {\ mu ^ {2}} {2}} \ right) ^ {j},}$

a Φ jest skumulowaną funkcją rozkładu standardowego rozkładu normalnego .

Alternatywnie, niecentralny CDF z rozkładem t można wyrazić jako:

${\ Displaystyle F_ {v, \ mu} (x) = {\ rozpocząć {przypadków} {\ Frac {1} {2}} \ sum _ {j = 0} ^ {\ infty} {\ Frac {1} { j!}} (- \ mu {\ sqrt {2}}) ^ {j} e ^ {\ frac {- \ mu ^ {2}} {2}} {\ frac {\ Gamma ({\ frac {j +1} {2}})} {\ sqrt {\ pi}}} I \ left ({\ frac {v} {v + x ^ {2}}}; {\ frac {v} {2}}, {\ frac {j + 1} {2}} \ right), & x \ geq 0 \\ 1 - {\ frac {1} {2}} \ sum _ {j = 0} ^ {\ infty} {\ frac {1} {j!}} (- \ mu {\ sqrt {2}}) ^ {j} e ^ {\ frac {- \ mu ^ {2}} {2}} {\ frac {\ Gamma ({ \ frac {j + 1} {2}})} {\ sqrt {\ pi}}} I \ left ({\ frac {v} {v + x ^ {2}}}; {\ frac {v} { 2}}, {\ frac {j + 1} {2}} \ right), & x <0 \ end {cases}}}$

gdzie Γ jest funkcją gamma, a ja jest uregulowaną niekompletną funkcją beta .

Chociaż istnieją inne formy skumulowanej funkcji dystrybucji, pierwsza z przedstawionych powyżej postaci jest bardzo łatwa do oszacowania za pomocą obliczeń rekurencyjnych . W oprogramowaniu statystycznym R skumulowana funkcja dystrybucji jest zaimplementowana jako pkt .

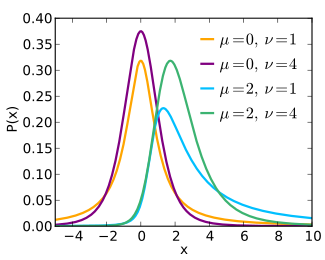
Funkcja gęstości prawdopodobieństwa

Funkcja gęstości prawdopodobieństwa (pdf) dla niecentralnego rozkładu t z ν> 0 stopni swobody i parametrem niecentralności μ można wyrazić w kilku formach.

Konfluentne hipergeometryczny funkcja postać funkcji gęstości jest

${\ displaystyle f (x) = \ underbrace {{\ Frac {\ Gamma ({\ Frac {\ nu +1} {2}})} {{\ sqrt {\ nu \ pi}} \ Gamma ({\ Frac {\ nu} {2}})}} \ left (1 + {\ frac {x ^ {2}} {\ nu}} \ right) ^ {- {\ tfrac {\ nu +1} {2}} }} _ {{\ text {StudentT}} (x \,; \, \ mu = 0)} \ exp {\ big (} - {\ tfrac {\ mu ^ {2}} {2}} {\ big )} {\ Big \ {} A _ {\ nu} (x \,; \, \ mu) + B _ {\ nu} (x \,; \, \ mu) {\ Big \}},}$

gdzie

${\ Displaystyle {\ rozpocząć {wyrównane} A _ {\ nu} (x \,; \, \ mu) & = {_ {1} F} _ {1} \ lewo ({\ Frac {\ nu +1} { 2}} \,; \, {\ frac {1} {2}} \,; \, {\ frac {\ mu ^ {2} x ^ {2}} {2 (x ^ {2} + \ nu )}} \ right), \\ B _ {\ nu} (x \,; \, \ mu) & = {\ frac {{\ sqrt {2}} \ mu x} {\ sqrt {x ^ {2} + \ nu}}} {\ frac {\ Gamma ({\ frac {\ nu} {2}} + 1)} {\ Gamma ({\ frac {\ nu +1} {2}})}} {_ {1} F} _ {1} \ left ({\ frac {\ nu} {2}} + 1 \,; \, {\ frac {3} {2}} \,; \, {\ frac {\ mu ^ {2} x ^ {2}} {2 (x ^ {2} + \ nu)}} \ right), \ end {aligned}}}$

i gdzie ₁ F ₁ jest konfluentną funkcją hipergeometryczną .

Alternatywną formą całkową jest

${\ Displaystyle f (x) = {\ Frac {\ nu ^ {\ Frac {\ nu} {2}} \ exp \ left (- {\ Frac {\ nu \ mu ^ {2}} {2 (x ^ {2} + \ nu)}} \ right)} {{\ sqrt {\ pi}} \ Gamma ({\ frac {\ nu} {2}}) 2 ^ {\ frac {\ nu -1} {2 }} (x ^ {2} + \ nu) ^ {\ frac {\ nu +1} {2}}}} \ int _ {0} ^ {\ infty} y ^ {\ nu} \ exp \ left ( - {\ frac {1} {2}} \ left (y - {\ frac {\ mu x} {\ sqrt {x ^ {2} + \ nu}}} \ right) ^ {2} \ right) dy .}$

Trzecią postać gęstości uzyskuje się za pomocą jej dystrybucyjnych funkcji w następujący sposób.

${\ Displaystyle f (x) = {\ rozpocząć {przypadków} {\ Frac {\ nu} {x}} \ lewo \ {F _ {\ nu +2, \ mu} \ lewo (x {\ sqrt {1+ { \ frac {2} {\ nu}}} \ right) -F _ {\ nu, \ mu} (x) \ right \}, & {\ mbox {if}} x \ neq 0; \\ {\ frac {\ Gamma ({\ frac {\ nu +1} {2}})} {{\ sqrt {\ pi \ nu}} \ Gamma ({\ frac {\ nu} {2}})}} \ exp \ left (- {\ frac {\ mu ^ {2}} {2}} \ right), & {\ mbox {if}} x = 0. \ end {cases}}}$

Podejście to zostało wprowadzone przez dt funkcji w R .

Nieruchomości

Momenty noncentral t -Dystrybucja

Ogólnie rzecz biorąc, k- ty surowy moment niecentralnego rozkładu t to

${\ Displaystyle {\ mbox {E}} \ lewo [T ^ {k} \ prawej] = {\ rozpocząć {przypadków} \ lewo ({\ Frac {\ nu} {2}} \ prawo) ^ {\ Frac { k} {2}} {\ frac {\ Gamma \ left ({\ frac {\ nu -k} {2}} \ right)} {\ Gamma \ left ({\ frac {\ nu} {2}} \ right)}} {\ mbox {exp}} \ left (- {\ frac {\ mu ^ {2}} {2}} \ right) {\ frac {d ^ {k}} {d \ mu ^ {k }}} {\ mbox {exp}} \ left ({\ frac {\ mu ^ {2}} {2}} \ right), & {\ mbox {if}} \ nu> k; \\ {\ mbox {Nie istnieje}}, & {\ mbox {if}} \ nu \ leq k. \\\ end {cases}}}$

W szczególności średnia i wariancja niecentralnego rozkładu t są

${\ Displaystyle {\ rozpocząć {wyrównane} {\ mbox {E}} \ lewo [T \ prawo] & = {\ rozpocząć {przypadków} \ mu {\ sqrt {\ frac {\ nu} {2}}} {\ frac {\ Gamma ((\ nu -1) / 2)} {\ Gamma (\ nu / 2)}}, & {\ mbox {if}} \ nu> 1; \\ {\ mbox {Nie istnieje} }, & {\ mbox {if}} \ nu \ leq 1, \\\ end {cases}} \\ {\ mbox {Var}} \ left [T \ right] & = {\ begin {cases} {\ frac {\ nu (1+ \ mu ^ {2})} {\ nu -2}} - {\ frac {\ mu ^ {2} \ nu} {2}} \ left ({\ frac {\ Gamma ( (\ nu -1) / 2)} {\ Gamma (\ nu / 2)}} \ right) ^ {2}, & {\ mbox {if}} \ nu> 2; \\ {\ mbox {Nie istnieje}}, & {\ mbox {if}} \ nu \ leq 2. \\\ end {cases}} \ end {aligned}}}$

Doskonałe przybliżenie to , które można zastosować w obu formułach. ${\ Displaystyle {\ sqrt {\ Frac {\ nu} {2}}} {\ Frac {\ Gamma ((\ nu -1) / 2)} {\ Gamma (\ nu / 2)}}}$${\ Displaystyle \ lewo (1 - {\ Frac {3} {4 \ nu -1}} \ prawej) ^ {- 1}}$

Asymetria

Non-centralnej t -Dystrybucja jest asymetryczny, chyba μ wynosi zero, czyli centralny t -Dystrybucja. Ponadto asymetria maleje wraz z większym stopniem swobody. Prawy ogon będzie cięższy niż lewy, gdy μ> 0 i odwrotnie. Jednak zwykła skośność nie jest ogólnie dobrą miarą asymetrii dla tego rozkładu, ponieważ jeśli stopnie swobody nie są większe niż 3, trzeci moment w ogóle nie istnieje. Nawet jeśli stopnie swobody są większe niż 3, próbna ocena skośności jest nadal bardzo niestabilna, chyba że wielkość próbki jest bardzo duża.

Tryb

Niecentralny rozkład t jest zawsze unimodalny i ma kształt dzwonu, ale mod nie jest dostępny analitycznie, chociaż dla μ ≠ 0 mamy

${\ Displaystyle {\ sqrt {\ Frac {\ nu} {\ nu + (5/2)}}} <{\ Frac {\ mathrm {tryb}} {\ mu}} <{\ sqrt {\ frac {\ nu} {\ nu +1}}}}$

W szczególności tryb ma zawsze ten sam znak, co parametr niecentralności μ. Co więcej, ujemna postać modu jest dokładnie tym trybem dla niecentralnego rozkładu t- Studenta z taką samą liczbą stopni swobody ν, ale z parametrem niecentralności −μ.

Tryb rośnie ściśle z μ (zawsze porusza się w tym samym kierunku, w jakim μ jest ustawiane). W granicy, gdy μ → 0, tryb jest aproksymowany przez

${\ Displaystyle {\ sqrt {\ Frac {\ nu} {2}}} {\ Frac {\ Gamma \ lewo ({\ Frac {\ nu +2} {2}} \ prawo)} {\ Gamma \ lewo ( {\ frac {\ nu +3} {2}} \ right)}} \ mu; \,}$

a gdy μ → ∞, tryb jest aproksymowany przez

${\ Displaystyle {\ sqrt {\ Frac {\ nu} {\ nu +1}}} \ mu.}$

Wystąpienia

Zastosowanie w analizie mocy

Załóżmy, że mamy niezależną i identycznie rozłożoną próbkę X ₁ , ..., X _n, z których każda ma rozkład normalny ze średnią θ i wariancją σ ² , i jesteśmy zainteresowani przetestowaniem hipotezy zerowej θ = 0 w porównaniu z hipotezą alternatywną θ ≠ 0. Możemy wykonać jedna próbka t -test stosując statystykę testową

${\ Displaystyle T = {\ Frac {\ bar {X}} {{\ kapelusz {\ sigma}} / {\ sqrt {n}}}} = {\ Frac {{\ Frac {{\ bar {X}} - \ theta} {(\ sigma / {\ sqrt {n}})}} + {\ frac {\ theta} {(\ sigma / {\ sqrt {n}})}}} {\ sqrt {\ left. \ left ({\ frac {{\ hat {\ sigma}} ^ {2}} {\ sigma ^ {2} / (n-1)}} \ right) \ right / (n-1)}}}}$

gdzie jest średnią próbki i nieobciążoną wariancją próbki . Ponieważ prawa strona drugiej równości dokładnie odpowiada charakterystyce niecentralnego rozkładu t, jak opisano powyżej, T ma niecentralny rozkład t z n −1 stopniami swobody i parametrem niecentralności . ${\ displaystyle {\ bar {X}}}$${\ displaystyle {\ hat {\ sigma}} ^ {2} \, \!}$${\ Displaystyle {\ sqrt {n}} \ theta / \ sigma \, \!}$

Jeśli procedura testowa odrzuca hipotezę zerową, ilekroć , gdzie jest górny kwantyl α / 2 (centralnego) rozkładu t- Studenta dla z góry określonego α ∈ (0, 1), to moc tego testu jest określona wzorem${\ Displaystyle | T |> t_ {1- \ alfa / 2} \, \!}$${\ displaystyle t_ {1- \ alpha / 2} \, \!}$

${\ displaystyle 1-F_ {n-1, {\ sqrt {n}} \ theta / \ sigma} (t_ {1- \ alpha / 2}) + F_ {n-1, {\ sqrt {n}} \ theta / \ sigma} (- t_ {1- \ alpha / 2}).}$

Podobnych zastosowań noncentral t -Dystrybucja można znaleźć w analizie mocy ogólnej teoria standardowa liniowego modelu , który zawiera ponad jedną próbkę t -Test jako szczególny przypadek.

Stosować w przedziałach tolerancji

Jednostronne normalne przedziały tolerancji mają dokładne rozwiązanie pod względem średniej próbki i wariancji próbki w oparciu o niecentralny rozkład t- Studenta. Umożliwia to obliczenie przedziału statystycznego, w którym, przy pewnym poziomie ufności, mieści się określony odsetek populacji objętej próbą.

Powiązane dystrybucje

• Centralny rozkład t : centralny rozkład t można przekształcić w rodzinę lokalizacji / skali . Ta rodzina rozkładów jest używana w modelowaniu danych do wychwytywania różnych zachowań ogona. Uogólnienie lokalizacji / skali centralnego rozkładu t jest innym rozkładem niż niecentralny rozkład t omówiony w tym artykule. W szczególności to przybliżenie nie uwzględnia asymetrii niecentralnego rozkładu t . Jednak centralny rozkład t może być użyty jako przybliżenie niecentralnego rozkładu t .
• Jeżeli T jest noncentral t -distributed z ν stopnie swobody i noncentrality parametr ľ i K = T ² , a M ma noncentral F -Dystrybucja ze stopnia 1 licznik swobody, v mianownik stopnia swobody, a parametr noncentrality ľ ² .
• Jeśli T jest niecentralnym t -rozłożonym z ν stopniami swobody i parametrem niecentralności μ , a następnie Z ma rozkład normalny ze średnią μ i jednostkową wariancją. ${\ displaystyle Z = \ lim _ {\ nu \ rightarrow \ infty} T}$
• Gdy mianownik parametr noncentrality z podwójnie noncentral t -Dystrybucja ma wartość zero, wówczas staje się to noncentral t -Dystrybucja.

Przypadki specjalne

• Gdy μ = 0, niecentralny rozkład t- Studenta staje się centralnym rozkładem t- Studenta z tymi samymi stopniami swobody.

Zobacz też

• Noncentral F -Dystrybucja

Bibliografia

Linki zewnętrzne

• Eric W. Weisstein. „Niecentralna dystrybucja t Studenta ”. Z MathWorld - zasobów sieci Web Wolfram
• Wysoka dokładność kalkulacji dla życia lub nauki .: Noncentral t -Dystrybucja z firmy Casio.