Wielokąt Petriego - Petrie polygon
W geometrii , A wielokąta Petrie o regularnym Polytope z n wymiarów jest skośna wielokąt , w którym co ( n - 1) kolejnych boków (ale nie n ) należy do jednej z tych ścianek . Wielokąt Petriego z regularnego wielokąta jest sam regularny wielokąt; że z regularnego wielościanu jest wielokąt skośny takie, że każdy kolejny dwa boczne (ale nie trzy) należy do jednej ze ścian . Wielokąty Petriego zostały nazwane na cześć matematyka Johna Flindersa Petriego .
Dla każdego wielokąta foremnego istnieje rzut ortogonalny na płaszczyznę taki, że jeden wielokąt Petriego staje się wielokątem foremnym z pozostałą częścią wnętrza rzutu do niego. Płaszczyzna, w kwestii jest płaszczyzna Coxeter z grupy symetrii wielokąta, a liczba boków, h, jest ilość Coxeter z grupy Coxeter . Te wielokąty i rzutowane grafy są przydatne do wizualizacji symetrycznej struktury wielowymiarowych regularnych wielokątów.
Wielokąty Petriego mogą być definiowane bardziej ogólnie dla dowolnego osadzonego grafu . Tworzą one powierzchnie innego osadzenia tego samego wykresu, zwykle na innej powierzchni, zwanego dualem Petriego .
Historia
John Flinders Petrie (1907-1972) był jedynym synem egiptologa Flindersa Petrie . Urodził się w 1907 roku i jako uczeń wykazywał niezwykłą obietnicę zdolności matematycznych. W okresach intensywnej koncentracji potrafił odpowiadać na pytania dotyczące skomplikowanych czterowymiarowych obiektów, wizualizując je.
Najpierw zwrócił uwagę na znaczenie regularnych wielokątów skośnych, które pojawiają się na powierzchni wielościanów foremnych i wyższych politopów. Coxeter wyjaśnił w 1937, jak on i Petrie zaczęli rozwijać klasyczny temat wielościanów regularnych:
- Pewnego dnia w 1926 roku JF Petrie powiedział mi z wielkim podekscytowaniem, że odkrył dwa nowe regularne wielościany; nieskończona, ale wolna od fałszywych wierzchołków. Kiedy moje niedowierzanie zaczęło ustępować, opisał mi je: jeden składający się z kwadratów, po sześć na każdym wierzchołku i jeden składający się z sześciokątów, po cztery na każdym wierzchołku.
W 1938 Petrie współpracował z Coxeterem, Patrickiem du Val i HT Flatherem przy produkcji The Fifty-Nine Icosahedra do publikacji. Zdając sobie sprawę z geometrycznej łatwości ukośnych wielokątów używanych przez Petriego, Coxeter nazwał je po swoim przyjacielu, kiedy pisał Regularne wielokąty .
Idea wielokątów Petriego została później rozszerzona na wielokąty półregularne .
Wielokąty Petriego regularnych wielościanów
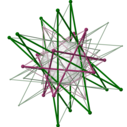
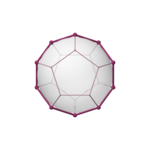
W regularnych Podwójne { P , Q } i { q , s }, są zawarte w tej samej przewidywanego Wielokąt Petriego. Na obrazach podwójnych związków po prawej widać, że ich wielokąty Petriego mają prostokątne przecięcia w punktach, w których krawędzie stykają się ze wspólną kulą środkową .
| Kwadrat | Sześciokąt | Dziesięciobok | ||
|---|---|---|---|---|

|

|

|
|

|
| czworościan {3,3} | kostka {4,3} | ośmiościan {3,4} | dwunastościan {5,3} | dwudziestościan {3,5} |
|
|
|
|
|
|
| wyśrodkowany na krawędzi | wyśrodkowany na wierzchołku | skoncentrowany na twarzy | skoncentrowany na twarzy | wyśrodkowany na wierzchołku |
| V :(4,0) | V :(6,2) | V :(6,0) | V :(10,10,0) | V :(10,2) |
|
Wielokąty Petriego są zewnętrzną stroną tych rzutów ortogonalnych. |
||||
Wielokąty Petriego wielościanu Keplera-Poinsota to sześciokąty {6} i dekagramy {10/3}.
| Sześciokąt | Dekagram | ||
|---|---|---|---|

|

|

|

|
| gD {5,5/2} | SD {5,5/2} | gI {3,5/2} | gsD {5/2,3} |
|
|
|
|
|
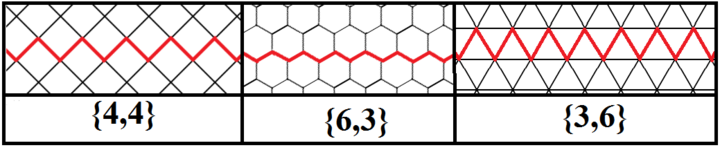
Nieskończone regularne wielokąty skośne ( apeirogon ) można również zdefiniować jako wielokąty Petriego regularnych płytek, o kątach 90, 120 i 60 stopni odpowiednio ich kwadratowej, sześciokątnej i trójkątnej powierzchni.
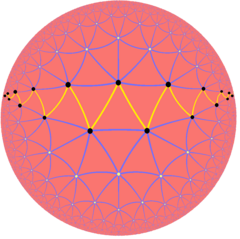
Nieskończone regularne wielokąty skośne istnieją również jako wielokąty Petriego regularnych płytek hiperbolicznych, takich jak trójkątne płytki rzędu 7 , {3,7}:
Wielokąt Petriego regularnej polichory (4-politopy)
Można również wyznaczyć wielokąt Petriego dla wielochor regularnych { p , q , r }.
 {3,3,3} 5-komorowy 5 stron V :(5,0) |
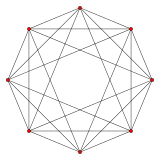 {3,3,4} 16-komorowy 8 stron V :(8,0) |
 {4,3,3} tesseract 8 stron V :(8,8,0) |
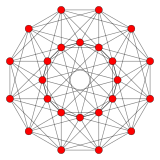 {3,4,3} 24-ogniwowy 12 stron V :(12,6,6,0) |
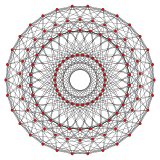 {3,3,5} 600 ogniw 30 stron V:(30,30,30,30,0) |
 {5,3,3} 120 ogniw 30 stron V :((30,60) 3 ,60 3 ,30,60,0) |
Rzuty wielokątów Petriego regularnych i jednorodnych politopów
Rzuty wielokątów Petriego są przydatne do wizualizacji wielokątów o wymiarze czwartym i wyższym.
Hipersześciany
Hipersześcian wymiaru n ma Wielokąt Petriego o wielkości 2, n , który jest również liczba jego aspektach .
Tak więc każdy z sześcianów ( n -1) tworzących jego powierzchnię ma n -1 boków wielokąta Petriego pomiędzy swoimi krawędziami.
| Hipersześciany | ||
|---|---|---|
|
Digon Petriego na kostce 1 wygląda identycznie jak kostka 1 . Ale 1-sześcian ma jedną krawędź, podczas gdy digon ma dwie.
(Dla n =1 pierwsza i druga połowa to dwie odrębne, ale pokrywające się krawędzie dwukąta.)
|
||
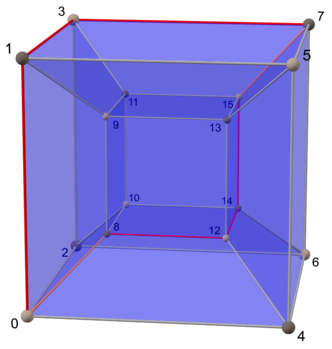
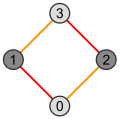
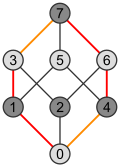
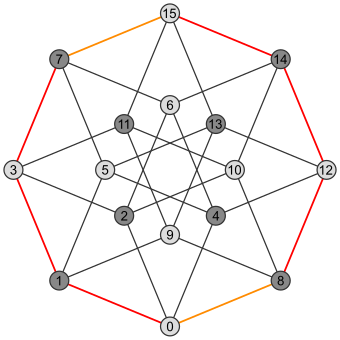
| Kwadrat | Sześcian | Teserakt |

|
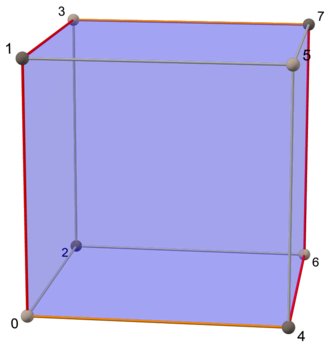
|
|
|
|
|
Nieredukowalne rodziny politopów
Ta tabela przedstawia rzuty wielokątów Petriego 3 rodzin regularnych ( simpleks , hipersześcian , ortopleks ) i wyjątkową grupę Liego E n, które generują półregularne i jednolite wielokąty dla wymiarów od 4 do 8.
| Tabela nieredukowalnych rodzin politopów | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rodzina nr |
n- simpleks | n- hipersześcian | n- ortopleks | n- demicube | 1 k2 | 2 k1 | k 21 | wielokąt pięciokątny | ||||||||
| Grupa | A n | B n |
|
|
H n | |||||||||||
| 2 |
 |
 |
 p-gon (przykład: p=7 ) |
 Sześciokąt |
 Pięciokąt |
|||||||||||
| 3 |
 Czworościan |
 Sześcian |
 Oktaedr |
 Czworościan |
 Dwunastościan |
 dwudziestościan |
||||||||||
| 4 |
 5-ogniwowy |
 |
 16-ogniwowy |
 |
 24-komorowy |
 120-ogniwowy |
 600-ogniwowy |
|||||||||
| 5 |
 5-simplex |
 5-kostka |
 5-ortopleks |
 5-demicube |
||||||||||||
| 6 |
 6-simplex |
 6-kostek |
 6-ortopleks |
 6-demicube |
 1 22 |
 2 21 |
||||||||||
| 7 |
 7-simplex |
 7-kostka |
 7-ortopleks |
 7-demicube |
 1 32 |
 2 31 |
 3 21 |
|||||||||
| 8 |
 8-simplex |
 8-kostka |
 8-ortopleks |
 8-demicube |
 1 42 |
 2 41 |
 4 21 |
|||||||||
| 9 |
 9-simplex |
 9-kostka |
 9-ortopleks |
 9-demicube |
||||||||||||
| 10 |
 10-simplex |
 10 kostek |
 10-ortopleks |
 10-demicube |
||||||||||||
Uwagi
Bibliografia
- Coxeter , HSM (1947, 63, 73) Regular Polytopes , wyd. New York: Dover, 1973. (sek. 2.6 Petrie Polygons, s. 24-25 i Rozdział 12, s. 213-235, Uogólniony wielokąt Petriego )
- Coxeter, HSM (1974) Regularne złożone politopy . Sekcja 4.3 Flagi i ortoschemy, Sekcja 11.3 Wielokąty Petriego
- Ball, WWR i HSM Coxeter (1987) Mathematical Recreations and Essays , 13th ed. Nowy Jork: Dover. (s. 135)
- Coxeter, HSM (1999) Piękno geometrii: dwanaście esejów , publikacje Dover LCCN 99-35678
- Peter McMullen , Egon Schulte (2002) Abstrakcyjne Polytopes Regularne , Cambridge University Press . ISBN 0-521-81496-0
- Steinberg, Robert, O ILOŚCI STRON WIELOKĄTA PETRIEGO
Zobacz też
Zewnętrzne linki
- Weisstein, Eric W. „Wielokąt Petriego” . MatematykaŚwiat .
- Weisstein, Eric W. „Wykresy hipersześcianów” . MatematykaŚwiat .
- Weisstein, Eric W. „Krzyżowe wykresy wielotopowe” . MatematykaŚwiat .
- Weisstein, Eric W. „Wykres 24-komórkowy” . MatematykaŚwiat .
- Weisstein, Eric W. „Wykres 120 komórek” . MatematykaŚwiat .
- Weisstein, Eric W. „Wykres 600 komórek” . MatematykaŚwiat .
- Weisstein, Eric W. "Wykres Gosset 3_21" . MatematykaŚwiat .