Lemat o wężu - Snake lemma

Wąż lemat to narzędzie w matematyce , zwłaszcza homologicznej Algebra celu skonstruowania długości dokładnie sekwencji . Lemat węża jest ważny w każdej kategorii abelowej i jest kluczowym narzędziem w algebrze homologicznej i jej zastosowaniach, na przykład w topologii algebraicznej . Homomorfizmy konstruowane za jego pomocą nazywane są ogólnie homomorfizmami łączącymi .

Komunikat

W kategorii abelowej (takiej jak kategoria grup abelowych lub kategoria przestrzeni wektorowych nad danym ciałem ) rozważ diagram przemienny :

gdzie wiersze są dokładnymi sekwencjami, a 0 jest obiektem zerowym .

Wtedy nie jest dokładna kolejność odnoszące się jąder i cokernels z a , b i c :

${\ Displaystyle \ ker a~ {\ kolor {szary} \ longrightarrow} ~ \ ker b ~ {\ kolor {szary} \ longrightarrow} ~ \ ker c ~ ​​{\ przesłonięty {d} {\ longrightarrow}} ~ \ nazwa operatora { coker} a~{\color {gray}\longrightarrow }~\operatorname {coker} b~{\color {gray}\longrightarrow }~\operatorname {coker} c}$

gdzie d jest homomorfizmem, znanym jako homomorfizm łączący .

Co więcej, jeśli morfizm f jest monomorfizmem , to taki jest morfizm , a jeśli g' jest epimorfizmem , to taki jest . ${\ Displaystyle \ ker a ~ {\ kolor {szary} \ longrightarrow} ~ \ ker b}$${\displaystyle \operatorname {coker} b~{\color {gray}\longrightarrow}~\operatorname {coker} c}$

Kokardki tutaj to: , , . ${\displaystyle \operatorname {coker} a=A'/\operatorname {im} a}$${\displaystyle \operatorname {coker} b = B'/\operatorname {im} b}$${\displaystyle \operatorname {coker} c=C'/\operatorname {im} c}$

Wyjaśnienie nazwy

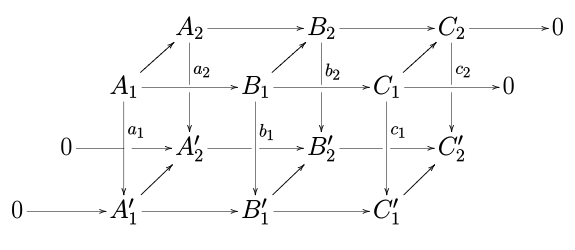
Aby zobaczyć, skąd wziął się lemat o wężu, rozwiń powyższy diagram w następujący sposób:

a następnie zauważ, że dokładną sekwencję, która jest konkluzją lematu, można narysować na tym rozszerzonym schemacie w kształcie odwróconego „S” pełzającego węża .

Budowa map

Mapy pomiędzy jądrami i mapy pomiędzy kokernelami są indukowane w naturalny sposób przez dane (horyzontalne) mapy ze względu na przemienność diagramu. Dokładność dwóch indukowanych sekwencji wynika w prosty sposób z dokładności rzędów oryginalnego diagramu. Ważnym stwierdzeniem tego lematu jest to, że istnieje łączący homomorfizm d , który uzupełnia dokładną sekwencję.

W przypadku grup abelowych lub modułów nad jakimś pierścieniem , mapę d można skonstruować w następujący sposób:

Wybierz element x w ker  c i zobacz go jako element C ; ponieważ g jest surjektywne , istnieje y w B z g ( y ) = x . Ze względu na przemienność diagramu mamy g' ( b ( y )) = c ( g ( y )) = c ( x ) = 0 (ponieważ x jest w jądrze c ), a zatem b ( y ) jest w jądrze g' . Ponieważ dolny wiersz jest dokładny, znajdujemy element z w A' z f  '( z ) = b ( y ). z jest unikalny przez wstrzykiwanie f  '. Następnie definiujemy d ( x ) = z + im ( a ). Teraz trzeba sprawdzić, czy d jest dobrze zdefiniowane (tj. d ( x ) zależy tylko od x, a nie od wyboru y ), że jest to homomorfizm i czy otrzymana długa sekwencja jest rzeczywiście dokładna. Dokładność można rutynowo weryfikować, śledząc diagram (patrz dowód Lematu 9.1 w ).

Gdy to zrobisz, twierdzenie zostanie udowodnione dla grup abelowych lub modułów w pierścieniu. W przypadku ogólnym argument można przeformułować pod kątem właściwości strzałek i anulowania zamiast elementów. Alternatywnie można odwołać się do twierdzenia Mitchella o osadzeniu .

Naturalność

W aplikacjach często trzeba wykazać, że długie, dokładne ciągi są „naturalne” (w sensie przekształceń naturalnych ). Wynika to z naturalności sekwencji tworzonej przez lemat węża.

Gdyby

jest diagramem przemiennym z dokładnymi rzędami, to lemat węża można zastosować dwukrotnie, na „przód” i „z tyłu”, dając dwie długie, dokładne sekwencje; są one powiązane przemiennym diagramem postaci

Przykład

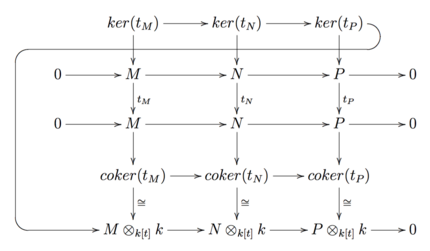
Niech będzie polem, będzie przestrzenią wektorową. jest -module przez bycie -linear transformacja, więc możemy tensora i ponad . ${\displaystyle k}$${\ Displaystyle V}$${\displaystyle k}$${\ Displaystyle V}$${\displaystyle k[t]}$${\displaystyle t:V\doV}$${\displaystyle k}$${\ Displaystyle V}$${\displaystyle k}$${\displaystyle k[t]}$

${\ Displaystyle V \ otimes _ {k [t]} k = V \ otimes _ {k [t]} (k [t] / (t)) = V / tV = \ operatorname {kokser} (t).}$

Mając krótki, dokładny ciąg przestrzeni -wektorowych , możemy indukować dokładny ciąg przez odpowiednią dokładność iloczynu tensorowego. Ale ogólnie kolejność nie jest dokładna. Powstaje więc naturalne pytanie. Dlaczego ta sekwencja nie jest dokładna? ${\displaystyle k}$${\ Displaystyle 0 \ do M \ do N \ do P \ do 0}$${\ Displaystyle M \ otimes _ {k [t]} k \ do N \ otimes _ {k [t]} k \ do P \ otimes _ {k [t]} k \ do 0}$${\ Displaystyle 0 \ do M \ otimes _ {k [t]} k \ do N \ otimes _ {k [t]} k \ do P \ otimes _ {k [t]} k \ do 0}$

Zgodnie z powyższym diagramem możemy wywołać dokładną sekwencję , stosując lemat węża. Zatem lemat węża odzwierciedla niedokładność iloczynu tensorowego. ${\ Displaystyle \ ker (t_ {M}) \ do \ ker (t_ {N}) \ do \ ker (t_ {P}) \ do M \ czasami _ {k [t]} k \ do N \ czasami _ {k[t]}k\to P\otimes _{k[t]}k\to 0}$

W kulturze popularnej

Dowodu na istnienie lematu o wężu uczy bohaterka Jill Clayburgh na samym początku filmu z 1980 r. To moja kolej .

Zobacz też

• Lemat zygzakowaty

Bibliografia

• Serge Lang : Algebra . Wydanie trzecie, Springer 2002, ISBN  978-0-387-95385-4 , s. 157-159 ( kopia online , s. 157, w Google Books )
• MF Atiyah ; IG Macdonald : Wprowadzenie do algebry przemiennej . Oxford 1969, Addison-Wesley Publishing Company, Inc. ISBN  0-201-00361-9 .
• P. Hiltona; U. Stammbach: Kurs algebry homologicznej. 2. Auflage, Springer Verlag, Graduate Texts in Mathematics , 1997, ISBN  0-387-94823-6 , s. 99 ( kopia online , s. 99, w Google Books )

Linki zewnętrzne

• Weisstein, Eric W. „Lemat węża” . MatematykaŚwiat .
• Lemat o wężu w PlanetMath
• Dowód lematu o wężu w filmie To moja kolej