Składnia i symbole APL - APL syntax and symbols
Język programowania APL wyróżnia się tym, że jest raczej symboliczny niż leksykalny : jego prymitywy są oznaczane przez symbole , a nie słowa. Symbole te zostały pierwotnie opracowane jako notacja matematyczna do opisywania algorytmów. Programiści APL często przypisują nieformalne nazwy podczas omawiania funkcji i operatorów (na przykład iloczyn dla ×/), ale podstawowe funkcje i operatory dostarczane przez język są oznaczone symbolami nietekstowymi.
Funkcje monadyczne i diadyczne
Większość symboli oznacza funkcje lub operatory . Funkcja monadyczna przyjmuje jako argument wynik oceny wszystkiego po swojej prawej stronie. (Moderowana w zwykły sposób przez nawiasy). Funkcja dwumianowa ma kolejny argument, pierwszą pozycję danych po lewej stronie. Wiele symboli oznacza zarówno funkcje monadyczne, jak i diadyczne, interpretowane zgodnie z użyciem. Na przykład 3,2 daje 3, największą liczbę całkowitą nie powyżej argumentu, a 3⌊2 daje 2, niższy z dwóch argumentów.
Funkcje i operatory
APL używa terminu operator w znaczeniu Heaviside'a jako moderatora funkcji, w przeciwieństwie do użycia tego samego terminu w innym języku programowania jako czegoś, co operuje na danych, ref. operator relacyjny i operatory ogólnie . Inne języki programowania również czasami używają tego terminu zamiennie z function , jednak oba terminy są używane dokładniej w APL. Wczesne definicje symboli APL były bardzo szczegółowe w odniesieniu do kategoryzacji symboli. Na przykład operator zmniejszyć jest oznaczony ukośnikiem i zmniejsza tablicę wzdłuż jednej osi, wstawiając swoją funkcję operand . Przykład redukcji :
×/2 3 4 24 |
<< Równoważne wyniki w APL >> << Zmniejsz operator / używany z lewej |
2×3×4 24 |
W powyższym przypadku operator zmniejszania lub ukośnika moderuje funkcję mnożenia . Wyrażenie ×/2 3 4 daje wynik skalarny (tylko 1 element) poprzez zmniejszenie tablicy przez mnożenie. Powyższy przypadek jest uproszczony, wyobraź sobie mnożenie (dodawanie, odejmowanie lub dzielenie) więcej niż tylko kilku liczb. (Z wektora x/ zwraca iloczyn wszystkich jego elementów.)
1 0 1\45 67 45 0 67 |
<< Przeciwne wyniki w APL >> << Rozwiń funkcję dwójkowym \ używany na lewym Replikuj funkcji diadycznej / używane po prawej stronie >> |
1 0 1/45 0 67 45 67 |
Powyższy dwójkowym funkcji Przykłady [lewy i prawy przykłady] (przy użyciu tego samego / symbol, tuż przykład) pokazują, jak logiczna wartości (0 i 1) mogą być używane jako lewy argumentów dla \ rozszerzyć i / replikowanych funkcje w celu wytworzenia dokładnie odwrotne wyniki. Po lewej stronie dwuelementowy wektor {45 67} jest rozwijany, gdzie logiczne zera dają w wyniku trzyelementowy wektor {45 0 67} — zauważ, jak APL wstawił 0 do wektora. I odwrotnie, dokładnie odwrotnie występuje po prawej stronie — gdzie wektor 3-elementowy staje się tylko 2-elementowym; wartości logiczne zer usuwają elementy za pomocą funkcji dwumiany / ukośnika . Symbole APL działają również na listach (wektorach) elementów używających typów danych innych niż tylko numeryczne, na przykład 2-elementowy wektor ciągów znaków {"Jabłka" "Pomarańcze"} mógłby zostać zastąpiony wektorem numerycznym {45 67} powyżej.
Zasady składni
W APL nie ma hierarchii pierwszeństwa dla funkcji lub operatorów. APL nie stosuje zwykłego pierwszeństwa operatorów innych języków programowania; na przykład ×nie wiąże swoich operandów bardziej „ściśle” niż +. Zamiast pierwszeństwa operatorów, APL definiuje pojęcie scope .
Zakres z funkcji określa swoje argumenty . Funkcje mają długi właściwy zakres : to znaczy, jako właściwe argumenty przyjmują wszystko, co jest im właściwe. Funkcja dwójkowa ma krótki lewy zasięg : jako swoje lewe argumenty przyjmuje pierwszą część danych po jej lewej stronie. Na przykład (lewa kolumna poniżej to rzeczywisty kod programu z sesji użytkownika APL , wcięcie = rzeczywiste dane wprowadzone przez użytkownika , bez wcięcia = wynik zwrócony przez interpreter APL ):
1 ÷ 2 ⌊ 3 × 4 - 5
¯0.3333333333
1 ÷ 2 ⌊ 3 × ¯1
¯0.3333333333
1 ÷ 2 ⌊ ¯3
¯0.3333333333
1 ÷ ¯3
¯0.3333333333
|
<< Po pierwsze, nie ma nawiasów, a Krok 2) 3 razy -1 = -3. |
Operator może mieć funkcję lub operandy danych i szacować do funkcji dwójkowej lub monadycznej. Operatorzy już dawno opuścili zakres. Operator przyjmuje jako lewy operand najdłuższą funkcję po jego lewej stronie. Na przykład:
∘.=/⍳¨3 3 1 0 0 0 1 0 0 0 1
|
APL atomowej lub na części pod-analiza ( Pełne wyjaśnienie ) Diaeresis ¨ lub mini dwukrotnie kropka oznacza powtórzenie lub nad sobą lub wykonać osobno tak jota powtórzenia (w ludzki czyli odwrócone warunki, interpreter APL czyta 3 3 nad każdym użyciu jota), zwięźle: jotę dla każdego 3 . |
Lewy argument do nadmiernego każdy operator ¨jest wskaźnik ⍳ funkcję. Funkcja pochodzi ⍳¨ służy monadically i przyjmuje jako argumentu jej prawa wektora 3 3. Lewy zakres każdego jest zakończony operatorem redukcji oznaczonym ukośnikiem . Jego lewy argument jest wyrażeniem funkcja jego lewo: zewnętrzna produkt z równa funkcji. Wynik ∘.=/ jest funkcją monadyczną. W przypadku zwykłego długiego prawego zakresu funkcji, jako prawy argument przyjmuje wynik ⍳¨3 3. Zatem
(⍳3)(⍳3)
1 2 3 1 2 3
(⍳3)∘.=⍳3
1 0 0
0 1 0
0 0 1
⍳¨3 3
1 2 3 1 2 3
∘.=/⍳¨3 3
1 0 0
0 1 0
0 0 1
|
Macierz jedynek i zer podobnie wytworzona przez Macierze tożsamości są przydatne w rozwiązywaniu wyznaczników macierzowych , grup równań liniowych i regresji wielokrotnej . |
im ← ∘.=⍨∘⍳
im 3
1 0 0
0 1 0
0 0 1
|
Niektórzy tłumacze APL wspieranie tworzenia, operator ∘ i dojeżdżać operatora ⍨ . Poprzednie ∘ skleja funkcje, tak że na przykład foo∘bar może być hipotetyczną funkcją, która stosuje zdefiniowaną funkcję foo do wyniku zdefiniowanej funkcji bar ; foo i bar mogą reprezentować dowolną istniejącą funkcję. W przypadkach, w których dwójkowym funkcja jest moderowana przez dojazdy , a następnie wykorzystywane monadically, jego prawo argumentem jest traktowana jako swojego lewego argumentu, jak również. Tak więc funkcja pochodna lub złożona (o nazwie im po lewej stronie) jest używana w sesji użytkownika APL do zwrócenia 9- elementowej macierzy tożsamości przy użyciu jej prawego argumentu , parametru lub operandu = 3. |
Letters←"ABCDE"
Letters
ABCDE
⍴Letters
5
FindIt←"CABS"
FindIt
CABS
⍴FindIt
4
Letters ⍳ FindIt
3 1 2 6
|
Przykład użycia APL do indeksowania ⍳ lub znajdowania (lub nie znajdowania) elementów w wektorze znakowym : Po pierwsze, zmiennej Letters przypisywany jest wektor składający się z 5 elementów, w tym przypadku - liter alfabetu. Kształt ⍴ lub postaci wektora długości Letters to 5. Zmienna FindIt jest przypisana do czego szukać w listach, a jej długość to 4 znaki. 1 2 3 4 5 << pozycji wektora lub Wskaźnik 'sw Letters Po lewej stronie funkcja dwuczłonowa iota przeszukuje swój lewy argument (Litery) w poszukiwaniu szukanego ciągu (prawy argument iota, FindIt). Jota znajduje się litera „C” w pozycji 3 Letters, stwierdzi, „A” w pozycji 1, a „B” w pozycji 2 jota ma odnaleźć litery „S” gdziekolwiek w zmiennej Letters, więc zwraca liczbę 6, która jest o 1 większa niż długość Letters. Iota znalazła litery „KABINA” (3 1 2). Iota poprawnie nie znalazła „S” (6). |
Funkcje monadyczne
| Nazwy) | Notacja | Znaczenie | Punkt kodu Unicode |
|---|---|---|---|
| Rolka |
?B
|
Jedna liczba całkowita wybrana losowo z pierwszych B liczb całkowitych | U+003F ? |
| Sufit |
⌈B
|
Najmniejsza liczba całkowita większa lub równa B | U + 2308 ⌈ |
| Piętro |
⌊B
|
Największa liczba całkowita mniejsza lub równa B | U + 230A ⌊ |
| Kształt, Rho |
⍴B
|
Liczba elementów w każdym wymiarze B | U + 2374 ⍴ |
| Nie , tylda |
∼B
|
Logiczne: ∼1 to 0, ∼0 to 1 | U+223C ∼ |
| Całkowita wartość |
∣B
|
Wielkość B | U + 2223 | |
| Generator indeksów, Iota |
⍳B
|
Wektor pierwszych B liczb całkowitych | U + 2373 ⍳ |
| Wykładniczy |
⋆B
|
e do potęgi B | U + 22C6 |
| Negacja |
−B
|
Zmienia znak B | U+2212 − |
| Sprzężony |
+B
|
Złożona koniugat B (liczby rzeczywiste są zwracane bez zmian) | U+002B + |
| Signum |
×B
|
¯1 jeśli B <0; 0 jeśli B =0; 1 jeśli B >0 | U+00D7 × |
| Odwrotność |
÷B
|
1 podzielone przez B | U+00F7 ÷ |
| Ravel, Catenate, Laminat |
,B
|
Przekształca B w wektor | U+002C , |
| Macierz odwrotna , monadyczny podział czwórkowy |
⌹B
|
Odwrotność macierzy B | U + 2339 ⌹ |
| Pi razy |
○B
|
Pomnóż przez π | U+25CB ○ |
| Logarytm |
⍟B
|
Logarytm naturalny B | U + 235F ⍟ |
| Odwrócenie |
⌽B
|
Odwróć elementy B wzdłuż ostatniej osi | U+ 233D |
| Odwrócenie |
⊖B
|
Odwróć elementy B wzdłuż pierwszej osi | U + 2296 ⊖ |
| Stopniowanie |
⍋B
|
Indeksy B, które ułożą B w porządku rosnącym | U + 234B ⍋ |
| Niższa ocena |
⍒B
|
Indeksy B, które ułożą B w porządku malejącym | U + 2352 ⍒ |
| Wykonać |
⍎B
|
Wykonaj wyrażenie APL | U+ 234E |
| Format monadyczny |
⍕B
|
Reprezentacja znakowa B | U + 2355 ⍕ |
| Transpozycja monadyczna |
⍉B
|
Odwróć osie B | U + 2349 ⍉ |
| Factorial |
!B
|
Iloczyn liczb całkowitych od 1 do B | U+0021 ! |
Funkcje dwójkowe
| Nazwy) | Notacja | Znaczenie | Punkt kodu Unicode |
|---|---|---|---|
| Dodaj |
A+B
|
Suma A i B | U+002B + |
| Odejmować |
A−B
|
Minus B | U+2212 − |
| Zwielokrotniać |
A×B
|
A pomnożone przez B | U+00D7 × |
| Podzielić |
A÷B
|
Podzielona przez B | U+00F7 ÷ |
| Potęgowanie |
A⋆B
|
A podniesione do potęgi B | U + 22C6 |
| okrąg |
A○B
|
Funkcje trygonometryczne B wybrane przez A
A=1: sin(B) A=5: sinh(B) A=2: cos(B) A=6: cosh(B) A=3: tan(B) A=7: tanh(B) Negatywy tworzą odwrotność odpowiednich funkcji |
U+25CB ○ |
| Rozdać |
A?B
|
A różne liczby całkowite, wybranych losowo z pierwszych B liczb | U+003F ? |
| Członkostwo, Epsilon |
A∈B
|
1 dla elementów A obecnych w B ; 0 gdzie nie. | U + 2208 ∈ |
| Znajdź, Epsilon Underbar |
A⍷B
|
1 dla punktu początkowego wieloelementowej tablicy A występującej w B ; 0 gdzie nie. | U + 2377 ⍷ |
| Maksimum , Pułap |
A⌈B
|
Większa wartość A lub B | U + 2308 ⌈ |
| Minimalna , piętro |
A⌊B
|
Mniejsza wartość A lub B | U + 230A ⌊ |
| Przekształć, Dwójkowy Rho |
A⍴B
|
Tablica kształtu A z danymi B | U + 2374 ⍴ |
| Brać |
A↑B
|
Wybierz pierwsze (lub ostatnie) elementy A z B zgodnie z × A | U + 2191 ↑ |
| Upuszczać |
A↓B
|
Usuń pierwsze (lub ostatnie) elementy A z B zgodnie z × A | U + 2193 ↓ |
| Rozszyfrować |
A⊥B
|
Wartość wielomianu o współczynnikach B przy A at | U + 22A5 ⊥ |
| Kodować |
A⊤B
|
Base- reprezentacja wartości B | U + 22A4 |
| Pozostałość |
A∣B
|
B Modulo | U + 2223 | |
| Wiązanie |
A,B
|
Elementy B dołączone do elementów A | U+002C , |
| Rozszerzenie, dwudniowy ukośnik odwrotny |
A\B
|
Wstaw zera (lub puste miejsca) w B odpowiadające zerom w A | U + 005C \ |
| Kompresja, ukośnik diadyczny |
A/B
|
Wybierz elementy w B odpowiadające elementom w A | U+002F / |
| Indeks, Dwójkowy Iota |
A⍳B
|
Lokalizacja (indeks) B w A ; jeśli nie znaleziono
1+⍴A |
U + 2373 ⍳ |
| Dzielenie macierzy, dzielenie czterodwudzielne |
A⌹B
|
Rozwiązanie układu równań liniowych , regresja wielokrotna A x = B | U + 2339 ⌹ |
| Obrót |
A⌽B
|
Elementy B są obrócone A pozycje | U+ 233D |
| Obrót |
A⊖B
|
Elementy B są obrócone A pozycje wzdłuż pierwszej osi | U + 2296 ⊖ |
| Logarytm |
A⍟B
|
Logarytm z B do bazy A | U + 235F ⍟ |
| Format dwudniowy |
A⍕B
|
Sformatuj B do macierzy znaków zgodnie z A | U + 2355 ⍕ |
| Ogólna transpozycja |
A⍉B
|
Osie B są uporządkowane według A | U + 2349 ⍉ |
| Kombinacje |
A!B
|
Liczba kombinacji B wziętych A na raz | U+0021 ! |
| Diereza, diereza, podwójna kropka |
A¨B
|
Nad każdym lub wykonaj każdy osobno; B = na tych; A = operacja do wykonania lub użycia (np. iota) | U + 00A8 ¨ |
| Mniej niż |
A < B
|
Porównanie: 1 jeśli prawda, 0 jeśli fałsz | U+003C < |
| Mniejsze lub równe |
A≤B
|
Porównanie: 1 jeśli prawda, 0 jeśli fałsz | U + 2264 ≤ |
| Równy |
A=B
|
Porównanie: 1 jeśli prawda, 0 jeśli fałsz | U+003D = |
| Większe lub równe |
A≥B
|
Porównanie: 1 jeśli prawda, 0 jeśli fałsz | U+2265 ≥ |
| Lepszy niż |
A>B
|
Porównanie: 1 jeśli prawda, 0 jeśli fałsz | U+003E > |
| Nie równe |
A≠B
|
Porównanie: 1 jeśli prawda, 0 jeśli fałsz | U+2260 ≠ |
| Lub |
A∨B
|
Operacji logicznych: 0 (fałsz) w przypadku zarówno i B = 0 , 1 inaczej. Alt: 1 (prawda), jeśli A lub B = 1 (prawda) | U + 2228 ∨ |
| I |
A∧B
|
Logika Boole'a: 1 (prawda), jeśli zarówno A, jak i B = 1 , 0 (fałsz) w przeciwnym razie | U + 2227 ∧ |
| Ani |
A⍱B
|
Logika Boole'a: 1 jeśli A i B mają wartość 0, w przeciwnym razie 0. Alt: ~∨ = nie Or | U + 2371 ⍱ |
| Nand |
A⍲B
|
Logika Boole'a: 0 jeśli A i B to 1, w przeciwnym razie 1. Alt: ~∧ = nie And | U + 2372 ⍲ |
| Lewo |
A⊣B
|
ZA | U + 22A3 ⊣ |
| Dobrze |
A⊢B
|
b | U + 22a2 ⊢ |
Operatory i wskaźnik osi
| Nazwy) | Symbol | Przykład | Znaczenie (na przykład) | Sekwencja punktów kodu Unicode |
|---|---|---|---|---|
| Zmniejsz (ostatnia oś), Slash | / |
+/B
|
Suma w poprzek B | U+002F / |
| Zmniejsz (pierwsza oś) | ⌿ |
+⌿B
|
Zsumuj B | U+ 233F |
| Skanuj (ostatnia oś), ukośnik odwrotny | \ |
+\B
|
Suma biegnąca przez B | U + 005C \ |
| Skanowanie (pierwsza oś) | ⍀ |
+⍀B
|
Bieżąca suma B | U+2340 ⍀ |
| Produkt wewnętrzny | . |
A+.×B
|
Produkt matryca z A i B | U+002E . |
| Produkt zewnętrzny | . |
A∘.×B
|
Zewnętrzny iloczyn z A i B | U + 2218 ∘ , U+002E . |
Uwagi: Operatory zmniejszania i skanowania oczekują funkcji dwuczłonowej po lewej stronie, tworzącej monadyczną funkcję złożoną stosowaną do wektora po jego prawej stronie.
Operator produktu „.” oczekuje funkcji dwuczłonowej zarówno po lewej, jak i po prawej stronie, tworząc złożoną funkcję dwuczłonową stosowaną do wektorów po jego lewej i prawej stronie. Jeśli funkcją po lewej stronie kropki jest „∘” (oznaczająca null), to funkcja złożona jest iloczynem zewnętrznym, w przeciwnym razie jest iloczynem wewnętrznym. Iloczyn skalarny przeznaczony do konwencjonalnego mnożenia macierzy wykorzystuje funkcje + i ×, zastąpienie ich innymi funkcjami dwumianowymi może skutkować użytecznymi operacjami alternatywnymi.
Po niektórych funkcjach może występować wskaźnik osi w nawiasach (kwadratowych), tzn. pojawia się on między funkcją a tablicą i nie powinien być mylony z indeksami tablicy zapisywanymi po tablicy. Na przykład, biorąc pod uwagę funkcję ⌽ (odwrócenie) i dwuwymiarową tablicę, funkcja domyślnie działa wzdłuż ostatniej osi, ale można to zmienić za pomocą wskaźnika osi:
A←4 3⍴⍳12
A
1 2 3
4 5 6
7 8 9
10 11 12
⌽A
3 2 1
6 5 4
9 8 7
12 11 10
⌽[1]A
10 11 12
7 8 9
4 5 6
1 2 3
⊖⌽A
12 11 10
9 8 7
6 5 4
3 2 1
⍉A
1 4 7 10
2 5 8 11
3 6 9 12
|
A jest teraz odbijane lub odwracane wzdłuż osi pionowej, jak wskazuje symbol ⌽ . A jest teraz odzwierciedlane za pomocą wskaźnika osi [1] lub modyfikatora pierwszego wymiaru . W rezultacie zmienna A została odbita w poprzek osi poziomej, a nie w pionie. A jest teraz odbijane zarówno pionowo ⊖, jak i poziomo ⌽ . A jest ⍉ transponowane na macierz 3 wiersze na 4 kolumny tak, że wiersze-kolumny zostają zamienione, jak symbol ⍉ przedstawia wizualnie. Porównaj wynik tutaj z oryginalną macierzą zapisaną w A, najwyższej macierzy. Tego typu przekształceń danych są użyteczne w serii czas analizy i współrzędnych przestrzennych , tylko dwa przykłady, koniec istnienia . |
W szczególnym przypadku, jeśli po funkcji dwukanatu "," następuje wskaźnik osi (lub modyfikator osi symbolu/funkcji), można go użyć do laminowania (wstawiania) dwóch tablic w zależności od tego, czy wskaźnik osi jest mniejszy niż lub większe niż początek indeksu (początek indeksu = 1 na ilustracji poniżej):
B←1 2 3 4
C←5 6 7 8
B,C
1 2 3 4 5 6 7 8
B,[0.5]C
1 2 3 4
5 6 7 8
B,[1.5]C
1 5
2 6
3 7
4 8
|
Po lewej stronie zmiennej 'B' najpierw przypisywany jest wektor 4 kolejnych liczb całkowitych (np. ⍳4 ). |
Tablice zagnieżdżone
Tablice to struktury, które mają elementy zgrupowane liniowo jako wektory lub w formie tabeli jako macierze - i wyższe wymiary (3D lub sześcienne, 4D lub sześcienne w czasie itp.). Tablice zawierające zarówno znaki, jak i liczby są nazywane tablicami mieszanymi . Struktury tablicowe zawierające elementy będące jednocześnie tablicami nazywane są tablicami zagnieżdżonymi .
| Sesja użytkownika z interpreterem APL | Wyjaśnienie |
|---|---|
X←4 5⍴⍳20
X
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
16 17 18 19 20
X[2;2]
7
⎕IO
1
X[1;1]
1
|
Element X[2;2] w wierszu 2 - kolumna 2 jest obecnie liczbą całkowitą = 7 . Początkowy początek indeksu ⎕IO wartość = 1 . Zatem pierwszy element macierzy X lub X[1;1] = 1 . |
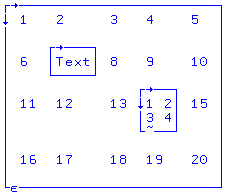
X[2;2]←⊂"Text"
X[3;4]←⊂(2 2⍴⍳4)
X
1 2 3 4 5
6 Text 8 9 10
11 12 13 1 2 15
3 4
16 17 18 19 20
|
Element w X[wiersz 2; col 2] jest zmieniany (z 7) na zagnieżdżony wektor "Tekst" przy użyciu funkcji enclose ⊂ . Element w X[wiersz 3; col 4], dawniej liczba całkowita 14, teraz staje się małą zamkniętą lub zagnieżdżoną macierzą 2x2 4 kolejnych liczb całkowitych. Ponieważ X zawiera liczby , tekst i elementy zagnieżdżone , jest to zarówno tablica mieszana, jak i zagnieżdżona . |
Kontrola przepływu
Użytkownik może definiować własne funkcje , które, podobnie jak zmienne, są identyfikowane przez nazwę zamiast przez non-tekstowej symbolem. W nagłówku funkcji określa, czy funkcja zwyczaj niladic (bez argumentów), monadycznego (jeden prawy argument) lub dwójkowym (lewy i prawy argumenty), lokalna nazwa wyniku (na lewo od ← przypisać strzałka), i czy ma dowolne zmienne lokalne (każda oddzielona średnikiem ';').
| Funkcja Niladowa PI lub π(pi) | Funkcja monadyczna CIRCLEAREA | Dwójkowym funkcja SEGMENTAREA ze zmiennych lokalnych |
|---|---|---|
∇ RESULT←PI
RESULT←○1
∇
|
∇ AREA←CIRCLEAREA RADIUS
AREA←PI×RADIUS⋆2
∇
|
∇ AREA←DEGREES SEGMENTAREA RADIUS ; FRACTION ; CA
FRACTION←DEGREES÷360
CA←CIRCLEAREA RADIUS
AREA←FRACTION×CA
∇
|
To, czy funkcje o tym samym identyfikatorze, ale różnej intensywności są różne, jest zdefiniowane w implementacji. Jeśli jest to dozwolone, funkcja CURVEAREA może być zdefiniowana dwukrotnie, aby zastąpić zarówno monadyczny CIRCLEAREA, jak i dwójkowy SEGMENTAREA, przy czym funkcja monadyczna lub dwójkowa jest wybierana przez kontekst, w którym się do niej odwołuje.
Niestandardowe funkcje dwuczłonowe mogą być zwykle stosowane do parametrów z tymi samymi konwencjami, co funkcje wbudowane, tj. tablice powinny albo mieć taką samą liczbę elementów, albo jedna z nich powinna mieć pojedynczy element, który jest rozszerzany. Są od tego wyjątki, na przykład funkcja przeliczania waluty brytyjskiej z wartością przed przecinkiem na dolary oczekiwałaby przyjęcia parametru z dokładnie trzema elementami reprezentującymi funty, szylingi i pensy.
Wewnątrz programu lub funkcji niestandardowej sterowanie może być warunkowo przekazane do instrukcji identyfikowanej przez numer wiersza lub jawną etykietę; jeśli celem jest 0 (zero), kończy program lub powraca do wywołującego funkcję. Najpopularniejsza forma wykorzystuje funkcję kompresji APL, tak jak w szablonie (warunku)/celu, która powoduje ocenę warunku na 0 (fałsz) lub 1 (prawda), a następnie użycie tego do zamaskowania celu (jeśli warunek jest false jest ignorowany, jeśli true jest pozostawiony sam, więc kontrola jest przekazywana).
Stąd funkcja SEGMENTAREA może zostać zmodyfikowana, aby przerwać (tuż poniżej), zwracając zero, jeśli parametry (DEGREES i RADIUS poniżej) mają inny znak:
∇ AREA←DEGREES SEGMENTAREA RADIUS ; FRACTION ; CA ; SIGN ⍝ local variables denoted by semicolon(;)
FRACTION←DEGREES÷360
CA←CIRCLEAREA RADIUS ⍝ this APL code statement calls user function CIRCLEAREA, defined up above.
SIGN←(×DEGREES)≠×RADIUS ⍝ << APL logic TEST/determine whether DEGREES and RADIUS do NOT (≠ used) have same SIGN 1-yes different(≠), 0-no(same sign)
AREA←0 ⍝ default value of AREA set = zero
→SIGN/0 ⍝ branching(here, exiting) occurs when SIGN=1 while SIGN=0 does NOT branch to 0. Branching to 0 exits function.
AREA←FRACTION×CA
∇
Powyższa funkcja SEGMENTAREA działa zgodnie z oczekiwaniami, jeśli parametry są skalarami lub tablicami jednoelementowymi , ale nie, jeśli są tablicami wieloelementowymi, ponieważ warunek jest oparty na pojedynczym elemencie tablicy SIGN - z drugiej strony użytkownik funkcja może zostać zmodyfikowana, aby poprawnie obsługiwać argumenty zwektoryzowane. Operacja może czasami być nieprzewidywalna, ponieważ APL definiuje, że komputery z możliwościami przetwarzania wektorów powinny być zrównoleglone i mogą zmieniać kolejność operacji na tablicach tak dalece, jak to możliwe - w ten sposób testuj i debuguj funkcje użytkownika, szczególnie jeśli będą używane z argumentami wektorowymi lub nawet macierzowymi. Wpływa to nie tylko na jawne zastosowanie funkcji niestandardowej do tablic, ale także na jej użycie wszędzie tam, gdzie można rozsądnie użyć funkcji dwuczłonowej, na przykład przy generowaniu tabeli wyników:
90 180 270 ¯90 ∘.SEGMENTAREA 1 ¯2 4
0 0 0
0 0 0
0 0 0
0 0 0
Sposobem bardziej zwięzłym, a czasem lepszym - formułowanie funkcji jest unikanie jawnych transferów sterowania, zamiast używania wyrażeń, które obliczają poprawnie we wszystkich lub oczekiwanych warunkach. Czasami poprawne jest pozwolenie funkcji na niepowodzenie, gdy jeden lub oba argumenty wejściowe są niepoprawne - właśnie po to, aby użytkownik wiedział, że jeden lub oba użyte argumenty są niepoprawne. Poniższe jest bardziej zwięzłe niż powyższa funkcja SEGMENTAREA. Poniższe, co ważne, poprawnie obsługuje argumenty zwektoryzowane:
∇ AREA←DEGREES SEGMENTAREA RADIUS ; FRACTION ; CA ; SIGN
FRACTION←DEGREES÷360
CA←CIRCLEAREA RADIUS
SIGN←(×DEGREES)≠×RADIUS
AREA←FRACTION×CA×~SIGN ⍝ this APL statement is more complex, as a one-liner - but it solves vectorized arguments: a tradeoff - complexity vs. branching
∇
90 180 270 ¯90 ∘.SEGMENTAREA 1 ¯2 4
0.785398163 0 12.5663706
1.57079633 0 25.1327412
2.35619449 0 37.6991118
0 ¯3.14159265 0
Unikanie wyraźnych transferów kontroli, zwanych również rozgałęzieniami, jeśli nie jest sprawdzane lub dokładnie kontrolowane - może promować stosowanie nadmiernie skomplikowanych pojedynczych linijek , naprawdę „niezrozumianych i złożonych idiomów” oraz stylu „tylko do zapisu”, który niewiele zrobił, aby przyciągnąć APL do wpływowych komentatorów, takich jak Edsger Dijkstra . I odwrotnie, idiomy APL mogą być zabawne, pouczające i przydatne - jeśli są używane z pomocnymi komentarzami ⍝ , na przykład zawierającymi źródło i zamierzone znaczenie i funkcję idiomu(ów). Oto lista idiomy APL , wykonania lista tutaj IBM APL2 idiomy i fiński APL idiom biblioteka tutaj .
Różne
| Nazwy) | Symbol | Przykład | Znaczenie (na przykład) | Punkt kodu Unicode |
|---|---|---|---|---|
| Wysoki minus | Ż |
¯3
|
Oznacza liczbę ujemną | U + 00AF Ż |
| Lampa, komentarz | ⍝ |
⍝This is a comment
|
Wszystko na prawo od ⍝ oznacza komentarz | U + 235D |
| Strzałka w prawo, gałąź, Idź do | → |
→This_Label
|
→This_Label wysyła wykonanie APL do This_Label: | U+2192 → |
| Przypisz, strzałka w lewo, ustaw na | ← |
B←A
|
B←A ustawia wartości i kształt B, aby dopasować A | U + 2190 ← |
Większość implementacji APL obsługuje wiele zmiennych systemowych i funkcji, zwykle poprzedzonych znakiem ⎕ (quad) i lub ")" ( hook = close parenthesis). Szczególnie ważna i szeroko zaimplementowana jest zmienna ⎕IO ( Index Origin ), ponieważ podczas gdy oryginalna IBM APL opierała swoje tablice na 1, niektóre nowsze warianty opierają je na zero:
| Sesja użytkownika z interpreterem APL | Opis |
|---|---|
X←⍳12
X
1 2 3 4 5 6 7 8 9 10 11 12
⎕IO
1
X[1]
1
|
X set = do wektora 12 kolejnych liczb całkowitych. Początkowy początek indeksu ⎕IO wartość = 1 . Zatem pierwsza pozycja w wektorze X lub X[1] = 1 na wektor wartości jota { 1 2 3 4 5 ...}. |
⎕IO←0
X[1]
2
X[0]
1
|
Początek indeksu ⎕IO zmienił się teraz na 0. Zatem „pierwsza pozycja indeksu” w wektorze X zmienia się z 1 na 0. W konsekwencji X[1] następnie odwołuje się lub wskazuje na 2 z {1 2 3 4 5 ...} i X[0] odwołuje się teraz do 1 . |
⎕WA
41226371072
|
Quad WA lub ⎕WA , kolejna dynamiczna zmienna systemowa , pokazuje, ile Obszaru Roboczego pozostaje niewykorzystane lub 41 226 megabajtów lub około 41 gigabajtów nieużywanego dodatkowego, całkowitego wolnego obszaru roboczego dostępnego dla obszaru roboczego APL i programu do przetwarzania. Jeśli ta liczba spadnie lub zbliży się do zera — komputer może potrzebować więcej pamięci o dostępie swobodnym (RAM), miejsca na dysku twardym lub kombinacji tych dwóch elementów, aby zwiększyć pamięć wirtualną . |
)VARS
X
|
)VARS funkcja systemowa w APL, )VARS pokazuje nazwy zmiennych użytkownika istniejących w bieżącym obszarze roboczym. |
Istnieją również funkcje systemu dostępne dla użytkowników do zapisywania bieżącego obszaru roboczego np ) Zapisz i kończące środowiska APL, np ) OFF - niekiedy zwane hak komendy lub funkcji ze względu na korzystanie z czołowego prawego nawiasu lub haku. Istnieje pewna standaryzacja tych funkcji quad i hook.
Czcionki
Płaszczyzna podstawowa Unicode Basic Multilingual Plane zawiera symbole APL w bloku Miscellaneous Technical , które w ten sposób są zwykle dokładnie renderowane z większych czcionek Unicode zainstalowanych w większości nowoczesnych systemów operacyjnych. Te czcionki są rzadko projektowane przez typografów zaznajomionych z glifami APL. Tak więc, chociaż dokładne, glify mogą wyglądać nieznajomie dla programistów APL lub być trudne do odróżnienia od siebie.
Niektóre czcionki Unicode zostały zaprojektowane tak, aby dobrze wyświetlać APL: APLX Upright, APL385 Unicode i SimPL.
Przed Unicode, interpretery APL były dostarczane z czcionkami, w których znaki APL były mapowane na rzadziej używane pozycje w zestawach znaków ASCII, zwykle w górnych 128 punktach kodowych. Te odwzorowania (i ich narodowe odmiany) były czasami unikalne dla każdego interpretera APL, co powodowało wyświetlanie programów APL w sieci, w plikach tekstowych i podręcznikach - często problematyczne.
Funkcja klawiatury APL2 do mapowania symboli
Zwróć uwagę na klawisz włączania / wyłączania APL - klawisz od góry do prawej, tuż poniżej. Należy również zauważyć, że klawiatura miała około 55 unikalnych (68 wymienionych w tabelach powyżej, w tym symbole porównawcze, ale kilka symboli pojawia się zarówno w tabelach monadycznych, jak i diadycznych) Klawisze symboli APL (55 funkcji APL (operatorów) są wymienione w podręczniku IBM 5110 APL Reference Manual), dlatego z użyciem klawiszy alt, shift i ctrl - teoretycznie pozwoliłoby to maksymalnie na jakieś 59 (klawisze) *4 (przy wciśnięciu 2 klawiszy) *3 (przy wciśnięciu tri-klawiszy np. ctrl-alt-del) lub jakieś 472 różne maksymalne kombinacje klawiszy, zbliżając się do maks. 512 znaków EBCDIC (256 znaków razy 2 kody dla każdej kombinacji klawiszy). Ponownie, teoretycznie klawiatura przedstawiona poniżej pozwoliłaby na aktywne używanie około 472 różnych symboli/funkcji APL. W praktyce wczesne wersje używały tylko czegoś mniej więcej równoważnego 55 specjalnym symbolom APL (z wyłączeniem liter, cyfr, znaków interpunkcyjnych itp.). Tak więc wczesna APL wykorzystywała wtedy tylko około 11% (55/472) ówczesnego potencjału wykorzystania języka symbolicznego, w oparciu o limity klawiszy klawiatury #, ponownie z wyłączeniem cyfr, liter, interpunkcji itp. W innym sensie symbole klawiatury wykorzystanie było bliższe 100%, bardzo wydajne, ponieważ EBCDIC zezwalał tylko na 256 odrębnych znaków, a ASCII tylko na 128.
Rozwiazywac zagadki
APL okazał się niezwykle przydatny w rozwiązywaniu zagadek matematycznych, z których kilka opisano poniżej.
Trójkąt Pascala
Weźmy trójkąt Pascala , który jest trójkątną tablicą liczb, w której te na końcach rzędów to 1 , a każda z pozostałych liczb jest sumą najbliższych dwóch liczb w rzędzie tuż nad nim (wierzchołek 1 jest na szczyt). Poniżej znajduje się jednowierszowa funkcja APL, która wizualnie przedstawia trójkąt Pascala:
Pascal←{0~¨⍨a⌽⊃⌽∊¨0,¨¨a∘!¨a←⌽⍳⍵} ⍝ Create one-line user function called Pascal
Pascal 7 ⍝ Run function Pascal for seven rows and show the results below:
1
1 2
1 3 3
1 4 6 4
1 5 10 10 5
1 6 15 20 15 6
1 7 21 35 35 21 7
Liczby pierwsze, kontra dowód przez czynniki
Określ liczbę liczb pierwszych ( liczba pierwsza # jest liczbą naturalną większą od 1, która nie ma dzielników dodatnich innych niż 1 i sama w sobie) aż do pewnej liczby N. Ken Iverson otrzymuje następujące jednowierszowe rozwiązanie APL:
⎕CR 'PrimeNumbers' ⍝ Show APL user-function PrimeNumbers
Primes←PrimeNumbers N ⍝ Function takes one right arg N (e.g., show prime numbers for 1 ... int N)
Primes←(2=+⌿0=(⍳N)∘.|⍳N)/⍳N ⍝ The Ken Iverson one-liner
PrimeNumbers 100 ⍝ Show all prime numbers from 1 to 100
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
⍴PrimeNumbers 100
25 ⍝ There are twenty-five prime numbers in the range up to 100.
Często potrzebne jest badanie odwrotności lub przeciwieństwa rozwiązania matematycznego ( czynniki całkowite liczby ): Udowodnij dla podzbioru liczb od 1 do 15, że są one inne niż pierwsze , wymieniając ich czynniki rozkładu . Jakie są ich czynniki niejednoznaczne (podzielne przez #, z wyjątkiem 1)?
⎕CR 'ProveNonPrime'
Z←ProveNonPrime R
⍝Show all factors of an integer R - except 1 and the number itself,
⍝ i.e., prove Non-Prime. String 'prime' is returned for a Prime integer.
Z←(0=(⍳R)|R)/⍳R ⍝ Determine all factors for integer R, store into Z
Z←(~(Z∊1,R))/Z ⍝ Delete 1 and the number as factors for the number from Z.
→(0=⍴Z)/ProveNonPrimeIsPrime ⍝ If result has zero shape, it has no other factors and is therefore prime
Z←R,(⊂" factors(except 1) "),(⊂Z),⎕TCNL ⍝ Show the number R, its factors(except 1,itself), and a new line char
→0 ⍝ Done with function if non-prime
ProveNonPrimeIsPrime: Z←R,(⊂" prime"),⎕TCNL ⍝ function branches here if number was prime
ProveNonPrime ¨⍳15 ⍝ Prove non primes for each(¨) of the integers from 1 through 15 (iota 15)
1 prime
2 prime
3 prime
4 factors(except 1) 2
5 prime
6 factors(except 1) 2 3
7 prime
8 factors(except 1) 2 4
9 factors(except 1) 3
10 factors(except 1) 2 5
11 prime
12 factors(except 1) 2 3 4 6
13 prime
14 factors(except 1) 2 7
15 factors(except 1) 3 5
ciąg Fibonacciego
Wygeneruj ciąg liczb Fibonacciego , gdzie każda kolejna liczba w ciągu jest sumą dwóch poprzednich:
⎕CR 'Fibonacci' ⍝ Display function Fibonacci
FibonacciNum←Fibonacci Nth;IOwas ⍝ Funct header, funct name=Fibonacci, monadic funct with 1 right hand arg Nth;local var IOwas, and a returned num.
⍝Generate a Fibonacci sequenced number where Nth is the position # of the Fibonacci number in the sequence. << function description
IOwas←⎕IO ⋄ ⎕IO←0 ⋄ FibonacciNum←↑0 1↓↑+.×/Nth/⊂2 2⍴1 1 1 0 ⋄ ⎕IO←IOwas ⍝ In order for this function to work correctly ⎕IO must be set to zero.
Fibonacci¨⍳14 ⍝ This APL statement says: Generate the Fibonacci sequence over each(¨) integer number(iota or ⍳) for the integers 1..14.
0 1 1 2 3 5 8 13 21 34 55 89 144 233 ⍝ Generated sequence, i.e., the Fibonacci sequence of numbers generated by APL's interpreter.
Dalsza lektura
- Poliwka, Raymond P.; Pakin, Sandra (1975). APL: język i jego użycie . Prentice-Hall. Numer ISBN 978-0-13-038885-8.
- Reiter, Clifford A.; Jones, William R. (1990). APL z matematycznym akcentem (1 wyd.). Taylora i Francisa. Numer ISBN 978-0534128647.
- Thompson, Norman D.; Poliwka, Raymond P. (2013). APL2 in Depth (Springer Series w statystykach) ( Miękka okładka ) (Przedruk oryginału 1st ed.). Skoczek. Numer ISBN 978-0387942131.
- Gilmana, Leonarda; Róża, Allen J. (1976). APL: Interaktywne podejście (oprawa miękka) (3rd ed.). Numer ISBN 978-0471093046.
Zobacz też
- Różne techniczne – blok Unicode, w tym klucze APL
- APL (strona kodowa) § Układ klawiatury - Bardziej nowoczesne informacje o układzie klawiatury APL
Bibliografia
Linki zewnętrzne
- Odniesienie do znaku APL: Strona 1 , Strona 2 , Strona 3 , Strona 4
- Strona czcionek Brytyjskiego Stowarzyszenia APL
- Strona kodowa IBM 293 aka strona kodowa APL na komputerach mainframe
- Ogólne informacje o znakach APL na wiki APL
- rozszerzenie APL i jego klawiatura-symbole-operatory.
- Lee, Xah. „Jak utworzyć układ klawiatury APL lub symboli matematycznych” . Źródło 13 stycznia 2015 .
Ogólne samouczki online
- Praktyczne wprowadzenie do APL 1 i APL 2 autorstwa Graeme Donalda Robertsona
- APL na komputery PC, serwery i tablety — NARS w pełni funkcjonalny, bez ograniczeń, do bezpłatnego pobrania APL/2 z zagnieżdżonymi macierzami firmy Sudley Place Software
- Darmowy interpreter GNU APL do pobrania dla APL autorstwa Jürgena Sauermanna
- Samouczki YouTube APL przesłane przez Jimin Park, 8 filmów instruktażowych dla początkujących i dla początkujących.
- Lista skompilowanych samouczków SIGAPL
- Naucz się APL: samouczek APL autorstwa MicroAPL
Zasady składni
- Gra życia Conwaya w APL, na YouTube
- Iverson, Kenneth E. (1983). "Składnia i semantyka APL" . ACM SIGAPL APL Cytat Quad . 13 (3): 223–231. doi : 10.1145/800062.801221 . Numer ISBN 978-0897910958.
- Gffer, M. (1989). „Przyszła APL: Przykłady i problemy” . ACM SIGAPL APL Cytat Quad . 19 (4): 158–163. doi : 10.1145/75144.75166 . Numer ISBN 978-0897913270.