Dodecagram - Dodecagram

Zwykły dodecagram
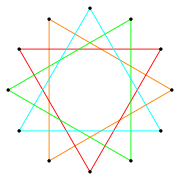
	Zwykły dodekagram
Rodzaj	Regularny wielokąt gwiazdy
Krawędzie i wierzchołki	12
Symbol Schläfli	{12/5} ; t {6/5}
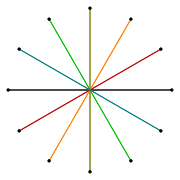
Diagram Coxetera	;
Grupa symetrii	Dwuścienny (D 12 )
Kąt wewnętrzny ( stopnie )	30 °
Podwójny wielokąt	samego siebie
Nieruchomości	gwiazda , cykliczna , równoboczna , izogonalna , izotoksyczna

Dodecagram jest wielokątem gwiazdki lub związek z 12 wierzchołków . Istnieje jeden regularny wielokąt dodecagram {12/5}, którego liczba zwrotna wynosi 5. Istnieją również 4 regularne związki {12/2}, {12/3} {12/4} i {12/6}

Nazwa „dodecagram” łączy przedrostek liczbowy dodeca- z greckim przyrostkiem -gram . W -gram wyprowadza sufiks γραμμῆς ( gramy ), co oznacza linię.

Zwykły dodecagram

Istnieje jedna regularna forma: {12/5}, zawierająca 12 wierzchołków, z liczbą zwrotną równą 5. Regularny dodekagram ma taki sam układ wierzchołków jak regularny dwunastokąt , który można uznać za {12/1}.

Dodekagramy jako regularne związki

Istnieją cztery zwykłe figurki gwiazd dodecagramu : {12/2} = 2 {6}, {12/3} = 3 {4}, {12/4} = 4 {3} i {12/6} = 6 { 2}. Pierwszy to związek dwóch sześciokątów , drugi to związek trzech kwadratów , trzeci to związek czterech trójkątów , a czwarty to związek sześciu prostopadłościennych digonów . Ostatnie dwa można uznać za związki dwóch heksagramów złożonych, a ostatnie jako trzy tetragramy złożone.

2 {6}
3 {4}
4 {3}
6 {2}

Dodekagramy jako figury izotoksyczne

Isotoxal wielokąt ma dwa wierzchołki jeden typ krawędzi w obrębie tej klasy symetrii. Istnieje 5 izotoksalowych gwiazd dodekagramowych z pewnym stopniem swobody kątów, które naprzemiennie zawierają wierzchołki na dwóch promieniach, jedna prosta, 3 związki i 1 gwiazda jednoroczna.

Dodekagramy izotoksalowe
Rodzaj	Prosty	Związki			Gwiazda
Gęstość	1	2	3	4	5
Wizerunek	{(6) _α }	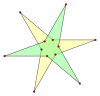2 {3 _α }	3 {2 _α }	2 {(3/2) _α }	{(6/5) _α }

Dodekagramy jako figury izogonalne

Zwykły dodekagram może być postrzegany jako prawie ścięty sześciokąt, t {6/5} = {12/5}. Inne odmiany izogonalne ( przechodnie przez wierzchołki ) z równo rozmieszczonymi wierzchołkami można skonstruować z dwoma długościami krawędzi.

t {6}			t {6/5} = {12/5}

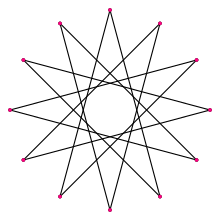
Pełny wykres

Nałożenie na siebie wszystkich dwunastokątów i dodekagramów - w tym zdegenerowanego związku sześciu digonów (odcinków linii), {12/6} - daje pełny wykres K ₁₂ .

K ₁₂
	czarny: dwanaście punktów narożnych (węzłów) czerwony: {12} zwykły dwunastokąt zielony: {12/2} = 2 {6} dwa sześciokąty niebieski: {12/3} = 3 {4} trzy kwadraty cyjan: {12/4} = 4 {3} cztery trójkąty magenta : {12/5} zwykły dodecagram żółty: {12/6} = 6 {2} sześć cyfr

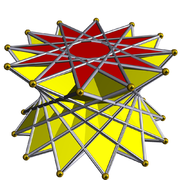
Regularne dodekagramy w wielościanach

Dodekagramy można również włączać do jednorodnych wielościanów . Poniżej znajdują się trzy jednorodne wielościany pryzmatyczne zawierające regularne dodekagramy (nie ma innych jednorodnych wielościanów zawierających dodekagram).

Dodekagramy można również włączyć do teselacji gwiazd na płaszczyźnie euklidesowej.

Symbolika dodecagramu

Dwunastoramienna gwiazda jest charakterystycznym elementem starożytnych wietnamskich bębnów Dong Son

Dodecagramy lub dwunastoramienne gwiazdy zostały użyte jako symbole następujących elementów:

Zobacz też

Bibliografia

Weisstein, Eric W. „Dodecagram” . MathWorld .
Grünbaum, B. i GC Shephard; Tilings and Patterns , Nowy Jork: WH Freeman & Co., (1987), ISBN 0-7167-1193-1 .
Grünbaum, B .; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes… etc. (Toronto 1993) , red. T. Bisztriczky i in., Kluwer Academic (1994) str. 43–70.
John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Rozdział 26. str. 404: Regular star-polytopes Dimension 2)

Languages

In other projects