Dwunastokąt - Dodecagon

Zwykły dwunastokąt
	Zwykły dwunastokąt
Rodzaj	Regularny wielokąt
Krawędzie i wierzchołki	12
Symbol Schläfli	{12}, t {6}, tt {3}
Diagram Coxetera	;
Grupa symetrii	Dwuścienny (D 12 ), rząd 2 × 12
Kąt wewnętrzny ( stopnie )	150 °
Podwójny wielokąt	Samego siebie
Nieruchomości	Wypukły , cykliczny , równoboczny , izogonalny , izotoksyczny

W geometrii , o dwunastokąt lub 12-gon jest dowolny dwanaście jednostronne wielokąt .

Zwykły dwunastokąt

Regularne dwunastokąt to postać o bokach jednakowej długości i wewnętrznymi kątami o tej samej wielkości. Ma dwanaście linii odblaskowej symetrii i symetrii obrotowej rzędu 12. Dwunastokąt regularny jest reprezentowany przez symbol Schläfli {12} i może być zbudowany jako ścięty sześciokąt , t {6} lub podwójnie ścięty trójkąt , tt {3 }. Kąt wewnętrzny w każdym wierzchołku dwunastokąta foremnego wynosi 150 °.

Powierzchnia

Obszar regularnego dwunastokąta o długości boku a jest dana przez:

{\ Displaystyle {\ rozpocząć {wyrównane} A & = 3 \ cot \ lewo ({\ Frac {\ pi} {12}} \ prawej) a ^ {2} = 3 \ lewo (2 + {\ sqrt {3}}) \ right) a ^ {2} \\ & \ simeq 11.19615242 \, a ^ {2} \ end {aligned}}}

A jeśli chodzi o apotem r (patrz również wpisany rysunek ), pole to:

{\ Displaystyle {\ rozpocząć {wyrównane} A & = 12 \ tan \ lewo ({\ Frac {\ pi} {12}} \ prawej) r ^ {2} = 12 \ lewo (2 - {\ sqrt {3}}) \ right) r ^ {2} \\ & \ simeq 3.2153903 \, r ^ {2} \ end {aligned}}}

Pod względem promienia promienia R obszar ten wynosi:

{\ Displaystyle A = 6 \ sin \ lewo ({\ Frac {\ pi} {6}} \ prawej) R ^ {2} = 3R ^ {2}}

Rozpiętość S dwunastokąta jest odległością między dwoma równoległymi bokami i jest równa dwukrotności apotemu. Prosty wzór na powierzchnię (podaną długość i rozpiętość boku) to:

{\ displaystyle A = 3aS}

Można to zweryfikować za pomocą zależności trygonometrycznej:

{\ Displaystyle S = a (1 + 2 \ cos {30 ^ {\ circ}} + 2 \ cos {60 ^ {\ circ}})}

Obwód

Obwód regularnej dwunastokąta pod względem circumradius jest:

{\ Displaystyle {\ rozpocząć {wyrównane} p & = 24R \ tan \ lewo ({\ Frac {\ pi} {12}} \ prawej) = 12R {\ sqrt {2 - {\ sqrt {3}}}} \\ & \ simeq 6.21165708246 \, R \ end {aligned}}}

Obwód w kategoriach apotemów to:

{\ Displaystyle {\ rozpocząć {wyrównane} p & = 24r \ tan \ lewo ({\ Frac {\ pi} {12}} \ prawej) = 24r (2 - {\ sqrt {3}}) \\ & \ simeq 6,43078061835 \, r \ end {aligned}}}

Współczynnik ten jest dwukrotnością współczynnika znalezionego w równaniu apotemu dla pola powierzchni.

Konstrukcja dwunastokąta

Ponieważ 12 = 2 ² × 3, regularny dwunastokąt można skonstruować za pomocą konstrukcji kompasu i prostej :

Budowa regularnego dwunastokąta w danym okręgu opisanym

Budowa dwunastokąta foremnego
na zadanej długości boku, animacja. (Konstrukcja jest bardzo podobna do konstrukcji ośmiokąta przy danej długości boku ).

Sekcja

12-cube	15 rozwarstwienie rombów	60 rombów rozwarstwiających

Dwunastokąt izotoksalu

Coxeter stwierdza, że każdy zonoedr (2 m- kąt, którego przeciwległe boki są równoległe i równej długości) można podzielić na m ( m -1) / 2 równoległoboki. W szczególności dotyczy to regularnych wielokątów z równomiernie wieloma bokami, w którym to przypadku wszystkie równoległoboki są rombami. Dla zwykłego Dwunastokąt , m = 6 i może być podzielona na 15: 3 pola, 6 o szerokości 30 ° rombów i 6 wąskich 15 ° rombów. Rozkład ten jest oparty na wielokąta Petrie rzucie 6-kostki , 15 z 240 powierzchni. Sekwencja OEIS A006245 definiuje liczbę rozwiązań jako 908, w tym do 12-krotnych obrotów i chiralnych form w odbiciu.

Rozcięcie na 15 rombów
6-cube

Jednym ze sposobów wykorzystania matematycznych bloków wzoru manipulacyjnego jest tworzenie wielu różnych dwunastokątów. Są one związane z rozwarstwieniami rombowymi, z 3 rombami 60 ° połączonymi w sześciokąty, pół-sześciokątne trapezoidy lub podzielonymi na 2 trójkąty równoboczne.

Inne sekcje
Regularny		bloki szyku

Symetria

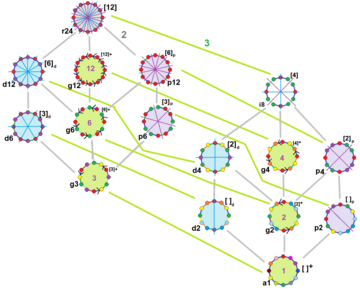
Symetrie dwunastokąta foremnego, jak pokazano z kolorami na krawędziach i wierzchołkach. John Conway określa te niższe symetrie literą, a kolejność symetrii następuje po literze. Daje d (przekątna, diasymetria) z liniami lustrzanymi przechodzącymi przez wierzchołki, p z liniami lustrzanymi przechodzącymi przez krawędzie (prostopadłość, persymetria) i liniami lustrzanymi przechodzącymi przez wierzchołki i krawędzie (izosymetria) oraz g dla rotacji (żyrosymetria). asymetria etykiet a1 . Te niższe symetrie umożliwiają stopnie swobody w definiowaniu nieregularnych dwunastokątów.

Regularne dwunastokąt ma dih ₁₂ symetrii, rząd 24 jest 15 różne podgrupy dwuścienne i cykliczne symetrie. Symetria każdej podgrupy dopuszcza jeden lub więcej stopni swobody dla nieregularnych form. Tylko podgrupa g12 nie ma stopni swobody, ale może być postrzegana jako skierowane krawędzie .

Przykład dwunastokątów na podstawie symetrii
r24
d12	g12	s. 12	i8
d6	g6	p6	d4	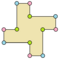g4	p4
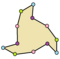g3			d2	g2	p2
a1

Występowanie

Dekarstwo

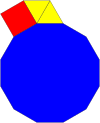
Dwunastokąt foremny może wypełnić wierzchołek płaszczyzny innymi wielokątami regularnymi na 4 sposoby:

3.12.12	4.6.12	3.3.4.12	3.4.3.12

Oto 3 przykłady okresowych przechyleń płaszczyzn, które używają dwunastokątów regularnych, zdefiniowanych przez ich konfigurację wierzchołków :

1-jednolity		2-jednolity
3.12.12	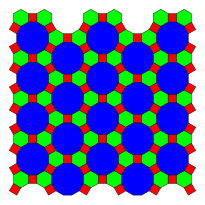4.6.12	3.12.12; 3.4.3.12

Dwunastokąt pochylony

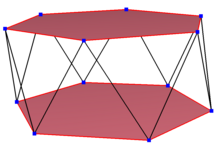
Dwunastokąt o regularnym skosie widziany jako zygzakowate krawędzie sześciokątnego antypryzmatu .

Pochylać dwunastokąt jest wielokąt skośny z 12 wierzchołków i krawędzi, ale nie istniejących na tej samej płaszczyźnie. Ogólnie rzecz biorąc, wnętrze takiego dwunastokąta nie jest zdefiniowane. Skosu zygzakowata dwunastokąt ma przemienne wierzchołki dwóch równoległych płaszczyznach.

Regularne pochylać dwunastokąt jest wierzchołek-przechodnia o równych długościach krawędzi. W 3 wymiarach będzie to dwunastokąt zygzakowaty skośny i można go zobaczyć w wierzchołkach i bocznych krawędziach sześciokątnego antypryzmatu o tej samej symetrii D _5d , [2 ⁺ , 10], rzędu 20. Dodekagramowy antypryzmat , s { 2,24 / 5} i dodecagrammic cross-antiprism , s {2,24 / 7} również mają regularne dwunastokąty ukośne.

Wielokąty Petriego

Dwunastokąt regularny jest wielokątem Petriego dla wielu wielowymiarowych polytopów, widzianym jako rzuty ortogonalne na płaszczyznach Coxetera . Przykładami w 4 wymiarach są: 24-komorowy , 24-komorowy snub , 6-6 duopryzm , 6-6 duopiramid . W 6 wymiarach 6-cube , 6-orthoplex , 2 ₂₁ , 1 ₂₂ . Jest to również wielokąt Petriego dla wielkich 120-ogniwowych i wielogwiazdkowych 120-ogniwowych .

Regularne dwunastokąty skośne w wyższych wymiarach
E ₆		F ₄		2G ₂ (4D)
2 ₂₁	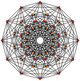1 ₂₂	24 ogniwa	Snub 24-ogniwowy	6-6 duopiramid	6-6 duopryzm
A ₁₁	D ₇		B ₆
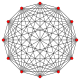11-simplex	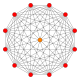(4 ₁₁ )	1 ₄₁	6-ortoplex	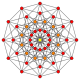6-cube

Powiązane dane

Dodecagram jest 12-stronne wielokąt gwiaździsty, reprezentowany przez symbol {12 / N}. Jest jeden regularny wielokąt gwiezdny : {12/5}, wykorzystujący te same wierzchołki, ale łączący co piąty punkt. Istnieją również trzy związki: {12/2} zmniejsza się do 2 {6} jako dwa sześciokąty , a {12/3} do 3 {4} jako trzy kwadraty , {12/4} do 4 {3 } jako cztery trójkąty, a {12/6} jest zredukowane do 6 {2} jako sześć zdegenerowanych digonów .

Gwiazdy i związki
n	1	2	3	4	5	6
Formularz	Wielokąt	Związki			Wielokąt gwiazdy	Złożony
Wizerunek	{12/1} = {12}	{12/2} lub 2 {6}	{12/3} lub 3 {4}	{12/4} lub 4 {3}	{12/5}	{12/6} lub 6 {2}

Głębsze obcięcia dwunastokąta foremnego i dodekagramów mogą tworzyć izogonalne ( przechodzące przez wierzchołki ) formy pośrednich wielokątów gwiazd o równych odstępach wierzchołków i dwóch długościach krawędzi. Ścięty sześciokąt to dwunastokąt, t {6} = {12}. Prawie ścięty sześciokąt, odwrócony jak {6/5}, to dodekagram: t {6/5} = {12/5}.

Obcięcie sześciokąta przechodnie przez wierzchołki
Quasiregular	Izogonalne		Quasiregular
t {6} = {12}			t {6/5} = {12/5}

Przykłady w użyciu

W literami litery E , H , a x (i I w Egipcjanka czcionką) mają dwunastokątną kontury. Krzyż jest dwunastokąt, podobnie jak logo dla Chevrolet podziału samochodowym.

Kościół Vera Cruz w Segowii

Regularny dwunastokąt jest wyraźnie widoczny w wielu budynkach. Torre del Oro jest dwunastokątną wojskowy strażnica w Sewilli , w południowej Hiszpanii , zbudowany przez dynastii Almohadów . Kościół Vera Cruz z początku XIII wieku w Segowii w Hiszpanii jest dwunastokątny. Innym przykładem jest Porta di Venere (Wenus Gate), w Spello , Włochy , zbudowany w 1 wieku pne posiada dwa dwunastokątną wież, zwanych „Propercjusza wieże”.

Brytyjska trzypensówka z 1942 roku, rewers

Zwykłe dwunastokątne monety obejmują:

Brytyjski kawałek za trzy grosze od 1937 do 1971 roku, kiedy przestał być prawnym środkiem płatniczym.
Brytyjska moneta jednofuntowa , wprowadzona w 2017 r.
Australijska moneta 50 centów
Fidżi 50 centów
Tongan 50-seniti , od 1974 roku
Wyspy Salomona 50 centów
Chorwacka 25 kun
Rumuński 5000 lei , 2001–2005
Pens kanadyjski , 1982–1996
Południowowietnamski 20 đồng , 1968–1975
Zambian 50 ngwee , 1969–1992
Malawian 50 tambala , 1986–1995
Meksykańskie 20 centavos , 1992-2009

Languages

In other projects