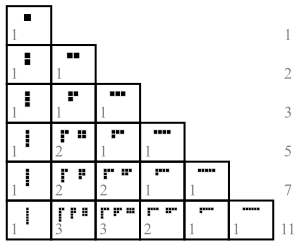Partycja (teoria liczb) - Partition (number theory)

Diagramy Younga związane z podziałami liczb całkowitych dodatnich od 1 do 8. Ułożone są tak, że obrazy pod odbiciem wokół głównej przekątnej kwadratu są podziałami sprzężonymi.

Partycje n z największym dodatkiem k

W teorii liczb i kombinatoryki , A partycja pozytywnej liczby całkowitej n , zwany również partycja liczbą całkowitą , jest sposobem na pisanie n jako suma dodatnich liczb całkowitych. Dwie sumy, które różnią się tylko kolejnością ich sum, są uważane za ten sam podział. (Jeśli kolejność ma znaczenie, suma staje się złożeniem ). Na przykład 4 można podzielić na pięć różnych sposobów:

4

3 + 1

2 + 2

2 + 1 + 1

1 + 1 + 1 + 1

Zależna od kolejności kompozycja 1 + 3 jest tym samym podziałem co 3 + 1, podczas gdy dwie odrębne kompozycje 1 + 2 + 1 i 1 + 1 + 2 reprezentują ten sam podział 2 + 1 + 1.

Suma w partycji nazywana jest również częścią . Liczba partycji n jest podana przez funkcję partycji p ( n ). Zatem p (4) = 5. Notacja λ ⊢ n oznacza, że λ jest podziałem n .

Partycje mogą być wizualizowane graficznie za pomocą diagramów Younga lub diagramów Ferrersa . Występują one w wielu gałęziach matematyki i fizyki , w tym studium wielomianów symetrycznych i do grupy symetrycznej i w grupie teorii reprezentacji w ogóle.

Przykłady

Siedem partycji po 5 to:

• 5
• 4 + 1
• 3 + 2
• 3 + 1 + 1
• 2 + 2 + 1
• 2 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1

W niektórych źródłach podziały traktowane są jako ciąg sum, a nie jako wyrażenie ze znakiem plus. Na przykład, partycja 2 + 2 + 1 może być zamiast tego zapisana jako krotka (2, 2, 1) lub w jeszcze bardziej zwartej formie (2 ² , 1), gdzie indeks górny wskazuje liczbę powtórzeń terminu.

Reprezentacje przegród

Istnieją dwie popularne metody diagramowe do przedstawiania partycji: jako diagramy Ferrersa, nazwane na cześć Normana Macleoda Ferrersa oraz jako diagramy Younga, nazwane na cześć brytyjskiego matematyka Alfreda Younga . Oba mają kilka możliwych konwencji; tutaj używamy notacji angielskiej , z diagramami wyrównanymi w lewym górnym rogu.

Schemat Ferrerów

Podział 6 + 4 + 3 + 1 liczby dodatniej 14 można przedstawić za pomocą następującego diagramu:

14 kół jest ustawionych w 4 rzędach, każdy o wielkości części przegrody. Schematy dla 5 przegród numeru 4 są wymienione poniżej:

4	=	3 + 1	=	2 + 2	=	2 + 1 + 1	=	1 + 1 + 1 + 1

Młody schemat

Alternatywną wizualną reprezentacją partycji liczb całkowitych jest jej diagram Younga (często nazywany również diagramem Ferrersa). Zamiast przedstawiać podział za pomocą kropek, jak na diagramie Ferrersa, diagram Younga używa pudełek lub kwadratów. Zatem diagram Younga dla podziału 5 + 4 + 1 to

podczas gdy diagram Ferrers dla tej samej partycji to

Choć ta pozornie banalna odmiana nie wydaje się warta osobnej wzmianki, diagramy Younga okazują się niezwykle przydatne w badaniu funkcji symetrycznych i teorii reprezentacji grup : wypełniając pola diagramów Younga liczbami (lub czasami bardziej skomplikowanymi obiektami) przestrzegając różnych reguły prowadzą do rodziny obiektów zwanych Young tableaux , a te obrazy mają znaczenie kombinatoryczne i teoretyczne. Jako rodzaj kształtu utworzonego przez połączone ze sobą sąsiednie kwadraty, diagramy Younga są szczególnym rodzajem poliomino .

Funkcja partycji

Używając metody Eulera, aby znaleźć p (40): Linijka ze znakami plus i minus (szare pole) jest przesuwana w dół, a odpowiednie terminy są dodawane lub odejmowane. Pozycje znaków wynikają z różnic naprzemiennych liczb naturalnych (niebieskich) i nieparzystych (pomarańczowych). W pliku SVG najedź kursorem na obraz, aby przesunąć linijkę.

Funkcja podziału jest równa liczbie możliwych podziałów nieujemnej liczby całkowitej . Na przykład, ponieważ całkowita posiada pięć stref , , , , i . Wartości tej funkcji dla to: ${\ Displaystyle p (n)}$${\ Displaystyle n}$${\ Displaystyle p (4) = 5}$${\ Displaystyle 4}$${\ Displaystyle 1+1+1+1}$${\displaystyle 1+1+2}$${\displaystyle 1+3}$${\displaystyle 2+2}$${\ Displaystyle 4}$${\displaystyle n=0,1,2,\kropki}$

1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, 3718, 4565, 5604, ... (sekwencja A000041 w OEIS ).

Funkcja generująca is ${\displaystyle p}$

${\ Displaystyle \ suma _ {n = 0} ^ {\ infty} p (n) q ^ {n} = \ prod _ {j = 1} ^ {\ infty} \ suma _ {i = 0} ^ {\ infty }q^{ji}=\prod _{j=1}^{\infty }(1-q^{j})^{-1}.}$

Żadne wyrażenie w formie zamkniętej dla funkcji podziału nie jest znane, ale ma zarówno rozwinięcia asymptotyczne, które dokładnie ją aproksymują, jak i relacje rekurencyjne, dzięki którym można ją dokładnie obliczyć. Rośnie jako funkcji wykładniczej z pierwiastka kwadratowego jego argumentacji. Liczba odwrotna od jej funkcji tworzącej jest funkcja Eulera ; według twierdzenia Eulera o liczbie pięciokątnej funkcja ta jest przemienną sumą potęg liczb pięciokątnych swojego argumentu.

${\ Displaystyle p (n) = p (n-1) + p (n-2)-p (n-5)-p (n-7) + \ cdots }$

Srinivasa Ramanujan po raz pierwszy odkrył, że funkcja podziału ma nietrywialne wzorce w arytmetyce modularnej , obecnie znanej jako kongruencje Ramanujan . Na przykład, ilekroć reprezentacja dziesiętna kończy się cyfrą 4 lub 9, liczba partycji będzie podzielna przez 5. ${\ Displaystyle n}$${\ Displaystyle n}$

Partycje z ograniczeniami

Zarówno w kombinatoryce, jak iw teorii liczb często badane są rodziny podziałów podlegające różnym ograniczeniom. W tej sekcji omówiono kilka takich ograniczeń.

Przegrody sprzężone i samokoniugujące

Jeśli odwrócimy schemat partycji 6 + 4 + 3 + 1 wzdłuż jej głównej przekątnej, otrzymamy kolejną partycję 14:

	↔
6 + 4 + 3 + 1	=	4 + 3 + 3 + 2 + 1 + 1

Zamieniając wiersze w kolumny, otrzymujemy podział 4 + 3 + 3 + 2 + 1 + 1 liczby 14. Mówi się, że takie podziały są sprzężone ze sobą. W przypadku liczby 4, podzbiory 4 i 1+1+1+1 są parami sprzężonymi, a podzbiory 3+1 i 2+1+1 są sprzężone ze sobą. Szczególnie interesujący jest podział 2 + 2, który sam jest sprzężony. Mówi się, że taki podział jest samokoniugujący .

Twierdzenie : Liczba samosprzężonych partycji jest taka sama jak liczba partycji z odrębnymi częściami nieparzystymi.

Dowód (zarys) : Kluczową obserwacją jest to, że każdą nieparzystą część można „ złożyć ” na środku, tworząc diagram samosprzężający:

↔

Można wtedy uzyskać bijekcję między zbiorem partycji z różnymi częściami nieparzystymi a zbiorem partycji samosprzężonych, co ilustruje następujący przykład:

	↔
9 + 7 + 3	=	5 + 5 + 4 + 3 + 2
Dystans. dziwne		samokoniugat

Części nieparzyste i części odrębne

Wśród 22 partycji liczby 8 jest 6, które zawierają tylko części nieparzyste :

• 7 + 1
• 5 + 3
• 5+1+1+1
• 3 + 3 + 1 + 1
• 3 + 1 + 1 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

Alternatywnie moglibyśmy policzyć partycje, w których żadna liczba nie występuje więcej niż raz. Taka przegroda nazywana jest przegrodą z odrębnymi częściami . Jeśli policzymy podziały 8 z różnymi częściami, otrzymamy również 6:

• 8
• 7 + 1
• 6 + 2
• 5 + 3
• 5 + 2 + 1
• 4 + 3 + 1

To jest właściwość ogólna. Dla każdej liczby dodatniej liczba przegród z częściami nieparzystymi jest równa liczbie przegród o odrębnych częściach, oznaczonych przez q ( n ). Wynik ten został udowodniony przez Leonharda Eulera w 1748 roku, a później został uogólniony jako twierdzenie Glaishera .

Dla każdego typu strefy z ograniczeniami istnieje odpowiednia funkcja dla liczby stref spełniających dane ograniczenie. Ważnym przykładem jest q ( n ). Kilka pierwszych wartości q ( n ) to (zaczynając od q (0)=1):

1, 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, ... (sekwencja A000009 w OEIS ).

Funkcja generująca dla q ( n ) (podziały na odrębne części) jest dana przez

${\ Displaystyle \ suma _ {n = 0} ^ {\ infty} q (n) x ^ {n} = \ prod _ {k = 1} ^ {\ infty} (1 + x ^ {k}) = \ prod _{k=1}^{\infty }{\frac {1}{1-x^{2k-1}}}.}$

Liczba pięciokątny twierdzenie daje powtórzeniu dla q :

q ( k ) = a _k + q ( k − 1) + q ( k − 2) − q ( k − 5) − q ( k − 7) + q ( k − 12) + q ( k − 15) − q ( k − 22) − ...

gdzie a _k jest (-1) ^m jeśli k = 3 m ² - m lub k = 3 m ² + m dla pewnej liczby całkowitej mi wynosi 0 w przeciwnym razie.

Ograniczony rozmiar części lub liczba części

Biorąc koniugaty, liczba p _k ( n ) podziałów n na dokładnie k części jest równa liczbie podziałów n, w których największa część ma rozmiar k . Funkcja p _k ( n ) spełnia rekurencję

p _k ( n ) = p _k ( n − k ) + p _{k −1} ( n − 1)

z wartościami początkowymi p ₀ (0) = 1 i p _k ( n ) = 0 jeśli n ≤ 0 lub k ≤ 0 i n i k nie są oba zerami.

Odzyskuje się funkcję p ( n ) przez

${\ Displaystyle p (n) = \ suma _ {k = 0} ^ {n} p_ {k} (n).}$

Jedną z możliwych funkcji generujących dla takich przegród, przyjmującą k stałych i n zmienną, jest

${\ Displaystyle \ suma _ {n \ geq 0} p_ {k} (n) x ^ {n} = x ^ {k} \ cdot \ prod _ {i = 1} ^ {k} {\ Frac {1} {1-x^{i}}}.}$

Bardziej ogólnie, jeśli T jest zbiorem dodatnich liczb całkowitych, to liczba podzbiorów n , których wszystkie części należą do T , ma funkcję generującą

${\ Displaystyle \ prod _ {t \ w T} (1-x ^ {t}) ^ {-1}.}$

Można to wykorzystać do rozwiązywania problemów związanych z wprowadzaniem zmian (gdzie zestaw T określa dostępne monety). Jako dwa szczególne przypadki, jeden ma to, że liczba partycji n, w których wszystkie części to 1 lub 2 (lub, równoważnie, liczba partycji n na 1 lub 2 części) jest

${\displaystyle \lewo\lpodłoga {\frac {n}{2}}+1\prawo\rpodłoga,}$

a liczba podziałów n, w których wszystkie części to 1, 2 lub 3 (lub, równoważnie, liczba podziałów n na co najwyżej trzy części) jest najbliższą liczbą całkowitą ( n + 3) ² / 12.

Asymptotyki

Asymptotyczne tempo wzrostu przez p ( n ) uzyskuje się

${\ Displaystyle \ log p (n) \ sim C {\ sqrt {n}} {\ tekst {jako}} n \ rightarrow \ infty}$

gdzie . Bardziej precyzyjna formuła asymptotyczna ${\displaystyle C=\pi {\sqrt {\frac {2}{3}}}.}$

${\displaystyle p(n)\sim {\frac {1}{4n{\sqrt {3}}}}\exp \ lewo({\pi {\sqrt {\frac {2n}{3}}}}\ Prawidłowy)}$ jak ${\displaystyle n\rightarrow \infty}$

został po raz pierwszy uzyskany przez GH Hardy'ego i Ramanujana w 1918 roku i niezależnie przez JV Uspensky'ego w 1920 roku. Całkowitą asymptotyczną ekspansję podał w 1937 roku Hans Rademacher .

Jeśli A jest zbiorem liczb naturalnych, niech p _A ( n ) oznacza liczbę podziałów n na elementy A . Jeśli A ma dodatnią gęstość naturalną α, to

${\ Displaystyle \ log p_ {A} (n) \ SIM C {\ sqrt {\ alfa n}}}$

i odwrotnie, jeśli ta asymptotyczna własność zachodzi dla p _A ( n ), to A ma naturalną gęstość α. Wynik ten, wraz ze szkicem dowodu, stwierdził Erdős w 1942 roku.

Jeśli A jest zbiorem skończonym, ta analiza nie ma zastosowania (gęstość zbioru skończonego wynosi zero). Jeśli A ma k elementów, których największym wspólnym dzielnikiem jest 1, to

${\ Displaystyle p_ {A} (n) = \ lewo (\ prod _ {a \ w A} a ^ {-1} \ prawej) \ cdot {\ Frac {n ^ {k-1}} {(k- 1)!}}+O(n^{k-2}).}$

Podziały w prostokącie i współczynniki dwumianowe Gaussa

Można również jednocześnie ograniczyć liczbę i wielkość części. Niech p ( N , M ; n ) oznacza liczbę n podziałów z co najwyżej M częściami, każda o rozmiarze co najwyżej N . Równoważnie są to partycje, których diagram Younga mieści się w prostokącie M × N. Istnieje relacja nawrotu

${\ Displaystyle p (N, M; n) = p (N, M-1; n) + p (N-1, M; nM)}$

uzyskane przez obserwację, że liczy podziały n na dokładnie M części o rozmiarze co najwyżej N , a odjęcie 1 od każdej części takiego podziału daje podział n − M na co najwyżej M części. ${\displaystyle p(N,M;n)-p(N,M-1;n)}$

Gaussa dwumianowego współczynnika określa się jako:

${\ Displaystyle {k + \ ell \ wybrać \ ell} _ {q} = {k + \ ell \ wybrać k} _ {q} = {\ Frac {\ prod _ {j = 1} ^ {k + \ ell} (1 -q^{j})}{\prod _{j=1}^{k}(1-q^{j})\prod _{j=1}^{\ell }(1-q^{j })}}.}$

Gaussa dwumianowego współczynnik odnosi się do funkcji tworzącej z P ( N , M , N ), przy równości

${\ Displaystyle \ suma _ {n = 0} ^ {MN} p (N, M; n) q ^ {n} = {M + N \ wybierz M} _ {q}}.$

Ranga i kwadrat Durfee

Ranking partycji jest największa liczba k taka, że przegroda zawiera co najmniej k części o rozmiarze co najmniej k . Na przykład, podział 4 + 3 + 3 + 2 + 1 + 1 ma rangę 3, ponieważ zawiera 3 części, które są ≥ 3, ale nie zawiera 4 części, które są ≥ 4. Na diagramie Ferrersa lub diagramie Younga podziału rangi r , kwadrat r × r wpisów w lewym górnym rogu jest znany jako kwadrat Durfee :

Kwadrat Durfee ma zastosowanie w kombinatoryce w dowodach różnych tożsamości partycji. Ma też pewne znaczenie praktyczne w postaci indeksu h .

Inna statystyka jest również czasami nazywana rangą podziału (lub rangą Dysona), a mianowicie różnicą podziału na k części z największą częścią . Ta statystyka (niezwiązana z opisaną powyżej) pojawia się w badaniu kongruencji Ramanujan . ${\ Displaystyle \ lambda _ {k}-k}$${\ Displaystyle \ lambda _ {k}}$

Krata Younga

Na partycjach istnieje naturalny porządek cząstkowy wynikający z włączenia diagramów Younga. Ten częściowo uporządkowany zestaw jest znany jako krata Younga . Krata została pierwotnie określono w ramach teorii reprezentacji , jeżeli jest używany do opisania nieredukowalnych reprezentacji z grup Symmetric S _n dla wszystkich n , wraz z ich właściwościami rozgałęzienia, w typowym zera. Otrzymał również znaczące badania ze względu na jego czysto kombinatoryczne właściwości; w szczególności jest to motywujący przykład postawy różnicowej .

Zobacz też

Uwagi

Bibliografia

• Abramowitz, Milton ; Stegun, Irena (1964). Podręcznik funkcji matematycznych z formułami, wykresami i tabelami matematycznymi . Departament Handlu Stanów Zjednoczonych, Krajowe Biuro Standardów. Numer ISBN 0-486-61272-4.
• Andrews, George E. (1976). Teoria zaborów . Wydawnictwo Uniwersytetu Cambridge. Numer ISBN 0-521-63766-X.
• Andrews, George E.; Eriksson, Kimmo (2004). Partycje całkowite . Wydawnictwo Uniwersytetu Cambridge. Numer ISBN 0-521-60090-1.
• Apostol, Tom M. (1990) (1976). Funkcje modularne i szereg Dirichleta w teorii liczb . Teksty magisterskie z matematyki . 41 (wyd. 2). Nowy Jork itd.: Springer-Verlag . Numer ISBN 0-387-97127-0. Zbl  0697.10023 . (Patrz rozdział 5 dla nowoczesnego pedagogicznego wprowadzenia do formuły Rademachera) .
• Bona, Miklós (2002). Spacer po kombinatoryce: wprowadzenie do wyliczania i teorii grafów . Światowe Wydawnictwo Naukowe. Numer ISBN 981-02-4900-4. (elementarne wprowadzenie do tematu partycji całkowitych, w tym omówienie grafów Ferrersa)
• Hardy, GH ; Wright, EM (2008) [1938]. Wprowadzenie do teorii liczb . Poprawione przez DR Heath-Browna i JH Silvermana . Przedmowa Andrew Wilesa . (wyd. 6). Oksford: Oxford University Press . Numer ISBN 978-0-19-921986-5. MR  2445243 . Zbl  1159.11001 .
• Lehmer, DH (1939). „Na reszcie i zbieżności szeregu dla funkcji podziału” . Przeł. Amer. Matematyka. Soc . 46 : 362-373. doi : 10.1090/S0002-9947-1939-0000410-9 . MR  0000410 . Zbl  0022.20401 .Zawiera główną formułę (bez pochodnych), resztę i starszą formę dla A _k ( n ).)
• Gupta, Hansraj; Gwyther, CE; Miller, JCP (1962). Królewskie Towarzystwo Matematyczne. Tabele . Tom 4, Tablice partycji. |volume=ma dodatkowy tekst ( pomoc ) (Ma tekst, prawie kompletną bibliografię, ale oni (i Abramowitz) pominęli formułę Selberga dla A _k ( n ), która jest w Whiteman.)
• Macdonald, Ian G. (1979). Funkcje symetryczne i wielomiany Halla . Oksfordzkie Monografie Matematyczne. Wydawnictwo Uniwersytetu Oksfordzkiego . Numer ISBN 0-19-853530-9. Zbl  0487.20007 . (Patrz sekcja I.1)
• Nathansona, MB (2000). Metody elementarne w teorii liczb . Teksty magisterskie z matematyki. 195 . Springer-Verlag . Numer ISBN 0-387-98912-9. Zbl  0953.11002 .
• Rademacher, Hans (1974). Zebrane dokumenty Hansa Rademachera . v II . MIT Naciśnij. s. 100–07, 108–22, 460–75.
• Sautoy, Marcus Du. (2003). Muzyka Najwyższych . Nowy Jork: wieloletnie HarperCollins.
• Stanley, Richard P. (1999). Kombinatoryka enumeracyjna . Tomy 1 i 2. Cambridge University Press. Numer ISBN 0-521-56069-1. |volume=ma dodatkowy tekst ( pomoc )
• Whiteman, AL (1956). „Suma związana z szeregiem dla funkcji podziału” . Pacific Journal of Mathematics . 6 (1): 159–176. doi : 10.2140/pjm.1956.6.159 . Zbl  0071.04004 . (Zapewnia wzór Selberga. Starsza forma jest skończoną ekspansją Fouriera Selberga.)

Zewnętrzne linki

• "Partition" , Encyklopedia Matematyki , EMS Press , 2001 [1994]
• Kalkulator partycji i kompozycji
• Weisstein, Eric W. „Podział” . MatematykaŚwiat .
• Wilf, Herbert S. Lectures on Integer Partitions (PDF) , zarchiwizowane (PDF) z oryginału dnia 2021-02-24 , pobrane 2021-02-28
• Liczenie z partycjami z tabelami odniesienia do On-Line Encyclopedia of Integer Sequences
• Wpis partycji całkowitych w bazie danych FindStat
• Integer::Partition Perl moduł z CPAN
• Szybkie algorytmy do generowania partycji liczb całkowitych
• Generowanie wszystkich partycji: porównanie dwóch kodowań
• Grime, James (28 kwietnia 2016). „Partycje - Numberphile” (wideo) . Brady Haran . Pobrano 5 maja 2016 .