Prosta Simsona LN (czerwona) trójkąta ABC względem punktu P na okręgu opisanym

W geometrii , mając trójkąt ABC i punkt P na jego okręgu opisanym , trzy najbliższe punkty P na liniach AB , AC i BC są współliniowe . Linia przechodząca przez te punkty to linia Simsona od P , nazwana na cześć Roberta Simsona . Koncepcja została jednak po raz pierwszy opublikowana przez Williama Wallace'a w 1799 roku.

Odwrotne jest również prawdziwe; jeśli trzy najbliższe punkty P na trzech liniach są współliniowe i żadna z nich nie jest równoległa, to P leży na okręgu opisanym w trójkącie utworzonym przez te trzy linie. Albo innymi słowy, linia Simson trójkąta ABC i punkt P jest tylko trójkąt pedał z ABC i P , która przerodziła się w linii prostej, a ten warunek ogranicza locus of P prześledzić okrąg opisany na trójkącie ABC .

Równanie

Umieszczając trójkąt na płaszczyźnie zespolonej, niech trójkąt ABC z jednostkowym okręgiem opisanym ma wierzchołki, których położenie ma złożone współrzędne a , b , c , a P o zespolonych współrzędnych p będzie punktem na okręgu opisanym. Linia Simsona to zbiór punktów z spełniających

${\ Displaystyle 2abc {\ bar {z}} -2pz+p ^ {2}+(a+b+c)p-(BC+ca+ab)-{\frac {abc}{p}}=0, }$

gdzie overbar wskazuje złożoną koniugację .

Nieruchomości

Linie Simsona (na czerwono) są styczne do deltoidy Steinera (na niebiesko).

• Linia Simsona wierzchołka trójkąta to wysokość trójkąta opuszczonego z tego wierzchołka, a linia Simsona punktu diametralnie przeciwnego do wierzchołka to bok trójkąta przeciwny do tego wierzchołka.
• Jeśli P i Q są punktami na okręgu opisanym, to kąt między prostymi Simsona linii P i Q jest połową kąta łuku PQ . W szczególności, jeśli punkty są diametralnie przeciwne, ich linie Simsona są prostopadłe i w tym przypadku przecięcie linii leży na dziewięciopunktowym okręgu
• Niech H oznacza ortocentrum trójkąta ABC , prosta Simsona z P przecina odcinek PH w punkcie leżącym na okręgu dziewięciopunktowym.
• Biorąc pod uwagę dwa trójkąty z tym samym okręgiem opisanym, kąt między prostymi Simsona punktu P na okręgu opisanym dla obu trójkątów nie zależy od P .
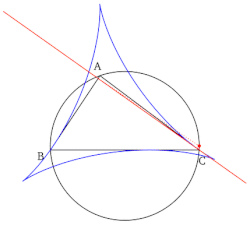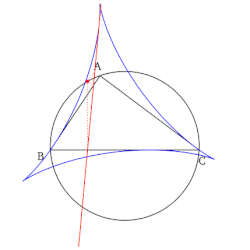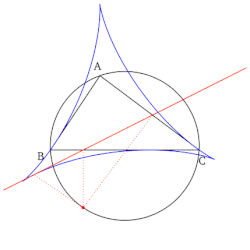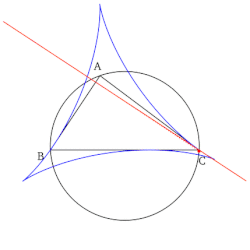
• Zbiór wszystkich linii Simsona, po narysowaniu, tworzy obwiednię w kształcie deltoidu znanego jako deltoid Steinera trójkąta odniesienia.
• Konstrukcja linii Simsona, która pokrywa się z bokiem trójkąta odniesienia (patrz pierwsza właściwość powyżej) daje nietrywialny punkt na tej linii bocznej. Ten punkt jest odbiciem stopy wysokości (opuszczonej na linię boczną) wokół punktu środkowego konstruowanej linii bocznej. Co więcej, ten punkt jest punktem stycznym między bokiem trójkąta odniesienia a jego deltoidem Steinera.
• Czworokąt, który nie jest równoległobokiem, ma jeden i tylko jeden punkt pedałowy, zwany punktem Simsona, względem którego stopy na czworoboku są współliniowe. Punkt Simsona trapezu to punkt przecięcia dwóch nierównoległych boków.
• Żaden wielokąt wypukły z co najmniej 5 bokami nie ma linii Simsona.

Dowód istnienia

Metodą dowodu jest wykazanie, że . jest czworokątem cyklicznym, więc . jest cyklicznym czworokątem ( twierdzenie Thalesa ), więc . Stąd . Teraz jest cykliczny, więc . Dlatego . ${\ Displaystyle \ kąt NMP + \ kąt PML = 180 ^ {\ circ}}$${\ Displaystyle PCB}$${\ Displaystyle \ kąt PBA + \ kąt ACP = \ kąt PBN + \ kąt ACP = 180 ^ {\ okrąg}}$${\displaystyle PMNB}$${\ Displaystyle \ kąt PBN + \ kąt NMP = 180 ^ {\ circ}}$${\ Displaystyle \ kąt NMP = \ kąt ACP}$${\ Displaystyle PLCM}$${\ Displaystyle \ kąt PML = \ kąt PCL = 180 ^ {\ okrąg} - \ kąt ACP}$${\ Displaystyle \ kąt NMP + \ kąt PML = \ kąt ACP + (180 ^ {\ okrąg} - \ kąt ACP) = 180 ^ {\ okrąg}}$

Dowód alternatywny

zielona linia to linia Simsona, niebieskie to prostopadłe.

Jakikolwiek jest punkt Z na sąsiednim rysunku, a + c wynosi 90. Niezależnie od tego, jaki jest punkt Z, c i b będą równe. Dlatego mamy:

a + c = 90

∴ a + b = 90 …(c i b są równe) (1)

Rozważmy teraz miarę kąta: a + 90 + b.

Jeśli pokażemy, że ten kąt wynosi 180, to twierdzenie Simsona jest udowodnione.

Z (1) mamy, a + 90 + b = 180

CO BYŁO DO OKAZANIA

Uogólnienia

Uogólnienie 1

Rzuty Ap, Bp, Cp na BC, CA, AB to trzy punkty współliniowe

• Niech ABC będzie trójkątem, niech prosta ℓ przechodzi przez środek opisany na okręgu O , i niech punkt P leży na okręgu opisanym. Niech AP, BP, CP spotykają się ℓ w odpowiednio A _p , B _p , C _p . Niech ₀ , B ₀ , C ₀ rzutami z A _P , B, _P , C _P na BC, CA, AB , odpowiednio. Wtedy A ₀ , B ₀ , C ₀ są współliniowe. Co więcej, nowa linia przechodzi przez środek PH , gdzie H jest ortocentrum Δ ABC . Jeśli ℓ przechodzi przez P , linia pokrywa się z linią Simsona.

Projektowa wersja linii Simsona

Uogólnienie 2

• Niech wierzchołki trójkąta ABC leżą na stożku Γ i niech Q, P będą dwoma punktami na płaszczyźnie. Niech PA, PB, PC przecinają stożkową odpowiednio w A ₁ , B ₁ , C ₁ . QA ₁ przecina BC w A ₂ , QB ₁ przecina AC w B ₂ , a QC ₁ przecina AB w C ₂ . Wtedy cztery punkty A ₂ , B ₂ , C ₂ i P są współliniowe, jeśli tylko Q leży na stożku Γ.

Uogólnienie 3

• RF Cyster uogólnił twierdzenie na cykliczne czworokąty w liniach Simsona cyklicznego czworokąta

Zobacz też

• Trójkąt pedałów
• Robert Simson

Bibliografia

Zewnętrzne linki

• Simson Line w cut-the-knot .org
• FM Jackson i Weisstein, Eric W. „Simson Line” . MatematykaŚwiat .
• Uogólnienie twierdzenia Neuberga i linii Simsona-Wallace'a w Dynamic Geometry Sketches , interaktywnym dynamicznym szkicu geometrii.