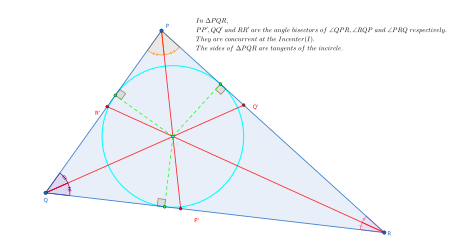
W centrum - Incenter

Punktem przecięcia dwusiecznych kątów trzech kątów trójkąta ABC jest środek (oznaczony przez I). Okrąg (którego środkiem jest I) dotyka każdego boku trójkąta.

W geometrii The incenter trójkąta jest centrum trójkąta , punkt zdefiniowany dla każdego trójkąta w sposób, który jest niezależny od umieszczenia trójkąta lub skali. Środek może być równoważnie zdefiniowany jako punkt, w którym przecinają się wewnętrzne dwusieczne kąta trójkąta, jako punkt równoodległy od boków trójkąta, jako punkt połączenia osi środkowej i najbardziej wewnętrznego punktu transformacji trawiastej trójkąta oraz jako punkt środkowy wpisanego okręgu trójkąta.

Wraz z centroidem , circumcenterem i ortocentrum jest jednym z czterech centrów trójkąta znanych starożytnym Grekom i jedynym, który nie leży w zasadzie na linii Eulera . Jest to pierwszy wymieniony środek X (1), w Clark Kimberling „s Encyclopedia centrów Triangle , a element neutralny na przykład multiplikatywna grupa centrów trójkąta.

W przypadku wielokątów o więcej niż trzech bokach środek istnieje tylko dla wielokątów stycznych - tych, które mają okrąg styczny do każdej strony wielokąta. W tym przypadku środek jest środkiem tego okręgu i jest jednakowo oddalony ze wszystkich stron.

Definicja i konstrukcja

Jest to twierdzenie w geometrii euklidesowej, że trzy wewnętrzne dwusieczne kąta trójkąta spotykają się w jednym punkcie. W Euclid „s Elements , Proposition 4 księgi IV dowodzi, że ten punkt jest także środek okręgu wpisanego w trójkąt. Samo koło może być skonstruowane przez upuszczenie prostopadłej od środka do jednego z boków trójkąta i narysowanie okręgu z tym segmentem jako jego promieniem.

Środek leży w równych odległościach od trzech odcinków linii tworzących boki trójkąta, a także od trzech linii zawierających te odcinki. Jest to jedyny punkt jednakowo odległy od odcinków, ale są jeszcze trzy punkty jednakowo odległe od linii, z excenters, które tworzą ośrodki excircles danego trójkąta. Środek i mimośrody tworzą razem system ortocentryczny .

Przyśrodkowej oś wielokąta jest zbiór punktów, których najbliższy sąsiad na wielokąta nie jest unikalna: te punkty są w równej odległości od dwóch lub więcej boków wielokąta. Jedną z metod obliczania osi środkowych jest użycie transformacji typu grassfire , w której tworzy się ciągłą sekwencję krzywych przesunięcia , z których każda znajduje się w pewnej stałej odległości od wielokąta; oś środkowa jest śledzona przez wierzchołki tych krzywych. W przypadku trójkąta oś środkowa składa się z trzech segmentów dwusiecznych kąta, łączących wierzchołki trójkąta ze środkiem, który jest unikalnym punktem na najbardziej wewnętrznej krzywej przesunięcia. Prosty szkielet , określone w podobny sposób, z innego rodzaju przesunięcie krzywej pokrywa się ze środkowej osi do wypukłych wielokątów itd także posiada złącze na incenter.

Dowody

Dowód proporcji

Niech przecięcie i spotkanie w , i przecięcie i spotkanie w , i spotkanie w . ${\ Displaystyle \ kąt {BAC}}$${\displaystyle {\overline {BC}}}$${\ Displaystyle D}$${\ Displaystyle \ kąt {ABC}}$${\displaystyle {\overline {AC}}}$${\ Displaystyle E}$${\displaystyle {\overline {AD}}}$${\displaystyle {\overline {BE}}}$${\ Displaystyle {I}}$

I niech i spotka się o . ${\displaystyle {\overline {CI}}}$${\displaystyle {\overline {AB}}}$${\ Displaystyle {F}}$

Następnie musimy udowodnić, że jest to przecięcie . ${\displaystyle {\overline {CI}}}$${\ Displaystyle \ kąt {ACB}}$

W , . ${\ Displaystyle \ trójkąt {ACF}}$${\ Displaystyle {\ overline {AC}}: {\ overline {AF}} = {\ overline {CI}}: {\ overline {IF}}}$

W , . ${\ Displaystyle \ trójkąt {BCF}}$${\ Displaystyle {\ overline {BC}}: {\ overline {BF}} = {\ overline {CI}}: {\ overline {IF}}}$

Dlatego , tak , że . ${\ Displaystyle {\ overline {AC}}: {\ overline {AF}} = {\ overline {BC}}: {\ overline {BF}}}$${\ Displaystyle {\ overline {AC}}: {\ overline {BC}} = {\ overline {AF}}: {\ overline {BF}}}$

Więc jest to przecięcie${\displaystyle {\overline {CF}}}$${\ Displaystyle \ kąt {ACB}}$

Dowód prostopadły

Linia będąca dwusieczną kąta jest równoodległa od obu jej linii przy pomiarze prostopadłym. W miejscu, gdzie przecinają się dwie dwusieczne, punkt ten jest prostopadle równoodległy od linii tworzących kąt końcowy (ponieważ są one w tej samej odległości od przeciwległej krawędzi tego kąta), a zatem leży na jego dwusiecznej kąta.

Związek z bokami i wierzchołkami trójkąta

Współrzędne trójliniowe

Te współrzędne trójliniowego dla punktu w trójkącie uzyskując stosunek odległości do boków trójkąta. Współrzędne trójliniowe dla środka są podane przez

${\ Displaystyle \ 1:1:1.}$

Zbiorowi środków trójkątów można nadać strukturę grupy przy współrzędnym pomnożeniu współrzędnych trójliniowych; w tej grupie środek stanowi element tożsamości .

Współrzędne barycentryczne

W barycentryczne współrzędnych dla punktu w wag trójkąt dać takie, że punkt jest średnią ważoną położeń wierzchołków trójkąta. Współrzędne barycentryczne dla centrum są podane przez

${\ Displaystyle \ a:b:c}$

gdzie , , i są długościami boków trójkąta, lub równoważnie (używając prawa sinusów ) przez ${\displaystyle a}$${\displaystyle b}$${\displaystyle c}$

${\ Displaystyle \ grzech (A): \ grzech (B): \ grzech (C)}$

gdzie , i są kątami na trzech wierzchołkach. ${\ Displaystyle A}$${\ Displaystyle B}$${\displaystyle C}$

współrzędne kartezjańskie

Te współrzędne kartezjańskie z incenter są średnią ważoną współrzędnych trzech wierzchołków za pomocą długości boków trójkąta w stosunku do obwodu-IE, przy użyciu współrzędnych barycentryczną podane powyżej, znormalizowana do jedności do sumy jako ciężarki. (Wagi są pozytywne, to w incenter leży wewnątrz trójkąta, jak podano powyżej). Jeśli trzy wierzchołki są umieszczone w , i , a boki przeciwległych Wierzchołki te mają odpowiednie odcinki , i , następnie incenter jest ${\ Displaystyle (x_ {A}, Y_ {A})}$${\ Displaystyle (x_ {B}, Y_ {B})}$${\ Displaystyle (x_ {C}, Y_ {C})}$${\displaystyle a}$${\displaystyle b}$${\displaystyle c}$

${\ Displaystyle {\ Bigg (}{\ Frac {ax_ {A} + bx_ {B} + cx_ {C}} {a + b + c}}, {\ Frac {ay_ {A} + przez_ {B} + cy_{C}}{a+b+c}}{\bigg )}={\frac {a(x_{A},y_{A})+b(x_{B},y_{B})+c (x_{C},y_{C})}{a+b+c}}.}$

Odległości do wierzchołków

Oznaczając środek trójkąta ABC jako I , odległości od środka do wierzchołków połączone z długościami boków trójkąta są zgodne z równaniem

${\ Displaystyle {\ Frac {IA \ cdot IA} {CA \ cdot AB}} + {\ Frac {IB \ cdot IB} {AB \ cdot BC}} + {\ Frac {IC \ cdot IC} {BC \ cdot CA}}=1.}$

Dodatkowo,

${\ Displaystyle IA \ cdot IB \ cdot IC = 4 Rr ^ {2},}$

gdzie R i r są odpowiednio promieniem okręgu i promieniem trójkąta .

Powiązane konstrukcje

Inne ośrodki

Odległość od środka do środka ciężkości jest mniejsza niż jedna trzecia długości najdłuższej mediany trójkąta.

Z twierdzenia Eulera w geometrii , kwadrat odległości od środka I do środka opisanego O jest dana przez

${\ Displaystyle OI ^ {2} = R (R-2r)}$

gdzie R i r oznaczają odpowiednio promień i promień; w ten sposób obwód promienia jest co najmniej dwukrotnie większy od promienia, z równością tylko w przypadku równobocznym .

Odległość od centrum incenter do N w okrąg dziewięciu punktów jest

${\ Displaystyle IN = {\ Frac {1} {2}} (R-2r) < {\ Frac {1} {2}} R.}$

Odległość do kwadratu od środka do ortocentrum H wynosi

${\ Displaystyle IH ^ {2} = 2r ^ {2} -4 R ^ {2} \ cos A \ cos B \ cos C.}$

Nierówności obejmują:

${\ Displaystyle IG<HG,\quad IH<HG,\quad IG<IO,\quad 2IN<IO.}$

Incenter jest punkt Nagel z trójkąta środkowej (trójkąta, którego wierzchołki są punkty środkowe boków) i dlatego leży wewnątrz tego trójkąta. Odwrotnie, punkt Nagla dowolnego trójkąta jest środkiem jego trójkąta antykomplementarnego .

Środek musi leżeć we wnętrzu dysku, którego średnica łączy środek ciężkości G i ortocentrum H ( krążek ortocentryczny ), ale nie może pokrywać się z dziewięciopunktowym środkiem , którego położenie jest ustalone na 1/4 długości średnicy (bliżej G ). Każdy inny punkt w obrębie dysku ortocentroidalnego jest środkiem unikalnego trójkąta.

Linia Eulera

Prosta Eulera trójkąta jest linia przechodząca przez jego circumcenter , ciężkości i orthocenter między innymi punktami. Incenter na ogół nie leży na linii Eulera; znajduje się na linii Eulera tylko dla trójkątów równoramiennych , dla których linia Eulera pokrywa się z osią symetrii trójkąta i zawiera wszystkie środki trójkąta.

Oznaczając odległość od środka do linii Eulera jako d , długość najdłuższej mediany jako v , długość najdłuższego boku jako u , promień okręgu jako R , długość odcinka linii Eulera od ortocentrum do środka jako e , a półobwód jako s , zachodzą następujące nierówności:

${\displaystyle {\frac {d}{s}}<{\frac {d}{u}}<{\frac {d}{v}}<{\frac {1}{3}};}$

${\displaystyle d<{\frac {1}{3}}e;}$

${\displaystyle d<{\frac {1}{2}}R.}$

Rozdzielacze powierzchniowe i obwodowe

Każda linia przechodząca przez trójkąt, która dzieli zarówno obszar trójkąta, jak i jego obwód na pół, przechodzi przez środek trójkąta; każda linia przechodząca przez środek, która dzieli obszar na pół, dzieli również obwód na pół. W każdym trójkącie istnieje jedna, dwie lub trzy takie linie.

Odległości względne od dwusiecznej kąta

Niech X będzie zmiennym punktem na wewnętrznej dwusiecznej kąta A . Wtedy X = I (środek) maksymalizuje lub minimalizuje stosunek wzdłuż tej dwusiecznej kąta. ${\ Displaystyle {\ tfrac {BX} {CX}}}$

Bibliografia

Zewnętrzne linki

• Weisstein, Eric W. „Incenter” . MatematykaŚwiat .