Twierdzenie Nielsena-Schreiera - Nielsen–Schreier theorem

W teorii grup , gałąź matematyki The Nielsen-Schreier twierdzenie mówi, że każda podgrupa z wolną grupą jest się za darmo. Jego nazwa pochodzi od Jakoba Nielsena i Otto Schreiera .

Stwierdzenie twierdzenia

Wolną grupę można zdefiniować z prezentacji grupowej składającej się ze zbioru generatorów bez relacji. Oznacza to, że każdy element jest iloczynem jakiegoś ciągu generatorów i ich odwrotności, ale elementy te nie podlegają żadnym równaniom poza tymi, które wynikają trywialnie z gg ^-1 = 1. Elementy wolnej grupy można opisać jako wszystkie możliwe słowa zredukowane , te ciągi generatorów i ich odwrotności, w których żaden generator nie sąsiaduje z własną odwrotnością. Dwa zredukowane słowa można pomnożyć, łącząc je, a następnie usuwając wszelkie pary generator-odwrotność, które wynikają z połączenia.

Twierdzenie Nielsena-Schreiera stwierdza, że ​​jeśli H jest podgrupą wolnej grupy G , to sam H jest izomorficzny z wolną grupą. Oznacza to, że istnieje zbiór S elementów, które generują H , bez nietrywialnych relacji między elementami S .

Wzór Nielsena Schreier lub wzór wskaźnik Schreier , ilościowo rezultat w przypadku, gdy podgrupa ma wskaźnik skończoną: jeśli G jest wolna grupa rangi n (wolny od n generatorów), a H jest podgrupa skończonego indeksu [ G  : H ] = e , to H jest wolne od rangi . ${\ Displaystyle 1 + e (n {-} 1)}$

Przykład

Niech G będzie wolną grupą z dwoma generatorami , a H będzie podgrupą wszystkich zredukowanych słów o parzystej długości (iloczyny parzystej liczby liter ). Wtedy H jest generowane przez jego sześć elementów . Faktoryzacja dowolnego zredukowanego słowa w H do tych generatorów i ich odwrotności mogą być skonstruowane po prostu przez wzięcie kolejnych par liter w zredukowanym słowie. Nie jest to jednak swobodna prezentacja H, ponieważ ostatnie trzy generatory można zapisać w kategoriach pierwszych trzech jako . Raczej H jest generowane jako wolna grupa przez trzy elementy, które nie mają między sobą relacji; lub zamiast tego przez kilka innych trójek z sześciu generatorów. Dalej, G jest wolny na n = 2 generatorach, H ma indeks e = [ G  : H ] = 2 w G , a H jest wolny na 1 + e ( n –1) = 3 generatory. Twierdzenie Nielsena-Schreiera stwierdza, że ​​podobnie jak H , każda podgrupa wolnej grupy może być generowana jako wolna grupa, a jeśli indeks H jest skończony, jego rangę określa wzór na indeks. ${\displaystyle a,b}$${\ Displaystyle a, b, a ^ {-1}, b ^ {-1}}$${\ Displaystyle p = aa \ q = ab \ r = ba \ s = bb \ t = ab ^ {-1} \ u = a ^ {-1} b}$${\ Displaystyle s = rp ^ {-1} q \ t = pr ^ {-1} \ u = p ^ {-1} q}$${\ Displaystyle p=aa,\ q=ab,\ r=ba,}$

Dowód

Wolna grupa G = π ₁ ( X ) ma n = 2 generatory odpowiadające pętlom a , b od punktu bazowego P w X . Podgrupa H słów o parzystej długości, o indeksie e = [ G  : H ] = 2, odpowiada grafowi pokrywającemu Y z dwoma wierzchołkami odpowiadającymi cosetom H i H' = aH = bH = a- ¹ H = b ^{- 1} H i dwie uniesione krawędzie dla każdej z oryginalnych krawędzi pętli a , b . Skrócenie jednej z krawędzi Y daje homotopijną równoważność bukietowi trzech okręgów, tak że H = π ₁ ( Y ) jest wolną grupą na trzech generatorach, na przykład aa , ab , ba .

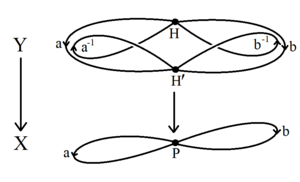
Krótki dowód twierdzenia Nielsena Schreier wykorzystuje algebraiczną topologii z podstawowych grup i przestrzeni obejmujących . Wolna grupa G na zbiorze generatorów jest podstawową grupą bukietu okręgów , grafu topologicznego X z pojedynczym wierzchołkiem i krawędzią pętli dla każdego generatora. Każda podgrupa H grupy podstawowej sama jest podstawową grupą połączonej przestrzeni pokrywającej Y → X. Przestrzeń Y jest (prawdopodobnie nieskończonym) grafem topologicznym, graf Schreiera coset ma jeden wierzchołek na każdy coset w G/H . W każdym połączonym grafie topologicznym możliwe jest zmniejszenie krawędzi drzewa opinającego grafu, tworząc bukiet okręgów, które mają tę samą grupę podstawową H . Ponieważ H jest podstawową grupą bukietu kół, samo w sobie jest bezpłatne.

Homologia uproszczona pozwala na obliczenie rangi H , która jest równa h ₁ ( Y ), pierwszej liczby Bettiego przestrzeni pokrywającej, liczby niezależnych cykli. Dla G bez rangi n graf X ma n krawędzi i 1 wierzchołek; zakładając, że H ma skończony indeks [ G  : H ] = e , graf pokrywający Y ma en krawędzi i e vertices. Pierwsza liczba Bettiego grafu jest równa liczbie krawędzi minus liczba wierzchołków plus liczba połączonych składowych; stąd ranga H to:

${\ Displaystyle h_ {1}(Y) \ = \ en-e + 1 \ = \ 1 + e (n {-} 1).}$

Dowód ten zawdzięczamy Reinholdowi Baerowi i Friedrichowi Levi  ( 1936 ); oryginalny dowód przez Schreier stanowi wykres Schreier w inny sposób, iloraz wykresie Cayley z G modulo działaniem H .

Zgodnie z lematem podgrupy Schreiera zbiór generatorów dla swobodnej prezentacji H może być skonstruowany z cykli w grafie pokrywającym utworzonym przez połączenie ścieżki drzewa opinającego od punktu bazowego (coset tożsamości) do jednego z kosetów, a pojedyncza krawędź niebędąca drzewem i odwrócona ścieżka drzewa opinającego od drugiego punktu końcowego krawędzi z powrotem do punktu bazowego.

Podstawy aksjomatyczne

Chociaż znanych jest kilka różnych dowodów twierdzenia Nielsena-Schreiera, wszystkie one zależą od aksjomatu wyboru . Na przykład w dowodzie opartym na fundamentalnych grupach bukietów aksjomat wyboru pojawia się pod postacią stwierdzenia, że ​​każdy graf połączony ma drzewo opinające. Użycie tego aksjomatu jest konieczne, ponieważ istnieją modele teorii mnogości Zermelo-Fraenkla, w których zarówno aksjomat wyboru, jak i twierdzenie Nielsena-Schreiera są fałszywe. Twierdzenie Nielsena-Schreiera z kolei implikuje słabszą wersję aksjomatu wyboru dla zbiorów skończonych.

Historia

Twierdzenie Nielsena-Schreiera jest nieabelowym odpowiednikiem starszego wyniku Richarda Dedekinda , że każda podgrupa wolnej grupy abelowej jest abelowa wolna .

Jakob Nielsen ( 1921 ) pierwotnie udowodnił ograniczoną formę twierdzenia, stwierdzając, że każda skończenie generowana podgrupa wolnej grupy jest wolna. Jego dowód polega na wykonaniu sekwencji przekształceń Nielsena na zbiorze generującym podgrupy, które zmniejszają ich długość (jako zredukowane słowa w wolnej grupie, z której zostały narysowane). Otto Schreier udowodnił twierdzenie Nielsena–Schreiera w całej jego ogólności w swojej pracy habilitacyjnej z 1926 r. Die Untergruppen der freien Gruppe , również opublikowanej w 1927 r. w Abh. matematyka. Sem. Hamburg. Uniw.

Dowód topologiczny oparty na podstawowych grupach wiązek okręgów jest dziełem Reinholda Baera i Friedricha Levi  ( 1936 ). Kolejny dowód topologicznej, na podstawie Bass-Serre teorii o działaniach grupowych na drzewach , została opublikowana przez Jean-Pierre Serre  ( 1970 ).

Zobacz też

• Podstawowe twierdzenie o grupach cyklicznych , podobny wynik dla grup cyklicznych, które w przypadku nieskończonym mogą być postrzegane jako szczególny przypadek twierdzenia Nielsena-Schreiera

Uwagi

Bibliografia

• Baer, ​​Reinhold ; Levi, Friedrich (1936), „Freie Produkte und ihre Untergruppen”, Compositio Mathematica , 3 : 391-398.
• Smażony, Michael D .; Jarden, Moshe (2008), Arytmetyka pola , Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, 11 (wyd. 3), Springer-Verlag , s. 70, numer ISBN 978-3-540-77269-9, Zbl  1145.12001.
• Howard, Paul E. (1985), „Podgrupy wolnej grupy i aksjomat wyboru”, The Journal of Symbolic Logic , 50 (2): 458-467, doi : 10.2307/2274234 , JSTOR  2274234 , MR  0793126.
• Johnson, DL (1980), Topics in the Theory of Group Presentations , seria wykładów London Mathematical Society, 42 , Cambridge University Press, ISBN 978-0-521-23108-4.
• Johnson, DL (1997), Prezentacje grup , teksty studenckie London Mathematical Society, 15 (wyd. 2), Cambridge University Press, ISBN 978-0-521-58542-2.
• Läuchli, Hans (1962), "Auswahlaxiom in der Algebra", Commentarii Mathematici Helvetici , 37 : 1-18, doi : 10.1007/bf02566957 , hdl : 20.500.11850/131689 , MR  0143705 , S2CID  186223589.
• Magnus, Wilhelm ; Karrass, Abraham; Solitar, Donald (1976), Teoria grup kombinatorycznych (wyd. 2 poprawione), Dover Publications.
• Nielsen, Jakob (1921), „Om regning med ikke-commutative faktorer og dens anvendelse i grouppeteorien”, Math. Tidsskrift B (w języku duńskim), 1921 : 78-94, JFM  48.0123.03.
• Rotman, Joseph J. (1995), Wprowadzenie do teorii grup , Graduate Texts in Mathematics, 148 (4th ed.), Springer-Verlag, ISBN 978-0-387-94285-8.
• Serre, J.-P. (1970), Groupes Discretes , Extrait de I'Annuaire du College de France, Paryż.
• Serre, J.-P. (1980), Drzewa , Springer-Verlag, ISBN 3-540-10103-9.
• Stillwell, John (1993), Topologia klasyczna i kombinatoryczna teoria grup , Teksty magisterskie z matematyki, 72 (2nd ed.), Springer-Verlag.