Termin (logika) - Term (logic)

W logice matematycznej , A termin oznacza obiektowi matematycznemu zaś formuła oznacza matematycznego fakt. W szczególności terminy pojawiają się jako składniki formuły. Jest to analogiczne do języka naturalnego, gdzie fraza rzeczownikowa odnosi się do przedmiotu, a całe zdanie odnosi się do faktu.

Pierwszego rzędu Termin rekurencyjnym konstruowane ze stałych symboli zmiennych i symboli funkcyjnych . Wyrażenie utworzona przez nakładanie źródłowe symbolu do odpowiedniej liczby terminów jest zwany wzór atomowej , które ma wartość prawdziwą lub FAŁSZ w dwuwartościowych logiki , podawany jest interpretacja . Na przykład jest terminem zbudowanym ze stałej 1, zmiennej x i symboli funkcji binarnych i ; jest to część wzoru atomowego, który oblicza się jako prawdziwy dla każdej wartości liczbowej x . ${\ Displaystyle (x+1)*(x+1)}$${\displaystyle +}$${\ Displaystyle *}$${\ Displaystyle (x + 1) * (x + 1) \ geq 0}$

Poza logiką terminy odgrywają ważną rolę w algebrze uniwersalnej i systemach przepisywania .

Formalna definicja

Struktura drzewiasta terminów ( n ⋅( n +1))/2 i n ⋅(( n +1)/2)

Biorąc pod uwagę zestaw V zmiennych symboli, zestaw C stałych symboli i zestawy F _n o n symboli funkcyjnych -ary, zwane symbolami operatora, dla każdej liczby naturalne n ≥ 1, przy czym zestaw (bez sortowania pierwszorzędowa) warunki T jest rekurencyjnie definiowany jako najmniejszy zestaw o następujących właściwościach:

• każdy symbol zmiennej jest wyrazem: V ⊆ T ,
• każdy symbol stały jest wyrazem: C ⊆ T ,
• z każdego n wyrazów t ₁ ,..., t _n , i każdego n- argumentowego symbolu funkcji f ∈ F _n , można zbudować większy wyraz f ( t ₁ , ..., t _n ).

Korzystanie intuicyjny, pseudo- gramatyczne zapis, to jest czasami pisany jako: t  :: = x | c | f ( t ₁ , ..., t _n ). Zazwyczaj tylko pierwsze kilka funkcji kodowe C _n zamieszkanych. Dobrze znanymi przykładami są symbole funkcji jednoargumentowych sin , cos ∈ F ₁ , oraz symbole funkcji binarnych +, −, ⋅, / ∈ F ₂ , podczas gdy operacje trójskładnikowe są mniej znane, nie mówiąc już o funkcjach o wyższej arności. Wielu autorów uważa symbole stałe za symbole funkcji 0-argumentowych F ₀ , a zatem nie potrzebują dla nich specjalnej klasy składniowej.

Termin oznacza przedmiot matematyczny z dziedziny dyskursu . Stała c oznacza nazwany obiekt z tej dziedziny, zmienna x obejmuje obiekty w tej dziedzinie, a funkcja n- argumentowa f odwzorowuje n - krotki obiektów na obiekty. Na przykład, jeśli n ∈ V jest symbolem zmiennym, 1 ∈ C jest symbolem stałym, a add ∈ F ₂ jest symbolem funkcji binarnej, to n ∈ T , 1 ∈ T i (stąd) add ( n , 1) ∈ T odpowiednio przez pierwszą, drugą i trzecią regułę budowania składu. Ten ostatni termin jest zwykle zapisywany jako n +1, przy użyciu notacji wrostkowej i bardziej popularnego symbolu operatora + dla wygody.

Struktura terminowa a reprezentacja

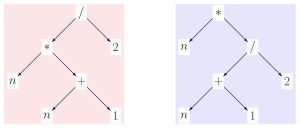
Pierwotnie logicy definiowali termin jako ciąg znaków przestrzegający pewnych zasad budowania. Jednak odkąd koncepcja drzewa stała się popularna w informatyce, wygodniej było myśleć o tym terminie jako o drzewie. Na przykład kilka odrębnych ciągów znaków, takich jak " ( n ⋅( n +1))/2 ", " (( n ⋅( n +1)))/2 " i " ", oznacza ten sam termin i odpowiada to samo drzewo, mianowicie. lewe drzewo na powyższym obrazku. Oddzielając strukturę drzewiastą termu od jego graficznej reprezentacji na papierze, łatwo jest również uwzględnić nawiasy (będące tylko reprezentacją, a nie strukturą) i niewidoczne operatory mnożenia (istniejące tylko w strukturze, a nie w reprezentacji). ${\displaystyle {\frac {n(n+1)}{2}}}$

Równość strukturalna

Mówi się, że dwa terminy są strukturalnie , dosłownie lub składniowo równe , jeśli odpowiadają temu samemu drzewu. Na przykład, w lewo i prawo drzewo na powyższym zdjęciu są strukturalnie un równych warunkach, chociaż mogą być one uznane za „ semantycznie równy ”, ponieważ zawsze oceniać na tę samą wartość w racjonalnym arytmetyki . Podczas gdy równość strukturalną można sprawdzić bez wiedzy o znaczeniu symboli, równość semantyczna nie. Jeśli funkcja / jest np. interpretowana nie jako wymierna, ale jako obcinanie dzielenia liczb całkowitych , to przy n =2 lewy i prawy wyraz dają odpowiednio 3 i 2. Strukturalne terminy równości muszą być zgodne w nazwach zmiennych.

W przeciwieństwie do tego, termin t nazywany jest zmianą nazwy lub wariantem terminu u, jeśli ten ostatni wynikał z konsekwentnej zmiany nazwy wszystkich zmiennych tego pierwszego, tj. jeśli u = tσ dla jakiegoś podstawienia zmiany nazwy σ. W takim przypadku u jest również zmianą nazwy t , ponieważ podstawienie zmiany nazwy σ ma odwrotność σ ⁻¹ , a t = uσ ⁻¹ . Oba terminy są wtedy również określane jako równe zmiany nazwy modulo . W wielu kontekstach poszczególne nazwy zmiennych w wyrażeniu nie mają znaczenia, np. aksjomat przemienności dla dodawania można określić jako x + y = y + x lub jako a + b = b + a ; w takich przypadkach można zmienić nazwę całego wzoru, podczas gdy dowolny podtermin zwykle nie może, np. x + y = b + a nie jest poprawną wersją aksjomatu przemienności.

Warunki gruntowe i liniowe

Zbiór zmiennych wyrazu t jest oznaczony przez vars ( t ). Termin, który nie zawiera żadnych zmiennych, nazywa się terminem podstawowym ; termin, który nie zawiera wielu wystąpień zmiennej, nazywany jest terminem liniowym . Na przykład 2+2 jest członem podstawowym, a zatem także członem liniowym, x ⋅( n +1) jest członem liniowym, n ⋅( n +1) jest członem nieliniowym. Te właściwości są ważne np . przy przepisaniu terminów .

Mając sygnaturę symboli funkcyjnych, zbiór wszystkich terminów tworzy algebrę wyrazu wolnego . Zbiór wszystkich termów podstawowych tworzy algebrę termu początkowego .

Skrótując liczbę stałych jako f ₀ , a liczbę symboli funkcji i- arnych jako f _i , liczbę θ _h różnych wyrazów podstawowych o wysokości do h można obliczyć za pomocą następującego wzoru rekurencji:

• θ ₀ = f ₀ , ponieważ człon podstawowy o wysokości 0 może być tylko stałą,
• ${\ Displaystyle \ theta _ {h + 1} = \ suma _ {i = 0} ^ {\ infty} f_ {i} \ cdot \ theta _ {h} ^ {i}}$, ponieważ warunek podstawowy o wysokości do h +1 można uzyskać przez złożenie dowolnych i termów podstawowych o wysokości do h , używając i- arnego symbolu funkcji pierwiastka. Suma ma skończoną wartość, jeśli istnieje tylko skończona liczba stałych i symboli funkcji, co zwykle ma miejsce.

Budowanie formuł z terminów

Biorąc pod uwagę zestaw R _n o n -ary symboli relacji dla każdej liczby naturalne n ≥ 1 przedstawiono (bez sortowania pierwszorzędowa) Wzór atomowy uzyskuje się poprzez przykładanie n -ary związku symbol n warunkach. Jeśli chodzi o symbole funkcyjne, zestaw symboli relacji R _n jest zwykle niepusty tylko dla małego n . W logice matematycznej bardziej złożone formuły są budowane z formuł atomowych przy użyciu spójników logicznych i kwantyfikatorów . Na przykład, pozwalając na oznaczenie zbioru liczb rzeczywistych , ∀ x : x ∈ ⇒ ( x +1)⋅( x +1) ≥ 0 jest formułą matematyczną, która w algebrze liczb zespolonych jest równa prawdziwości . Formuła atomowa nazywana jest ziemią, jeśli jest zbudowana całkowicie z pojęć podstawowych; wszystkie podstawowe formuły atomowe, które można skomponować z danego zestawu symboli funkcji i predykatów, tworzą bazę Herbranda dla tych zestawów symboli. ${\ Displaystyle \ mathbb {R}}$${\ Displaystyle \ mathbb {R}}$

Operacje z terminami

Struktura drzewiasta czarnego przykładowego terminu , z niebieskim redeksem${\ Displaystyle {\ Frac {a * ((a + 1) * (a + 2) {1 * (2 * 3)}}}$${\ Displaystyle x * (y * z)}$

• Ponieważ termin ma strukturę hierarchii drzewa, każdemu z jego węzłów można przypisać pozycję lub ścieżkę , czyli ciąg liczb naturalnych wskazujących miejsce węzła w hierarchii. Pusty ciąg, zwykle oznaczany przez ε, jest przypisywany do węzła głównego. Łańcuchy pozycyjne w obrębie czarnego terminu są zaznaczone na rysunku kolorem czerwonym.
• W każdej pozycji p wyrazu t rozpoczyna się unikalny podtermin , który jest powszechnie oznaczany przez t | _s . . Na przykład w pozycji 122 czarnego wyrazu na obrazku podczłon a +2 ma swój pierwiastek. Relacja „jest podterminem” jest częściowym porządkiem zbioru terminów; jest zwrotny, ponieważ każdy termin jest trywialnie podterminem samym w sobie.
• Wyraz otrzymany przez zastąpienie w wyrażeniu t podwyrazu w pozycji p nowym wyrazem u jest powszechnie oznaczany przez t [ u ] _p . Termin t [ u ] _p może być również postrzegany jako wynik uogólnionego połączenia terminu u z obiektem podobnym do terminu t [.] ; to ostatnie nazywa się kontekstem lub terminem z otworem (oznaczonym przez „.”; jego pozycja to p ), w którym mówi się, że osadzony jest u . Na przykład, jeśli t jest czarnym wyrazem na rysunku, to t [ b +1] ₁₂ daje wyraz . Ten ostatni termin wynika również z osadzenia terminu b +1 w kontekście . W sensie nieformalnym operacje tworzenia instancji i osadzania są odwrotne do siebie: podczas gdy pierwsza dodaje symbole funkcji na dole terminu, druga dodaje je na górze. Zamówienie obejmujące dotyczy terminu i dowolnego wyniku załączników po obu stronach.${\ Displaystyle {\ Frac {a * (b + 1) {1 * (2 * 3)}}}$${\displaystyle {\frac {a*(\;.\;)}{1*(2*3)}}}$
• Każdemu węzłowi terminu można przypisać jego głębokość (zwaną przez niektórych autorów wysokością ), czyli odległość (liczbę krawędzi) od korzenia. W tym ustawieniu głębokość węzła jest zawsze równa długości ciągu jego pozycji. Na rysunku poziomy głębokości w czarnym terminie są zaznaczone na zielono.
• Wielkość z terminem powszechnie odnosi się do liczby węzłami lub równoważnie długości pisemnej reprezentacji którego się odnosi, licząc symboli bez nawiasów. Czarny i niebieski termin na zdjęciu ma odpowiednio rozmiar 15 i 5.
• Termin u pasuje do terminu t , jeśli instancja podstawienia u strukturalnie równa się podterminowi t , lub formalnie, jeśli u σ = t | _p dla pewnej pozycji p w t i pewnego podstawienia σ. W tym przypadku, U , T , i σ nazywane są określenie wzorca , do określenia przedmiotu , a podstawienie dopasowanie , odpowiednio. Na rysunku niebieski wzorzec termin odpowiada czerni termin przedmiot w pozycji 1, z dopasowanym podstawienia { x ↦ a , y ↦ a +1, Z ↦ +2} wskazanym przez zmienne niebieskie natychmiast pozostawione czarnych zastępczych. Intuicyjnie, wzór, z wyjątkiem jego zmiennych, musi być zawarty w podmiocie; jeśli zmienna występuje we wzorcu wielokrotnie, w odpowiednich pozycjach podmiotu wymagane są równe podwarunki.${\ Displaystyle x * (y * z)}$
• ujednolicenie warunków
• przepisywanie terminów

Pojęcia pokrewne

Posortowane terminy

Gdy dziedzina dyskursu zawiera elementy zasadniczo różnego rodzaju, warto odpowiednio podzielić zbiór wszystkich terminów. W tym celu do każdej zmiennej i każdego symbolu stałej przypisywany jest sort (czasami nazywany typem ), a do każdego symbolu funkcji deklaracja sortowania dziedzinowego i sortowania zakresowego. Sortowane termin f ( T ₁ , ..., T _n ) może być złożony z sortowanych subterms t ₁ , ..., T _n tylko wtedy, jeżeli ı sortowania TH subterm pasuje deklarowana I th domeny rodzaju f . Taki termin jest również nazywany dobrze posortowanym ; każdy inny termin (tj. przestrzeganie tylko reguł nieposortowanych ) jest nazywany źle posortowanym .

Na przykład, przestrzeń wektorowa ma skojarzone pole liczb skalarnych. Niech W i N oznaczają odpowiednio rodzaj wektorów i liczb, V _W i V _N będą odpowiednio zbiorem zmiennych wektorowych i liczbowych, a C _W i C _N odpowiednio zbiorem stałych wektorowych i liczbowych. Wtedy np. i 0 ∈ C _N , a dodawanie wektorów, mnożenie przez skalar i iloczyn skalarny są deklarowane odpowiednio jako , i . Zakładając zmienne symbole i a , b ∈ V _N , termin jest dobrze posortowany, podczas gdy nie jest (ponieważ + nie akceptuje terminu sortowania N jako drugiego argumentu). Aby uzyskać dobrze posortowany termin, wymagana jest dodatkowa deklaracja . Symbole funkcyjne posiadające kilka deklaracji są nazywane przeciążonymi . ${\ Displaystyle {\ vec {0}} \ w C_ {W}}$${\ Displaystyle +: W \ razy W \ do W,*: W \ razy N \ do W}$${\ Displaystyle \ langle.,. \ rangle: W \ razy W \ do N}$${\ Displaystyle {\ vec {v}}, {\ vec {w}} \ w V_ {W}}$${\ Displaystyle \ langle ({\ vec {v}} + {\ vec {0}}) * a {\ vec {w}} * b \ rangle}$${\displaystyle {\vec {v}}+a}$${\displaystyle a*{\vec {v}}}$${\ Displaystyle *: N \ razy W \ do W}$

Zobacz logika o wielu sortowaniu, aby uzyskać więcej informacji, w tym rozszerzenia opisanej tutaj struktury o wielu sortowaniach .

Terminy lambda

Terminy z powiązanymi zmiennymi

Przykład notacji	Zmienne powiązane	Darmowe zmienne	Zapisane jako lambda-term
Limn →∞ x / n	n	x	granica (λ n . div ( x , n ))
${\ Displaystyle \ suma _ {i = 1} ^ {n} i ^ {2}}$	i	n	suma (1, n ,λ i . moc ( i ,2))
${\ Displaystyle \ int _ {a} ^ {b} \ grzech (k \ cdot t) dt}$	T	a , b , k	całka ( a , b ,λ t . sin ( k ⋅ t ))

Motywacja

Notacje matematyczne pokazane w tabeli nie pasują do schematu terminu pierwszego rzędu zdefiniowanego powyżej , ponieważ wszystkie wprowadzają własną lokalną lub powiązaną zmienną, która może nie pojawiać się poza zakresem notacji, np. nie ma sensu . Natomiast inne zmienne, określane jako free , zachowują się jak zwykłe zmienne terminów pierwszego rzędu, np. ma sens. ${\ Displaystyle t \ cdot \ int _ {a} ^ {b} \ grzech (k \ cdot t) \; dt}$${\ Displaystyle k \ cdot \ int _ {a} ^ {b} \ grzech (k \ cdot t) \; dt}$

Wszystkie te operatory można postrzegać jako przyjmujące funkcję, a nie termin wartości jako jeden ze swoich argumentów. Na przykład operator lim jest stosowany do sekwencji, tj. do odwzorowania z dodatniej liczby całkowitej na np. liczby rzeczywiste. Jako inny przykład, funkcja C implementująca drugi przykład z tabeli, Σ, miałaby argument wskaźnika funkcji (patrz ramka poniżej).

Terminy lambda mogą być używane do oznaczenia funkcji anonimowych, które mają być dostarczone jako argumenty do lim , Σ, ∫ itp.

Na przykład kwadrat funkcyjny z poniższego programu w języku C można zapisać anonimowo jako wyrażenie lambda λ i . I ² . Ogólny operator sumy Σ może być wtedy uważany za symbol funkcji trójskładnikowej przyjmujący wartość dolnej granicy, wartość górnej granicy i funkcję do zsumowania. Ze względu na ten ostatni argument, operator Σ jest nazywany symbolem funkcji drugiego rzędu . Jako inny przykład, termin lambda λ n . x / n oznacza funkcję, która odwzorowuje odpowiednio 1, 2, 3, ... na x /1, x /2, x /3, ..., czyli oznacza sekwencję ( x /1, x / 2, x /3, ...). Lim operator wykonuje takiej sekwencji i zwraca wartość graniczną (jeżeli podane wyżej).

Kolumna z prawej strony tabeli wskazuje, w jaki sposób każdy przykład notacji matematycznej może być reprezentowany przez termin lambda, a także konwertuje wspólne operatory infiksowe na formę prefiksu .

int sum(int lwb, int upb, int fct(int)) {    // implements general sum operator
    int res = 0;
    for (int i=lwb; i<=upb; ++i)
        res += fct(i);
    return res;
}

int square(int i) { return i*i; }            // implements anonymous function (lambda i. i*i); however, C requires a name for it

#include <stdio.h>
int main(void) {
    int n;
    scanf(" %d",&n);
    printf("%d\n", sum(1, n, square));        // applies sum operator to sum up squares
    return 0;
}

Definicja

Zobacz też

• Równanie
• Wyrażenie (matematyka)

Uwagi

Bibliografia

• Franza Baadera ; Tobiasza Nipkowa (1999). Przepisywanie terminów i tak dalej . Wydawnictwo Uniwersytetu Cambridge. s. 1–2 i 34–35. Numer ISBN 978-0-521-77920-3.