Metoda twierdzeń mechanicznych -The Method of Mechanical Theorems

Metoda twierdzeń mechanicznych ( gr . Περὶ μηχανικῶν θεωρημάτων πρὸς Ἐρατοσθένη ἔφοδος ) , zwana także metodą , jest uważana za jedno z najważniejszych zachowanych dzieł starożytnego greckiego erudyta Archimedesa . Metoda przyjmuje formę listu Archimedesa do Eratostenesa , głównego bibliotekarza w Bibliotece Aleksandryjskiej i zawiera pierwsze potwierdzone wyraźne użycie niepodzielności (czasami błędnie określane jako nieskończenie małe ). Dzieło pierwotnie uważano za zaginione, ale w 1906 r. zostało ponownie odkryte w słynnym Archimedes Palimpsest . Palimpsest zawiera opis Archimedesa o „metodzie mechanicznej”, tak zwanej, ponieważ opiera się na środku ciężaru figur ( centroid ) i prawie dźwigni , które po raz pierwszy zostały zademonstrowane przez Archimedesa w O równowadze płaszczyzn .

Archimedes nie dopuszczał metody niepodzielności jako części ścisłej matematyki i dlatego nie publikował swojej metody w formalnych traktatach zawierających wyniki. W tych traktatach udowadnia te same twierdzenia przez wyczerpanie , znajdując rygorystyczne górne i dolne granice, które zbiegają się do wymaganej odpowiedzi. Niemniej jednak metoda mechaniczna była tym, co wykorzystywał do odkrywania relacji, na które później dał rygorystyczne dowody.

Obszar paraboli

Aby wyjaśnić dzisiejszą metodę Archimedesa, wygodnie jest wykorzystać trochę geometrii kartezjańskiej, choć ta oczywiście była wówczas niedostępna. Jego pomysł polega na wykorzystaniu prawa dźwigni do wyznaczenia obszarów figur od znanego środka masy innych figur. Najprostszym przykładem we współczesnym języku jest obszar paraboli. Archimedes używa bardziej eleganckiej metody, ale w języku kartezjańskim jego metoda polega na obliczaniu całki

{\ Displaystyle \ int _ {0} ^ {1} x ^ {2} \ dx = {\ Frac {1} {3}}}

które w dzisiejszych czasach można łatwo sprawdzić za pomocą elementarnego rachunku całkowego .

Chodzi o to, aby mechanicznie zrównoważyć parabolę (zakrzywiony obszar zintegrowany powyżej) z pewnym trójkątem wykonanym z tego samego materiału. Paraboli jest regionem w płaszczyźnie między -osiowy a krzywa a wynosi od 0 do 1. Trójkąt jest regionem w tej samej płaszczyźnie pomiędzy -osiowy i linii , jak również zmienia się od 0 do 1. $(x,y)$ $x$ ${\ Displaystyle y = x ^ {2}}$ $x$ $x$ $y=x$ $x$

Pokrój parabolę i trójkąt na pionowe plasterki, po jednym dla każdej wartości . Wyobraź sobie, że oś - to dźwignia z punktem podparcia w . Prawo dźwigni stwierdza, że dwa obiekty po przeciwnych stronach punktu podparcia zrównoważy jeśli każdy ma ten sam moment , w którym moment obrotowy obiekt jest równa jego masie razy dystans do punktu podparcia. Dla każdej wartości , wycinek trójkąta na pozycji ma masę równą jego wysokości i znajduje się w pewnej odległości od punktu podparcia; więc zrównoważyłby odpowiedni kawałek paraboli o wysokości , gdyby ten ostatni został przesunięty do , w odległości 1 po drugiej stronie punktu podparcia. $x$ $x$ $x=0$ $x$ $x$ $x$ $x$ $x^{2}$ $x=-1$

Zrównoważony trójkąt i spandrel paraboliczny metodą

Ponieważ każda para plasterków równoważy się, przesunięcie całej paraboli do zrównoważy cały trójkąt. Oznacza to, że jeśli oryginalna nieprzecięta parabola zostanie zawieszona na haku z punktu (tak, aby cała masa paraboli była przymocowana do tego punktu), zrównoważy trójkąt znajdujący się między i . $x=-1$ $x=-1$ $x=0$ $x=1$

Środek masy trójkąta można łatwo znaleźć następującą metodą, również dzięki Archimedesowi. Jeśli linia środkowa zostanie narysowana od dowolnego wierzchołka trójkąta do przeciwległej krawędzi , trójkąt zrównoważy się na środku, uważanym za punkt podparcia. Powodem jest to, że jeśli trójkąt jest podzielony na nieskończenie małe odcinki równoległe do , każdy odcinek ma jednakową długość po przeciwnych stronach mediany, więc równowaga wynika z symetrii. Ten argument można łatwo uściślić przez wyczerpanie , używając małych prostokątów zamiast nieskończenie małych linii, i to właśnie robi Archimedes w O równowadze płaszczyzn . ${\ Displaystyle E}$ ${\ Displaystyle E}$

Zatem środek masy trójkąta musi znajdować się w punkcie przecięcia median. W przypadku omawianego trójkąta jedna mediana to linia , a druga mediana to linia . Rozwiązując te równania, widzimy, że przecięcie tych dwóch środkowych znajduje się powyżej punktu , więc całkowity wpływ trójkąta na dźwignię jest taki, jakby całkowita masa trójkąta napierała na ten punkt (lub zwisała z niego). Całkowity moment wywierany przez trójkąt to jego powierzchnia, 1/2 razy odległość 2/3 jego środka masy od punktu podparcia w . Ten moment obrotowy 1/3 równoważy parabolę, która znajduje się w odległości 1 od punktu podparcia. Stąd powierzchnia paraboli musi wynosić 1/3, aby nadać jej przeciwny moment obrotowy. $y=x/2$ $y=1-x$ ${\ Displaystyle x = 2/3}$ $x=0$

Ten typ metody może być użyty do znalezienia pola dowolnego odcinka paraboli, a podobne argumenty mogą być użyte do znalezienia całki dowolnej potęgi z , chociaż wyższe potęgi komplikują się bez algebry. Archimedes posunął się tylko do całki z , której używał do znajdowania środka masy półkuli, aw innych pracach środka masy paraboli. $x$ ${\ Displaystyle x ^ {3}}$

Pierwsza propozycja w palimpseście

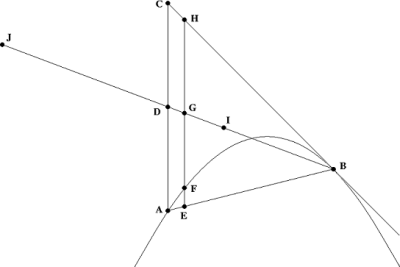
Rozważ parabolę na rysunku po prawej. Wybierz dwa punkty na paraboli i nazwij je A i B .

Załóżmy, że odcinek AC jest równoległy do osi symetrii paraboli. Załóżmy dalej, że odcinek linii BC leży na linii stycznej do paraboli w punkcie B . Pierwsza propozycja mówi:

Pole trójkąta ABC jest dokładnie trzykrotnością pola ograniczonego przez parabolę i sieczną AB .

Dowód :

Niech D będzie środkiem AC . Skonstruuj odcinek linii od JB do D , gdzie odległość od J do D jest równa odległości od B do D . Pomyślmy o segmencie JB jako o „dźwigni” z D jako punktem podparcia. Jak wcześniej wykazał Archimedes, środek masy trójkąta znajduje się w punkcie I na „dźwigni”, gdzie DI : DB = 1:3. Dlatego wystarczy wykazać, że jeśli cały ciężar wnętrza trójkąta spoczywa w I , a cały ciężar przekroju paraboli w J , to dźwignia jest w równowadze.

Rozważmy nieskończenie mały przekrój trójkąta określonego przez odcinek HE , gdzie punkt H leży na BC , punkt E leży na AB , a HE jest równoległy do osi symetrii paraboli. Nazwijmy przecięcie HE i paraboli F oraz przecięcie HE i dźwigni G . Jeżeli cały ciężar trójkąta spoczywa na I , wywiera on taki sam moment obrotowy na dźwignię JB jak na HE . Zatem chcemy pokazać, że jeżeli ciężar przekroju HE spoczywa na G, a ciężar przekroju EF przekroju paraboli na J , to dźwignia jest w równowadze. Innymi słowy, wystarczy pokazać, że EF : GD = EH : JD . Ale to rutynowa konsekwencja równania paraboli. CO BYŁO DO OKAZANIA

Objętość kuli

Ponownie, aby oświetlić metodę mechaniczną, wygodnie jest użyć trochę geometrii współrzędnych. Jeśli kula o promieniu 1 zostanie umieszczona ze środkiem w x = 1, pionowy promień przekroju poprzecznego w dowolnym x pomiędzy 0 a 2 jest określony następującym wzorem: ${\ Displaystyle \ rho _ {S}}$

{\ Displaystyle \ rho _ {S} (x) = {\ sqrt {x (2-x)}}.}

Masa tego przekroju do wyważenia na dźwigni jest proporcjonalna do powierzchni:

{\ Displaystyle \ pi \ rho _ {S} (x) ^ {2} = 2 \ pi x- \ pi x ^ {2}.}

Archimedes rozważał następnie obrócenie trójkątnego obszaru między y = 0 i y = x i x = 2 na płaszczyźnie x - y wokół osi x , aby utworzyć stożek. Przekrój tego stożka to okrąg o promieniu ${\ Displaystyle \ rho _ {C}}$

{\ Displaystyle \ rho _ {C} (x) = x}

a powierzchnia tego przekroju wynosi

{\ Displaystyle \ pi \ rho _ {C} ^ {2} = \ pi x ^ {2}.}

Tak więc, jeżeli plasterki stożka i kuli zarówno mają być ważone razem połączone powierzchnia przekroju poprzecznego jest:

{\ Displaystyle M (x) = 2 \ pi x.}

Jeśli dwie plastry zostaną umieszczone razem w odległości 1 od punktu podparcia, ich całkowita waga będzie dokładnie zrównoważona przez okrąg o powierzchni w odległości x od punktu po drugiej stronie. Oznacza to, że stożek i kula razem, gdyby cały ich materiał został przesunięty do x = 1 , zrównoważyłyby walec o promieniu podstawy 1 i długości 2 po drugiej stronie. $2\pi$

Ponieważ x waha się od 0 do 2, środek ciężkości cylindra będzie znajdował się w odległości 1 od punktu podparcia, więc cały ciężar cylindra można uznać za znajdujący się w pozycji 1. Stan równowagi zapewnia, że objętość stożka plus objętość kuli jest równa objętości cylindra.

Objętość cylindra to pole przekroju poprzecznego pomnożone przez wysokość, która wynosi 2, lub . Archimedes mógł również obliczyć objętość stożka za pomocą metody mechanicznej, ponieważ we współczesnych terminach całka, której dotyczy, jest dokładnie taka sama jak dla pola paraboli. Objętość stożka wynosi 1/3 jego podstawy razy wysokość. Podstawą stożka jest okrąg o promieniu 2, z polem , a wysokość to 2, więc pole to . Odjęcie objętości stożka od objętości cylindra daje objętość kuli: $2\pi$ $4\pi$ $4\pi$ $8\pi/3$

{\ Displaystyle V_ {S} = 4 \ pi - {8 \ ponad 3} \ pi = {4 \ ponad 3} \ pi.}

Zależność objętości kuli od promienia jest oczywista ze skalowania, choć wtedy też nie było to trywialne, aby było to rygorystyczne. Metoda daje następnie znany wzór na objętość kuli . Dzięki liniowemu skalowaniu wymiarów Archimedes z łatwością rozszerzył wynik objętości na sferoidy .

Argument Archimedesa jest prawie identyczny z argumentem powyżej, ale jego cylinder miał większy promień, tak że stożek i cylinder zwisały w większej odległości od punktu podparcia. Uważał ten argument za swoje największe osiągnięcie, prosząc, aby towarzysząca mu figura zrównoważonej kuli, stożka i cylindra została wygrawerowana na jego nagrobku.

Powierzchnia kuli

Aby znaleźć pole powierzchni kuli, Archimedes argumentował, że tak samo, jak pole powierzchni koła można traktować jako nieskończenie wiele nieskończenie małych trójkątów prostokątnych okrążających obwód (patrz Pomiar koła ), można pomyśleć o objętości kuli podzielony na wiele stożków o wysokości równej promieniowi i podstawie na powierzchni. Wszystkie stożki mają tę samą wysokość, więc ich objętość wynosi 1/3 powierzchni podstawy razy wysokość.

Archimedes stwierdza, że całkowita objętość kuli jest równa objętości stożka, którego podstawa ma taką samą powierzchnię jak kula i którego wysokość jest promieniem. Nie ma żadnych szczegółów dotyczących tej argumentacji, ale oczywistym powodem jest to, że stożek można podzielić na nieskończenie małe stożki, dzieląc obszar podstawy w górę, a każdy stożek wnosi wkład zgodnie ze swoim obszarem podstawy, tak samo jak w sferze .

Niech powierzchnia kuli to S . Objętość stożka o podstawie S i wysokości r wynosi , co musi być równe objętości kuli: . Dlatego pole powierzchni kuli musi wynosić , czyli "czterokrotność jej największego okręgu". Archimedes udowadnia to rygorystycznie w Na sferze i cylindrze . ${\ Displaystyle Sr/3}$ ${\ Displaystyle 4 \ pi r ^ {3}/3}$ ${\ Displaystyle 4 \ pi r ^ {2}}$

Kształty krzywoliniowe o objętościach wymiernych

Jedną z niezwykłych rzeczy w Metodzie jest to, że Archimedes znajduje dwa kształty określone przez sekcje walców, których objętość nie obejmuje , pomimo kształtów mających krzywoliniowe granice. Jest to centralny punkt badań — niektóre kształty krzywoliniowe można korygować za pomocą linijki i cyrkla, dzięki czemu istnieją nietrywialne, racjonalne relacje między objętościami wyznaczonymi przez przecięcia brył geometrycznych. $\pi$

Archimedes podkreśla to na początku traktatu i zachęca czytelnika, aby spróbował odtworzyć wyniki inną metodą. W przeciwieństwie do innych przykładów, objętość tych kształtów nie jest rygorystycznie obliczona w żadnej z jego innych prac. Z fragmentów palimpsestu wynika, że Archimedes zapisał i opisał kształty, aby udowodnić rygorystyczne ograniczenia objętości, chociaż szczegóły nie zostały zachowane.

Dwa kształty, które rozważa, to przecięcie dwóch prostopadłych walców ( bicylinder ), czyli obszar ( x , y , z ) przestrzegający:

{\ Displaystyle x ^ {2} + r ^ {2} < 1, \ quad y ^ {2} + z ^ {2} < 1,}

oraz graniastosłup kołowy, czyli region podległy:

x^{2}+y^{2}<1,\quad 0<z<y

Oba problemy mają cięcie, które daje łatwą całkę dla metody mechanicznej. W przypadku okrągłego pryzmatu pokrój oś x na plasterki. Obszar w płaszczyźnie y - z w dowolnym x jest wnętrzem trójkąta prostokątnego o długości boku, którego pole wynosi , tak że całkowita objętość wynosi:

{\ Displaystyle {\ sqrt {1-x ^ {2}}}}

{\ Displaystyle {1 \ ponad 2} (1-x ^ {2})}

{\ Displaystyle \ Displaystyle \ int _ {-1} ^ {1} {1 \ ponad 2} (1-x ^ {2}) \ dx}

które można łatwo naprawić metodą mechaniczną. Dodanie do każdego trójkątnego przekroju części trójkątnej piramidy o powierzchni równoważy pryzmat, którego przekrój jest stały.

{\ Displaystyle x ^ {2}/2}

W przypadku przecięcia dwóch cylindrów cięcie jest tracone w rękopisie, ale można je zrekonstruować w oczywisty sposób równolegle do reszty dokumentu: jeśli płaszczyzna xz jest kierunkiem cięcia, równania dla cylindra dają to, podczas gdy , który definiuje obszar będący kwadratem w płaszczyźnie x - z o długości boku , tak aby całkowita objętość wynosiła : $x^{2}<1-y^{2}$ $z^{2}<1-y^{2}$ ${\ Displaystyle 2 {\ sqrt {1-y ^ {2}}}}$

{\ Displaystyle \ Displaystyle \ int _ {-1} ^ {1} 4 (1-y ^ {2}) \, Dy.}

I to jest ta sama całka jak w poprzednim przykładzie. Jan Hogendijk twierdzi, że oprócz objętości bicylindra Archimedes znał jego powierzchnię , co jest również racjonalne.

Inne propozycje w palimpseście

Szereg twierdzeń geometrii dowodzą w palimpseście podobne argumenty. Jedno z twierdzeń mówi, że położenie środka masy półkuli znajduje się 5/8 drogi od bieguna do środka kuli. Ten problem jest godny uwagi, ponieważ ocenia całkę sześcienną.

Languages

In other projects