Immersja (matematyka) - Immersion (mathematics)

Butelki Klein , zanurzone w przestrzeni 3-wymiarowej.

W matematyce An zanurzeniowy jest różniczkowalną funkcją między rozmaitość różniczkowa której pochodną jest wszędzie pomocą wstrzyknięć . Wyraźnie f  : M → N jest immersją, jeśli

${\ Displaystyle D_ {p} f: T_ {p} M \ do T_ {f (p)} N \,}$

jest funkcją injektywną w każdym punkcie p z M (gdzie T _p X oznacza przestrzeń styczną rozmaitości X w punkcie p w X ). Równoważnie f jest immersją, jeśli jej pochodna ma stałą rangę równą wymiarowi M :

${\ Displaystyle \ operatorname {ranga} \, D_ {p} f = \ dim M.}$

Sama funkcja f nie musi być iniektywna, musi być tylko jej pochodna.

Pokrewnym pojęciem jest osadzenie . Gładkie osadzenie to iniektywne zanurzenie f  : M → N , które jest również zanurzeniem topologicznym , tak że M jest dyfeomorficzne z obrazem w N . Zanurzenie jest dokładnie zanurzeniem lokalnym – tj. dla dowolnego punktu x ∈ M istnieje sąsiedztwo , U ⊆ M , x takie, że f  : U → N jest zanurzeniem i odwrotnie, zanurzenie lokalne jest zanurzeniem. W przypadku rozmaitości nieskończenie wymiarowych czasami przyjmuje się, że jest to definicja zanurzenia.

Rozmaitość zanurzona iniekcyjnie, która nie jest osadzeniem.

Jeśli M jest zwarte , immersja iniektywna jest osadzeniem, ale jeśli M nie jest zwarta, to immersje iniektywne nie muszą być osadzeniami; porównaj do ciągłych bijekcji kontra homeomorfizmy .

Zwykła homotopia

Regularne homotopią dwóch zanurzenia, f i g z a kolektorem M do kolektora N definiuje się różniczkowalną funkcją H  : K x [0,1] → N , że dla wszystkich t w [0, 1], funkcję H _t  : M → N określa H _t ( x ) = H ( x , t ) dla każdego x ∈ M jest zanurzenie z H ₀ = f , H ₁ = g . Homotopia zwykła jest zatem homotopią poprzez immersję.

Klasyfikacja

Hassler Whitneya inicjowane systematyczne badanie zanurzeń i regularne homotopies w 1940, co dowodzi, że do 2 m < n + 1 co mapę f  : M ^m → N ⁿ o m -wymiarowego kolektora An n -wymiarowej kolektora homotopijne do zanurzenia , aw rzeczywistości do osadzenia dla 2 m < n ; są to twierdzenie Whitneya o zanurzeniu i twierdzenie Whitneya o osadzeniu .

Stephen Smale wyraził regularne klasy homotopii immersji f  : M ^m → R ⁿ jako grupy homotopii pewnej rozmaitości Stiefela . Sfera wywinięcie była szczególnie uderzająca konsekwencja.

Morris Hirsch uogólnił wyrażenie Smale'a do opisu teorii homotopii regularnych klas homotopii zanurzeń dowolnej m- wymiarowej rozmaitości M ^m w dowolnej n- wymiarowej rozmaitości N ⁿ .

Klasyfikację immersji Hirscha-Smale'a uogólnił Michaił Gromow .

Istnienie

Taśmy Möbiusa nie zanurza się w codimension 0, ponieważ jego styczna wiązka nie jest trywialne.

Podstawowym utrudnienia istnienia zanurzenie ı  : M ^m → R ⁿ jest stabilny normalny pakiet z M , jak wykryto jej charakterystycznych klas , a zwłaszcza z klas Stiefel-Whitneya . Oznacza to, że od R ⁿ jest parallelizable , pullback jego wiązka styczna do M jest trywialne ponieważ to wycofywanie jest bezpośrednią sumą (wewnętrznie zdefiniowanej) wiązki stycznej na M , TM , która ma wymiar m , oraz normalnej wiązki ν zanurzenia i , która ma wymiar n − m , aby istniał współwymiar k zanurzenia M , musi istnieć wiązka wektorowa o wymiarze k , ξ ^k , zastępująca wiązkę normalną ν , taką, że TM ⊕ ξ ^k jest trywialna. Odwrotnie, przy takiej wiązce, zanurzenie M z tą wiązką normalną jest równoważne zanurzeniu w miarze 0 całkowitej przestrzeni tej wiązki, która jest rozmaitością otwartą.

Stabilna wiązka normalna jest klasą wiązek normalnych plus wiązek trywialnych, a zatem jeśli stabilna wiązka normalna ma wymiar kohomologiczny k , nie może pochodzić z (niestabilnej) normalnej wiązki o wymiarze mniejszym niż k . Tak więc wymiar kohomologiczny stabilnego normalnego pęczka, wykryty przez jego najwyższą klasę nieznikających cech, jest przeszkodą dla zanurzeń.

Ponieważ klasy charakterystyczne mnożą się pod sumą prostą wiązek wektorowych, przeszkodę tę można określić samoistnie w kategoriach przestrzeni M i jej wiązki stycznej oraz algebry kohomologii. Przeszkodę tę (w kategoriach wiązki stycznej, nie stabilnej normalnej) stwierdził Whitney.

Na przykład wstęga Möbiusa ma nietrywialną wiązkę styczną, więc nie może zanurzyć się w kowymiarze 0 (w R ² ), chociaż osadza się w symetrycznym 1 (w R ³ ).

William S. Massey  ( 1960 ) wykazał, że te charakterystyczne klasy (klasy Stiefela-Whitneya stabilnej wiązki normalnej) znikają powyżej stopnia n - α ( n ) , gdzie α ( n ) jest liczbą cyfr "1", gdy n jest napisany w formacie binarnym; ta granica jest ostra, jak urzeczywistnia rzeczywista przestrzeń projekcyjna . To dało dowód na hipotezę o zanurzeniu , a mianowicie, że każdy n- rozmaitość może być zanurzony w kowymiarze n − α ( n ) , tj. w R ^{2 n −α( n )} . Przypuszczenie to potwierdził Ralph Cohen  ( 1985 ).

Współwymiar 0

Codimension 0 Zanurzenia są równoważnie względny wymiar 0 zanurzenia i są lepiej traktowane jako zanurzenia. Zanurzenie w kowymiarze 0 zamkniętej rozmaitości jest dokładnie mapą pokrycia , tj. wiązką włókien z 0-wymiarowym (dyskretnym) włóknem. Zgodnie z twierdzeniem Ehresmanna i twierdzeniem Phillipsa o zanurzeniach, prawidłowe zanurzenie rozmaitości to wiązka włókien, stąd współwymiar/wymiar względny 0 zanurzenia/zanurzenia zachowują się jak zanurzenia.

Co więcej, immersje w koledimieniu 0 nie zachowują się jak inne immersje, które są w dużej mierze zdeterminowane przez stabilną wiązkę normalną: w kodymimencie 0 mamy do czynienia z zagadnieniami dotyczącymi podstawowych przestrzeni klas i pokrycia. Na przykład nie ma miareczkowania 0 zanurzenia S ¹ → R ¹ , mimo że okrąg jest paralelizowalny, co można udowodnić, ponieważ linia nie ma klasy podstawowej, więc nie otrzymujemy wymaganej mapy na górnej kohomologii. Alternatywnie dzieje się to przez niezmienność domeny . Podobnie, chociaż S ³ i 3-torus T ³ można zrównoleglić, nie ma zanurzenia T ³ → S ³ – każda taka osłona musiałaby być rozgałęziona w niektórych punktach, ponieważ sfera jest po prostu połączona.

Innym sposobem zrozumienia tego jest to, że miara k zanurzenia rozmaitości odpowiada zanurzeniu w korelacji 0 k- wymiarowej wiązki wektorowej, która jest rozmaitością otwartą, jeśli miara jest większa od 0, ale rozmaitości zamkniętej w miarerze 0 ( jeśli oryginalny kolektor jest zamknięty).

Wiele punktów

Punkt k- krotny (podwójny, potrójny itd.) zanurzenia f  : M → N jest nieuporządkowanym zbiorem { x ₁ , ..., x _k } odrębnych punktów x _i ∈ M o tym samym obrazie f ( x _i ) ∈ N . Jeśli M jest rozmaitością m- wymiarową, a N jest rozmaitością n- wymiarową, to dla immersji f  : M → N w pozycji ogólnej zbiór k -punktów jest rozmaitością ( n − k ( n − m )) -wymiarową . Każde osadzenie jest zanurzeniem bez wielu punktów (gdzie k > 1 ). Zauważ jednak, że odwrotność jest fałszywa: istnieją immersyjne immersje, które nie są osadzeniami.

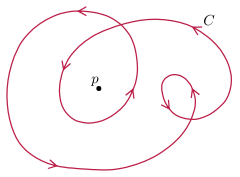
Charakter wielu punktów klasyfikuje zanurzenia; na przykład zanurzenia koła w płaszczyźnie są klasyfikowane do homotopii regularnej przez liczbę podwójnych punktów.

W kluczowym etapie teorii operacji konieczne jest podjęcie decyzji, czy zanurzenie f  : S ^m → N ^{2 m} o w m -sphere w 2 m wymiarową kolektor jest regularny homotopijne do wbudowania, w którym to przypadku może być zabity Chirurgia. Ściana związane z F niezmienna ľ ( f ) w iloraz podstawowej grupy pierścienia Z [ π ₁ ( N )], który zlicza podwójnych punktów F w uniwersalnym pokrywy z N . Dla m > 2 , f jest regularnym homotopem do osadzania wtedy i tylko wtedy, gdy μ ( f ) = 0 przez trik Whitneya .

Osadzenia można badać jako „zanurzenia bez wielu punktów”, ponieważ zanurzenia są łatwiejsze do sklasyfikowania. Można więc zacząć od immersji i spróbować wyeliminować wiele punktów, sprawdzając, czy da się to zrobić bez wprowadzania innych osobliwości – badając „wielokrotne alternatywy”. Po raz pierwszy zrobił to André Haefliger , a podejście to jest owocne w przypadku 3 lub więcej kowymiaru – z punktu widzenia teorii chirurgii jest to „wysoki (ko)wymiar”, w przeciwieństwie do kowymiaru 2, który jest wymiarem węzła, jak w przypadku węzła teoria . Jest on kategorycznie badany za pomocą „ rachunku funktorów ” Thomasa Goodwillie , Johna Kleina i Michaela S. Weissa .

Przykłady i właściwości

Krzywa czterolistna , 4-petaled róża.

• Róża matematyczna z k płatkami to zanurzenie koła w płaszczyźnie z pojedynczym punktem k- krotki; k może być dowolną liczbą nieparzystą, ale jeśli parzysta musi być wielokrotnością 4, więc cyfra 8 nie jest różą.
• Butelki Klein i wszystkie inne niż orientowanych zamknięte powierzchnie, mogą być zanurzone w przestrzeni 3-wymiarowej, ale nie są osadzone.
• Zgodnie z twierdzeniem Whitneya-Grausteina regularne klasy homotopii zanurzeń okręgu w płaszczyźnie są klasyfikowane przez liczbę uzwojeń , która jest również liczbą punktów podwójnych liczonych algebraicznie (tzn. ze znakami).
• Kula może być obracany wewnątrz na zewnątrz : standardowy osadzania f ₀  : S ² → R ³ jest związana z M ₊₁ = - f ₀  : S ² → R ³ regularną homotopii z zanurzeń f _t  : S ² → R ³ .
• Powierzchnia chłopca to zanurzenie rzeczywistej płaszczyzny rzutowej w 3 przestrzeni; a zatem również zanurzenie sfery 2 do 1.
• Powierzchnia Morin to zanurzenie kuli; zarówno ono, jak i powierzchnia Boya powstają jako modele pośrednie w wywróceniu kuli.

• 

  Powierzchnia chłopca

• 

  Powierzchnia Morin

Zanurzone krzywe płaszczyzny

Ta krzywa ma całkowitą krzywiznę  6 π i skręt numer  3, chociaż ma tylko uzwojenie numer  2 o  p .

Krzywe w płaszczyźnie zanurzonej mają dobrze określoną liczbę skrętów , którą można zdefiniować jako całkowitą krzywiznę podzieloną przez 2 π . Jest to niezmienne w regularnej homotopii, według twierdzenia Whitneya-Grausteina – topologicznie jest to stopień odwzorowania Gaussa lub równoważnie liczba nawinięć stycznej jednostkowej (która nie znika) o pochodzeniu. Co więcej, jest to kompletny zestaw niezmienników – dowolne dwie płaskie krzywe o tej samej liczbie skrętów są regularnymi homotopiami.

Każda krzywa zanurzonej płaszczyzny unosi się do wbudowanej krzywej przestrzennej poprzez oddzielenie punktów przecięcia, co nie jest prawdą w wyższych wymiarach. Po dodaniu danych (które pasmo znajduje się na górze), krzywe w płaszczyźnie zanurzonej dają diagramy węzłów , które są głównym przedmiotem zainteresowania teorii węzłów . O ile krzywe płaszczyzny zanurzonej, aż do homotopii regularnej, są określane liczbą ich skrętów, o tyle węzły mają bardzo bogatą i złożoną strukturę.

Zanurzone powierzchnie w 3 przestrzeniach

Badanie powierzchni zanurzonych w przestrzeni 3-przestrzennej jest ściśle związane z badaniem powierzchni zawęźlonych (osadzonych) w przestrzeni 4-przestrzennej, przez analogię z teorią diagramów węzłów (krzywe płaszczyzny zanurzonej (2-przestrzeń) jako rzuty krzywych zawęźlonych w przestrzeni 3 -przestrzeń): mając powierzchnię z węzłami w 4 przestrzeniach można ją rzutować na powierzchnię zanurzoną w 3 przestrzeni i odwrotnie, mając powierzchnię zanurzoną w 3 przestrzeni można zapytać, czy unosi się do 4 przestrzeni – jest czy jest to rzut zawęźlonej powierzchni w 4 przestrzeniach? Pozwala to powiązać pytania dotyczące tych obiektów.

Podstawowym wynikiem, w przeciwieństwie do krzywizn płaskich, jest to, że nie każda zanurzona powierzchnia unosi się do powierzchni z węzłami. W niektórych przypadkach przeszkoda jest 2-skrętna, jak w przykładzie Koschorke'a , który jest zanurzoną powierzchnią (utworzoną z 3 pasm Möbiusa, z potrójnym punktem ), która nie podnosi się do powierzchni z węzłami, ale ma podwójną osłonę, która nie wyciąg. Szczegółowa analiza jest podana w Carter i Saito (1998a) , podczas gdy nowsze badanie jest podane w Carter, Kamada i Saito (2004) .

Uogólnienia

Daleko idącym uogólnieniem teorii immersji jest zasada homotopii : warunek immersji (ranga pochodnej to zawsze k ) można traktować jako cząstkową relację różniczkową (PDR), co można określić w kategoriach pochodnych cząstkowych funkcja. Następnie teoria immersji Smale-Hirscha jest wynikiem tego, że sprowadza się to do teorii homotopii, a zasada homotopii podaje ogólne warunki i powody, dla których PDRs należy zredukować do teorii homotopii.

Zobacz też

• Zanurzony kolektor podrzędny
• Zanurzenie izometryczne
• Zalew

Uwagi

Bibliografia

Zewnętrzne linki

• Zanurzenie w Atlasie Rozmaitości
• Zanurzenie rozmaitości w Encyklopedii Matematyki