Rzeczywista płaszczyzna rzutowa - Real projective plane

Podstawowym wielokąt na płaszczyźnie rzutowej.	Pasek Möbiusa z pojedynczą krawędzią można zamknąć w płaszczyźnie rzutowej, sklejając ze sobą przeciwległe otwarte krawędzie.	Dla porównania butelka Kleina to pasek Möbiusa zamknięty w cylindrze.

W matematyce The rzeczywistym rzutowa płaszczyzna jest przykładem zwartej non orientowanego dwuwymiarowego kolektora ; innymi słowy jednostronna powierzchnia . Nie może być osadzony w standardowej trójwymiarowej przestrzeni bez przecinania się. Ma podstawowe zastosowania w geometrii , ponieważ powszechną konstrukcją rzeczywistej płaszczyzny rzutowej jest przestrzeń linii w R ³ przechodzących przez początek układu współrzędnych.

Płaszczyzna jest również często opisywana topologicznie, w kategoriach konstrukcji opartej na pasku Möbiusa : gdyby można było przykleić (pojedynczą) krawędź paska Möbiusa do siebie we właściwym kierunku, otrzymalibyśmy płaszczyznę rzutową. (Nie można tego zrobić w przestrzeni trójwymiarowej bez powierzchni przecinającej się.) Równoważnie przyklejenie dysku wzdłuż granicy paska Möbiusa daje płaszczyznę rzutową. Topologicznie ma cechę Eulera 1, stąd demigenus (rodzaj nieorientowalny , rodzaj Eulera) równy 1.

Ponieważ pasek Möbiusa z kolei może być skonstruowany z kwadratu przez sklejenie dwóch jego boków razem, rzeczywista płaszczyzna rzutowa może być zatem reprezentowana jako kwadrat jednostkowy (czyli [0, 1] × [0,1] ) z jego stronami zidentyfikowanymi przez następujące relacje równoważności :

(0, y ) ~ (1, 1 − y ) dla 0 ≤ y ≤ 1

i

( x , 0) ~ (1 − x , 1) dla 0 ≤ x ≤ 1,

jak na diagramie po lewej stronie pokazanym tutaj.

Przykłady

Geometria rzutowa niekoniecznie dotyczy krzywizny, a rzeczywista płaszczyzna rzutowa może być skręcona i umieszczona w płaszczyźnie euklidesowej lub w przestrzeni 3 na wiele różnych sposobów. Niektóre z ważniejszych przykładów zostały opisane poniżej.

Płaszczyzna rzutowa nie może być osadzona (czyli bez przecięcia) w trójwymiarowej przestrzeni euklidesowej . Dowód na to, że płaszczyzna rzutowa nie zanurza się w trójwymiarowej przestrzeni euklidesowej, brzmi następująco: Zakładając, że zanurza się, ograniczyłby zwarty obszar w trójwymiarowej przestrzeni euklidesowej przez uogólnione twierdzenie o krzywej Jordana . Pole wektora normalnego skierowanego na zewnątrz dałoby wtedy orientację rozmaitości brzegowej, ale rozmaitość brzegowa byłaby płaszczyzną rzutową , która nie jest orientowalna. Jest to sprzeczność, a więc nasze założenie, że to się zawiera, musiało być fałszywe.

Sfera projekcyjna

Rozważmy sferę i niech jej wielkie okręgi będą „liniami”, a pary antypodów niech będą „punktami”. Łatwo sprawdzić, czy ten system jest zgodny z aksjomatami wymaganymi dla płaszczyzny rzutowej :

każda para odrębnych wielkich kręgów spotyka się w parze antypodów; i
dowolne dwie odrębne pary antypodów leżą na jednym wielkim okręgu.

Jeśli zidentyfikujemy każdy punkt na sferze z jego antypodalnym punktem, to otrzymamy reprezentację rzeczywistej płaszczyzny rzutowej, w której „punkty” płaszczyzny rzutowej rzeczywiście są punktami. Oznacza to, że płaszczyzna rzutowa jest przestrzenią ilorazową kuli uzyskaną przez podział kuli na klasy równoważności w relacji równoważności ~, gdzie x ~ y jeśli y = x lub y = −x. Ta ilorazowa przestrzeń sfery jest homeomorficzna ze zbiorem wszystkich linii przechodzących przez początek w R ³ .

Mapa ilorazowa z kuli na rzeczywistą płaszczyznę rzutową jest w rzeczywistości dwuwarstwową (tj. dwa do jednego) mapą pokrywającą . Wynika z tego, że podstawową grupą rzeczywistej płaszczyzny rzutowej jest grupa cykliczna rzędu 2; czyli liczby całkowite modulo 2. Można wziąć pętlę AB z powyższego rysunku za generator.

Półkula projekcyjna

Ponieważ kula dwukrotnie pokrywa rzeczywistą płaszczyznę rzutową, płaszczyzna może być reprezentowana jako zamknięta półkula, wokół której przeciwległe punkty są podobnie identyfikowane.

Powierzchnia chłopca – immersja

Płaszczyzna rzutowa może być zanurzona (lokalne sąsiedztwa przestrzeni źródłowej nie posiadają samoprzecięć) w przestrzeni 3-przestrzennej. Powierzchnia chłopca jest przykładem immersji.

Przykłady wielościenne muszą mieć co najmniej dziewięć twarzy.

Rzymska powierzchnia

Animacja powierzchni rzymskiej

Powierzchnia rzymska Steinera jest bardziej zdegenerowaną mapą płaszczyzny rzutowej na 3 przestrzeń, zawierającą krzyżyk .

Tetrahemihexahedron jest wielościanów reprezentacja rzeczywistej płaszczyzny rzutowej.

Wielościanów reprezentacja jest tetrahemihexahedron , który ma taką samą formę jak ogólny Steinera Roman powierzchni, pokazanym tutaj.

Hemi wielościany

Patrząc w przeciwnym kierunku, pewne abstrakcyjne wielościany regularne – półsześcian , pół-dwunastościan i pół- dwudziestościan – mogą być skonstruowane jako regularne figury w płaszczyźnie rzutowej; zobacz także wielościany rzutowe .

Rzuty planarne

Opisano różne rzuty płaskie (płaskie) lub odwzorowania płaszczyzny rzutowej. W 1874 Klein opisał mapowanie:

{\ Displaystyle k (x, y) = \ lewo (1 + x ^ {2} + Y ^ {2} \ prawej) ^ {\ Frac {1} {2}} {\ zacząć {pmatrix} x \ \ y \end{pmacierz}}}

Rzut centralny półkuli rzutowej na płaszczyznę daje zwykłą nieskończoną płaszczyznę rzutową, opisaną poniżej.

Dysk krzyżowy

Zamkniętą powierzchnię uzyskuje się poprzez przyklejenie krążka do nasadki krzyżowej . Tę powierzchnię można przedstawić parametrycznie za pomocą następujących równań:

{\ Displaystyle {\ zacząć {wyrównany} X (u, v) i = r \ (1+ \ cos v) \ \ cos u \ \ Y (u, v) & = r \ (1+ \ cos v)\,\sin u,\\Z(u,v)&=-\operatorname {tanh} \left(u-\pi \right)\,r\,\sin v,\end{aligned}} }

gdzie u i v mieszczą się w zakresie od 0 do 2 π .

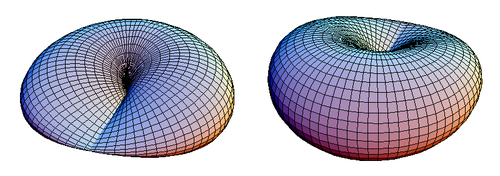
Te równania są podobne do równań torusa . Rysunek 1 przedstawia zamknięty dysk z nasadką krzyżową.

Rysunek 1. Dwa widoki dysku z nakładkami krzyżowymi.

Dysk o nasadce krzyżowej ma płaszczyznę symetrii, która przechodzi przez jego odcinek linii złożony z podwójnych punktów. Na rysunku 1 dysk o nasadce krzyżowej jest widoczny z góry płaszczyzny symetrii z = 0, ale wyglądałby tak samo, gdyby był widziany od dołu.

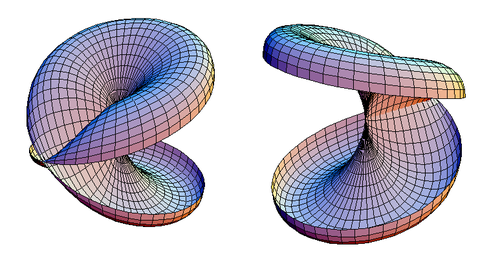
Dysk z nasadką krzyżową można rozciąć wzdłuż płaszczyzny symetrii, uważając, aby nie przeciąć żadnego z jego podwójnych punktów. Wynik pokazano na rysunku 2.

Rysunek 2. Dwa widoki dysku zakorkowanego krzyżowo, który został rozcięty.

Po zrobieniu tego wyjątku widać, że pocięty krążek o krzyżowej nasadce jest homeomorficzny z krążkiem samoprzecinającym się, jak pokazano na rysunku 3.

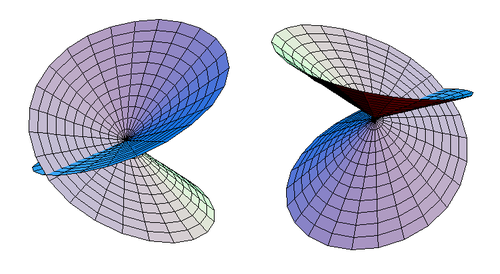
Rysunek 3. Dwa alternatywne widoki samoprzecinającego się dysku.

Dysk samoprzecinający się jest homeomorficzny ze zwykłym dyskiem. Równania parametryczne dysku samoprzecinającego się to:

{\ Displaystyle {\ zacząć {wyrównane} X (u, v) i = r \ v \ \ cos 2u \ \ Y (u, v) i = r \ v \ \ sin 2u \ \ Z (u,v)&=r\,v\,\cos u,\end{wyrównany}}}

gdzie u wynosi od 0 do 2 π, a v od 0 do 1.

Rzutując samoprzecinający się dysk na płaszczyznę symetrii ( z = 0 w podanej wcześniej parametryzacji), która przechodzi tylko przez podwójne punkty, otrzymujemy zwykły dysk, który się powtarza (podwaja się).

Płaszczyzna z = 0 tnie samoprzecinający się dysk na parę dysków, które są swoimi lustrzanymi odbiciami . Dyski mają centra na początku .

Rozważmy teraz felgi dysków (przy v = 1). Punkty na obrzeżu samoprzecinającego się dysku występują parami, które są odbiciami od siebie względem płaszczyzny z = 0.

Dysk z nasadką krzyżową jest tworzony przez identyfikację tych par punktów, dzięki czemu są one sobie równoważne. Oznacza to, że punkt o parametrach ( u , 1) i współrzędnych jest utożsamiany z punktem ( u + π, 1) o współrzędnych . Oznacza to jednak, że pary przeciwległych punktów na obrzeżu (równoważnego) zwykłego dysku są ze sobą utożsamiane; w ten sposób z dysku powstaje prawdziwa płaszczyzna rzutowa. Dlatego powierzchnia pokazana na Figurze 1 (przekrój nasadki z dysku) jest równoważne topologicznie rzeczywistej płaszczyzny rzutowej RP ² . $(r\,\cos 2u,r\,\sin 2u,r\,\cos u)$ $(r\,\cos 2u,r\,\sin 2u,-r\,\cos u)$

Jednorodne współrzędne

Punkty na płaszczyźnie mogą być reprezentowane przez jednorodne współrzędne . Punkt ma jednorodne współrzędne [ x : y : z ] , gdzie współrzędne [ x : y : z ] i [ tx : ty : tz ] są uważane za reprezentujące ten sam punkt, dla wszystkich niezerowych wartości t . Punkty o współrzędnych [ x : y :1] to zwykła płaszczyzna rzeczywista , zwana skończoną częścią płaszczyzny rzutowej, a punkty o współrzędnych [ x : y :0], zwane punktami w nieskończoności lub punktami idealnymi , tworzą prostą zwaną linii w nieskończoności . (Jednorodne współrzędne [0 : 0 : 0] nie reprezentują żadnego punktu.)

Linie na płaszczyźnie mogą być również reprezentowane przez jednorodne współrzędne. Linia rzutowa odpowiadająca płaszczyźnie ax + przez + cz = 0 w R ³ ma jednorodne współrzędne ( a : b : c ). Zatem współrzędne te mają relację równoważności ( a : b : c ) = ( da : db : dc ) dla wszystkich niezerowych wartości d . Stąd inny równanie samej linii DAX + dby + DCz = 0 daje takie same współrzędne jednorodne. Punkt [ x : y : z ] leży na prostej ( a : b : c ) jeśli ax + przez + cz = 0. Zatem proste o współrzędnych ( a : b : c ) gdzie a , b nie są równe 0 odpowiadają do linii w zwykłej rzeczywistej płaszczyźnie , ponieważ zawierają punkty, które nie są w nieskończoności. Linia o współrzędnych (0 : 0 : 1) jest linią w nieskończoności, ponieważ jedynymi punktami na niej są te o z = 0.

Punkty, linie i płaszczyzny

Linia w P ² można przedstawić równaniem ax + o + CZ = 0. Jeżeli leczenia się , b i c, jak w kolumnie do wektora £ -l , a X , Y , Z , ponieważ wektor kolumna x to powyższe równanie może być zapisany w formie macierzowej jako:

x ^Tℓ = 0 lub ℓ ^Tx = 0.

Używając notacji wektorowej, możemy zamiast tego napisać x ⋅ ℓ = 0 lub ℓ ⋅ x = 0.

Równanie k ( x ^Tℓ ) = 0 (które k jest niezerowym skalarem) wymiata płaszczyznę, która przechodzi przez zero w R ^3, a k ( x ) wymiata linię, ponownie przechodząc przez zero. Płaszczyzna i prosta są liniowymi podprzestrzeniami w R ³ , które zawsze przechodzą przez zero.

Punkty idealne

W P ² równanie prostej to ax + przez + cz = 0 i równanie to może reprezentować prostą na dowolnej płaszczyźnie równoległej do płaszczyzny x , y przez pomnożenie równania przez k .

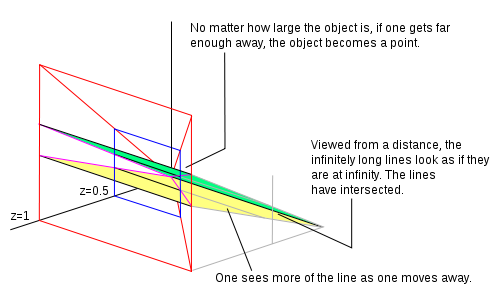
Jeśli z = 1 mamy znormalizowaną współrzędną jednorodną. Wszystkie punkty, które mają z = 1 tworzą płaszczyznę. Załóżmy, że patrzymy na tę płaszczyznę (z miejsca położonego dalej wzdłuż osi z i patrząc wstecz w kierunku początku) i na płaszczyźnie narysowane są dwie równoległe linie. Z miejsca, w którym stoimy (biorąc pod uwagę nasze możliwości wzrokowe) widzimy tylko tyle płaszczyzny, którą przedstawiamy jako obszar zaznaczony na schemacie na czerwono. Jeśli odejdziemy od płaszczyzny wzdłuż osi z (wciąż patrząc wstecz w kierunku początku), możemy zobaczyć więcej płaszczyzny. W naszym polu widzenia oryginalne punkty przesunęły się. Możemy odzwierciedlić ten ruch, dzieląc jednorodną współrzędną przez stałą. Na sąsiednim obrazku podzieliliśmy przez 2, więc wartość z wynosi teraz 0,5. Jeśli odejdziemy wystarczająco daleko, to, na co patrzymy, staje się punktem w oddali. Odchodząc, widzimy coraz więcej równoległych linii. Linie spotkają się na linii w nieskończoności (linia, która przechodzi przez zero na płaszczyźnie w z = 0 ). Linie na płaszczyźnie, gdy z = 0 są punktami idealnymi. Płaszczyzna w z = 0 jest linią w nieskończoności.

Punkt jednorodny (0, 0, 0) to miejsce, w którym idą wszystkie rzeczywiste punkty, gdy patrzysz na płaszczyznę z nieskończonej odległości, linia na płaszczyźnie z = 0 to miejsce, w którym przecinają się równoległe linie.

Dwoistość

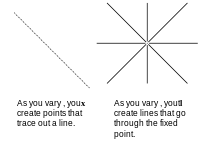
W równaniu x ^Tℓ = 0 występują dwa wektory kolumnowe . Możesz zachować jedną stałą i zmieniać drugą. Jeśli utrzymamy stały punkt x i zmienimy współczynniki ℓ , utworzymy nowe linie przechodzące przez ten punkt. Jeśli utrzymujemy stałe współczynniki i zmieniamy punkty, które spełniają równanie, tworzymy linię. Traktujemy x jako punkt, ponieważ osie, których używamy, to x , y i z . Gdybyśmy zamiast tego wykreślili współczynniki za pomocą osi oznaczonych a , b , c punkty stałyby się liniami, a linie stałyby się punktami. Jeśli udowodnisz coś z danymi wykreślonymi na osiach oznaczonych x , y i z , ten sam argument może zostać użyty dla danych wykreślonych na osiach oznaczonych a , b i c . To jest dualizm.

Linie łączące punkty i przecięcia linii (przy użyciu dualności)

Równanie x ^Tℓ = 0 oblicza iloczyn skalarny dwóch wektorów kolumnowych. Iloczyn skalarny dwóch wektorów wynosi zero, jeśli wektory są ortogonalne . W P ² linia pomiędzy punktami x ₁ i x ₂ może być reprezentowana jako wektor kolumnowy ℓ spełniający równania x ₁^Tℓ = 0 i x ₂^Tℓ = 0 lub innymi słowy wektor kolumnowy ℓ , który jest prostopadły do x ₁ i x ₂ . Produkt przekroju znajdzie taki wektor: linia łączenia dwóch punktów współrzędnych jednorodnych się równaniem x ₁ x x ₂ . Przecięcie dwóch prostych można znaleźć w ten sam sposób, używając dualności, jako iloczyn poprzeczny wektorów reprezentujących proste, ℓ ₁ × ℓ ₂ .

Osadzanie w 4-wymiarowej przestrzeni

Płaszczyzna rzutowa zanurza się w 4-wymiarowej przestrzeni euklidesowej. Rzeczywista płaszczyzna rzutowa P ² ( R ) jest ilorazem dwóch sfer

S ² = {( x , y , z ) ∈ R ³ : x ² + y ² + z ² = 1}

przez relację antypodalną ( x , y , z ) ~ ( − x , − y , − z ) . Rozważ funkcję R ³ → R ⁴ daną przez ( x , y , z ) ↦ ( xy , xz , y ² − z ² , 2 yz ) . To odwzorowanie ogranicza się do odwzorowania, którego domeną jest S ^{2 ,} a ponieważ każdy składnik jest jednorodnym wielomianem parzystego stopnia, przyjmuje te same wartości w R ⁴ na każdym z dwóch antypodów na S ² . Daje to odwzorowanie P ² ( R ) → R ⁴ . Co więcej, ta mapa jest osadzeniem. Zauważ, że to osadzenie dopuszcza rzut na R ^{3 ,} który jest powierzchnią rzymską .

Wyższe powierzchnie bez orientacji

Sklejając kolejno płaszczyzny rzutowe otrzymujemy nieorientowalne powierzchnie wyższego półgenu . Proces klejenia polega na wycięciu małego krążka z każdej powierzchni i zidentyfikowaniu ( sklejeniu ) ich okręgów granicznych. Sklejenie dwóch rzutowych płaszczyzn tworzy butelkę Kleina .

Artykuł o podstawowym wieloboku opisuje wyższe powierzchnie nieorientowalne.

Zobacz też

Bibliografia

Coxeter, HSM (1955), The Real Projective Plane , wyd. Cambridge: W wydawnictwie uniwersyteckim.
Reinhold Baer, Algebra liniowa i geometria rzutowa , Dover, 2005 ( ISBN 0-486-44565-8 )
Richter, David A., Dwa modele rzeczywistej płaszczyzny rzutowej , pobrane 15.04.2010

Languages

In other projects