Dodatek Minkowskiego - Minkowski addition
W geometrii The suma Minkowskiego (znany również jako rozszerzenie ) dwóch zestawów z wektorów pozycji A i B w przestrzeni euklidesowej jest utworzony przez dodanie każdego wektora w A do każdego wektora w B , to jest zestaw
Analogicznie różnicę Minkowskiego (lub różnicę geometryczną) definiuje się za pomocą operacji dopełnienia jako
Ogólnie . Na przykład w przypadku jednowymiarowym i różnicy Minkowskiego , natomiast
W przypadku dwuwymiarowym różnica Minkowskiego jest ściśle związana z erozją (morfologią) w przetwarzaniu obrazu .
Koncepcja nosi imię Hermanna Minkowskiego .
Przykład
Na przykład, jeśli mamy dwa zbiory A i B , każdy składający się z trzech wektorów położenia (nieformalnie trzech punktów), reprezentujących wierzchołki dwóch trójkątów w , o współrzędnych
i
to ich suma Minkowskiego wynosi
który zawiera wierzchołki sześciokąta.
Dla dodania Minkowskiego zbiór zer , zawierający tylko wektor zerowy , 0, jest elementem identyczności : dla każdego podzbioru S przestrzeni wektorowej,
Zbiór pusty jest ważne Minkowskiego Ponadto, ponieważ pusty zestaw niszczy co drugi podzbiór: dla każdego podzbioru S w przestrzeni wektorowej, ich suma z pustego zestawu jest puste:
Jako inny przykład rozważ sumy Minkowskiego otwartych lub zamkniętych kul w polu, które są albo liczbami rzeczywistymi albo liczbami zespolonymi Jeśli jest kulą zamkniętą o promieniu o środku w to dla dowolnego i będzie również obowiązywać dla dowolnego skalara tak że iloczyn jest zdefiniowane (co dzieje się, gdy lub ). Jeśli i wszystkie są niezerowe, to te same równości nadal by były zdefiniowane jako otwarta kula, a nie zamknięta kula, wyśrodkowana (założenie niezerowe jest potrzebne, ponieważ otwarta kula o promieniu jest zbiorem pustym) . Suma Minkowskiego kuli zamkniętej i kuli otwartej jest kulą otwartą. Bardziej ogólnie, suma Minkowskiego podzbioru otwartego z dowolnym innym zbiorem będzie podzbiorem otwartym.
Jeśli jest wykres z , a jeśli i to -działający w czym suma Minkowskiego tych dwóch zamkniętych podzbiorów płaszczyzny jest otwarty zestaw składający się z wszystkiego innego niż -działający. To pokazuje, że suma Minkowskiego dwóch zbiorów domkniętych niekoniecznie jest zbiorem domkniętym. Jednak suma Minkowskiego dwóch zamkniętych podzbiorów będzie podzbiorem domkniętym, jeśli przynajmniej jeden z tych zbiorów jest również podzbiorem zwartym .
Wypukłe łuski sum Minkowskiego
Dodatek Minkowskiego dobrze zachowuje się w odniesieniu do operacji przyjmowania łusek wypukłych , o czym świadczy następująca propozycja:
- Dla wszystkich niepustych podzbiorów i rzeczywistej przestrzeni wektorowej powłoka wypukła ich sum Minkowskiego jest sumą Minkowskiego ich powłok wypukłych:
Ten wynik jest bardziej ogólny dla każdego skończonego zbioru niepustych zbiorów:
W terminologii matematycznej operacje sumowania Minkowskiego i formowania wypukłych kadłubów są operacjami przemiennymi .
Jeśli jest zbiorem wypukłym, to także jest zbiorem wypukłym; Ponadto
dla każdego . I odwrotnie, jeśli ta „ własność rozdzielcza ” obowiązuje dla wszystkich nieujemnych liczb rzeczywistych , to zbiór jest wypukły.
Rysunek po prawej pokazuje przykład zestawu niewypukłego, dla którego
Przykładem w wymiarze jest: Można to łatwo obliczyć, ale stąd znowu
Sumy Minkowskiego działają liniowo na obwodzie dwuwymiarowych ciał wypukłych: obwód sumy jest równy sumie obwodów. Dodatkowo, jeśli jest (wnętrzem) krzywą o stałej szerokości , to suma Minkowskiego i jej obrotu jest dyskiem. Te dwa fakty można połączyć, aby uzyskać krótki dowód twierdzenia Barbiera o obwodzie krzywych o stałej szerokości.
Aplikacje
Dodatek Minkowskiego odgrywa kluczową rolę w morfologii matematycznej . Powstaje w szczotki i udaru paradygmacie z 2D grafiki komputerowej (z różnych zastosowań, w szczególności przez Donald E. Knuth w mEtaFoNt-a ), jak i w stałych przemiatania operacji komputerowych 3D grafiki . Wykazano również, że jest ściśle powiązany z odległością poruszacza Ziemi , a co za tym idzie, optymalnym transportem .
Planowanie ruchu
Sumy Minkowskiego wykorzystywane są w planowaniu ruchu obiektu wśród przeszkód. Służą do obliczania przestrzeni konfiguracyjnej , która jest zbiorem wszystkich dopuszczalnych pozycji obiektu. W prostym modelu ruchu postępowego obiektu w płaszczyźnie, w którym położenie obiektu może być jednoznacznie określone położeniem stałego punktu tego obiektu, przestrzenią konfiguracyjną jest suma Minkowskiego zbioru przeszkód i ruchomego obiekt umieszczony w początku i obrócony o 180 stopni.
Obróbka numeryczna (NC)
W obróbce sterowanej numerycznie programowanie narzędzia NC wykorzystuje fakt, że suma Minkowskiego elementu skrawanego wraz z jego trajektorią daje kształt nacięcia w materiale.
Modelowanie brył 3D
W OpenSCAD Minkowski sumy są używane do obrysowania kształtu innym kształtem, tworząc połączenie obu kształtów.
Teoria agregacji
Sumy Minkowskiego są również często stosowane w teorii agregacji, gdy poszczególne obiekty, które mają zostać zagregowane, są charakteryzowane za pomocą zbiorów.
Wykrywanie kolizji
Sumy Minkowskiego, a konkretnie różnice Minkowskiego, są często używane wraz z algorytmami GJK do obliczania wykrywania kolizji dla wypukłych kadłubów w silnikach fizycznych .
Algorytmy obliczania sum Minkowskiego

Przypadek planarny
Dwa wypukłe wielokąty na płaszczyźnie
Dla dwóch wypukłych wielokątów P i Q w płaszczyźnie o m i n wierzchołkach ich suma Minkowskiego jest wielokątem wypukłym o co najwyżej m + n wierzchołkach i może być obliczona w czasie O( m + n ) za pomocą bardzo prostej procedury, która może być nieformalnie opisany w następujący sposób. Załóżmy, że podane są krawędzie wielokąta i kierunek, powiedzmy, przeciwny do ruchu wskazówek zegara, wzdłuż granicy wielokąta. Wtedy łatwo zauważyć, że te krawędzie wielokąta wypukłego są uporządkowane według kąta biegunowego . Połączmy uporządkowane sekwencje skierowanych krawędzi z P i Q w jeden uporządkowany ciąg S . Wyobraź sobie, że te krawędzie to solidne strzałki, które można swobodnie przesuwać, utrzymując je równolegle do pierwotnego kierunku. Połącz te strzały w kolejności sekwencji S , dołączając ogon następnej strzały do grotu poprzedniej strzały. Okazuje się, że otrzymany łańcuch wielokątny będzie w rzeczywistości wielokątem wypukłym, który jest sumą Minkowskiego P i Q .
Inny
Jeśli jeden wielokąt jest wypukły, a drugi nie, złożoność ich sumy Minkowskiego wynosi O(nm). Jeśli oba są niewypukłe, ich złożoność sumy Minkowskiego wynosi O((mn) 2 ).
Niezbędna suma Minkowskiego
Istnieje również pojęcie zasadniczej sumy Minkowskiego + e dwóch podzbiorów przestrzeni euklidesowej. Zwykłą sumę Minkowskiego można zapisać jako
Zatem zasadnicza suma Minkowskiego jest zdefiniowana przez:
gdzie μ oznacza n- wymiarową miarę Lebesgue'a . Powodem terminu „niezbędny” jest następująca właściwość funkcji wskaźnika : while
można zauważyć, że
gdzie "ess sup" oznacza zasadnicze supremum .
Suma L p Minkowskiego
Dla zwartych podzbiorów wypukłych K i L w , sumę Minkowskiego można opisać funkcją wsparcia zbiorów wypukłych:
Dla p ≥ 1 , Firey zdefiniował sumę L p Minkowskiego K + p L zwartych zbiorów wypukłych K i L w zawierających pochodzenie jako
Dzięki nierówności Minkowskiego funkcja h K+ p L jest znowu dodatnio jednorodna i wypukła, a zatem jest funkcją podporową zwartego zbioru wypukłego. Definicja ta ma podstawowe znaczenie w L p teorii Brunn-Minkowskiego.
Zobacz też
- Suma Blaschke
- Twierdzenie Brunna –Minkowskiego , nierówność na objętości sum Minkowskiego
- Skręt
- Rozszerzanie się
- Erozja
- Arytmetyka interwałowa
- Objętość mieszana (inaczej Quermassintegral lub objętość wewnętrzna )
- Krzywa równoległa
- Lemat Shapleya-Folkmana
- Sumset
- Topologiczna przestrzeń wektorowa#Właściwości
- Zonotop
Uwagi
- ^ Hadwiger, Hugo (1950), "Dodawanie i odejmowanie Minkowskich beliebiger Punktmengen und die Theoreme von Erhard Schmidt", Math. Z. , 53 (3): 210–218, doi : 10.1007/BF01175656
- ^ Twierdzenie 3 (strony 562-563): Krein, M .; Šmulian, V. (1940). „Na regularnie wypukłych zestawach w przestrzeni sprzężone z przestrzenią Banacha”. Roczniki Matematyki . Druga seria. 41 . s. 556-583. doi : 10.2307/1968735 . JSTOR 1968735 . MR 0002009 .
- ^ Dla przemienności dodawania Minkowskiego i wypukłości , patrz Twierdzenie 1.1.2 (strony 2-3) w Schneider; odniesienie to omawia znaczną część literatury na temat wypukłych łusek sumsetów Minkowskiegow „Rozdziale 3 Dodatek Minkowskiego” (strony 126-196): Schneider, Rolf (1993). Ciała wypukłe: Teoria Brunna-Minkowskiego . Encyklopedia matematyki i jej zastosowania. 44 . Cambridge: Wydawnictwo Uniwersytetu Cambridge. s. XIV+490. Numer ISBN 978-0-521-35220-8. MR 1216521 .
- ^ Rozdział 1: Schneider Rolf (1993). Ciała wypukłe: Teoria Brunna-Minkowskiego . Encyklopedia matematyki i jej zastosowania. 44 . Cambridge: Wydawnictwo Uniwersytetu Cambridge. s. XIV+490. Numer ISBN 978-0-521-35220-8. MR 1216521 .
- ^ Twierdzenie Barbiera (Java) na przecięciu węzła .
- ^ Kline, Jeffery (2019). „Właściwości d-wymiarowego problemu poruszania ziemi”. Dyskretna matematyka stosowana . 265 : 128–141. doi : 10.1016/j.dam.2019.02.042 .
- ^ Zelenyuk, V (2015). „Agregacja wydajności wagi” . Europejski Dziennik Badań Operacyjnych . 240 (1): 269–277. doi : 10.1016/j.ejor.2014.06.038 .
- ^ Mayer, A.; Zelenyuk, V. (2014). „Agregacja wskaźników produktywności Malmquista pozwalająca na realokację zasobów” . Europejski Dziennik Badań Operacyjnych . 238 (3): 774–785. doi : 10.1016/j.ejor.2014.04.003 .
- ^ Firey, William J. (1962), „ p- średnie ciał wypukłych”, Math. Skanowanie. , 10 : 17–24, doi : 10.7146/math.scand.a-10510
Bibliografia
- Arrow, Kenneth J .; Hahn, Frank H. (1980). Ogólna analiza konkurencji . Zaawansowane podręczniki z ekonomii. 12 (przedruk (1971) San Francisco, CA: Holden-Day, Inc. Teksty z ekonomii matematycznej. 6 wyd.). Amsterdam: Holandia Północna. Numer ISBN 978-0-444-85497-1. MR 0439057 .
- Gardner, Richard J. (2002), "Nierówność Brunna-Minkowskiego", Bull. Amer. Matematyka. Soc. (NS) , 39 (3): 355–405 (elektroniczny), doi : 10.1090/S0273-0979-02-00941-2
- Zielony, Jerry; Heller, Walter P. (1981). „1 Analiza matematyczna i wypukłość z zastosowaniami w ekonomii”. W Arrow, Kenneth Joseph ; Intryligator, Michael D (red.). Podręcznik ekonomii matematycznej, Tom I. Podręczniki z ekonomii. 1 . Amsterdam: North-Holland Publishing Co. s. 15-52. doi : 10.1016/S1573-4382(81)01005-9 . Numer ISBN 978-0-444-86126-9. Numer MR 0634800 .
- Henry Mann (1976), Twierdzenia o dodawaniu: Twierdzenia o dodawaniu teorii grup i teorii liczb (poprawiony przedruk z 1965 Wiley ed.), Huntington, New York: Robert E. Krieger Publishing Company, ISBN 978-0-88275-418-5– przez http://www.krieger-publishing.com/subcats/MathematicsandStatistics/mathematicsandstatistics.html
- Rockafellar, R. Tyrrell (1997). Analiza wypukła . Zabytki Princeton w matematyce (Przedruk z serii matematycznej Princeton z 1979 r., 28 ed.). Princeton, NJ: Princeton University Press. s. xviii+451. Numer ISBN 978-0-691-01586-6. MR 1451876 .
- Nathanson, Melvyn B. (1996), Teoria liczb addytywnych: problemy odwrotne i geometria sum , GTM, 165 , Springer, Zbl 0859.11003.
- Oks, Edwardzie; Sharir, Micha (2006), "Minkowski Sums of Monotone and General Simple Polygons", Geometria dyskretna i obliczeniowa , 35 (2): 223-240, doi : 10.1007/s00454-005-1206-y.
- Schneider, Rolf (1993), Ciała wypukłe: teoria Brunna-Minkowskiego , Cambridge: Cambridge University Press.
- Tao, Terence & Vu, Van (2006), Additive Combinatorics , Cambridge University Press.
- Mayer, A.; Zelenyuk, V. (2014). „Agregacja wskaźników produktywności Malmquista pozwalająca na realokację zasobów” . Europejski Dziennik Badań Operacyjnych . 238 (3): 774–785. doi : 10.1016/j.ejor.2014.04.003 .
- Zelenyuk, V (2015). „Agregacja wydajności wagi” . Europejski Dziennik Badań Operacyjnych . 240 (1): 269–277. doi : 10.1016/j.ejor.2014.06.038 .
Linki zewnętrzne
- „Dodatek Minkowskiego” , Encyklopedia Matematyki , EMS Press , 2001 [1994]
- Howe, Roger (1979), O tendencji do wypukłości sumy wektorowej zbiorów , Cowles Foundation discussion papers, 538 , Cowles Foundation for Research in Economics , Yale University
- Sumy Minkowskiego , w bibliotece algorytmów geometrii obliczeniowej
- Suma Minkowskiego dwóch trójkątów i Suma Minkowskiego dysku i wielokąta autorstwa George'a Becka, Projekt Wolfram Demonstrations .
- Dodatek Minkowskiego wypukłych kształtów autorstwa Aleksandra Bogomolnego : aplet
- Wikibooks: Podręcznik użytkownika OpenSCAD/Transformacje#minkowski autorstwa Mariusa Kintela: Aplikacja
- Zastosowanie dodatku Minkowskiego do robotyki Joan Gerard





![{\displaystyle A=[-2,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbb3b2c35beab902e541c06decf5cc3c5927108c)
![{\displaystyle B=[-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fb6d50ed2578716b08499727541b3c1158b92cd)
![{\displaystyle AB=[-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ceac3d392f986dc9d4e4bef20194c5474bf39cd)
![{\ Displaystyle A + (-B) = A + B = [-3,3].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cba8aaab0b445dad6fff3e8ecd62824f5f130203)
![W nieujemnej ćwiartce płaszczyzny kartezjańskiej pokazano trzy kwadraty. Kwadrat Q1=[0,1]×[0,1] jest zielony. Kwadrat Q2=[1,2]×[1,2] jest brązowy i znajduje się wewnątrz turkusowego kwadratu Q1+Q2=[1,3]×[1,3].](https://upload.wikimedia.org/wikipedia/commons/thumb/3/3e/Minkowski_sum_graph_-_vector_version.svg/220px-Minkowski_sum_graph_-_vector_version.svg.png)
![{\displaystyle Q_{1}=[0,1]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c158e566e222dca2be8edd3ecc63b4966998e55f)
![{\displaystyle Q_{2}=[1,2]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2878ef1dd56e18f76a6260d3a8c7c712680ec0b8)
![{\displaystyle Q_{1}+Q_{2}=[1,3]^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c66543a4635b0640b76274a1e9f7bd39ac0372b8)














![{\displaystyle r\w [0,\infty]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/affd500e943a70b77bcf1d1fec2ac33ebd40cbec)


![{\displaystyle r,s\in [0,\infty],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23a99aea0187c3e4dfcc541bd266795b20cfccd0)
























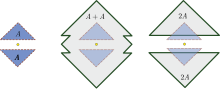



![{\ Displaystyle B = [1,2] \ filiżanka [4,5].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2ddfc83d6354c47f38c91dbb850040e7aab26da)
![{\ Displaystyle 2B = [2,4] \ filiżanka [8,10]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ca2d21ec745d26f46559130715bc7537e5a0457)
![{\ Displaystyle B + B = [2,4] \ filiżanka [5,7] \ filiżanka [8,10],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d25bcdd6b95ca928868a11c947d06e5451cca71)




![{\ Displaystyle A + _ {\ operatorname {e}} B = \ lewo \ {z \ w \ mathbb {R} ^ {n} \, | \ \ mu \ lewo [A \ czapka (zB) \ prawo] >0\prawo\},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9af5c9f57284f12fc7554946cef9d094f065578)




