Grupa Heisenberga - Heisenberg group

W matematyce The grupa Heisenberga , nazwany Werner Heisenberga , jest grupa 3 x 3 górnych trójkątnych macierzy o postaci ${\ Displaystyle H}$

${\displaystyle {\rozpocząć{pmatrix}1&a&c\\0&1&b\\0&0&1\\\koniec {pmatrix}}}$

w ramach operacji mnożenia macierzy . Elementy a, b i c mogą być pobrane z dowolnego pierścienia przemiennego o identyczności, często uważanego za pierścień liczb rzeczywistych (co daje w wyniku „ciągłą grupę Heisenberga”) lub pierścień liczb całkowitych (co daje w wyniku „dyskretną grupę Heisenberga”) .

Ciągła grupa Heisenberga pojawia się w opisie jednowymiarowych układów mechaniki kwantowej , zwłaszcza w kontekście twierdzenia Stone-von Neumanna . Bardziej ogólnie, można rozważyć grupy Heisenberga związane z układami n- wymiarowymi, a najogólniej z dowolną symplektyczną przestrzenią wektorową .

Sprawa trójwymiarowa

W przypadku trójwymiarowym iloczyn dwóch macierzy Heisenberga jest określony wzorem:

${\ Displaystyle {\ zacząć {pmatrix} 1&a&c\\0&1&b\\0&0&1\\\koniec {pmatrix}}{\zacząć {pmatrix} 1&a'&c'\\0&1&b'\\0&0&1\\\end {pmatrix}}= {\begin{pmatrix}1&a+a'&c+ab'+c'\\0&1&b+b'\\0&0&1\\\end{pmatrix}}\,.}$

Jak widać z terminu ab' , grupa jest nieabelowa .

Neutralnym elementem grupy Heisenberga jest macierz jednostkowa , a odwrotności dane przez

${\ Displaystyle {\ zacząć {pmatrix} 1&a&c\\0&1&b\\0&0&1\\\koniec {pmatrix}}^{-1}={\zacząć{pmatrix}1&-a&ab-c\\0&1&-b\\0&0&1\ \\end{pmatrix}}\,.}$

Grupa jest podgrupą dwuwymiarowej grupy afinicznej Aff(2): działanie na odpowiada przekształceniu afinicznym . ${\displaystyle {\rozpocząć{pmatrix}1&a&c\\0&1&b\\0&0&1\\\koniec {pmatrix}}}$${\ Displaystyle ({\ vec {x}}, 1)}$${\ Displaystyle {\ zacząć {pmatrix} 1 & a \ \ 0 i 1 \ koniec {pmatrix}} {\ vec {x}} + {\ zacząć {pmatrix} c \ \ b \ koniec {pmatrix}}}$

Istnieje kilka wybitnych przykładów trójwymiarowego przypadku.

Ciągła grupa Heisenberg

Jeśli a, b, c , są liczbami rzeczywistymi (w pierścieniu R ), to mamy ciągłą grupę Heisenberga H ₃ ( R ).

Jest to nilpotent prawdziwa grupa Lie wymiaru 3.

Oprócz reprezentacji jako rzeczywiste macierze 3x3, ciągła grupa Heisenberga ma również kilka różnych reprezentacji w kategoriach przestrzeni funkcyjnych . Według twierdzenia Stone'a-von Neumanna , aż do izomorfizmu, istnieje unikalna nieredukowalna unitarna reprezentacja H, w której jego centrum działa przez dany nietrywialny charakter . Ta reprezentacja ma kilka ważnych realizacji lub modeli. W modelu Schrödingera grupa Heisenberga działa na przestrzeni funkcji całkowalnych z kwadratem . W reprezentacji theta działa na przestrzeń funkcji holomorficznych na górnej półpłaszczyźnie ; jest tak nazwany ze względu na jego związek z funkcjami theta .

Dyskretna grupa Heisenberg

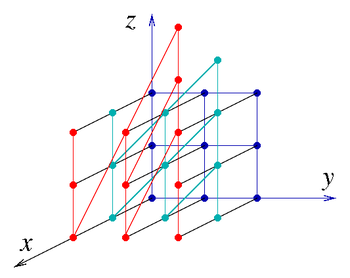
Jeśli a, b, c są liczbami całkowitymi (w pierścieniu Z ), to mamy dyskretną grupę Heisenberga H ₃ ( Z ). Jest to nieabelowa grupa nilpotentów . Posiada dwa generatory,

${\ Displaystyle x = {\ zacząć {pmatrix} 1 i 1 i 0 \ \ 0 i 1 i 0 \ \ 0 i 0 i 1 \ \ \ koniec {pmatrix}}, \ \ y = {\ zacząć {pmatrix} 1 i 0 i 0 \ \ 0 i 1 i 1 \ \ 0 i 0 i 1 \ \ \ koniec {pmatrix }}}$

i relacje

${\ Displaystyle Z_ {} ^ {} = xyx ^ {-1} ^ {-1} \ xz = zx \ yz = zy}$,

gdzie

${\ Displaystyle z = {\ zacząć {pmatrix} 1 i 0 i 1 \ \ 0 i 1 i 0 \ \ 0 i 0 i 1 \ \ \ koniec {pmatrix}}}$

jest generatorem centrum H ₃ . (Zauważ, że odwrotności x , y i z zastępują 1 nad przekątną przez −1.)

Według twierdzenia Bassa ma wielomianowy współczynnik wzrostu rzędu 4.

Można wygenerować dowolny element poprzez

${\ Displaystyle {\ zacząć {pmatrix} 1 i a & c \ \ 0 i 1 i b \ \ 0 i 0 i 1 \ \ \ koniec {pmatrix}} = y ^ {b} z ^ {c} x ^ {a} \}.$

Grupa Heisenberga modulo nieparzysta liczba pierwsza p

Jeśli weźmiemy a, b, c w Z / p Z za nieparzystą liczbę pierwszą p , to mamy grupę Heisenberga modulo p . Jest to grupa rzędu p ³ z generatorami x,y i relacjami:

${\ Displaystyle Z_ {} ^ {} = xyx ^ {-1} y ^ {-1} \ x ^ {p} = y ^ {p} = z ^ {p} = 1 \ xz = zx \ yz=zy.}$

Analogi grup Heisenberga nad ciałami skończonymi nieparzystego pierwszego rzędu p nazywane są grupami ekstra-specjalnymi , lub bardziej poprawnie, grupami ekstra-specjalnymi wykładnika p . Mówiąc bardziej ogólnie, jeśli wyprowadzona podgrupa grupy G jest zawarta w centrum Z grupy G , to odwzorowanie z G/Z × G/Z → Z jest skośno-symetrycznym dwuliniowym operatorem na grupach abelowych.

Jednak wymaganie, aby G/Z było skończoną przestrzenią wektorową, wymaga, aby podgrupa Frattiniego z G była zawarta w środku, a wymaganie, aby Z było jednowymiarową przestrzenią wektorową nad Z / p Z wymaga, aby Z miało porządek p , więc jeśli G nie jest abelowe, to G jest wyjątkowe. Jeśli G jest bardzo szczególne, ale nie ma wykładnika p , to poniższa ogólna konstrukcja zastosowana do symplektycznej przestrzeni wektorów G/Z nie daje grupy izomorficznej z G .

Grupa Heisenberga modulo 2

Grupa Heisenberga modulo 2 jest rzędu 8 i jest izomorficzna z grupą dwuścienną D ₄ (symetrie kwadratu). Zauważ, że jeśli

${\ Displaystyle x = {\ zacząć {pmatrix} 1 i 1 i 0 \ \ 0 i 1 i 0 \ \ 0 i 0 i 1 \ \ \ koniec {pmatrix}}, \ \ y = {\ zacząć {pmatrix} 1 i 0 i 0 \ \ 0 i 1 i 1 \ \ 0 i 0 i 1 \ \ \ koniec {pmatrix }}}$.

Następnie

${\ Displaystyle xy = {\ zacząć {pmatrix} 1 i 1 i 1 \ \ 0 i 1 i 1 \ \ 0 i 0 i 1 \ \ \ koniec {pmatrix}}}$

oraz

${\ Displaystyle yx = {\ zacząć {pmatrix} 1 i 1 i 0 \ \ 0 i 1 i 1 \ \ 0 i 0 i 1 \ \ \ koniec {pmatrix}}.}$

Elementy x i y odpowiadają odbiciom (pomiędzy nimi 45°), natomiast xy i yx odpowiadają obrotom o 90°. Pozostałe odbicia to xyx i yxy , a obrót o 180° to xyxy (= yxyx ).

Algebra Heisenberga

Algebra Liego grupy Heisenberga (na liczbach rzeczywistych) jest znana jako algebra Heisenberga. Jest reprezentowany za pomocą przestrzeni macierzy formy ${\displaystyle {\mathfrak {h}}}$${\ Displaystyle H}$${\displaystyle 3\razy 3}$

${\displaystyle {\rozpocząć{pmatrix}0&a&c\\0&0&b\\0&0&0\\\koniec {pmatrix}}}$,

z . Następujące trzy elementy stanowią podstawę dla : ${\displaystyle a,b,c\in \mathbb {R}}$${\displaystyle {\mathfrak {h}}}$

${\ Displaystyle X = {\ zacząć {pmatrix} 0 i 1 i 0 \ \ 0 i 0 i 0 \ \ 0 i 0 i 0 \ \ \ koniec {pmatrix}}; \ quad Y = {\ zacząć {pmatrix} 0 i 0 i 0 \ \ 0 i 0 i 1 \ \ 0 i 0 i 0 \ \ \ koniec {pmatrix }};\quad Z={\begin{pmatrix}0&0&1\\0&0&0\\0&0&0\\\end{pmatrix}}}$.

Elementy bazowe spełniają relacje komutacyjne:

${\ Displaystyle [X, Y] = Z; \ quad [X, Z] = 0; \ quad [Y, Z] = 0}$.

Nazwa „grupa Heisenberga” jest motywowana poprzednimi relacjami, które mają taką samą postać jak kanoniczne relacje komutacyjne w mechanice kwantowej:

${\ Displaystyle [{\ kapelusz {x}}, {\ kapelusz {p}}] = ja \ hbar ja; \ quad [ {\ kapelusz {x}}, ja \ hbar ja] = 0; \ quad [ {\ kapelusz {p}},i\hbar I]=0}$,

gdzie jest operatorem pozycji, jest operatorem pędu i jest stałą Plancka. ${\displaystyle {\kapelusz {x}}}$${\displaystyle {\kapelusz {p}}}$${\ Displaystyle \ hbar}$

Grupa Heisenberga ma specjalną właściwość polegającą na tym, że odwzorowanie wykładnicze jest odwzorowaniem jeden do jednego i na odwzorowanie z algebry Liego do grupy . ${\ Displaystyle H}$${\displaystyle {\mathfrak {h}}}$${\ Displaystyle H}$

Wyższe wymiary

Bardziej ogólne grupy Heisenberga można zdefiniować dla wyższych wymiarów w przestrzeni euklidesowej, a bardziej ogólnie na symplektycznych przestrzeniach wektorowych . Najprostszym przypadkiem ogólnym jest rzeczywista grupa wymiarów Heisenberga dla dowolnej liczby całkowitej . Jako grupę macierzy (lub w celu wskazania, że ​​jest to grupa Heisenberga nad ciałem liczb rzeczywistych) jest zdefiniowana jako macierze grupowe z wpisami i mające postać: ${\ Displaystyle H_ {2n+1}}$${\displaystyle 2n+1}$${\displaystyle n\geq 1}$${\ Displaystyle H_ {2n+1}}$${\ Displaystyle H_ {2n + 1} (\ mathbb {R})}$${\ Displaystyle \ mathbb {R}}$${\ Displaystyle (n + 2) \ razy (n + 2)}$${\ Displaystyle \ mathbb {R}}$

${\ Displaystyle {\ zacząć {bmatrix} 1 & \ mathbf {a} & c \ \ \ mathbf {0} i_ {n} i \ mathbf {b} \ \ 0 i \ mathbf {0} i 1 \ koniec {bmatrix}}}$

gdzie

a jest wektorem wierszowym o długości n ,

b jest wektorem kolumnowym o długości n ,

Że _brak jest macierzą jednostkową o rozmiarze n .

Struktura grupy

To jest rzeczywiście grupa, jak pokazuje mnożenie:

${\ Displaystyle {\ zacząć {bmatrix} 1 & \ mathbf {a} & c \ \ 0 i ja_ {n} i \ mathbf {b} \ \ 0 i 0 i 1 \ koniec {bmatrix}} \ cdot {\ zacząć {bmatrix} 1 i \ mathbf {a } '&c'\\0&I_{n}&\mathbf {b} '\\0&0&1\end{bmatrix}}={\begin{bmatrix}1&\mathbf {a} +\mathbf {a} '&c+c' +\mathbf {a} \cdot \mathbf {b} '\\0&I_{n}&\mathbf {b} +\mathbf {b} '\\0&0&1\end{bmatrix}}}$

oraz

${\ Displaystyle {\ zacząć {bmatrix} 1 & \ mathbf {a} & c \ \ 0 & I_ {n} i \ mathbf {b} \ \ 0 i 0 i 1 \ koniec {bmatrix}} \ cdot {\ zacząć {bmatrix} 1 & - \ mathbf { a} &-c+\mathbf {a} \cdot \mathbf {b} \\0&I_{n}&-\mathbf {b} \\0&0&1\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&I_ {n}&0\\0&0&1\end{bmatryca}}.}$

Algebra kłamstwa

Grupa Heisenberga jest po prostu połączoną grupą Liego, której algebra Liego składa się z macierzy

${\ Displaystyle {\ zacząć {bmatrix} 0 & \ mathbf {a} & c \ \ 0 i 0_ {n} i \ mathbf {b} \ \ 0 i 0 i 0 \ koniec {bmatrix}}}$

gdzie

a jest wektorem wierszowym o długości n ,

b jest wektorem kolumnowym o długości n ,

0 _n jest macierzą zerową o rozmiarze n .

Niech e ₁ , ..., e _n będzie kanoniczną podstawą R ⁿ , a ustawienie

${\ Displaystyle p_ {i} = {\ zacząć {bmatrix} 0 i \ nazwa operatora {e} _ {i} ^ {\ operator {T}} i 0 \ \ 0 i 0_ {n} i 0 \ \ 0 i 0 i 0 \ koniec {bmatrix}}, }$

${\ Displaystyle q_ {j} = {\ zacznij {bmatrix} 0 i 0 i 0 \ \ 0 i 0_ {n} i \ nazwa operatora {e} _ {j} \ \ 0 i 0 i 0 \ koniec {bmatrix}}}$

${\ Displaystyle z = {\ zacząć {bmatrix} 0 i 0 i 1 \ \ 0 i 0_ {n} i 0 \ \ 0 i 0 i 0 \ koniec {bmatrix}}}$

powiązaną algebra Liego można scharakteryzować za pomocą kanonicznych relacji komutacyjnych ,

${\ Displaystyle {\ zacząć {bmatrix} p_ {i}, q_ {j} \ koniec {bmatrix}}} = \ delta _ {ij} z, \ qquad {\ zacząć {bmatrix} p_ {i}, z \ koniec { bmatryca}}=0,\qquad {\begin{bmatryca}q_{j},z\end{bmatryca}}=0~,}$

(1)

gdzie p ₁ , ...,  p _n , q ₁ , ...,  q _n , z są generatorami algebry.

W szczególności z jest centralnym elementem algebry Heisenberga Liego. Zauważ, że algebra Liego grupy Heisenberga jest nilpotentna.

Mapa wykładnicza

Pozwolić

${\ Displaystyle u = {\ zacząć {bmatrix} 0 i \ mathbf {a} i c \ \ 0 i 0_ {n} i \ mathbf {b} \ \ 0 i 0 i 0 \ koniec {b macierzy}}}$

który spełnia . Wykładniczy mapa ocenia się ${\ Displaystyle u ^ {3} = 0_ {n + 2}}$

${\ Displaystyle \ exp (u) = \ suma _ {k = 0} ^ {\ infty} {\ Frac {1} {k!}} u ^ {k} = ja_ {n + 2} + u + {\ tfrac {1}{2}}u^{2}={\begin{bmatrix}1&\mathbf {a} &c+{1 \over 2}\mathbf {a} \cdot \mathbf {b} \\0&I_{n} &\mathbf {b} \\0&0&1\end{bmacierz}}.}$

Wykładnicza mapa dowolnej nilpotentnej algebry Liego jest dyfeomorfizmem między algebrą Liego a unikalną powiązaną, połączoną , po prostu połączoną grupą Liego.

Ta dyskusja (oprócz stwierdzeń odnoszących się do wymiaru i grupy Liego) ma zastosowanie dalej, jeśli zastąpimy R dowolnym pierścieniem przemiennym A . Odpowiednia grupa jest oznaczona jako H _n ( A ).

Przy dodatkowym założeniu, że liczba pierwsza 2 jest odwracalna w pierścieniu A , zdefiniowano również odwzorowanie wykładnicze, ponieważ redukuje się ono do skończonej sumy i ma postać powyżej (np. A może być pierścieniem Z / p Z z nieparzystą liczbą pierwszą p lub dowolne pole o charakterystyce 0).

Teoria reprezentacji

Teoria unitarnej reprezentacji grupy Heisenberga jest dość prosta – później uogólniona przez teorię Mackeya – i była motywacją jej wprowadzenia do fizyki kwantowej, jak omówiono poniżej.

Dla każdej niezerowej liczbę rzeczywistą , można określić nieredukowalnego jednolitą reprezentację z działającą w przestrzeni Hilberta za pomocą wzoru: ${\ Displaystyle \ hbar}$${\ Displaystyle \ Pi _ {\ hbar}}$${\ Displaystyle H_ {2n+1}}$${\ Displaystyle L ^ {2} (\ mathbb {R} ^ {n})}$

${\ Displaystyle \ lewo [\ Pi _ {\ hbar} {\ zacząć {pmatrix} 1 i \ mathbf {a} i c \ \ 0 i I_ {n} i \ mathbf {b} \ \ 0 i 0 i 1 \ koniec {pmatrix}} \ psi \ prawo](x)=e^{i\hbar c}e^{ib\cdot x}\psi (x+\hbar a)}$

Ta reprezentacja jest znana jako reprezentacja Schrödingera . Motywacją dla tej reprezentacji jest działanie wykładniczych operatorów pozycji i pędu w mechanice kwantowej. Parametr opisuje translacje w przestrzeni pozycji, parametr opisuje translacje w przestrzeni pędów, a parametr podaje ogólny współczynnik fazy. Współczynnik fazowy jest potrzebny do uzyskania grupy operatorów, ponieważ translacje w przestrzeni pozycji i translacje w przestrzeni pędów nie są komutowane. ${\displaystyle a}$${\displaystyle b}$${\displaystyle c}$

Kluczowym wynikiem jest twierdzenie Stone-von Neumann , które stwierdza, że ​​każda (silnie ciągła) nieredukowalna unitarna reprezentacja grupy Heisenberga, w której centrum działa nietrywialnie, jest dla niektórych równoważna . Alternatywnie, że wszystkie są równoważne algebrze Weyla (lub algebrze CCR ) na przestrzeni symplektycznej o wymiarze 2 n . ${\ Displaystyle \ Pi _ {\ hbar}}$${\ Displaystyle \ hbar}$

Ponieważ grupa Heisenberga jest jednowymiarowa centralny rozszerzenie jej nieprzywiedlne unitarne reprezentacje mogą być postrzegane jako niesprowadzalnych jednostkowych rzutowych przedstawień o . Koncepcyjnie podana powyżej reprezentacja stanowi kwantowo-mechaniczny odpowiednik grupy symetrii translacyjnych na klasycznej przestrzeni fazowej, . Już na poziomie klasycznym sugeruje się , że wersja kwantowa jest jedynie rzutową reprezentacją . Hamiltonowskie generatory translacji w przestrzeni fazowej to funkcje położenia i pędu. Rozpiętość tych funkcji nie tworzy jednak algebry Liego pod nawiasem Poissona , ponieważ raczej rozpiętość funkcji położenia i pędu oraz stałych tworzy algebrę Liego pod nawiasem Poissona. Ta algebra Liego jest jednowymiarowym centralnym rozszerzeniem przemiennej algebry Liego , izomorficznej z algebrą Liego grupy Heisenberga. ${\ Displaystyle \ mathbb {R} ^ {2n}}$${\ Displaystyle \ mathbb {R} ^ {2n}}$${\ Displaystyle \ mathbb {R} ^ {2n}}$${\ Displaystyle R ^ {2n}}$${\ Displaystyle \ {x_ {i}, p_ {j} \} = \ delta _ {i, j}.}$${\ Displaystyle \ mathbb {R} ^ {2n}}$

Na symplektycznych przestrzeniach wektorowych

Ogólna abstrakcja grupy Heisenberga jest skonstruowana z dowolnej symplektycznej przestrzeni wektorowej . Na przykład, niech ( V ,ω) będzie skończenie-wymiarową rzeczywistą symplektyczną przestrzenią wektorową (więc ω jest niezdegenerowaną skośnie symetryczną formą dwuliniową na V ). Grupa Heisenberga H( V ) na ( V ,ω) (lub po prostu V dla zwięzłości) jest zbiorem V × R obdarzonym prawem grupowym

${\ Displaystyle (v, t) \ cdot (v ', t') = \ lewo (v + v ', t + t '+ {\ tfrac {1} {2}} \ omega (v, v ') \ Prawidłowy).}$

Grupa Heisenberg jest centralnym rozszerzeniem grupy dodatków V . Tak więc istnieje dokładna sekwencja

${\ Displaystyle 0 \ do \ mathbf {R} \ do H (V) \ do V \ do 0.}$

Każda symplektyczna przestrzeń wektorów dopuszcza bazę Darboux { e _j , f ^k } _{1 ≤ j , k ≤ n} spełniającą ω( e _j , f ^k ) = δ _j ^k i gdzie 2 n jest wymiarem V (wymiar V jest koniecznie nawet). Pod względem tej podstawy każdy wektor rozkłada się jako

${\ Displaystyle v = q ^ {a} \ mathbf {e} _ {a} + p_ {a} \ mathbf {f} ^ {a}.}$

Q i P są kanonicznej sprzężone współrzędnych .

Jeśli { e _j , f ^k } _{1 ≤ j , k ≤ n} jest bazą Darboux dla V , to niech { E } będzie bazą dla R , a { e _j , f ^k , E } _{1 ≤ j , k ≤ n} jest odpowiednią podstawą dla V × R . Wektor w H( V ) jest wtedy dany przez

${\ Displaystyle v = q ^ {a} \ mathbf {e} _ {a} + p_ {a} \ mathbf {f} ^ {a} + TE}$

a prawo grupowe staje się

${\ Displaystyle (p, q, t) \ cdot (p', q', t') = \ lewo (p+p',q+q',t+t'+{\frac {1}{2} }(pq'-p'q)\prawo).}$

Ponieważ podstawową rozmaitością grupy Heisenberga jest przestrzeń liniowa, wektory w algebrze Liego mogą być kanonicznie utożsamiane z wektorami w grupie. Algebra Liego grupy Heisenberga jest dana przez relację komutacyjną

${\ Displaystyle {\ zacząć {bmatrix} (v_ {1}, t_ {1}), (v_ {2}, t_ {2}) \ koniec {bmatrix}} = \ omega (v_ {1}, v_ {2 })}$

lub napisane w oparciu o zasadę Darboux

${\ Displaystyle [\ mathbf {e} _ {a}, \ mathbf {f} ^ {b}] = \ delta _ {a} ^ {b}}$

a wszystkie inne komutatory znikają.

Możliwe jest również zdefiniowanie prawa grupowego w inny sposób, który daje grupę izomorficzną do grupy, którą właśnie zdefiniowaliśmy. Aby uniknąć nieporozumień, użyjemy u zamiast t , więc wektor jest dany przez

${\ Displaystyle v = q ^ {a} \ mathbf {e} _ {a} + p_ {a} \ mathbf {f} ^ {a} + uE}$

a prawo grupowe to

${\displaystyle (p,q,u)\cdot (p',q',u')=(p+p',q+q',u+u'+pq').}$

Element grupy

${\ Displaystyle v = q ^ {a} \ mathbf {e} _ {a} + p_ {a} \ mathbf {f} ^ {a} + uE}$

można wtedy wyrazić jako macierz

${\ Displaystyle {\ zacząć {bmatrix} 1 i p i u \ \ 0 i I_ {n} i q \ \ 0 i 0 i 1 \ koniec {bmatrix}}}$ ,

co daje wierną macierzową reprezentację H( V ). U w tym preparacie jest związana z t w poprzednim preparatu przez tak, że t wartość dla produktu chodzi ${\displaystyle u=t+{\tfrac {1}{2}}pq}$

${\displaystyle u+u'+pq'-{\tfrac {1}{2}}(p+p')(q+q')}$

${\displaystyle =t+{\tfrac {1}{2}}pq+t'+{\tfrac {1}{2}}p'q'+pq'-{\tfrac {1}{2}} (p +p')(q+q')}$

${\displaystyle =t+t'+{\tfrac {1}{2}}(pq'-p'q)}$ ,

jak wcześniej.

Izomorfizm do grupy wykorzystującej górne macierze trójkątne polega na rozkładzie V na bazę Darboux, co sprowadza się do wyboru izomorfizmu V ≅ U ⊕ U *. Chociaż nowe prawo grupowe daje grupę izomorficzną z tą podaną wyżej, grupa z tym prawem jest czasami określana jako spolaryzowana grupa Heisenberga, aby przypomnieć, że to prawo grupowe opiera się na wyborze podstawy (wyborze podprzestrzeni Lagrange'a z V jest polaryzacją ).

Z każdą algebrą Liego istnieje unikatowo połączona , po prostu połączona grupa Liego G . Wszystkie dołączone do grupy należeć do tej samej Algebra oscylować G mają postać G / N , gdzie N jest głównym dyskretnych grupa G . W tym przypadku, środek H ( V ), to R i tylko nieciągłe podgrupami są izomorficzna Z . Zatem H( V )/ Z jest kolejną grupą Liego, która dzieli tę samą algebrę Liego. Warto zauważyć, że ta grupa Liego nie dopuszcza żadnych wiernych reprezentacji skończonych wymiarowo; nie jest izomorficzny z żadną grupą macierzy. Ma jednak dobrze znaną rodzinę nieskończenie wymiarowych reprezentacji unitarnych.

Związek z algebrą Weyla

Algebra Liego grupy Heisenberga została opisana powyżej (1), jako algebra Liego macierzy. Twierdzenie Poincaré-Birkhoffa-Witta stosuje się do określenia uniwersalnej algebry obwieszczenia . Wśród innych właściwości, uniwersalna algebra obwieszczenia jest algebrą asocjacyjną, w którą wpisuje się iniekcyjnie. ${\ Displaystyle {\ mathfrak {h}} _ {n}}$ ${\ Displaystyle U ({\ mathfrak {h}} _ {n})}$${\ Displaystyle {\ mathfrak {h}} _ {n}}$

Według twierdzenia Poincarégo-Birkhoffa-Witta jest to zatem wolna przestrzeń wektorowa generowana przez jednomiany

${\ Displaystyle z ^ {j} p_ {1}^ {k_ {1}} p_ {2} ^ {k_ {2}} \ cdots p_ {n} ^ {k_ {n}} q_ {1} ^ {\ ell _{1}}q_{2}^{\ell _{2}}\cdots q_{n}^{\ell _{n}}~,}$

gdzie wszystkie wykładniki są nieujemne.

W związku z tym składa się z rzeczywistych wielomianów ${\ Displaystyle U ({\ mathfrak {h}} _ {n})}$

${\ Displaystyle \ suma _ {j {\ vec {k}} {\ vec {\ ell}}} c_ {j {\ vec {k}} {\ vec {\ ell}}} \ \, z ^{j}p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{n}^{k_{n}}q_{1}^{\ell _{1 }}q_{2}^{\ell _{2}}\cdots q_{n}^{\ell _{n}}~,}$

z relacjami komutacyjnymi

${\displaystyle p_{k}p_{\ell}=p_{\ell}p_{k}\quad q_{k}q_{\ell}=q_{\ell}q_{k}\quad p_{k }q_{\ell }-q_{\ell }p_{k}=\delta _{k\ell }z,\quad zp_{k}-p_{k}z=0,\quad zq_{k}-q_ {k}z=0~.}$

Algebra jest ściśle związana z algebrą operatorów różniczkowych na ℝ ⁿ ze współczynnikami wielomianowymi, ponieważ każdy taki operator ma unikalną reprezentację w postaci ${\ Displaystyle U ({\ mathfrak {h}} _ {n})}$

${\ Displaystyle P = \ suma _ {{\ vec {k}}, {\ vec {\ ell}}} c_ {{\ vec {k}}} {\ vec {\ ell}}} \ \ \ części _{x_{1}}^{k_{1}}\partial _{x_{2}}^{k_{2}}\cdots \partial _{x_{n}}^{k_{n}}x_{ 1}^{\ell _{1}}x_{2}^{\ell _{2}}\cdots x_{n}^{\ell _{n}}~.}$

Ta algebra nazywa się algebrą Weyla . Z abstrakcyjnego nonsensu wynika, że algebra Weyla W _n jest ilorazem . Jednak jest to również łatwe do zobaczenia bezpośrednio z powyższych reprezentacji; mianowicie. przez mapowanie ${\ Displaystyle U ({\ mathfrak {h}} _ {n})}$

${\ Displaystyle z ^ {j} p_ {1}^ {k_ {1}} p_ {2} ^ {k_ {2}} \ cdots p_ {n} ^ {k_ {n}} q_ {1} ^ {\ ell _{1}}q_{2}^{\ell _{2}}\cdots q_{n}^{\ell _{n}}\,\mapsto \,\partial _{x_{1}}^ {k_{1}}\partial _{x_{2}}^{k_{2}}\cdots \partial _{x_{n}}^{k_{n}}x_{1}^{\ell _{ 1}}x_{2}^{\ell _{2}}\cdots x_{n}^{\ell _{n}}~.}$

Aplikacje

Parametryzacja mechaniki kwantowej Weyla

Aplikacja, która doprowadziła Hermanna Weyla do jednoznacznej realizacji grupy Heisenberga, to pytanie, dlaczego obraz Schrödingera i obraz Heisenberga są fizycznie równoważne. Abstrakcyjnie, powodem jest twierdzenie Stone'a-von Neumanna : istnieje unikalna unitarna reprezentacja z danym działaniem centralnego elementu algebry Liego z , aż do unitarnej równoważności: wszystkie nietrywialne elementy algebry są równoważne zwykłej pozycji i pędowi operatorów.

Tak więc obraz Schrödingera i obraz Heisenberga są równoważne – są po prostu różnymi sposobami realizacji tego zasadniczo unikalnego przedstawienia.

Reprezentacja Theta

Ten sam wynik jednoznaczności wykorzystał David Mumford dla dyskretnych grup Heisenberga w swojej teorii równań definiujących rozmaitości abelowe . Jest to duże uogólnienie podejścia stosowanego w funkcjach eliptycznych Jacobiego , czyli przypadek grupy Heisenberga modulo 2 rzędu 8. Najprostszym przypadkiem jest reprezentacja theta grupy Heisenberga, której przypadek dyskretny daje funkcję theta .

Analiza Fouriera

Grupa Heisenberga występuje również w analizie Fouriera , gdzie jest używana w niektórych sformułowaniach twierdzenia Stone-von Neumann . W tym przypadku grupa Heisenberga może być rozumiana jako działająca w przestrzeni kwadratowej funkcji całkowalnych ; rezultatem jest reprezentacja grup Heisenberga, czasami nazywana reprezentacją Weyla.

Jako rozmaitość pod-Riemanna

Trójwymiarowa grupa Heisenberga H ₃ ( R ) na liczbach rzeczywistych może być również rozumiana jako rozmaitość gładka , a konkretnie prosty przykład rozmaitości pod-Riemanna . Biorąc pod uwagę punkt p =( x , y , z ) w R ³ , zdefiniuj różniczkową 1-formę Θ w tym punkcie jako

${\ Displaystyle \ Theta _ {p} = dz-{\ Frac {1} {2}} \ lewo (xdy-ydx \ prawo).}$

Ta jedna forma należy do wiązki cotangent z R ³ ; to jest,

${\ Displaystyle \ Theta _ {p}: T_ {p} \ mathbf {R} ^ {3} \ do \ mathbf {R}}$

to mapa na wiązce stycznej . Pozwolić

${\ Displaystyle H_ {p} = \ {v \ w T_ {p} \ mathbf {R} ^ {3} \ mid \ Theta _ {p} (v) = 0 \}.}$

Można zauważyć, że H jest subbundle stycznej wiązki T R ³ . Cometric o H jest przez wystającą wektorów w dwuwymiarowej przestrzeni objętej przez wektory, w x i y kierunku. Oznacza to, że dane wektory i w T R ³ , iloczyn skalarny jest przez ${\displaystyle v=(v_{1},v_{2},v_{3})}$${\displaystyle w=(w_{1},w_{2},w_{3})}$

${\ Displaystyle \ langle v, w \ rangle = v_ {1} w_ {1} + v_ {2} w_ {2}.}$

Powstała struktura zamienia H w rozmaitość grupy Heisenberga. Układ ortonormalny na rozmaitości jest określony przez pola wektorowe Liego

${\ Displaystyle X = {\ Frac {\ częściowy} {\ częściowy x}} - {\ Frac {1} {2}} y {\ Frac {\ częściowy} {\ częściowy z}}},}$

${\ Displaystyle Y = {\ Frac {\ częściowy} {\ częściowy y}} + {\ Frac {1} {2}} x {\ Frac {\ częściowy} {\ częściowy z}}},}$

${\ Displaystyle Z = {\ Frac {\ częściowy} {\ częściowy Z}},}$

które spełniają relacje [ X , Y ]= Z oraz [ X , Z ]=[ Y , Z ]=0. Będąc polami wektorowymi Liego, tworzą one lewostronną podstawę działania grupowego. W geodezyjne w płycie są spirale wystające do kół w dwóch wymiarach. To znaczy, jeśli

${\ Displaystyle \ gamma (t) = (x (t), y (t), z (t))}$

jest krzywą geodezyjną, to krzywa jest łukiem koła, oraz ${\displaystyle c(t)=(x(t),y(t))}$

${\ Displaystyle Z (t) = {\ Frac {1} {2}} \ int _ {c} xdy-ydx}$

z całką ograniczoną do płaszczyzny dwuwymiarowej. Oznacza to, że wysokość krzywej jest proporcjonalna do powierzchni okręgu objętego łukiem kołowym , co wynika z twierdzenia Stokesa .

Heisenberg grupa lokalnie zwartej grupy abelowej

Bardziej ogólnie można zdefiniować grupę Heisenberga jako lokalnie zwartą grupę abelową K , wyposażoną w miarę Haara . Taka grupa ma podwójną liczbę Pontrjagin , składającą się ze wszystkich znaków o wartościach ciągłych na K , która jest również lokalnie zwartą grupą abelową, jeśli jest wyposażona w topologię zwarto-otwartą . Grupa Heisenberga związana z lokalnie zwartą grupą abelową K jest podgrupą unitarnej grupy generowanej przez translacje z K i mnożenia przez elementy . ${\ Displaystyle {\ kapelusz {K}}}$${\ Displaystyle U(1)}$${\ Displaystyle L ^ {2} (K)}$${\ Displaystyle {\ kapelusz {K}}}$

Bardziej szczegółowo, przestrzeń Hilberta składa się z całkowalnych do kwadratu funkcji o wartościach zespolonych na K . Tłumaczenia w K tworzą jednolitą reprezentację o K jako operatorów na : ${\ Displaystyle L ^ {2} (K)}$${\displaystyle f}$${\ Displaystyle L ^ {2} (K)}$

${\ Displaystyle (T_ {x} f) (y) = f (x + r)}$

dla . Tak samo wykonaj mnożenia przez znaki: ${\displaystyle x,y\wk}$

${\ Displaystyle (M_ {\ chi} f) (y) = \ chi (y) f (y)}$

dla . Operatorzy ci nie dojeżdżają, a zamiast tego spełniają ${\ Displaystyle \ chi \ w {\ kapelusz {K}}}$

${\ Displaystyle (T_ {x} M_ {\ chi} T_ {x} ^ {-1} M_ {\ chi} ^ {-1} f) (y) = {\ overline {\ chi (x)}} f (y)}$

mnożenie przez liczbę zespoloną o ustalonej jednostce modułu.

Zatem grupa Heisenberga związane z K jest rodzajem centralnego przedłużenie o poprzez dokładną kolejność grup: ${\ Displaystyle H (K)}$${\ Displaystyle K \ razy {\ kapelusz {K}}}$

${\ Displaystyle 1 \ do U (1) \ do H (K) \ do K \ razy {\ kapelusz {K}} \ do 0.}$

Bardziej ogólne grupy Heisenberga są opisane przez 2-kocyle w grupie kohomologicznej . Istnienie dwoistości między i powoduje powstanie kanonicznego kocyklu, ale generalnie są też inne. ${\ Displaystyle H ^ {2} (K, U (1))}$${\ Displaystyle K}$${\ Displaystyle {\ kapelusz {K}}}$

Grupa Heisenberg działa nieredukowalnie na . Rzeczywiście, ciągłe znaki oddzielają punkty, więc każdy unitarny operator, który dojeżdża z nimi, jest mnożnikiem . Ale dojazdy z tłumaczeniami oznaczają, że mnożnik jest stały. ${\ Displaystyle L ^ {2} (K)}$${\ Displaystyle L ^ {2} (K)}$${\ Displaystyle L ^ {\ Infty}}$

Dla grupy Heisenberga obowiązuje wersja twierdzenia Stone-von Neumann , udowodniona przez George'a Mackeya . Transformaty Fouriera jest wyjątkowy intertwiner pomiędzy reprezentacjami i . Zobacz dyskusję w twierdzeniu Stone-von Neumanna # Związek z transformatą Fouriera, aby uzyskać szczegółowe informacje. ${\ Displaystyle H (K)}$${\ Displaystyle L ^ {2} (K)}$${\ Displaystyle L ^ {2} ({\ kapelusz {K}})}$

Zobacz też

• Kanoniczne relacje komutacyjne
• Przekształcenie Wignera-Weyla
• Twierdzenie Stone-von Neumanna
• Reprezentacja projekcyjna

Uwagi

Bibliografia

• Binz, Ernst; Strąki, Sonja (2008). Geometria grup Heisenberga . Amerykańskie Towarzystwo Matematyczne . Numer ISBN 978-0-8218-4495-3.
• Hall, Brian C. (2013), Teoria kwantowa dla matematyków , Teksty magisterskie z matematyki, 267 , Springer, ISBN 978-1461471158
• Hall, Brian C. (2015). Grupy Liego, algebry Liego i reprezentacje: podstawowe wprowadzenie . Teksty magisterskie z matematyki. 222 (druga edycja). Skoczek. Numer ISBN 978-3319134666.
• Howe, Roger (1980). „O roli grupy Heisenberga w analizie harmonicznej” . Biuletyn Amerykańskiego Towarzystwa Matematycznego . 3 (2): 821–843. doi : 10.1090/s0273-0979-1980-14825-9 . MR  0578375 .
• Kirillov, Alexandre A. (2004). „Rozdz. 2: „Reprezentacje i orbity grupy Heisenberga”. Wykłady na temat metody orbity . Amerykańskie Towarzystwo Matematyczne. ISBN 0-8218-3530-0.
• Mackey, George (1976). Teoria grupowych reprezentacji unitarnych . Wykłady w Chicago z matematyki. Wydawnictwo Uniwersytetu Chicago . Numer ISBN 978-0226500522.

Zewnętrzne linki

• Groupprops, The Group Properties Wiki Unitriangular matrix group UT(3,p)