Model Isinga - Ising model

Mechanika statystyczna
Termodynamika Teoria kinetyczna
Statystyki cząstek Twierdzenie o statystyce spinowej Identyczne cząstki Maxwell-Boltzmann Bosego-Einsteina Fermi-Dirac Parastatystyka Statystyki Anyonic Statystyki warkoczy
Zespoły termodynamiczne NVE Microcanonical Kanoniczny NVT µVT Wielki kanoniczny NPH izoentalpowo-izobaryczny NPT izotermiczny–izobaryczny
Modele Debye Einstein Śpiewam Potts
Potencjały Energia wewnętrzna Entalpia Energia swobodna Helmholtza Energia swobodna Gibbsa Wielki potencjał / Darmowa energia Landau
Naukowcy Maxwell Boltzmanna Gibbs Einstein Ehrenfest von Neumann Tołman Debye Fermi Bose
v T mi

Modelu Ising ( / aɪ s ɪ ŋ / ; niemiecki: [iːzɪŋ] ), (lub Lenz-model isinga lub modelu Ising-Lenz ), nazwany fizyków Ernst Ising i Wilhelm Lenz (który opracował go w czasie pobytu w Hamburgu University ), to model matematyczny z ferromagnetyzmu w mechanice statystycznej . Model składa się ze zmiennych dyskretnych, które reprezentują magnetyczne momenty dipolowe „spinów” atomowych, które mogą być w jednym z dwóch stanów (+1 lub -1). Spiny są ułożone na wykresie, zwykle w siatce (gdzie lokalna struktura powtarza się okresowo we wszystkich kierunkach), umożliwiając każdemu spinowi interakcję z sąsiadami. Sąsiednie spiny, które są zgodne, mają niższą energię niż te, które się nie zgadzają; system dąży do najniższej energii, ale ciepło zaburza tę tendencję, stwarzając możliwość różnych faz strukturalnych. Model pozwala na identyfikację przejść fazowych jako uproszczonego modelu rzeczywistości. Dwuwymiarowy kwadratowy model Isinga jest jednym z najprostszych modeli statystycznych pokazujących przejście fazowe .

Model Isinga został wymyślony przez fizyka Wilhelma Lenza  ( 1920 ), który dał go jako problem swojemu uczniowi Ernstowi Isingowi. Jednowymiarowy model Isinga rozwiązał sam Ising (1925) w swojej pracy magisterskiej z 1924 r.; nie ma przejścia fazowego. Dwuwymiarowy model Isinga z kwadratową siatką jest znacznie trudniejszy i został przedstawiony dopiero znacznie później przez Larsa Onsagera  ( 1944 ). Zwykle rozwiązuje się go metodą macierzy transferowej , chociaż istnieją różne podejścia, bardziej związane z kwantową teorią pola .

W wymiarach większych niż cztery przejście fazowe modelu Isinga jest opisane przez teorię pola średniego .

Problem Isinga bez pola zewnętrznego można równoważnie sformułować jako problem maksymalnego cięcia grafu (Max-Cut), który można rozwiązać za pomocą optymalizacji kombinatorycznej .

Definicja

Rozważmy zbiór Λ miejsc sieci, każdy z zestawem sąsiadujących miejsc (np. graf ) tworzących d- wymiarową sieć. Dla każdego miejsca sieci k  ∈ Λ istnieje zmienna dyskretna σ _k taka, że ​​σ _k  ∈ {+1, −1}, reprezentująca spin miejsca. Konfiguracja wirowania , σ = (σ _k ) _{k  ∈ Λ} jest przypisanie wartości wirowania każdej stronie kraty.

Dla dowolnych dwóch sąsiednich miejsc i ,  j  ∈ Λ istnieje interakcja J _ij . Również miejsce j  ∈ Λ ma zewnętrzne pole magnetyczne h _j oddziałujące z nim. Energii z Ď konfiguracji jest przez funkcję Hamiltona

${\ Displaystyle H (\ sigma) = - \ suma _ {\ langle i ~ j \ rangle} J_ {ij} \ sigma _ {i} \ sigma _ {j} - \ mu \ suma _ {j} h_ {j }\sigma _{j},}$

gdzie pierwsza suma jest nad parami sąsiednich spinów (każda para jest liczona raz). Oznaczenie ⟨ ij ⟩ wskazuje, że miejsca i oraz j są najbliższymi sąsiadami. Moment magnetyczny jest przez ľ. Zauważ, że znak w drugim członie powyższego hamiltonianu powinien być w rzeczywistości dodatni, ponieważ moment magnetyczny elektronu jest przeciwny do jego spinu, ale człon ujemny jest używany konwencjonalnie. Prawdopodobieństwo konfiguracja jest przez rozkład Boltzmanna z odwrotności temperatury p ≥ 0:

${\ Displaystyle P_ {\ beta} (\ sigma) = {\ Frac {e ^ {-\ beta H (\ sigma)}} {Z_ {\ beta}}}}$

gdzie β = ( k _B T ) ^-1 , a stała normalizacji

${\ Displaystyle Z_ {\ beta} = \ suma _ {\ sigma} e ^ {-\ beta H (\ sigma)}}$

jest funkcją partycji . Dla funkcji f spinów ("obserwowalnej") oznaczamy przez

${\ Displaystyle \ langle f \ rangle _ {\ beta} = \ suma _ {\ sigma} f (\ sigma) P_ {\ beta} (\ sigma)}$

wartość oczekiwana (średnia) f .

Prawdopodobieństwa konfiguracji P _β (σ) reprezentują prawdopodobieństwo, że (w równowadze) układ znajduje się w stanie o konfiguracji σ.

Dyskusja

Znak minus na każdym członie funkcji hamiltonowskiej H (σ) jest umowny. Stosując tę ​​konwencję znaków, modele Isinga można klasyfikować według znaku interakcji: if, dla pary i ,  j

${\ Displaystyle J_ {ij}> 0}$oddziaływanie nazywa się ferromagnetycznym ,

${\ Displaystyle J_ {ij} <0}$, oddziaływanie nazywa się antyferromagnetycznym ,

${\ Displaystyle J_ {ij} = 0}$, Spiny są noninteracting .

System nazywa się ferromagnetycznym lub antyferromagnetycznym, jeśli wszystkie oddziaływania są ferromagnetyczne lub wszystkie są antyferromagnetyczne. Oryginalne modele Isinga były ferromagnetyczne i nadal często zakłada się, że „model Isinga” oznacza ferromagnetyczny model Isinga.

W ferromagnetycznym modelu Isinga spiny dążą do wyrównania: konfiguracje, w których sąsiednie spiny mają ten sam znak, mają większe prawdopodobieństwo. W modelu antyferromagnetycznym sąsiednie spiny mają zwykle przeciwne znaki.

Konwencja znaku H (σ) wyjaśnia również, w jaki sposób miejsce spinu j oddziałuje z polem zewnętrznym. Mianowicie strona spinu chce zrównać się z polem zewnętrznym. Gdyby:

${\displaystyle h_{j}>0}$, miejsce wirowania j chce ustawić się w kierunku dodatnim,

${\ Displaystyle h_ {j} <0}$, miejsce wirowania j chce ustawić się w kierunku ujemnym,

${\ Displaystyle h_ {j} = 0}$, nie ma żadnego zewnętrznego wpływu na stronę wirowania.

Uproszczenia

Modele Isinga są często badane bez zewnętrznego pola oddziałującego z siecią, czyli h  = 0 dla wszystkich j w sieci Λ. Stosując to uproszczenie, hamiltonian staje się

${\ Displaystyle H (\ sigma) = - \ suma _ {\ langle i ~ j \ rangle} J_ {ij} \ sigma _ {i} \ sigma _ {j}.}$

Gdy pole zewnętrzne jest wszędzie zero, h  = 0, model Isinga jest symetryczny przy zmianie wartości spinu we wszystkich miejscach sieci; pole niezerowe łamie tę symetrię.

Innym powszechnym uproszczeniem jest założenie, że wszyscy najbliżsi sąsiedzi ⟨ ij ⟩ mają taką samą siłę interakcji. Wtedy możemy ustawić J _ij = J dla wszystkich par i ,  j w Λ. W tym przypadku hamiltonian jest dalej uproszczony do

${\ Displaystyle H (\ sigma) = - J \ suma _ {\ langle i ~ j \ rangle} \ sigma _ {i} \ sigma _ {j}.}$

Połączenie z wykresem maksymalnego cięcia

Podzbiór S zbioru wierzchołków V(G) ważonego grafu nieskierowanego G określa podział grafu G na S i jego komplementarny podzbiór G\S. Rozmiar cięcia jest sumą wag krawędzi pomiędzy S i G\S. Maksymalne cięcie wielkość jest co najmniej rozmiar jakiegokolwiek innego kroju, zmieniając S.

Dla modelu Isinga bez pola zewnętrznego na grafie G hamiltonian staje się następującą sumą nad krawędziami grafu E(G)

${\ Displaystyle H (\ sigma) = - \ suma _ {ij \ w E (G)} J_ {ij} \ sigma _ {i} \ sigma _ {j}}$.

Tutaj każdy wierzchołek i wykresu jest stroną spinu, która przyjmuje wartość spinu . Dana konfiguracja spinu dzieli zbiór wierzchołków na dwa zależne podzbiory, te ze spinem w górę i te ze spinem w dół . Oznaczmy przez w -depended zestaw krawędzi łączącej dwie komplementarne podzbiory wierzchołków i . Wielkość cięcia z dwustronnym ważonej nieukierunkowane wykres G można określić jako ${\ Displaystyle \ sigma _ {i} = \ pm 1}$${\displaystyle \sigma}$${\ Displaystyle V (G)}$${\displaystyle \sigma}$${\ Displaystyle V ^ {+}}$${\ Displaystyle V ^ {-}}$${\ Displaystyle \ delta (V ^ {+})}$${\displaystyle \sigma}$${\ Displaystyle V ^ {+}}$${\ Displaystyle V ^ {-}}$ ${\ Displaystyle \ lewo | \ delta (V ^ {+}) \ prawo |}$${\ Displaystyle \ delta (V ^ {+})}$

${\ Displaystyle \ lewo | \ delta (V ^ {+}) \ prawo | = {\ Frac {1} {2}} \ suma _ {ij \ w \ delta (V ^ {+})} W_ {ij} }$,

gdzie oznacza wagę krawędzi, a skala 1/2 jest wprowadzana w celu skompensowania podwójnego liczenia tych samych wag . ${\displaystyle W_{ij}}$${\displaystyle ij}$${\ Displaystyle W_ {ij} = W_ {ji}}$

Tożsamości

${\ Displaystyle {\ zacząć {wyrównany} H (\ sigma) & = - \ suma _ {ij \ w E (V ^ {+})} J_ {ij} - \ suma _ {ij \ w E (V ^ { -})}J_{ij}+\sum _{ij\in \delta (V^{+})}J_{ij}\\&=-\sum _{ij\in E(G)}J_{ij }+2\sum _{ij\in \delta (V^{+})}J_{ij},\end{wyrównany}}}$

gdzie całkowita suma w pierwszym okresie nie zależy od , załóżmy, że minimalizowanie w jest równoznaczne z minimalizowaniem . Zdefiniowanie wagi krawędzi zamienia w ten sposób problem Isinga bez pola zewnętrznego w grafowy problem Max-Cut maksymalizujący rozmiar cięcia , który jest powiązany z hamiltonianem Isinga w następujący sposób: ${\displaystyle \sigma}$${\displaystyle H(\sigma)}$${\displaystyle \sigma}$${\ Displaystyle \ suma _ {ij \ w \ delta (V ^ {+})} J_ {ij}}$${\ Displaystyle W_ {ij} = - J_ {ij}}$${\ Displaystyle \ lewo | \ delta (V ^ {+}) \ prawo |}$

${\ Displaystyle H (\ sigma) = \ suma _ {ij \ w E (G)} W_ {ij} -4 \ lewo | \ delta (V ^ {+}) \ po prawej |.}$

pytania

Znaczna liczba pytań statystycznych dotyczących tego modelu mieści się w granicach dużej liczby spinów:

• Czy w typowej konfiguracji większość spinów wynosi +1 czy -1, czy też są one podzielone równo?
• Jeśli obrót na dowolnej pozycji i wynosi 1, jakie jest prawdopodobieństwo, że obrót na pozycji j również wynosi 1?
• Jeśli zmieni się β , czy zachodzi przejście fazowe?
• Na siatce Λ, jaki jest fraktalny wymiar kształtu dużej gromady spinów +1?

Podstawowe właściwości i historia

Najbardziej badanym przypadkiem modelu Isinga jest ferromagnetyczny model zerowego pola o niezmiennym przesunięciu na d- wymiarowej sieci, a mianowicie Λ =  Z ^d , J _ij  = 1, h  = 0.

W swojej pracy doktorskiej z 1924 r. Ising rozwiązał model dla przypadku d  = 1, który można traktować jako liniową sieć poziomą, w której każde miejsce oddziałuje tylko ze swoim lewym i prawym sąsiadem. W jednym wymiarze rozwiązanie nie dopuszcza przejścia fazowego . Mianowicie, dla dowolnych dodatnich β, korelacje ⟨σ _i σ _j ⟩ zanikają wykładniczo w | ja  −  j |:

${\ Displaystyle \ langle \ sigma _ {i} \ sigma _ {j} \ rangle _ {\ beta} \ leq C \ exp {\ duży (}-c (\ beta) | ij | {\ duży)}}$

a system jest nieuporządkowany. Na podstawie tego wyniku błędnie wywnioskował, że model ten nie wykazuje zachowania fazowego w żadnym wymiarze.

Model Isinga przechodzi przejście fazowe między fazą uporządkowaną i nieuporządkowaną w dwóch lub więcej wymiarach. Mianowicie układ jest nieuporządkowany dla małych β, podczas gdy dla dużych β układ wykazuje porządek ferromagnetyczny:

${\ Displaystyle \ langle \ sigma _ {i} \ sigma _ {j} \ rangle _ {\ beta} \ geq c (\ beta)> 0.}$

Po raz pierwszy udowodnił to Rudolf Peierls w 1936 roku, używając tego, co obecnie nazywa się argumentem Peierlsa .

Model Isinga na dwuwymiarowej siatce kwadratowej bez pola magnetycznego został analitycznie rozwiązany przez Larsa Onsagera  ( 1944 ). Onsager wykazał, że funkcje korelacji i energia swobodna modelu Isinga są określane przez nieoddziałujący fermion sieciowy. Onsager ogłosił wzór na spontaniczne namagnesowanie dla modelu dwuwymiarowego w 1949 roku, ale nie podał wyprowadzenia. Yang (1952) przedstawił pierwszy opublikowany dowód tej formuły, wykorzystując formułę graniczną dla wyznaczników Fredholma , udowodnioną w 1951 r. przez Szegő w bezpośredniej odpowiedzi na pracę Onsagera.

Znaczenie historyczne

Jednym z argumentów Demokryta na poparcie atomizmu było to, że atomy w naturalny sposób wyjaśniają ostre granice faz obserwowane w materiałach, na przykład gdy lód topi się w wodę lub woda zamienia się w parę. Jego pomysł polegał na tym, że małe zmiany właściwości w skali atomowej doprowadzą do dużych zmian w zachowaniu agregatów. Inni wierzyli, że materia jest z natury ciągła, a nie atomowa, i że wielkoskalowe właściwości materii nie dają się zredukować do podstawowych właściwości atomowych.

Podczas gdy prawa wiązania chemicznego wyjaśniały dziewiętnastowiecznym chemikom, że atomy są prawdziwe, wśród fizyków debata trwała do początków XX wieku. Atomiści, w szczególności James Clerk Maxwell i Ludwig Boltzmann , zastosowali sformułowanie Hamiltona dotyczące praw Newtona do dużych układów i odkryli, że statystyczne zachowanie atomów prawidłowo opisuje gazy w temperaturze pokojowej. Jednak klasyczna mechanika statystyczna nie uwzględniała wszystkich właściwości cieczy i ciał stałych ani gazów w niskiej temperaturze.

Po sformułowaniu nowoczesnej mechaniki kwantowej atomizm nie kolidował już z eksperymentem, ale nie doprowadziło to do powszechnej akceptacji mechaniki statystycznej, wykraczającej poza atomizm. Josiah Willard Gibbs dał kompletny formalizm, by odtworzyć prawa termodynamiki z praw mechaniki. Jednak wiele błędnych argumentów przetrwało z XIX wieku, kiedy mechanikę statystyczną uważano za wątpliwą. Błędy w intuicji wynikały głównie z faktu, że granica nieskończonego systemu statystycznego ma wiele praw zero-jedynkowych, których nie ma w systemach skończonych: nieskończenie mała zmiana parametru może prowadzić do dużych różnic w ogólnym, zagregowanym zachowaniu, jak Demokryt oczekiwany.

Brak przejść fazowych w skończonej objętości

Na początku XX wieku niektórzy uważali, że funkcja podziału nigdy nie może opisać przejścia fazowego, opierając się na następującym argumencie:

1. Funkcja podziału jest sumą e ^{−β E} we wszystkich konfiguracjach.
2. Funkcja wykładnicza jest wszędzie analityczna jako funkcja β.
3. Suma funkcji analitycznych jest funkcją analityczną.

Argument ten działa dla skończonej sumy wykładników i prawidłowo ustala, że ​​nie ma osobliwości w energii swobodnej układu o skończonych rozmiarach. Dla systemów, które znajdują się w granicy termodynamicznej (czyli dla systemów nieskończonych) nieskończona suma może prowadzić do osobliwości. Konwergencja do granicy termodynamicznej jest szybka, tak że zachowanie fazowe jest widoczne już na stosunkowo małej sieci, nawet jeśli osobliwości są wygładzone przez skończony rozmiar układu.

Zostało to po raz pierwszy ustalone przez Rudolfa Peierlsa w modelu Isinga.

Kropelki Peierlsa

Krótko po tym, jak Lenz i Ising skonstruowali model Isinga, Peierls był w stanie jednoznacznie wykazać, że przejście fazowe zachodzi w dwóch wymiarach.

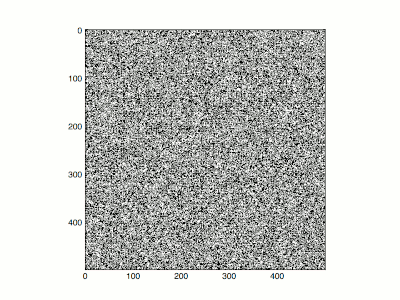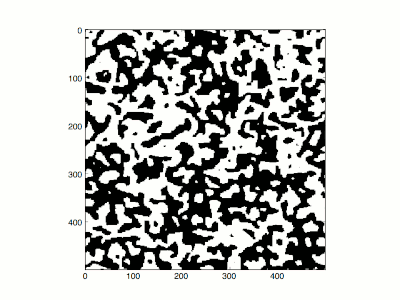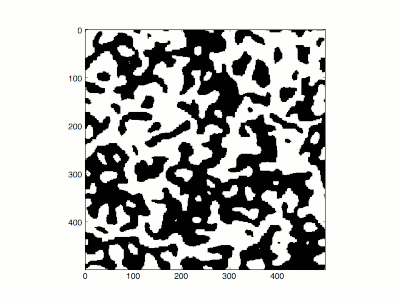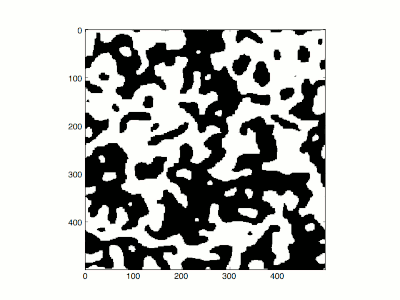
Aby to zrobić, porównał limity wysokiej i niskiej temperatury. W nieskończonej temperaturze (β = 0) wszystkie konfiguracje mają jednakowe prawdopodobieństwo. Każdy spin jest całkowicie niezależny od innych, a jeśli wykreśli się typowe konfiguracje w nieskończonej temperaturze, tak że plus/minus są reprezentowane przez czerń i biel, wyglądają jak telewizyjny śnieg . W przypadku wysokiej, ale nie nieskończonej temperatury, istnieją małe korelacje między sąsiednimi pozycjami, śnieg ma tendencję do zbijania się w grudki, ale ekran pozostaje losowo wyglądający i nie ma nadmiaru czerni lub bieli netto.

Ilościową miarą nadmiaru jest magnetyzacja , która jest średnią wartością spinu:

${\ Displaystyle M = {\ Frac {1} {N}} \ suma _ {i = 1} ^ {N} \ sigma _ {i}.}$

Fałszywy argument analogiczny do argumentu w ostatniej sekcji ustala teraz, że namagnesowanie w modelu Isinga jest zawsze zerowe.

1. Każda konfiguracja spinów ma taką samą energię jak konfiguracja z odwróconymi wszystkimi spinami.
2. Tak więc dla każdej konfiguracji z namagnesowaniem M istnieje konfiguracja z namagnesowaniem − M z równym prawdopodobieństwem.
3. System powinien więc spędzać tyle samo czasu w konfiguracji z namagnesowaniem M jak z namagnesowaniem − M .
4. Tak więc średnie namagnesowanie (przez cały czas) wynosi zero.

Tak jak poprzednio, to tylko dowodzi, że średnie namagnesowanie wynosi zero przy dowolnej skończonej objętości. W przypadku systemu nieskończonego fluktuacje mogą nie być w stanie przesunąć systemu ze stanu głównie plus do stanu głównie minus z niezerowym prawdopodobieństwem.

W przypadku bardzo wysokich temperatur namagnesowanie wynosi zero, tak jak w nieskończonej temperaturze. Aby to zobaczyć, zauważ, że jeśli spin A ma tylko niewielką korelację ε ze spinem B, a B jest tylko słabo skorelowany z C, ale C jest poza tym niezależne od A, wielkość korelacji A i C wygląda jak ε ² . Dla dwóch spinów oddzielonych odległością L , wielkość korelacji wynosi ε ^L , ale jeśli istnieje więcej niż jedna ścieżka, którą mogą podróżować korelacje, wartość ta jest zwiększana o liczbę ścieżek.

Liczba ścieżek o długości L na siatce kwadratowej w wymiarach d wynosi

${\ Displaystyle N (L) = (2d) ^ {L}}$

ponieważ są 2 d możliwości wyboru, gdzie iść na każdym kroku.

Granica całkowitej korelacji jest określona przez wkład do korelacji przez zsumowanie wszystkich ścieżek łączących dwa punkty, które są ograniczone powyżej sumą wszystkich ścieżek o długości L podzieloną przez

${\ Displaystyle \ suma _ {L} (2d) ^ {L} \ varepsilon ^ {L}}$

który spada do zera, gdy ε jest małe.

W niskich temperaturach (β ≫ 1) konfiguracje są bliskie konfiguracji o najniższej energii, takiej, w której wszystkie spiny są plusem lub wszystkie spiny są minusem. Peierls zapytał, czy jest statystycznie możliwe w niskiej temperaturze, zaczynając od wszystkich obrotów minus, do stanu, w którym większość obrotów jest na plus. Aby tak się stało, kropelki wirowania dodatniego muszą być w stanie zastygnąć, aby uzyskać stan dodatni.

Energia kropelki o dodatnich obrotach na ujemnym tle jest proporcjonalna do obwodu kropli L, gdzie dodatnie obroty i ujemne obroty sąsiadują ze sobą. W przypadku kropli o obwodzie L , obszar znajduje się gdzieś pomiędzy ( L  − 2)/2 (linia prosta) a ( L / 4) ² (prostokąt). Koszt prawdopodobieństwa wprowadzenia kropli ma współczynnik e ^{−β L} , ale wpływa to na funkcję podziału pomnożoną przez całkowitą liczbę kropel o obwodzie L , która jest mniejsza niż całkowita liczba dróg o długości L :

${\ Displaystyle N (L) <4 ^ {2L}.}$

Tak więc całkowity udział wirowania z kropelek, nawet przeliczany przez umożliwienie każdemu miejscu posiadania oddzielnej kropelki, jest ograniczony powyżej przez

${\ Displaystyle \ suma _ {L} L ^ {2} 4 ^ {2 L} e ^ {-4 \ beta L}}$

który idzie do zera na dużej β. Dla β wystarczająco dużych, to wykładniczo tłumi długie pętle, tak że nie mogą wystąpić, a namagnesowanie nigdy nie waha się zbyt daleko od -1.

Tak więc Peierls ustalił, że namagnesowanie w modelu Isinga ostatecznie definiuje sektory superselekcji , oddzielone domeny niepowiązane skończonymi fluktuacjami.

Podwójność Kramersa-Wanniera

Kramers i Wannier byli w stanie wykazać, że ekspansja modelu w wysokiej temperaturze i ekspansja w niskiej temperaturze są równe całkowitemu przeskalowaniu energii swobodnej. Pozwoliło to na dokładne wyznaczenie punktu przejścia fazowego w modelu dwuwymiarowym (przy założeniu, że istnieje unikalny punkt krytyczny).

Zera Yang-Lee

Po rozwiązaniu Onsagera Yang i Lee zbadali, w jaki sposób funkcja podziału staje się osobliwa, gdy temperatura zbliża się do temperatury krytycznej.

Metody Monte Carlo do symulacji numerycznej

Definicje

Model Isinga może być często trudny do oceny numerycznej, jeśli w systemie jest wiele stanów. Rozważ model Ising z

L = |Λ|: całkowita liczba miejsc na siatce,

σ _j ∈ {−1, +1}: pojedyncze miejsce spinu na sieci, j  = 1, ..., L ,

S ∈ {−1, +1} ^L : stan systemu.

Ponieważ każda strona spinu ma ±1 spin, możliwe są 2 ^L różnych stanów. To uzasadnia symulację modelu Isinga przy użyciu metod Monte Carlo .

Hamiltona , który jest powszechnie stosowany do przedstawienia energii modelu przy użyciu metody Monte Carlo

${\ Displaystyle H (\ sigma) = - J \ suma _ {\ langle i ~ j \ rangle} \ sigma _ {i} \ sigma _ {j} -h \ suma _ {j} \ sigma _ {j}. }$

Co więcej, hamiltonian jest jeszcze bardziej uproszczony przez założenie zerowego pola zewnętrznego h , ponieważ na wiele pytań, które stawia się do rozwiązania za pomocą modelu, można odpowiedzieć przy braku pola zewnętrznego. To prowadzi nas do następującego równania energii dla stanu σ:

${\ Displaystyle H (\ sigma) = - J \ suma _ {\ langle i ~ j \ rangle} \ sigma _ {i} \ sigma _ {j}.}$

Mając ten hamiltonian, można obliczyć interesujące wielkości, takie jak ciepło właściwe lub namagnesowanie magnesu w danej temperaturze.

Algorytm Metropolis

Przegląd

Algorytm Metropolis-Hastings jest najczęściej stosowany algorytm Monte Carlo do obliczania model isinga szacunków. Algorytm najpierw wybiera prawdopodobieństwa wyboru g (μ, ν), które reprezentują prawdopodobieństwo, że stan ν zostanie wybrany przez algorytm spośród wszystkich stanów, przy założeniu, że jeden jest w stanie μ. Następnie używa prawdopodobieństw akceptacji A (μ, ν), aby zachować szczegółową równowagę . Jeżeli nowy stan ν zostanie zaakceptowany, to przechodzimy do tego stanu i powtarzamy z wyborem nowego stanu i podjęciem decyzji o jego akceptacji. Jeśli ν nie jest akceptowane, pozostajemy w μ. Proces ten jest powtarzany aż do spełnienia pewnego kryterium zatrzymania, co w modelu Isinga często ma miejsce, gdy sieć staje się ferromagnetyczna , co oznacza, że ​​wszystkie miejsca są skierowane w tym samym kierunku.

Realizując algorytm należy zadbać o to, aby g (μ, v) dobrać tak, aby zachowana była ergodyczność . W równowadze termicznej energia systemu waha się tylko w niewielkim zakresie. To jest motywacja koncepcji dynamiki pojedynczego spinu , która mówi, że w każdym przejściu zmienimy tylko jedno z miejsc spinu na siatce. Co więcej, stosując dynamikę pojedynczego spin-flip, można przejść z dowolnego stanu do dowolnego innego stanu, odwracając kolejno każdą stronę, która różni się między tymi dwoma stanami.

Maksymalna ilość zmiany między energią obecnego stanu, H _μ a jakąkolwiek możliwą energią nowego stanu H _ν (przy użyciu dynamiki pojedynczego spin-flip) wynosi 2 J między spinem, który zdecydujemy się „przerzucić”, aby przejść do nowego stanu i sąsiadem tego spinu. Zatem w jednowymiarowym modelu Isinga, w którym każde miejsce ma dwóch sąsiadów (lewego i prawego), maksymalna różnica energii wyniosłaby 4 J .

Niech c oznacza liczbę koordynacyjną sieci ; liczba najbliższych sąsiadów, których ma dowolna sieć kratownicowa. Zakładamy, że wszystkie lokalizacje mają taką samą liczbę sąsiadów ze względu na okresowe warunki brzegowe . Należy zauważyć, że algorytm Metropolis-Hastings nie działa dobrze wokół punktu krytycznego z powodu krytycznego spowolnienia. Do rozwiązania modelu w pobliżu punktu krytycznego wymagane są inne techniki, takie jak metody wielosiatkowe, algorytm Niedermayera, algorytm Swendsena-Wanga lub algorytm Wolffa; wymóg określenia krytycznych wykładników systemu.

Specyfikacja

Specjalnie dla modelu Isinga i wykorzystując dynamikę pojedynczego obrotu, można ustalić, co następuje.

Ponieważ na siatce znajduje się L wszystkich lokacji, przy użyciu pojedynczego obrotu jako jedynego sposobu przejścia do innego stanu, możemy zobaczyć, że jest w sumie L nowych stanów ν z naszego obecnego stanu μ. Algorytm zakłada, że ​​prawdopodobieństwa selekcji są równe stanom L : g (μ, ν) = 1/ L . Bilans szczegółowy mówi nam, że musi być spełnione następujące równanie:

${\displaystyle {\frac {P(\mu,\nu)}{P(\nu,\mu)}}={\frac {g(\mu,\nu)A(\mu,\nu)}{ g(\nu ,\mu )A(\nu ,\mu )}}={\frac {A(\mu ,\nu )}{A(\nu ,\mu )}}={\frac {P_{ \beta }(\nu )}{P_{\beta }(\mu )}}={\frac {{\frac {1}{Z}}e^{-\beta (H_{\nu })}} {{\frac {1}{Z}}e^{-\beta (H_{\mu })}}}=e^{-\beta (H_{\nu }-H_{\mu })}.}$

W związku z tym chcemy wybrać prawdopodobieństwo akceptacji, aby nasz algorytm spełniał wymagania

${\ Displaystyle {\ Frac {A (\ mu, \ nu)} {A (\ nu, \ mu)}} = e ^ {- \ beta (H_ {\ nu}-H_ {\ mu})}.}$

Jeśli H _ν > H _μ , to A (ν, μ) > A (μ, ν). Metropolis ustawia większą z A (μ, ν) lub A (ν, μ) na 1. W tym rozumowaniu algorytm akceptacji jest następujący:

${\ Displaystyle A (\ mu, \ nu) = {\ zacząć {przypadki} e ^ {- \ beta (H_ {\ nu} - H_ {\ mu})} i {\ tekst {jeśli}} H_ {\ nu }-H_{\mu }>0,\\1&{\text{inaczej}}.\end{przypadki}}}$

Podstawowa postać algorytmu jest następująca:

1. Wybierz miejsce spinu, korzystając z prawdopodobieństwa wyboru g (μ, v) i oblicz udział w energii tego spinu.
2. Odwróć wartość spinu i oblicz nowy wkład.
3. Jeśli nowa energia jest mniejsza, zachowaj odwróconą wartość.
4. Jeśli nowa energia jest większa, trzymaj się tylko z prawdopodobieństwem ${\ Displaystyle e ^ {-\ beta (H_ {\ nu} - H_ {\ mu})}.}$
5. Powtarzać.

Zmiana energii H _ν  −  H _μ zależy tylko od wartości spinu i jego najbliższych sąsiadów grafu. Więc jeśli wykres nie jest zbyt połączony, algorytm jest szybki. Ten proces ostatecznie wygeneruje wybór z dystrybucji.

Postrzeganie modelu Isinga jako łańcucha Markowa

Można postrzegać model Isinga jako łańcuch Markowa , ponieważ bezpośrednie prawdopodobieństwo przejścia P _β (ν) do przyszłego stanu ν zależy tylko od obecnego stanu μ. Algorytm Metropolis jest w rzeczywistości wersją symulacji Monte Carlo łańcucha Markowa , a ponieważ w algorytmie Metropolis stosujemy dynamikę pojedynczego obrotu, każdy stan może być postrzegany jako posiadający powiązania z dokładnie L innymi stanami, gdzie każde przejście odpowiada odwróceniu pojedyncza strona spinu do przeciwnej wartości. Ponadto, ponieważ zmiana równania energii H _σ zależy tylko od siły oddziaływania najbliższego sąsiada J , model Isinga i jego warianty, takie jak model Sznajda, można postrzegać jako formę modelu głosowania dla dynamiki opinii.

Jeden wymiar

Granica termodynamiczna istnieje tak długo, jak zanik oddziaływania ma wartość α > 1. ${\ Displaystyle J_ {ij} \ sim | ij | ^ {-\ alfa}}$

• W przypadku oddziaływania ferromagnetycznego z 1 < α < 2 Dyson udowodnił, porównując z przypadkiem hierarchicznym, że zachodzi przejście fazowe w wystarczająco małej temperaturze.${\ Displaystyle J_ {ij} \ sim | ij | ^ {-\ alfa}}$
• W przypadku oddziaływania ferromagnetycznego Fröhlich i Spencer udowodnili, że w wystarczająco małej temperaturze zachodzi przejście fazowe (w przeciwieństwie do przypadku hierarchicznego).${\ Displaystyle J_ {ij} \ sim | ij | ^ {-2}}$
• W przypadku oddziaływania o α > 2 (co obejmuje również oddziaływania skończenie zakresowe) nie ma przejścia fazowego w dowolnej temperaturze dodatniej (tj. skończonej β), ponieważ energia swobodna jest analityczna w parametrach termodynamicznych.${\ Displaystyle J_ {ij} \ sim | ij | ^ {-\ alfa}}$
• W przypadku oddziaływań najbliższych sąsiadów E. Ising podał dokładne rozwiązanie modelu. W dowolnej temperaturze dodatniej (tj. skończonej β) energia swobodna jest analityczna w parametrach termodynamiki, a obcięta dwupunktowa korelacja spinowa zanika wykładniczo szybko. W temperaturze zerowej (tj. nieskończonej β) zachodzi przejście fazowe drugiego rzędu: energia swobodna jest nieskończona, a obcięta dwupunktowa korelacja spinu nie zanika (pozostaje stała). Dlatego T = 0 jest temperaturą krytyczną tego przypadku. Formuły skalowania są spełnione.

Dokładne rozwiązanie Isinga

W przypadku najbliższego sąsiada (z okresowymi lub swobodnymi warunkami brzegowymi) dostępne jest dokładne rozwiązanie. Hamiltonian jednowymiarowego modelu Isinga na siatce miejsc L z okresowymi warunkami brzegowymi to

${\ Displaystyle H (\ sigma) = - J \ suma _ {i = 1, \ ldots, L-1} \ sigma _ {i} \ sigma _ {i + 1} -h \ suma _ {i} \ sigma _{i},}$

gdzie J i h mogą być dowolną liczbą, ponieważ w tym uproszczonym przypadku J jest stałą reprezentującą siłę oddziaływania między najbliższymi sąsiadami, a h jest stałym zewnętrznym polem magnetycznym przyłożonym do miejsc sieci. Wtedy wolna energia jest

${\ Displaystyle f (\ beta, h) = - \ lim _ {L \ do \ infty} {\ Frac {1} {\ beta L}} \ ln Z (\ beta) = - {\ Frac {1} { \beta }}\ln \left(e^{\beta J}\cosh \beta h+{\sqrt {e^{2\beta J}(\sinh \beta h)^{2}+e^{-2 \beta J}}}\prawo),}$

a korelacja spinowo-spinowa (tj. kowariancja) wynosi

${\ Displaystyle \ langle \ sigma _ {i} \ sigma _ {j} \ rangle - \ langle \ sigma _ {i} \ rangle \ langle \ sigma _ {j} \ rangle = C (\ beta) e ^ {- c(\beta )|ij|},}$

gdzie C (β) i c (β) są funkcjami dodatnimi dla T > 0. Jednak dla T → 0, długość korelacji odwrotnej c (β) znika.

Dowód

Dowodem tego wyniku jest proste obliczenie.

Jeśli h = 0, bardzo łatwo jest uzyskać energię swobodną w przypadku warunku brzegowego swobodnej, tj. gdy

${\ Displaystyle H (\ sigma ) = - J (\ sigma _ {1} \ sigma _ {2} + \ cdots + \ sigma _ {L-1} \ sigma _ {L}).}$

Następnie model ulega faktoryzacji pod wpływem zmiany zmiennych

${\ Displaystyle \ sigma '_ {j} = \ sigma _ {j} \ sigma _ {j-1} \ quad j \ geq 2.}$

To daje

${\ Displaystyle Z (\ beta ) = \ suma _ {\ sigma _ {1} \ ldots \ sigma _ {L}} e ^ {\ beta J \ sigma _ {1} \ sigma _ {2}} e ^{\beta J\sigma _{2}\sigma _{3}}\cdots e^{\beta J\sigma _{L-1}\sigma _{L}}=2\prod _{j=2 }^{L}\sum _{\sigma '_{j}}e^{\beta J\sigma '_{j}}=2\left[e^{\beta J}+e^{-\beta J}\right]^{L-1}.}$

Dlatego darmowa energia jest

${\ Displaystyle f (\ beta , 0) = - {\ Frac {1} {\ beta}} \ ln \ lewo [e ^ {\ beta J} + e ^ {-\ beta J} \ prawej].}$

Z tą samą zmianą zmiennych

${\ Displaystyle \ langle \ sigma _ {j} \ sigma _ {j + N} \ rangle = \ lewo [{\ Frac {e ^ {\ beta J}-e ^ {-\ beta J}} {e ^ { \beta J}+e^{-\beta J}}}\right]^{N},}$

stąd rozpada się wykładniczo, gdy T ≠ 0; ale dla T = 0, czyli w granicy β → ∞ nie ma rozpadu.

Jeśli h ≠ 0 potrzebujemy metody macierzy przejścia. Dla okresowych warunków brzegowych przypadek jest następujący. Funkcja partycji to

${\ Displaystyle Z (\ beta ) = \ suma _ {\ sigma _ {1} \ ldots \ sigma _ {L}} e ^ {\ beta h \ sigma _ {1}} e ^ {\ beta J \ sigma _{1}\sigma _{2}}e^{\beta h\sigma _{2}}e^{\beta J\sigma _{2}\sigma _{3}}\cdots e^{\ beta h\sigma _{L}}e^{\beta J\sigma _{L}\sigma _{1}}=\sum _{\sigma _{1},\ldots ,\sigma _{L}} V_{\sigma _{1},\sigma _{2}}V_{\sigma _{2},\sigma _{3}}\cdots V_{\sigma _{L},\sigma _{1}} .}$

Współczynniki mogą być postrzegane jako wpisy macierzy. Do wyboru są różne opcje: wygodny (bo matryca jest symetryczna) to ${\displaystyle V_{\sigma,\sigma '}}$

${\ Displaystyle V_ {\ sigma, \ sigma '} = e ^ {{\ Frac {\ beta h} {2}} \ sigma} e ^ {\ beta J \ sigma \ sigma '} e ^ {{\ Frac { \beta h}{2}}\sigma '}}$

lub

${\ Displaystyle V = {\ zacząć {bmatrix} e ^ {\ beta (h + J)} i e ^ {- \ beta J} \ \ e ^ {- \ beta J} i e ^ {- \ beta (hJ)} \end{bmatryca}}.}$

W formalizmie macierzowym

${\ Displaystyle Z (\ beta) = \ operatorname {Tr} \ lewo (V ^ {L} \ prawej) = \ lambda _ {1} ^ { l} + \ lambda _ {2} ^ { l} = \ lambda _{1}^{L}\left[1+\left({\frac {\lambda _{2}}{\lambda _{1}}}\right)^{L}\right],}$

gdzie λ ₁ jest najwyższą wartością własną V , a λ ₂ jest drugą wartością własną:

${\ Displaystyle \ lambda _ {1} = e ^ {\ beta J} \ cosh \ beta h + {\ sqrt {e ^ {2 \ beta J} (\ sinh \ beta h) ^ {2} + e ^ {- 2\beta J}}},}$

oraz |λ ₂ | < λ ₁ . Daje to formułę energii swobodnej.

Uwagi

Energia najniższego stanu to − JL , gdy wszystkie spiny są takie same. Dla każdej innej konfiguracji dodatkowa energia jest równa 2 J razy liczba zmian znaku, które występują podczas skanowania konfiguracji od lewej do prawej.

Jeżeli liczbę zmian znaku w konfiguracji oznaczymy jako k , to różnica energii od stanu o najniższej energii wynosi 2 k . Ponieważ energia sumuje się do liczby przewrotów, prawdopodobieństwo p wystąpienia przewrotu w każdej pozycji jest niezależne. Stosunek prawdopodobieństwa znalezienia klapki do prawdopodobieństwa jej nie znalezienia to czynnik Boltzmanna:

${\ Displaystyle {\ Frac {p} {1-p}} = e ^ {-2 \ beta J}.}$

Problem sprowadza się do niezależnych, tendencyjnych rzutów monetą . To zasadniczo uzupełnia opis matematyczny.

Z opisu w kategoriach niezależnych rzutów można zrozumieć statystyki modelu dla długich linii. Linia dzieli się na domeny. Każda domena ma średnią długość exp(2β). Długość domeny rozkłada się wykładniczo, ponieważ na każdym etapie istnieje stałe prawdopodobieństwo napotkania przewrotu. Domeny nigdy nie stają się nieskończone, więc długi system nigdy nie jest namagnesowany. Każdy krok zmniejsza korelację między spinem a jego sąsiadem o wielkość proporcjonalną do p , więc korelacje spadają wykładniczo.

${\ Displaystyle \ langle S_ {i} S_ {j} \ rangle \ propto e ^ {-p | ij |}}.$

Funkcja podziału to objętość konfiguracji, przy czym każda konfiguracja jest ważona wagą Boltzmanna. Ponieważ każda konfiguracja jest opisana przez zmiany znaku, funkcja partycji rozkłada na czynniki:

${\ Displaystyle Z = \ suma _ {\ tekst {konfiguracje}} e ^ {\ suma _ {k} S_ {k}} = \ prod _ {k} (1 + p) = (1 + p) ^ {L }.}$

Logarytm podzielony przez L to gęstość energii swobodnej:

${\ Displaystyle \ beta f = \ log (1 + p) = \ log \ lewo (1 + {\ Frac {e ^ {-2 \ beta J}} {1 + e ^ {-2 \ beta J}}} \Prawidłowy),}$

co jest analityczne z dala od β = ∞. Znakiem przejścia fazowego jest nieanalityczna energia swobodna, więc model jednowymiarowy nie ma przejścia fazowego.

Rozwiązanie jednowymiarowe z polem poprzecznym

Aby wyrazić hamiltonian Isinga za pomocą kwantowo-mechanicznego opisu spinów, zastępujemy zmienne spinów ich odpowiednimi macierzami Pauliego. Jednak w zależności od kierunku pola magnetycznego możemy stworzyć hamiltonian pola poprzecznego lub pola podłużnego. Poprzecznego pola Hamiltona jest przez

${\ Displaystyle H (\ sigma) = - J \ suma _ {i = 1, \ ldots, L} \ sigma _ {i} ^ {z} \ sigma _ {i + 1} ^ {z} - h \ suma _{i}\sigma _{i}^{x}.}$

Model pola poprzecznego doświadcza przejścia fazowego między reżimem uporządkowanym i nieuporządkowanym w J  ~  h . Można to pokazać za pomocą mapowania macierzy Pauliego

${\ Displaystyle \ sigma _ {n} ^ {z} = \ prod _ {i = 1} ^ {n} T_ {i} ^ {x}}$

${\ Displaystyle \ sigma _ {n} ^ {x} = T_ {n} ^ {z} T_ {n + 1} ^ {z}.}$

Po przepisaniu hamiltonianu pod kątem tej macierzy zmiany bazy otrzymujemy:

${\ Displaystyle H (\ sigma) = - h \ suma _ {i = 1, \ ldots, L} T_ {i} ^ {z} T_ {i + 1} ^ {z} - J \ suma _ {i} T_{i}^{x}.}$

Ponieważ role h i J są zamienione, hamiltonian przechodzi przejście w J = h .

Dwa wymiary

• W przypadku ferromagnetycznym występuje przejście fazowe. W niskiej temperaturze argument Peierlsa dowodzi dodatniego namagnesowania dla przypadku najbliższego sąsiada, a następnie, przez nierówność Griffitha , również przy dodawaniu oddziaływań o dłuższym zasięgu. Tymczasem w wysokiej temperaturze rozszerzenie klastra daje analityczność funkcji termodynamicznych.
• W przypadku najbliższego sąsiedztwa energia swobodna została dokładnie obliczona przez Onsagera poprzez równoważność modelu ze swobodnymi fermionami na sieci. Funkcje korelacji spinowo-spinowej obliczyli McCoy i Wu.

Dokładne rozwiązanie Onsagera

Onsager (1944) uzyskał następujące wyrażenie analityczne na energię swobodną modelu Isinga na anizotropowej sieci kwadratowej, gdy pole magnetyczne w granicy termodynamicznej w funkcji temperatury oraz energii oddziaływań poziomych i pionowych i odpowiednio ${\ Displaystyle h = 0}$${\displaystyle J_{1}}$${\displaystyle J_{2}}$

${\ Displaystyle - \ beta f = \ ln 2+ {\ Frac {1} {8 \ pi ^ {2}}} \ int _ {0} ^ {2 \ pi} d \ theta _ {1} \ int _ {0}^{2\pi }d\theta _{2}\ln[\cosh(2\beta J_{1})\cosh(2\beta J_{2})-\sinh(2\beta J_{ 1})\cos(\theta _{1})-\sinh(2\beta J_{2})\cos(\theta _{2})].}$

Z tego wyrażenia na energię swobodną można obliczyć wszystkie funkcje termodynamiczne modelu, stosując odpowiednią pochodną. Model 2D Isinga był pierwszym modelem, który wykazywał ciągłe przejście fazowe w dodatniej temperaturze. Występuje w temperaturze, która rozwiązuje równanie ${\displaystyle T_{c}}$

${\ Displaystyle \ sinh \ lewo ({\ Frac {2J_ {1}} {kT_ {c}}} \ prawej) \ sinh \ lewo ({\ Frac {2J_ {2}} {kT_ {c}}} \ po prawej )=1.}$

W przypadku izotropowym, gdy energie oddziaływań poziomych i pionowych są równe , temperatura krytyczna występuje w następnym punkcie ${\displaystyle J_{1}=J_{2}=J}$${\displaystyle T_{c}}$

${\ Displaystyle T_ {c} = {\ Frac {2J} {k \ ln (1+ {\ sqrt {2}})}}}$

Gdy energia interakcji , to zarówno ujemne, model Isinga staje się antiferromagnet. Ponieważ sieć kwadratowa jest dwudzielna, jest niezmienna w przypadku tej zmiany pola magnetycznego , więc energia swobodna i temperatura krytyczna są takie same dla przypadku antyferromagnetycznego. W przypadku sieci trójkątnej, która nie jest dwudzielna, ferromagnetyczny i antyferromagnetyczny model Isinga zachowują się wyraźnie odmiennie. ${\displaystyle J_{1}}$${\displaystyle J_{2}}$${\ Displaystyle h = 0}$

Matryca transferowa

Zacznij od analogii z mechaniką kwantową. Model Isinga na długiej sieci okresowej ma funkcję podziału

${\ Displaystyle \ suma _ {\ {S \}} \ exp {\ biggl (} \ suma _ {ij} S_ {i, j} \ lewo (S_ {i, j + 1} + S_ {i + 1, j}\prawo){\biggr )}.}$

Pomyśl o kierunku i jako przestrzeni , a kierunku j jako o czasie . Jest to niezależna suma wszystkich wartości, które spiny mogą przyjąć w każdym wycinku czasu. Jest to rodzaj całki po ścieżce , jest to suma wszystkich historii spinów.

Całkę po ścieżce można przepisać jako ewolucję Hamiltona. Hamiltonian przechodzi przez czas wykonując rotację jednostkową pomiędzy czasem t a czasem t + Δ t :

${\ Displaystyle U = e ^ {iH \ Delta t}}$

Iloczyn macierzy U, jednej po drugiej, jest całkowitym operatorem ewolucji w czasie, który jest całką po ścieżce, od której zaczęliśmy.

${\ Displaystyle U ^ {N} = (e ^ {iH \ Delta t}) ^ {N} = \ int DXe ^ {iL}}$

gdzie N to liczba przedziałów czasu. Suma na wszystkich ścieżkach jest iloczynem macierzy, każdy element macierzy jest prawdopodobieństwem przejścia z jednego wycinka do drugiego.

Podobnie można podzielić sumę na wszystkie konfiguracje funkcji podziału na wycinki, gdzie każdy wycinek jest jednowymiarową konfiguracją w czasie 1. Określa to macierz transferu :

${\displaystyle T_{C_{1}C_{2}}.}$

Konfiguracja w każdym plastrze jest jednowymiarowym zbiorem obrotów. W każdym przedziale czasu T zawiera elementy macierzy pomiędzy dwiema konfiguracjami spinów, jedną w najbliższej przyszłości i jedną w najbliższej przeszłości. Te dwie konfiguracje C ₁ i C ₂ oraz są wszystkie kombinacje jednowymiarowej wirowania. Możemy myśleć o przestrzeni wektorowej, na którą działa T , jako o wszystkich ich złożonych kombinacjach liniowych. Korzystanie z notacji mechaniki kwantowej:

${\ Displaystyle | A \ rangle = \ suma _ {S} A (S) | S \ rangle}$

gdzie każdy wektor bazowy jest konfiguracją spinową jednowymiarowego modelu Isinga. ${\displaystyle |S\rangle}$

Podobnie jak hamiltonian, macierz przejścia działa na wszystkie liniowe kombinacje stanów. Funkcja podziału jest funkcją macierzową T, która jest zdefiniowana przez sumę po wszystkich historiach, które powracają do pierwotnej konfiguracji po N krokach:

${\ Displaystyle Z = \ operatorname {tr} (T ^ {N}).}$

Ponieważ jest to równanie macierzowe, można je oszacować na dowolnej podstawie. Więc jeśli możemy diagonalizować macierz T , możemy znaleźć Z .

T pod względem matryc Pauliego

Udział w funkcji podziału dla każdej przeszłej/przyszłej pary konfiguracji w wycinku jest sumą dwóch składników. Istnieje liczba przewrotów obrotowych w poprzednim wycinku oraz liczba przewrotów obrotowych między przeszłym i przyszłym wycinek. Zdefiniuj operator w konfiguracjach, które odwracają obrót w miejscu i:

${\ Displaystyle \ sigma _ {i} ^ {x}.}$

W zwykłej bazie Isinga, działając na dowolną kombinację liniową przeszłych konfiguracji, wytwarza tę samą kombinację liniową, ale z odwróconym obrotem w pozycji i każdego wektora bazowego.

Zdefiniuj drugi operator, który mnoży wektor bazowy przez +1 i -1 zgodnie z obrotem w pozycji i :

${\ Displaystyle \ sigma _ {i} ^ {z}.}$

T można zapisać w następujący sposób:

${\ Displaystyle \ suma _ {i} A \ sigma _ {i} ^ {x} + B \ sigma _ {i} ^ {z} \ sigma _ {i + 1} ^ {z}}$

gdzie A i B są stałymi, które należy określić, aby odtworzyć funkcję podziału. Interpretacja polega na tym, że konfiguracja statystyczna w tym wycinku wpływa zarówno na liczbę przewrotów rotacji w wycinku, jak i na to, czy obrót w pozycji i został przewrócony.

Operatory tworzenia i anihilacji spin flip

Podobnie jak w przypadku jednowymiarowym, przeniesiemy uwagę ze spinów na spin-flipy. Wyraz σ ^z w T zlicza liczbę przewrotów spinowych, które możemy zapisać w postaci operatorów tworzenia i anihilacji spin-flip:

${\ Displaystyle \ suma C \ psi _ {i} ^ {\ sztylet} \ psi _ {i}. \,}$

Pierwszy termin odwraca spin, więc w zależności od podstawy określ albo:

1. przesuwa spin-flip o jedną jednostkę w prawo
2. przesuwa spin-flip o jedną jednostkę w lewo
3. wykonuje dwa spin-flipy na sąsiednich stronach
4. niszczy dwa spin-flipy na sąsiednich stronach.

Zapisując to w kategoriach operatorów kreacji i anihilacji:

${\ Displaystyle \ sigma _ {i} ^ {x} = D {\ psi ^ {\ sztylet}} _ {i} \ psi _ {i + 1} + D ^ {*} {\ psi ^ {\ sztylet} }_{i}\psi _{i-1}+C\psi _{i}\psi _{i+1}+C^{*}{\psi ^{\dagger }}_{i}{\ psi ^{\sztylet }}_{i+1}.}$

Zignoruj ​​stałe współczynniki i skup uwagę na formularzu. Wszystkie są kwadratowe. Ponieważ współczynniki są stałe, oznacza to, że macierz T może być diagonalizowana przez transformaty Fouriera.

Przeprowadzenie diagonalizacji wytwarza darmową energię Onsagera.

Wzór Onsagera na spontaniczne namagnesowanie

Onsager ogłosił na dwóch różnych konferencjach w 1948 r. następujące wyrażenie na spontaniczne namagnesowanie M dwuwymiarowego ferromagnesu Isinga na siatce kwadratowej, choć bez dowodu

${\ Displaystyle M = \ lewo (1-\ lewo [\ sinh 2 \ beta J_ {1} \ sinh 2 \ beta J_ {2} \ prawej] ^ {-2} \ po prawej) ^ {\ Frac {1} { 8}}}$

gdzie i są poziomymi i pionowymi energiami interakcji. ${\displaystyle J_{1}}$${\displaystyle J_{2}}$

Kompletne wyprowadzenie zostało podane dopiero w 1951 r. przez Yanga (1952) przy użyciu procesu limitującego macierzy przenoszenia wartości własnych. Dowód następnie znacznie uproszczone w 1963 roku przez Montroll Potts i Ward pomocą Szegő jest wzór graniczną dla determinant Toeplitza traktując namagnesowanie jako ograniczenie funkcji korelacji.

Minimalny model

W punkcie krytycznym dwuwymiarowy model Isinga jest dwuwymiarową konforemną teorią pola . Funkcje korelacji spinu i energii są opisane przez model minimalny , który został dokładnie rozwiązany.

Trzy wymiary

W trzech, podobnie jak w dwóch wymiarach, najlepiej zbadanym przypadkiem modelu Isinga jest model niezmienniczy translacji na sieci sześciennej ze sprzężeniem najbliższych sąsiadów w zerowym polu magnetycznym. Czołowi teoretycy przez wiele dziesięcioleci poszukiwali analitycznego rozwiązania trójwymiarowego, które byłoby analogiczne do rozwiązania Onsagera w przypadku dwuwymiarowym. Obecnie uważa się, że takie rozwiązanie nie istnieje, chociaż nie ma na to dowodów.

W trzech wymiarach Aleksander Poliakow i Władimir Dotsenko pokazali, że model Isinga przedstawiany jest w kategoriach nieoddziałujących ze sobą strun fermionowych . Konstrukcję tę przeprowadzono na siatce, a granica kontinuum, przypuszczalnie opisująca punkt krytyczny, jest nieznana.

Wynik NP-zupełności Istraila dla ogólnego modelu szkła spinowego

W 2000 r. Sorin Istrail z Sandia National Laboratories udowodnił, że nieplanarny model Isinga jest NP-zupełny . Oznacza to, że zakładając P ≠ NP, ogólny model Isinga ze szkła spinowego jest dokładnie rozwiązywalny tylko w przypadkach planarnych , więc rozwiązania dla wymiarów wyższych niż dwa są również niewykonalne. Wynik Istraila dotyczy tylko modelu szkła spinowego z przestrzennie zmiennymi sprzężeniami i nie mówi nic o oryginalnym modelu ferromagnetycznym Isinga z równymi sprzężeniami.

Przejście fazowe

W trzech, jak w dwóch wymiarach, argument Peierla pokazuje, że zachodzi przejście fazowe. To przejście fazowe jest ściśle znane jako ciągłe (w tym sensie, że długość korelacji jest rozbieżna, a namagnesowanie dochodzi do zera) i jest nazywane punktem krytycznym . Uważa się, że punkt krytyczny można opisać jako stały punkt przekształcenia grupy renormalizacji Wilsona-Kadanoffa. Uważa się również, że przejście fazowe można opisać za pomocą trójwymiarowej jednolitej teorii pola konforemnego, o czym świadczą symulacje Monte Carlo i argumenty teoretyczne. Chociaż rygorystyczne ustalenie obrazu grupy renormalizacji lub obrazu konforemnej teorii pola jest otwartym problemem, fizycy teoretyczni wykorzystali te dwie metody do obliczenia krytycznych wykładników przejścia fazowego, które są zgodne z eksperymentami i symulacjami Monte Carlo.

Ta konforemna teoria pola opisująca trójwymiarowy punkt krytyczny Isinga jest aktywnie badana przy użyciu metody konforemnego ładowania początkowego . Metoda ta dostarcza obecnie najdokładniejszych informacji o strukturze teorii krytycznej (patrz Ising Critical exponents ).

Cztery wymiary i więcej

W dowolnym wymiarze model Isinga można produktywnie opisać za pomocą lokalnie zmieniającego się pola średniej. Pole jest definiowane jako średnia wartość spinu w dużym regionie, ale nie tak duża, aby obejmowała cały system. Pole nadal ma powolne zmiany z punktu do punktu, ponieważ uśredniona objętość się porusza. Te fluktuacje pola są opisane przez ciągłą teorię pola w granicy systemu nieskończonego.

Pole lokalne

Pole H jest zdefiniowane jako składowe Fouriera o długich falach zmiennej spinowej, w granicach, w których długości fal są długie. Istnieje wiele sposobów obliczania średniej długości fali, w zależności od szczegółów dotyczących odcinania długich fal. Szczegóły nie są zbyt ważne, ponieważ celem jest znalezienie statystyk H, a nie spinów. Gdy znane są korelacje w H , długodystansowe korelacje między spinami będą proporcjonalne do długodystansowych korelacji w H .

Dla dowolnej wartości wolno zmieniającego się pola H energia swobodna (log-prawdopodobieństwo) jest lokalną funkcją analityczną H i jego gradientów. Energia swobodna F ( H ) jest zdefiniowana jako suma wszystkich konfiguracji Isinga, które są zgodne z polem o długich falach. Ponieważ H jest opisem zgrubnym, istnieje wiele konfiguracji Ising zgodnych z każdą wartością H , o ile dopasowanie nie wymaga zbyt dużej dokładności.

Ponieważ dozwolony zakres wartości spinu w dowolnym regionie zależy tylko od wartości H w obrębie jednej średniej objętości z tego regionu, udział energii swobodnej z każdego regionu zależy tylko od wartości H tam i w sąsiednich regionach. Zatem F jest sumą po wszystkich regionach wkładu lokalnego, który zależy tylko od H i jego pochodnych.

Przez symetrię w H , tylko parzyste potęgi mają udział. Dzięki symetrii odbicia na siatce kwadratowej mają udział tylko parzyste potęgi gradientów. Zapisanie kilku pierwszych pojęć w energii darmowej:

${\ Displaystyle \ beta F = \ int d ^ {d} x \ lewo [AH ^ {2} + \ suma _ {i = 1} ^ {d} Z_ {i} (\ częściowy _ {i} H) ^ {2}+\lambda H^{4}+\cdots \right].}$

Na siatce kwadratowej symetrie gwarantują, że wszystkie współczynniki Z _i członów pochodnych są równe. Ale nawet na model isinga anizotropowego, gdzie Z _I ' s w różnych kierunkach są różne, wahania H są izotropowe w układzie współrzędnych, gdzie różne kierunki przestrzeni są przeskalowanym.

Na dowolnej sieci wyraz pochodny

${\ Displaystyle Z_ {ij} \, \ częściowy _ {i} H \, \ częściowy _ {j} H}$

jest dodatnią określoną formą kwadratową i może służyć do definiowania metryki przestrzeni. Zatem każdy translacyjny niezmienniczy model Isinga jest niezmienniczy rotacyjnie na długich dystansach, we współrzędnych, które sprawiają, że Z _ij = δ _ij . Symetria obrotowa pojawia się spontanicznie na dużych odległościach tylko dlatego, że nie ma zbyt wielu wyrazów niskiego rzędu. W punktach wielokrytycznych wyższego rzędu ta przypadkowa symetria jest tracona.

Ponieważ β F jest funkcją wolno zmieniającego się przestrzennie pola, prawdopodobieństwo dowolnej konfiguracji pola wynosi:

${\ Displaystyle P (H) \ propto e ^ {- \ int d ^ {d} x \ lewo [AH ^ {2} + Z | \ nabla H | ^ {2} + \ lambda H ^ {4} \ prawej ]}.}$

Średnia statystyczna dowolnego produktu terminów H jest równa:

${\ Displaystyle \ langle H (x_ {1}) H (x_ {2}) \ cdots H (x_ {n}) \ rangle = {\ int DH \, P (H) H (x_ {1}) H ( x_{2})\cdots H(x_{n}) \over \int DH\,P(H)}.}$

Mianownik w tym wyrażeniu nazywa się funkcją podziału , a całka po wszystkich możliwych wartościach H jest całką po ścieżce statystycznej. Całkuje on exp(β F ) po wszystkich wartościach H , po wszystkich składowych Fouriera spinów o długich falach. F jest euklidesowym lagranżjanem dla pola H , jedyną różnicą między tą a kwantową teorią pola pola skalarnego jest to, że wszystkie człony pochodne wchodzą ze znakiem dodatnim i nie ma ogólnego współczynnika i .

${\ Displaystyle Z = \ int DH \ e ^ {- \ int d ^ {d} x \ lewo [AH ^ {2} + Z | \ nabla H | ^ {2} + \ lambda H ^ {4} \ Prawidłowy]}}$

Analiza wymiarowa

Postać F może służyć do przewidywania, które terminy są najważniejsze w analizie wymiarowej. Analiza wymiarowa nie jest całkowicie prosta, ponieważ skalowanie H musi zostać określone.

W przypadku ogólnym wybór prawa skalowania dla H jest łatwy, ponieważ jedynym wyrazem, który się przyczynia, jest pierwszy,

${\ Displaystyle F = \ int d ^ {d} x \ AH ^ {2}.}$

Ten termin jest najbardziej znaczący, ale daje banalne zachowanie. Ta forma energii swobodnej jest ultralokalna, co oznacza, że ​​jest sumą niezależnego wkładu z każdego punktu. Przypomina to przewroty w jednowymiarowym modelu Isinga. Każda wartość H w dowolnym punkcie zmienia się całkowicie niezależnie od wartości w dowolnym innym punkcie.

Skalę pola można przedefiniować, aby zaabsorbować współczynnik A , i wtedy jasne jest, że A określa tylko ogólną skalę wahań. Model ultralokalny opisuje zachowanie modelu Isinga w wysokiej temperaturze na długich falach, ponieważ w tym limicie średnie fluktuacji są niezależne od punktu do punktu.

Aby znaleźć punkt krytyczny, obniż temperaturę. Wraz ze spadkiem temperatury wahania H rosną, ponieważ wahania są bardziej skorelowane. Oznacza to, że średnia z dużej liczby spinów nie staje się tak szybko mała, jak gdyby były nieskorelowane, ponieważ zwykle są takie same. Odpowiada to zmniejszeniu A w układzie jednostek, w którym H nie pochłania A . Przejście fazowe może nastąpić tylko wtedy, gdy składowe podrzędne w F mogą się przyczynić, ale ponieważ pierwszy człon dominuje na dużych odległościach, współczynnik A musi być dostrojony do zera. To jest lokalizacja punktu krytycznego:

${\ Displaystyle F = \ int d ^ {d} x \ lewo [tH ^ {2} + \ lambda H ^ {4} + Z (\ nabla H) ^ {2} \ prawej]}$

gdzie t jest parametrem, który przechodzi przez zero na przejściu.

Ponieważ t znika, ustalenie skali pola za pomocą tego terminu powoduje, że inne terminy wybuchają. Gdy t jest małe, skala pola może być ustawiona na ustalenie współczynnika składnika H ⁴ lub składnika (∇ H ) ² na 1.

Namagnesowanie

Aby znaleźć namagnesowanie, ustal skalowanie H tak, aby λ było jedynką. Teraz pole H ma wymiar − d /4, więc H ⁴ d ^d x jest bezwymiarowe, a Z ma wymiar 2 −  d /2. W tym skalowaniu składnik gradientu jest ważny tylko przy dużych odległościach dla d ≤ 4. Powyżej czterech wymiarów, przy długich długościach fal, na ogólne namagnesowanie wpływają tylko składniki ultralokalne.

Jest jeden subtelny punkt. Pole H zmienia się statystycznie, a fluktuacje mogą przesunąć punkt zerowy t . Aby zobaczyć jak, rozważ podział H ⁴ w następujący sposób:

${\ Displaystyle H (x) ^ {4} = - \ langle H (x) ^ {2} \ rangle ^ {2} + 2 \ langle H (x) ^ {2} \ rangle H (x) ^ {2} }+\left(H(x)^{2}-\langle H(x)^{2}\rangle \right)^{2}}$

Pierwszy człon jest stałym wkładem do darmowej energii i można go zignorować. Drugi wyraz to skończone przesunięcie w t . Trzeci składnik to wielkość, która skaluje się do zera na dużych odległościach. Oznacza to, że podczas analizowania skalowania t za pomocą analizy wymiarowej ważne jest przesunięcie t . Było to historycznie bardzo mylące, ponieważ przesunięcie w t przy dowolnym skończonym λ jest skończone, ale w pobliżu przejścia t jest bardzo małe. Ułamkowa zmiana w t jest bardzo duża, aw jednostkach, w których t jest ustalone, przesunięcie wygląda na nieskończone.

Namagnesowanie jest na poziomie minimum energii swobodnej i jest to równanie analityczne. Pod względem przesuniętego t ,

${\ Displaystyle {\ częściowy \ nad \ częściowy H} \ lewo (tH ^ {2} + \ lambda H ^ {4} \ po prawej) = 2 tH + 4 \ lambda H ^ {3} = 0}$

Dla t < 0 minima są w H proporcjonalne do pierwiastka kwadratowego z t . Tak więc argument katastrofy Landaua jest poprawny w wymiarach większych niż 5. Wykładnik namagnesowania w wymiarach większych niż 5 jest równy wartości średniego pola.

Gdy t jest ujemne, fluktuacje wokół nowego minimum są opisane przez nowy dodatni współczynnik kwadratowy. Ponieważ termin ten zawsze dominuje, w temperaturach poniżej przejścia fluktuacje ponownie stają się ultralokalne na dużych odległościach.

Wahania

Aby znaleźć zachowanie fluktuacji, przeskaluj pole, aby naprawić składnik gradientu. Wtedy wymiar skalowania długości pola wynosi 1 −  d /2. Teraz pole ma stałe kwadratowe fluktuacje przestrzenne we wszystkich temperaturach. Wymiar skali członu H ² wynosi 2, natomiast wymiar skali członu H ⁴ wynosi 4 −  d . Dla d < 4 składnik H ⁴ ma dodatni wymiar skali. W wymiarach większych niż 4 ma ujemne wymiary skali.

To zasadnicza różnica. Wymiary większe niż 4, mocujące skalę pomocą gradientu że określony współczynnik H ⁴ terminu jest mniej ważny w coraz dłuższych fal. Wymiar, w którym wkłady niekwadratowe zaczynają się przyczyniać, jest znany jako wymiar krytyczny. W modelu Isinga wymiarem krytycznym jest 4.

W wymiarach powyżej 4 krytyczne fluktuacje są opisywane przez czysto kwadratową energię swobodną przy długich długościach fal. Oznacza to, że wszystkie funkcje korelacji można obliczyć na podstawie średnich gaussowskich :

${\ Displaystyle \ langle S (x) S (y) \ rangle \ propto \ langle H (x) H (y) \ rangle = G (xy) = \ int {dk \ ponad (2 \ pi) ^ {d} }{e^{ik(xy)} \over k^{2}+t}}$

ważne, gdy x  −  y jest duże. Funkcja G ( x  −  y ) jest analityczną kontynuacją czasu urojonego propagatora Feynmana , ponieważ energia swobodna jest analityczną kontynuacją działania pola kwantowego dla swobodnego pola skalarnego. Dla wymiarów 5 i wyższych wszystkie inne funkcje korelacji na dużych odległościach są następnie określane przez twierdzenie Wicka . Wszystkie nieparzyste momenty wynoszą zero, przy symetrii ±. Momenty parzyste są sumą po całym podziale na pary iloczynu G ( x  −  y ) dla każdej pary.

${\ Displaystyle \ langle S (x_ {1}) S (x_ {2}) \ cdots S (x_ {2n}) \ rangle = C ^ {n} \ suma G (x_ {i1}, x_ {j1}) G(x_{i2},x_{j2})\ldots G(x_{in},x_{jn})}$

gdzie C jest stałą proporcjonalności. Więc znajomość G wystarczy. Określa wszystkie wielopunktowe korelacje pola.

Krytyczna funkcja dwupunktowa

Aby określić postać G , weź pod uwagę, że pola w całce po trajektorii są zgodne z klasycznymi równaniami ruchu wyprowadzonymi przez zmianę energii swobodnej:

${\ Displaystyle {\ zacząć {wyrównany} i \ lewo (- \ nabla _ {x} ^ {2} + t \ po prawej) \ langle H (x) H (y) \ rangle & = 0 \ \ \ rightarrow {} &&\nabla ^{2}G(x)+tG(x)&=0\end{wyrównany}}}$

Jest to ważne tylko w nieprzypadkowych punktach, ponieważ korelacje H są osobliwe, gdy punkty się zderzają. H przestrzega klasycznych równań ruchu z tego samego powodu, dla którego stosują się do nich operatorzy mechaniki kwantowej — jego fluktuacje są określone przez całkę po trajektorii.

W punkcie krytycznym t = 0 jest to równanie Laplace'a , które można rozwiązać metodą Gaussa z elektrostatyki. Zdefiniuj analogowe pole elektryczne przez

${\ Displaystyle E = \ nabla G}$

Z dala od źródła:

${\ Displaystyle \ nabla \ cdot E = 0}$

ponieważ G jest sferycznie symetryczne w wymiarach d , a E jest promieniowym gradientem G . Całkowanie na dużej  sferze d − 1 wymiarowej,

${\ Displaystyle \ int d ^ {d-1} SE_ {r} = \ operatorname {stała}}$

To daje:

${\ Displaystyle E = {C \ nad r ^ {d-1}}}$

a G można znaleźć całkując względem r .

${\ Displaystyle G (r) = {C \ nad r ^ {d-2}}}$

Stała C ustala ogólną normalizację pola.

G ( r ) z dala od punktu krytycznego

Gdy t nie jest równe zeru, tak że H waha się w temperaturze nieco odbiegającej od krytycznej, funkcja dwóch punktów zanika na dużych odległościach. Równanie, którego przestrzega, zostaje zmienione:

${\ Displaystyle \ nabla ^ {2} G + tG = 0 \ do {1 \ nad r ^ {d-1}} {d \ nad dr} \ lewo (r ^ {d-1} {dG \ nad dr} \right)+tG(r)=0}$

Dla r small w porównaniu z , rozwiązanie różni się dokładnie tak samo, jak w przypadku krytycznym, ale zachowanie na długich dystansach jest modyfikowane. ${\displaystyle {\sqrt {t}}}$

Aby zobaczyć jak, wygodnie jest przedstawić funkcję dwóch punktów jako całkę, wprowadzoną przez Schwingera w kontekście kwantowej teorii pola:

${\ Displaystyle G (x) = \ int d \ tau {1 \ nad \ lewo ({\ sqrt {2 \ pi \ tau}} \ po prawej) ^ {d}} e ^ {- {x ^ {2} \ ponad 4\tau }-t\tau }}$

To jest G , ponieważ transformacja Fouriera tej całki jest łatwa. Każdy ustalony wkład τ jest gaussowskim w x , którego transformata Fouriera jest innym gaussowskim o odwrotności szerokości w k .

${\ Displaystyle G (k) = \ int d \ tau e ^ {- (k ^ {2}-t) \ tau} = {1 \ ponad k ^ {2}-t}}$

Jest to odwrotność operatora ∇ ²  −  t w przestrzeni k , działającego na funkcję jednostkową w przestrzeni k , która jest transformatą Fouriera źródła funkcji delta zlokalizowanego w punkcie początkowym. Tak więc spełnia to samo równanie co G z tymi samymi warunkami brzegowymi, które określają siłę rozbieżności przy 0.

Interpretacja reprezentacji całkowej w odpowiednim czasie τ polega na tym, że funkcja dwupunktowa jest sumą wszystkich ścieżek błądzenia losowego, które łączą pozycję 0 z pozycją x w czasie τ. Gęstość tych ścieżek w czasie τ w pozycji x jest gaussowska, ale losowe spacerowicze znikają w stałym tempie proporcjonalnym do t, tak że gaussowski w czasie τ zmniejsza się o współczynnik, który stale maleje wykładniczo. W kontekście kwantowej teorii pola są to ścieżki relatywistycznie zlokalizowanych kwantów w formalizmie, który podąża ścieżkami poszczególnych cząstek. W kontekście czysto statystycznym ścieżki te nadal pojawiają się w matematycznej zgodności z polami kwantowymi, ale ich interpretacja jest mniej bezpośrednio fizyczna.

Reprezentacja całkowa natychmiast pokazuje, że G ( r ) jest dodatnie, ponieważ jest reprezentowane jako ważona suma dodatnich gaussów. Podaje również szybkość zaniku przy dużym r, ponieważ właściwy czas na osiągnięcie przez błądzenie losowe pozycji τ wynosi r ² iw tym czasie wysokość Gaussa zmniejszyła się o . Współczynnik zaniku odpowiedni dla pozycji r wynosi zatem . ${\ Displaystyle e ^ {-t \ tau} = e ^ {-tr ^ {2}}}$${\ Displaystyle e ^ {- {\ sqrt {t}} r}}$

Przybliżenie heurystyczne dla G ( r ) to:

${\ Displaystyle G (r) \ około {e ^ {- {\ sqrt {t}} r} \ ponad r ^ {d-2}}}$

Nie jest to dokładna forma, z wyjątkiem trzech wymiarów, gdzie interakcje między ścieżkami stają się ważne. Dokładne formy w dużych wymiarach są wariantami funkcji Bessela .

Interpretacja polimeru Symanzik

Interpretacja korelacji jako kwanty o stałym rozmiarze przemieszczające się wzdłuż losowych spacerów pozwala zrozumieć, dlaczego krytyczny wymiar interakcji H ⁴ wynosi 4. Termin H ⁴ można traktować jako kwadrat gęstości spacerów losowych w dowolnym punkt. Aby taki termin zmieniał funkcje korelacji skończonego rzędu, które wprowadzają tylko kilka nowych losowych spacerów do zmiennego środowiska, nowe ścieżki muszą się przecinać. W przeciwnym razie kwadrat gęstości jest proporcjonalny do gęstości i przesuwa tylko współczynnik H ² o stałą. Ale prawdopodobieństwo przecięcia błądzeń losowych zależy od wymiaru, a błądzenia losowe w wymiarze wyższym niż 4 nie przecinają się.

Wymiar fraktalny zwykłego błądzenia losowego to 2. Liczbę kul wielkości ε wymagane na pokrycie podwyższenia ścieżkę ε ^-2 . Dwa obiekty o wymiarze fraktalnym 2 będą się przecinać z rozsądnym prawdopodobieństwem tylko w przestrzeni o wymiarze 4 lub mniejszym, tak samo jak w przypadku ogólnej pary płaszczyzn. Kurt Symanzik argumentował, że oznacza to, że krytyczne fluktuacje Isinga w wymiarach wyższych niż 4 powinny być opisywane przez pole swobodne. Ten argument ostatecznie stał się matematycznym dowodem.

4 −  wymiary ε – grupa renormalizacji

Model Isinga w czterech wymiarach jest opisany przez zmienne pole, ale teraz fluktuacje oddziałują na siebie. W reprezentacji polimeru przecięcia błądzeń losowych są marginalnie możliwe. W kontynuacji pola kwantowego, kwanty oddziałują.

Logarytm ujemny prawdopodobieństwa dowolnej konfiguracji pola H jest funkcją energii swobodnej

${\ Displaystyle F = \ int d ^ {4} x \ lewo [ {Z \ ponad 2} | \ nabla H | ^ {2} + {t \ ponad 2} H ^ {2} + {\ Lambda \ ponad 4 !}H^{4}\prawo]\,}$

Czynniki liczbowe służą uproszczeniu równań ruchu. Celem jest zrozumienie fluktuacji statystycznych. Jak każda inna niekwadratowa całka po torze, funkcje korelacji mają rozwinięcie Feynmana jako cząstki poruszające się wzdłuż losowych spacerów, dzieląc się i ponownie łącząc w wierzchołkach. Siła oddziaływania jest sparametryzowana przez klasycznie bezwymiarową wielkość λ.

Chociaż analiza wymiarowa pokazuje, że zarówno λ, jak i Z są bezwymiarowe, jest to mylące. Statystyczne fluktuacje długości fali nie są dokładnie niezmienne w skali i stają się niezmienne tylko wtedy, gdy zanika siła interakcji.

Powodem jest to, że istnieje odcięcie używane do zdefiniowania H , a odcięcie określa najkrótszą długość fali. Fluktuacje H przy długościach fal w pobliżu punktu odcięcia mogą wpływać na fluktuacje dłuższej długości fali. Jeśli system jest skalowany wraz z odcięciem, parametry będą skalowane przez analizę wymiarową, ale porównywanie parametrów nie powoduje porównania zachowania, ponieważ przeskalowany system ma więcej trybów. Jeśli system zostanie przeskalowany w taki sposób, że odcięcie dla krótkiej długości fali pozostanie stałe, fluktuacje długich długości fal zostaną zmodyfikowane.

Renormalizacja Wilsona

Szybkim heurystycznym sposobem badania skalowania jest odcięcie liczb falowych H w punkcie λ. Mody Fouriera H o liczbach falowych większych niż λ nie mogą podlegać fluktuacjom. Przeskalowanie długości, które zmniejsza cały system, zwiększa wszystkie liczby falowe i przesuwa pewne fluktuacje powyżej wartości odcięcia.

Aby przywrócić stary punkt odcięcia, wykonaj częściową integrację na wszystkich numerach falowych, które kiedyś były zabronione, ale teraz podlegają fluktuacjom. Na diagramach Feynmana całkowanie w trybie fluktuującym przy liczbie falowej k łączy w parach linie przenoszące pęd k w funkcji korelacji ze współczynnikiem propagatora odwrotnego.

W przypadku przeskalowania, gdy system jest zmniejszany o współczynnik (1+ b ), współczynnik t skaluje się o współczynnik (1+ b ) ^{2 na} podstawie analizy wymiarowej. Zmiana w t dla nieskończenie małego b wynosi 2 bt . Pozostałe dwa współczynniki są bezwymiarowe i w ogóle się nie zmieniają.

Efekt najniższego rzędu całkowania można obliczyć z równań ruchu:

${\ Displaystyle \ nabla ^ {2} H + tH = - {\ lambda \ ponad 6} H ^ {3}.}$

To równanie jest tożsamością wewnątrz dowolnej funkcji korelacji z dala od innych wstawek. Po scałkowaniu modów z Λ < k < (1+ b )Λ będzie to nieco inna identyczność.

Ponieważ postać równania zostaną zachowane, aby znaleźć zmiany współczynników jest ona wystarczająca do analizy zmian w H ³ czasie. W Feynman rozszerzalności diagramie H ³ warunek w funkcji korelacji wewnątrz korelacji ma trzy zwisające linie. Połączenie dwóch z nich przy dużej liczbie falowej k daje zmianę H ³ z jedną wiszącą linią, a więc proporcjonalną do H :

${\ Displaystyle \ delta H ^ {3} = 3 H \ int _ {\ Lambda < | k | < (1 + b) \ Lambda {d ^ {4} k \ ponad (2 \ pi) ^ {4}} {1 \ponad (k^{2}+t)}}$

Współczynnik 3 wynika z faktu, że pętlę można zamknąć na trzy różne sposoby.

Całkę należy podzielić na dwie części:

${\ Displaystyle \ int dk {1 \ nad k ^ {2}} - t \ int dk {1 \ nad k ^ {2} (k ^ {2} + t)} = A \ Lambda ^ {2} b + Bbt}$

Pierwsza część nie jest proporcjonalna do t , aw równaniu ruchu może być wchłonięta przez stałe przesunięcie w t . Jest to spowodowane faktem, że człon H ³ ma część liniową. Tylko drugi składnik, który zmienia się od t do t , przyczynia się do skalowania krytycznego.

Ten nowy wyraz liniowy dodaje się do pierwszego wyrazu po lewej stronie, zmieniając t o wartość proporcjonalną do t . Całkowita zmiana w t jest sumą wyrazu z analizy wymiarowej i tego drugiego wyrazu z iloczynów operatorowych :

${\ Displaystyle \ delta t = \ lewo (2-{B \ lambda \ ponad 2} \ po prawej) bt}$

Czyli t jest przeskalowany, ale jego wymiar jest nietypowy , zmienia się o wielkość proporcjonalną do wartości λ.

Ale λ też się zmienia. Zmiana λ wymaga uwzględnienia rozszczepienia się linii, a następnie szybkiego ponownego połączenia. Proces najniższego rzędu to taki, w którym jedna z trzech linii z H ³ dzieli się na trzy, które szybko łączą się z jedną z pozostałych linii z tego samego wierzchołka. Korekta wierzchołka to

${\ Displaystyle \ delta \ lambda = - {3 \ lambda ^ {2} \ ponad 2} \ int _ {k} dk {1 \ nad (k ^ {2} + t) ^ {2}} = - {3 \lambda ^{2} \over 2}b}$

Współczynnik liczbowy jest trzykrotnie większy, ponieważ przy wyborze, którą z trzech nowych linii należy skrócić, istnieje dodatkowy czynnik wynoszący trzy. Więc

${\ Displaystyle \ delta \ lambda = -3 B \ lambda ^ {2} b}$

Te dwa równania razem definiują równania grupy renormalizacji w czterech wymiarach:

${\ Displaystyle {\ zacząć {wyrównany} {dt \ nad t} i = \ lewo (2-{B \ lambda \ nad 2} \ po prawej) b \ \ {d \ lambda \ nad \ lambda} i = {-3 B \lambda \over 2}b\end{wyrównany}}}$

Współczynnik B jest określony wzorem

${\ Displaystyle Bb = \ int _ {\ Lambda <| k | < (1 + b) \ Lambda {d ^ {4} k \ ponad (2 \ pi) ^ {4} {1 \ ponad k ^ { 4}}}$

i jest proporcjonalna do pola trójwymiarowej kuli o promieniu λ, razy szerokość obszaru całkowania b Λ podzielona przez Λ ⁴ :

${\ Displaystyle B = (2 \ pi ^ {2} \ Lambda ^ {3}) {1 \ nad (2 \ pi) ^ {4}} {b \ Lambda} {1 \ nad b \ Lambda ^ {4} }={1 \ponad 8\pi ^{2}}}$

W innych wymiarach stała B zmienia się, ale ta sama stała pojawia się zarówno w przepływie t, jak iw przepływie sprzęgającym. Powodem jest to, że pochodną względem t zamkniętej pętli z jednym wierzchołkiem jest zamknięta pętla z dwoma wierzchołkami. Oznacza to, że jedyną różnicą między skalowaniem sprzężenia a t są czynniki kombinatoryczne z łączenia i rozdzielania.

Punkt stały Wilson-Fisher

Badanie trzech wymiarów, wychodząc od teorii czterowymiarowej, powinno być możliwe, ponieważ prawdopodobieństwa przecięcia przypadkowych spacerów zależą w sposób ciągły od wymiarowości przestrzeni. W języku grafów Feynmana sprzężenie nie zmienia się zbytnio przy zmianie wymiaru.

Proces kontynuacji odchodzenia od wymiaru 4 nie jest do końca dobrze zdefiniowany bez recepty, jak to zrobić. Recepta jest dobrze zdefiniowana tylko na diagramach. Zastępuje reprezentację Schwingera w wymiarze 4 reprezentacją Schwingera w wymiarze 4 − ε zdefiniowaną przez:

${\ Displaystyle G (xy) = \ int d \ tau {1 \ ponad t ^ {d \ ponad 2}} e ^ {{x ^ {2} \ ponad 2 \ tau} + t \ tau}}$

W wymiarze 4 − ε sprzęgło λ ma dodatni wymiar skali ε, który należy dodać do przepływu.

${\ Displaystyle {\ zacząć {wyrównany} {d \ lambda \ nad \ lambda} i = \ varepsilon -3B \ lambda \ \ {dt \ nad t} i = 2 \ lambda B \ koniec {wyrównany}}}$

Współczynnik B jest zależny od wymiaru, ale anuluje się. Punkt stały dla λ nie jest już zerem, ale przy:

${\ Displaystyle \ lambda = {\ varepsilon \ ponad 3B}}$

gdzie wymiary skali t są zmienione o wielkość λ B = ε/3.

Wykładnik namagnesowania zmienia się proporcjonalnie do:

${\ Displaystyle {\ tfrac {1} {2}} \ lewo (1-{\ varepsilon \ ponad 3} \ po prawej)}$

co wynosi 0,333 w 3 wymiarach (ε = 1) i 0,166 w 2 wymiarach (ε = 2). Nie jest to tak daleko od zmierzonego wykładnika 0,308 i dwuwymiarowego wykładnika Onsagera 0,125.

Nieskończone wymiary – pole średnie

Zachowanie modelu Isinga na w pełni połączonym grafie może być całkowicie zrozumiane przez teorię pola średniego . Ten rodzaj opisu jest odpowiedni dla bardzo wielkowymiarowych kratek kwadratowych, ponieważ wtedy każda lokalizacja ma bardzo dużą liczbę sąsiadów.

Chodzi o to, że jeśli każdy spin jest powiązany z dużą liczbą spinów, ważny jest tylko średni stosunek obrotów + do −, ponieważ wahania tej średniej będą niewielkie. Średni obszar H jest średnią frakcję obrotów, które + minus średni ułamek obrotów, które -. Koszt energetyczny odwrócenia pojedynczego spinu w średnim polu H wynosi ±2 JNH . Wygodnie jest przedefiniować J, aby zaabsorbować czynnik N , tak aby granica N → ∞ była gładka. Jeśli chodzi o nowy J , koszt energii potrzebny do odwrócenia rotacji wynosi ±2 JH .

Ten koszt energii daje stosunek prawdopodobieństwa p, że spin wynosi + do prawdopodobieństwa 1− p, że spin wynosi −. Ten stosunek jest współczynnikiem Boltzmanna:

${\ Displaystyle {p \ ponad 1 p} = e ^ {2 \ beta JH}}$

aby

${\ Displaystyle p = {1 \ ponad 1 + e ^ {-2 \ beta JH}}}$

Średnia wartość rotacji jest określona przez uśrednienie 1 i -1 z wagami p i 1 -  p , więc średnia wartość wynosi 2 p  - 1. Ale ta średnia jest taka sama dla wszystkich rotacji, a zatem jest równa H .

${\ Displaystyle H = 2p-1 = {1-e ^ {-2 \ beta JH} \ ponad 1 + e ^ {-2 \ beta JH}} = \ tanh (\ beta JH)}$

Rozwiązaniem tego równania są możliwe spójne pola średnie. Dla β J < 1 istnieje tylko jedno rozwiązanie przy H = 0. Dla większych wartości β istnieją trzy rozwiązania, a rozwiązanie przy H = 0 jest niestabilne.

Niestabilność oznacza, że ​​zwiększenie średniego pola nieco powyżej zera daje statystyczny ułamek obrotów o wartości +, który jest większy niż wartość średniego pola. Zatem średnie pole, które oscyluje powyżej zera, wytworzy jeszcze większe średnie pole i ostatecznie ustali się na stabilnym rozwiązaniu. Oznacza to, że dla temperatur poniżej wartości krytycznej β J = 1 model średniego pola Isinga przechodzi przemianę fazową w granicy dużego N .

Powyżej temperatury krytycznej fluktuacje H są tłumione, ponieważ średnie pole przywraca fluktuację do pola zerowego. Poniżej temperatury krytycznej średnie pole jest doprowadzane do nowej wartości równowagi, która jest albo dodatnim H, albo ujemnym H rozwiązaniem równania.

Dla β J = 1 + ε, tuż poniżej temperatury krytycznej, wartość H można obliczyć z rozwinięcia Taylora tangensa hiperbolicznego:

${\ Displaystyle H = \ tanh (\ beta JH) = (1 + \ varepsilon ) H- {(1 + \ varepsilon ) ^ {3} H ^ {3} \ ponad 3}}$

Dzieląc przez H, aby odrzucić niestabilne rozwiązanie przy H = 0, stabilne rozwiązania to:

${\ Displaystyle H = {\ sqrt {3 \ varepsilon}}}$

Spontaniczne namagnesowanie H rośnie w pobliżu punktu krytycznego pierwiastka kwadratowego ze zmiany temperatury. Dzieje się tak zawsze, gdy H można obliczyć z rozwiązania równania analitycznego, które jest symetryczne między wartościami dodatnimi i ujemnymi, co doprowadziło Landau do podejrzenia, że ​​wszystkie przejścia fazowe typu Isinga we wszystkich wymiarach powinny być zgodne z tym prawem.

Wykładnik średniego pola jest uniwersalny, ponieważ zmiany charakteru rozwiązań równań analitycznych są zawsze opisywane przez katastrofy w szeregu Taylora, który jest równaniem wielomianowym. Zgodnie z symetrią, równanie H musi mieć tylko nieparzyste potęgi H po prawej stronie. Zmiana β powinna tylko płynnie zmieniać współczynniki. Przejście ma miejsce, gdy współczynnik H po prawej stronie wynosi 1. W pobliżu przejścia:

${\ Displaystyle H = {\ częściowy (\ beta F) \ nad \ częściowy h} = (1 + A \ varepsilon) H + BH ^ {3} + \ cdots}$

Czymkolwiek są A i B , o ile żaden z nich nie jest dostrojony do zera, spontaniczne namagnesowanie będzie rosło jako pierwiastek kwadratowy z ε. Ten argument może zawieść tylko wtedy, gdy energia swobodna β F jest albo nieanalityczna, albo nieogólna w dokładnym β, w którym zachodzi przejście.

Jednak spontaniczne namagnesowanie w układach magnetycznych i gęstość gazów w pobliżu punktu krytycznego są mierzone bardzo dokładnie. Gęstość i namagnesowanie w trzech wymiarach mają taką samą zależność potęgową od temperatury w pobliżu punktu krytycznego, ale zachowanie z eksperymentów jest następujące:

${\ Displaystyle H \ propto \ varepsilon ^ {0,308}}$

Wykładnik jest również uniwersalny, ponieważ jest taki sam w modelu Isinga jak w doświadczalnym magnesie i gazie, ale nie jest równy wartości średniego pola. To była wielka niespodzianka.

Odnosi się to również w dwóch wymiarach, gdzie

${\ Displaystyle H \ propto \ varepsilon ^ {0,125}}$

Ale tam nie było niespodzianki, bo to przewidział Onsager .

Niskie wymiary – wirowanie blokowe

W trzech wymiarach szereg perturbacyjny z teorii pola jest rozwinięciem stałej sprzężenia λ, która nie jest szczególnie mała. Efektywny rozmiar sprzężenia w punkcie stałym wynosi jeden ponad współczynnik rozgałęzienia ścieżek cząstek, więc parametr rozszerzania wynosi około 1/3. W dwóch wymiarach parametr perturbacyjnej ekspansji wynosi 2/3.

Ale renormalizację można również produktywnie zastosować bezpośrednio do spinów, bez przechodzenia do średniego pola. Historycznie to podejście jest spowodowane Leo Kadanoffem i poprzedzało perturbacyjne rozszerzenie ε.

Pomysł polega na iteracyjnej integracji obrotów sieci, generując przepływ w sprzężeniach. Ale teraz sprzężenia są współczynnikami energii sieci. Fakt istnienia opisu kontinuum gwarantuje, że ta iteracja zbiegnie się do ustalonego punktu, gdy temperatura zostanie dostrojona do krytyczności.

Renormalizacja Migdala-Kadanoffa

Napisz dwuwymiarowy model Isinga z nieskończoną liczbą możliwych interakcji wyższego rzędu. Aby zachować symetrię odbicia spinu, tylko potęgi przyczyniają się do:

${\ Displaystyle E = \ suma _ {ij} J_ {ij} S_ {i} S_ {j} + \ suma J_ {ijkl} S_ {i} S_ {j} S_ {k} S_ {l} \ ldots.}$

Przez niezmienność translacji J _ij jest tylko funkcją ij. Dzięki przypadkowej symetrii obrotowej, w dużym i oraz j jego wielkość zależy tylko od wielkości dwuwymiarowego wektora i  −  j . Podobnie ograniczone są współczynniki wyższego rzędu.

Iteracja renormalizacji dzieli sieć na dwie części – spiny parzyste i spiny nieparzyste. Nieparzyste spiny odbywają się na nieparzystej szachownicy, a parzyste na parzystej szachownicy. Kiedy spiny są indeksowane według pozycji ( i , j ), strony nieparzyste to te z i  +  j nieparzyste, a parzyste te z i  +  j parzyste, a strony parzyste są połączone tylko z nieparzystymi.

Dwie możliwe wartości nieparzystych spinów zostaną zintegrowane przez zsumowanie obu możliwych wartości. Spowoduje to powstanie nowej funkcji darmowej energii dla pozostałych równomiernych obrotów, z nowymi dostosowanymi sprzężeniami. Równomierne obroty są znowu w siatce, z osiami nachylonymi pod kątem 45 stopni w stosunku do starych. Odwrócenie systemu przywraca starą konfigurację, ale z nowymi parametrami. Te parametry opisują interakcję między spinami na większych odległościach . ${\displaystyle \scriptstyle {\sqrt {2}}}$

Zaczynając od modelu Isinga i powtarzając tę ​​iterację, ostatecznie zmienia się wszystkie sprzężenia. Gdy temperatura jest wyższa niż temperatura krytyczna, sprzężenia zbiegają się do zera, ponieważ spiny na dużych odległościach nie są skorelowane. Ale kiedy temperatura jest krytyczna, będą niezerowe współczynniki łączące spiny we wszystkich rzędach. Przepływ można przybliżyć, biorąc pod uwagę tylko kilka pierwszych warunków. Ten skrócony przepływ da coraz lepsze przybliżenia do krytycznych wykładników, gdy uwzględnianych jest więcej wyrazów.

Najprostszym przybliżeniem jest zachowanie tylko zwykłego wyrazu J i odrzucenie wszystkiego innego. Wygeneruje to przepływ w J , analogiczny do przepływu w t w stałym punkcie λ w rozwinięciu ε.

Aby znaleźć zmianę w J , rozważ czterech sąsiadów nieparzystego miejsca. To jedyne spiny, które z nim współdziałają. Mnożnikowy wkład do funkcji podziału z sumy nad dwiema wartościami spinu w miejscu nieparzystym wynosi:

${\ Displaystyle e ^ {J (N_ {+} -N_ {-})} + e ^ {J (N_ {-} -N_ {+})} = 2 \ cosh (J [N_ {+} -N_ { -}])}$

gdzie N _± to liczba sąsiadów, którzy są ±. Ignorując współczynnik 2, bezpłatny wkład energii z tej nieparzystej strony wynosi:

${\ Displaystyle F = \ log (\ cosh [J (N_ {+} -N_ {-})]).}$

Obejmuje to interakcje najbliższego sąsiada i następnego najbliższego sąsiada, zgodnie z oczekiwaniami, ale także interakcję czterospinową, którą należy odrzucić. Aby skrócić do interakcji najbliższych sąsiadów, weź pod uwagę, że różnica energii między wszystkimi spinami o tych samych i równych liczbach + i – wynosi:

${\ Displaystyle \ Delta F = \ ln (\ cosh [4J]).}$

Na podstawie sprzężeń najbliższych sąsiadów różnica energii między wszystkimi spinami równymi i przesuniętymi wynosi 8 J . Różnica energii pomiędzy wszystkimi spinami równymi i nieschodkowymi, ale z zerowym spinem netto, wynosi 4 J . Pomijając interakcje czterospinowe, rozsądnym obcięciem jest średnia z tych dwóch energii lub 6 J . Ponieważ każdy link przyczyni się do dwóch nieparzystych obrotów, prawidłowa wartość do porównania z poprzednim to o połowę niższa:

${\ Displaystyle 3J' = \ ln (\ cosh [4J]).}$

W przypadku małego J szybko dochodzi do sprzężenia zerowego. Duży przepływ J 's do dużych złączy. Wykładnik namagnesowania jest określany na podstawie nachylenia równania w ustalonym punkcie.

Warianty tej metody dają dobre przybliżenia liczbowe krytycznych wykładników, gdy uwzględnionych jest wiele terminów, zarówno w dwóch, jak i trzech wymiarach.

Aplikacje

Magnetyzm

Pierwotną motywacją modelu było zjawisko ferromagnetyzmu . Żelazo jest magnetyczne; po namagnesowaniu pozostaje namagnesowany przez długi czas w porównaniu z jakimkolwiek czasem atomowym.

W XIX wieku uważano, że pola magnetyczne są spowodowane prądami w materii, a Ampère postulował, że magnesy trwałe są powodowane przez stałe prądy atomowe. Ruch klasycznych naładowanych cząstek nie mógł jednak wyjaśnić stałych prądów, jak wykazał Larmor . Aby uzyskać ferromagnetyzm, atomy muszą mieć stałe momenty magnetyczne, które nie są spowodowane ruchem klasycznych ładunków.

Po odkryciu spinu elektronu stało się jasne, że magnetyzm powinien być spowodowany dużą liczbą elektronów wirujących w tym samym kierunku. Naturalnym było zapytać, skąd wszystkie elektrony wiedzą, w którym kierunku wirować, ponieważ elektrony po jednej stronie magnesu nie oddziałują bezpośrednio z elektronami po drugiej stronie. Mogą wpływać tylko na swoich sąsiadów. Model Isinga został zaprojektowany w celu zbadania, czy duża część elektronów może być zmuszona do wirowania w tym samym kierunku przy użyciu tylko lokalnych sił.

Gaz kratowy

Model Isinga można zreinterpretować jako model statystyczny ruchu atomów. Ponieważ energia kinetyczna zależy tylko od pędu, a nie od położenia, podczas gdy statystyka pozycji zależy tylko od energii potencjalnej, termodynamika gazu zależy tylko od energii potencjalnej dla każdej konfiguracji atomów.

Zgrubny model polega na uczynieniu czasoprzestrzeni siecią i wyobrażeniu sobie, że każda pozycja zawiera atom albo nie. Przestrzeń konfiguracji jest to, że niezależne bitów B _I , w którym każdy bit ma wartość 0 albo 1 zależnie od tego, czy stanowisko jest zajęte czy nie. Atrakcyjna interakcja zmniejsza energię dwóch pobliskich atomów. Jeśli przyciąganie występuje tylko między najbliższymi sąsiadami, energia zmniejsza się o -4 JB _i B _j na każdą zajętą ​​sąsiednią parę.

Gęstość atomów można kontrolować, dodając potencjał chemiczny , który jest mnożnikiem prawdopodobieństwa kosztu dodania jeszcze jednego atomu. Mnożnik prawdopodobieństwa można zreinterpretować jako wyrażenie addytywne w logarytmie – energia. Dodatkowa energia konfiguracji z atomami N zmienia się o μN . Koszt prawdopodobieństwa jeszcze jednego atomu jest współczynnikiem exp(− βμ ).

Zatem energia gazu sieciowego wynosi:

${\ Displaystyle E = - {\ Frac {1} {2}} \ suma _ {\ langle ja, j \ rangle} 4JB_ {i} B_ {j} + \ suma _ {i} \ mu B_ {i}}$

Przepisywanie bitów pod kątem spinów, ${\ Displaystyle B_ {i} = (S_ {i} + 1) / 2.}$

${\ Displaystyle E = - {\ Frac {1} {2}} \ suma _ {\ langle ja, j \ rangle} JS_ {i} S_ {j} - {\ Frac {1} {2}} \ suma _ {i}(4J-\mu )S_{i}}$

Dla sieci, w których każda lokalizacja ma równą liczbę sąsiadów, jest to model Isinga z polem magnetycznym h = ( zJ  −  μ )/2, gdzie z jest liczbą sąsiadów.

W układach biologicznych zmodyfikowane wersje modelu gazu sieciowego zostały wykorzystane do zrozumienia szeregu zachowań wiązania. Obejmują one wiązanie ligandów z receptorami na powierzchni komórki, wiązanie białek chemotaksji z motorem wici oraz kondensację DNA.

Zastosowanie do neuronauki

Aktywność neuronów w mózgu można modelować statystycznie. Każdy neuron w dowolnym momencie jest aktywny + lub nieaktywny −. Aktywne neurony to te, które wysyłają potencjał czynnościowy w dół aksonu w dowolnym oknie czasowym, a nieaktywne to te, które tego nie robią. Ponieważ aktywność neuronowa w dowolnym momencie jest modelowana przez niezależne bity, Hopfield zasugerował, że dynamiczny model Isinga zapewniłby pierwsze przybliżenie sieci neuronowej, która jest zdolna do uczenia się .

Zgodnie z ogólnym podejściem Jaynesa, ostatnia interpretacja Schneidmana, Berry'ego, Segeva i Białeka jest taka, że ​​model Isinga jest użyteczny dla każdego modelu funkcji neuronowej, ponieważ model statystyczny aktywności neuronowej powinien być wybierany zgodnie z zasadą maksymalnej entropii . Biorąc pod uwagę kolekcję neuronów, model statystyczny, który może odtworzyć średnią szybkość odpalania dla każdego neuronu, wprowadza mnożnik Lagrange'a dla każdego neuronu:

${\ Displaystyle E = - \ suma _ {i} h_ {i} S_ {i}}$

Ale aktywność każdego neuronu w tym modelu jest statystycznie niezależna. Aby umożliwić korelacje par, gdy jeden neuron ma tendencję do odpalania (lub nie) wraz z innym, wprowadź pary mnożników lagrange:

${\ Displaystyle E = - {\ tfrac {1} {2}} \ suma _ {ij} J_ {ij} S_ {i} S_ {j} - \ suma _ {i} h_ {i} S_ {i}}$

gdzie nie są ograniczone do sąsiadów. Zauważ, że to uogólnienie modelu Isinga jest czasami nazywane kwadratowym wykładniczym rozkładem binarnym w statystyce. Ta funkcja energii wprowadza jedynie błędy prawdopodobieństwa dla spinu o wartości i dla pary spinów o tej samej wartości. Korelacje wyższego rzędu nie są ograniczone przez mnożniki. Wzór aktywności próbkowany z tego rozkładu wymaga największej liczby bitów do przechowania w komputerze, w najbardziej wydajnym schemacie kodowania, jaki można sobie wyobrazić, w porównaniu z jakimkolwiek innym rozkładem o tej samej średniej aktywności i korelacjach parami. Oznacza to, że modele Isinga są odpowiednie dla każdego systemu, który jest opisywany przez bity, które są jak najbardziej losowe, z ograniczeniami korelacji parami i średnią liczbą jedynek, co często występuje zarówno w naukach fizycznych, jak i społecznych. ${\ Displaystyle J_ {ij}}$

Okulary do wirowania

Za pomocą modelu Isinga można również opisać tak zwane szkła spinowe , za pomocą zwykłego hamiltonianu, w którym zmienne S opisują spiny Isinga, podczas gdy J _i,k są brane z rozkładu losowego. Dla szkieł spinowych typowy rozkład wybiera wiązania antyferromagnetyczne z prawdopodobieństwem p i wiązania ferromagnetyczne z prawdopodobieństwem 1 −  p . Wiązania te pozostają stałe lub „wygaszone” nawet w obecności wahań temperatury. Gdy p  = 0 mamy oryginalny model Isinga. Ten system sam w sobie zasługuje na zainteresowanie; szczególnie jeden ma właściwości „nieergodyczne” prowadzące do dziwnego zachowania relaksacyjnego. Dużo uwagi przyciągnął również powiązany model Isinga rozmycia więzi i miejsca, zwłaszcza w dwóch wymiarach, co prowadzi do intrygujących zachowań krytycznych. ${\ Displaystyle {\ kapelusz {H}} = - {\ Frac {1} {2}} \ \ sum J_ {i, k} \ S_ {i} \ S_ {k}}$

Lód morski

Przybliżenia stawu topliwego 2D można utworzyć za pomocą modelu Isinga; Dane dotyczące topografii lodu morskiego mają dość duży wpływ na wyniki. Zmienna stanu jest binarna dla prostego przybliżenia 2D, będącego albo wodą, albo lodem.

Zobacz też

Przypisy

Bibliografia

Zewnętrzne linki

• Model Isinga w The Net Advance of Physics
• Barry Arthur Cipra , „Model Isinga jest NP-zupełny ”, SIAM News , tom. 33, nr 6; wydanie online (.pdf)
• Artykuł w Science World na temat modelu Ising
• Dynamiczny aplet Java Ising 2D autorstwa UCSC
• Dynamiczny aplet Javy Ising 2D
• Większy/bardziej skomplikowany aplet Javy 2D Ising
• Symulacja Ising Model wykonana przez Enrique Zeleny, projekt Wolfram Demonstrations Project
• Przemiany fazowe na sieciach
• Trójwymiarowy dowód na istnienie modelu Isinga jest niemożliwy, twierdzi badacz z Sandii
• Interaktywna symulacja Monte Carlo modeli Ising, XY i Heisenberg z grafiką 3D (wymaga przeglądarki zgodnej z WebGL)
• Kod modelu Ising , przykład odszumiania obrazu za pomocą modelu Ising
• Dobrym wprowadzeniem są notatki z wykładu Davida Tonga
• Rysunkowy obraz magnesów, który zmienił naukę — artykuł w magazynie Quanta o modelu Ising