Równanie Debye'a-Hückla - Debye–Hückel equation

Chemicy Peter Debye i Erich Hückel zauważyli, że roztwory zawierające jonowe substancje rozpuszczone nie zachowują się idealnie nawet przy bardzo niskich stężeniach. Tak więc, podczas gdy stężenie substancji rozpuszczonych jest fundamentalne dla obliczenia dynamiki roztworu, wysunęli teorię, że dodatkowy czynnik, który nazwali gamma, jest niezbędny do obliczenia współczynników aktywności roztworu. Stąd oni opracował równanie Debye'a-Hückela i Debye'a-Hückela ograniczając prawo . Aktywność jest tylko proporcjonalna do stężenia i jest zmieniana przez czynnik znany jako współczynnik aktywności . Współczynnik ten uwzględnia energię interakcji jonów w roztworze. ${\ Displaystyle \ gamma}$

Prawo ograniczające Debye'a-Hückla

W celu obliczenia aktywności danego jonów C w roztworze trzeba znać stężenie i współczynnik aktywności: ${\displaystyle a_{C}}$

${\ Displaystyle a_ {C} = \ Gamma {\ Frac {[C]} {[C ^ {\ Ominus}]}},}$

gdzie

${\ Displaystyle \ gamma}$ jest współczynnikiem aktywności C,

${\ Displaystyle [C ^ {\ Ominus}]}$jest stężeniem wybranego stanu standardowego , np. 1 mol/kg, jeśli stosuje się molalność ,

${\displaystyle [C]}$ jest miarą stężenia C.

Dzielenie za pomocą daje ilość bezwymiarową. ${\displaystyle [C]}$${\ Displaystyle [C ^ {\ Ominus}]}$

Debye'a-Huckela prawo ograniczające pozwala na wyznaczenie współczynnika aktywności jonów w rozcieńczonym roztworze o znanej jonowej . Równanie to

${\ Displaystyle \ ln (\ gamma _ {i}) = - {\ Frac {z_ {i} ^ {2} q ^ {2} \ kappa {8 \ pi \ varepsilon _ {R} \ varepsilon _ {0 }k_{\text{B}}T}}=-{\frac {z_{i}^{2}q^{3}N_{\text{A}}^{1/2}}{4\pi (\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T)^{3/2}}}{\sqrt {10^{3}{\frac {I}{2}} }}=-Az_{i}^{2}{\sqrt {I}},}$

gdzie

${\displaystyle z_{i}}$jest liczbą ładunków jonów i ,

${\displaystyle q}$jest ładunek elementarny ,

${\ Displaystyle \ kappa}$jest odwrotnością długości ekranowania Debye'a (zdefiniowanej poniżej),

${\ Displaystyle \ varepsilon _ {r}}$jest względną przenikalnością rozpuszczalnika,

${\ Displaystyle \ varepsilon _ {0}}$to przenikalność elektryczna wolnej przestrzeni ,

${\displaystyle k_{\tekst{B}}}$jest stałą Boltzmanna ,

${\displaystyle T}$to temperatura roztworu,

${\ Displaystyle N_ {\ operatorka {A}}}$jest stałą Avogadro ,

${\ Displaystyle I}$jest siła jonowa roztworu (zdefiniowaną poniżej),

${\ Displaystyle A}$jest stałą zależną od temperatury. Jeśli jest wyrażony jako molalność, a nie molarność (jak w powyższym równaniu i w pozostałej części tego artykułu), to doświadczalna wartość wody wynosi 25 °C. Powszechnie używa się logarytmu dziesiętnego, w którym to przypadku rozkładamy , więc A jest . Mnożnik przed w równaniu dotyczy przypadku, gdy wymiary są . Gdy wymiary wynoszą , mnożnik należy usunąć z równania.${\ Displaystyle I}$${\ Displaystyle A}$ ${\ Displaystyle 1,172 {\ tekst {mol}} ^ {-1/2} \ tekst {kg}} ^ {1/2}}$${\ Displaystyle \ ln 10}$${\ Displaystyle 0.509 {\ tekst {mol}} ^ {-1/2} \ tekst {kg}} ^ {1/2}}$${\ Displaystyle 10 ^ {3}}$${\ Displaystyle I/2}$${\ Displaystyle I}$${\ Displaystyle {\ tekst {kret}} / {\ tekst {dm}} ^ {3}}$${\ Displaystyle I}$${\ Displaystyle {\ tekst {kret}} / {\ tekst {m}} ^ {3}}$${\ Displaystyle 10 ^ {3}}$

Należy zauważyć, że ponieważ jony w roztworze działają razem, współczynnik aktywności uzyskany z tego równania jest w rzeczywistości średnim współczynnikiem aktywności.

Nadmiar ciśnienia osmotycznego otrzymano z teorii Debye'a-Huckela jest CGS jednostek :

${\ Displaystyle P ^ {\ tekst {ex}} = - {\ Frac {k_ {\ tekst {B}} T \ kappa _ {\ tekst {cgs}} ^ {3}} {24 \ pi}} = - {\frac {k_{\text{B}}T\lewo({\frac {4\pi \sum _{j}c_{j}q_{j}}{\epsilon _{0}\epsilon _{r }k_{\text{B}}T}}\right)^{3/2}}{24\pi }}.}$

Dlatego ciśnienie całkowite jest sumą nadciśnienia osmotycznego i ciśnienia idealnego . Współczynnik osmotyczny następnie podaje ${\ Displaystyle P ^ {\ tekst {id}} = k_ {\ tekst {B}} T \ suma _ {i} c_ {i}}$

${\ Displaystyle \ phi = {\ Frac {P ^ {\ tekst {id}} + P ^ {\ tekst {ex}}} {P ^ {\ tekst {id}}}} = 1 + {\ Frac {P ^{\text{ex}}}{P^{\text{id}}}}.}$

Podsumowanie pierwszego artykułu Debye'a i Hückela na temat teorii rozcieńczonych elektrolitów

Angielski tytuł artykułu to „O teorii elektrolitów. I. Depresja punktu zamarzania i zjawiska pokrewne”. Pierwotnie została opublikowana w 1923 roku w tomie 24 niemieckojęzycznego czasopisma Physikalische Zeitschrift . Angielskie tłumaczenie tego artykułu znajduje się w księdze zebranych artykułów przedstawionych Debye'owi przez „jego uczniów, przyjaciół i wydawców z okazji jego siedemdziesiątych urodzin w dniu 24 marca 1954 roku”. Kolejne tłumaczenie na język angielski zostało ukończone w 2019 roku. Artykuł dotyczy obliczania właściwości roztworów elektrolitów znajdujących się pod wpływem pól elektrycznych indukowanych jonami, a więc zajmuje się elektrostatyką .

W tym samym roku po raz pierwszy opublikowali ten artykuł, Debye i Hückel, zwani dalej D&H, opublikowali również artykuł, który obejmował ich wstępną charakterystykę roztworów pod wpływem pól elektrycznych, zatytułowany „O teorii elektrolitów. II. Prawo ograniczające przewodnictwo elektryczne” , ale ten kolejny artykuł nie jest (jeszcze) tutaj omawiany.

W poniższym podsumowaniu (jeszcze niekompletnym i niesprawdzonym) użyto nowoczesnej notacji i terminologii, zarówno z chemii, jak i matematyki, aby uniknąć nieporozumień. Ponadto, z kilkoma wyjątkami w celu poprawy przejrzystości, podrozdziały w tym podsumowaniu są (bardzo) skróconymi wersjami tych samych podrozdziałów oryginalnego artykułu.

Wstęp

D&H zauważyć, że wzór Guldberga-Waage'a dla gatunków elektrolitów w równowadze reakcji chemicznej w postaci klasycznej jest

${\ Displaystyle \ prod _ {i = 1} ^ {s} x_ {i} ^ {\ nu _ {i}} = K}$

gdzie

${\displaystyle \textstyle \prod}$jest notacją mnożenia ,

${\displaystyle i}$jest fikcyjną zmienną wskazującą gatunek,

${\displaystyle s}$ to liczba gatunków biorących udział w reakcji,

${\displaystyle x_{i}}$to ułamek molowy gatunków ,${\displaystyle i}$

${\displaystyle \nu_{i}}$jest współczynnikiem stechiometrycznym gatunków ,${\displaystyle i}$

K jest stałą równowagi .

D & H że, ze względu na „wzajemne sił elektrostatycznych pomiędzy jonów”, konieczne jest modyfikowanie równanie Guldberg-Waage zastępując z , gdzie jest ogólny współczynnik aktywności, a nie „specjalnych” współczynnik aktywności (odrębny współczynnik aktywności związana z każdym gatunkiem) – co jest używane we współczesnej chemii od 2007 roku. ${\ Displaystyle K}$${\ Displaystyle \ gamma K}$${\ Displaystyle \ gamma}$

Zależność między a współczynnikami aktywności specjalnej jest ${\ Displaystyle \ gamma}$${\ Displaystyle \ gamma _ {i}}$

${\ Displaystyle \ log (\ gamma ) = \ suma _ {i = 1} ^ {s} \ nu _ {i} \ log (\ gamma _ {i}).}$

Podstawy

D&H wykorzystuje swobodne entropie Helmholtza i Gibbsa i wyraża wpływ sił elektrostatycznych w elektrolicie na jego stan termodynamiczny. W szczególności podzielili większość potencjałów termodynamicznych na terminy klasyczne i elektrostatyczne: ${\ Displaystyle \ Phi}$${\ Displaystyle \ Xi}$

${\ Displaystyle \ Phi = S-{\ Frac {U} {T}} = - {\ Frac {A} {T}}}$

gdzie

${\ Displaystyle \ Phi}$jest wolna entropia Helmholtza ,

${\displaystyle S}$jest entropia ,

${\ Displaystyle U}$to energia wewnętrzna ,

${\displaystyle T}$jest temperatura ,

${\ Displaystyle A}$to energia swobodna Helmholtza .

D & H uzyskując całkowitą różnicę o co ${\ Displaystyle \ Phi}$

${\ Displaystyle d \ Phi = {\ Frac {P} {T}} \ dV + {\ Frac {U} {T ^ {2}}} \ dT}$

gdzie

${\displaystyle P}$jest ciśnienie ,

${\ Displaystyle V}$to objętość .

Z definicji różniczki całkowitej oznacza to, że

${\ Displaystyle {\ Frac {P} {T}} = {\ Frac {\ częściowy \ Phi} {\ częściowy V}}}$

${\ Displaystyle {\ Frac {U} {T ^ {2}}} = {\ Frac {\ częściowy \ Phi} {\ częściowy T}}}$

które są przydatne w dalszej części.

Jak wspomniano wcześniej, energia wewnętrzna jest podzielona na dwie części:

${\ Displaystyle U = U_ {k} + U_ {e}}$

gdzie

${\displaystyle k}$ wskazuje część klasyczną,

${\displaystyle e}$ wskazuje część elektryczną.

Podobnie wolna entropia Helmholtza jest również podzielona na dwie części:

${\ Displaystyle \ Phi = \ Phi _ {k} + \ Phi _ {e}.}$

Stan D&H, bez podawania logiki, że

${\ Displaystyle \ Phi _ {e} = \ int {\ Frac {U_ {e}} {T ^ {2}}} \ dT.}$

Wydawałoby się, że bez żadnego uzasadnienia

${\ Displaystyle \ Phi _ {e} = \ int {\ Frac {P_ {e}} {T}} \, dV + \ int {\ Frac {U_ {e}} {T ^ {2}}} \ dT .}$

Nie wspominając o tym konkretnie, D&H podaje później wymagane (powyżej) uzasadnienie, argumentując to , założenie, że rozpuszczalnik jest nieściśliwy. ${\ Displaystyle \ Phi _ {e} = \ Xi _ {e}}$

Definicja wolnej entropii Gibbsa to ${\ Displaystyle \ Xi}$

${\ Displaystyle \ Xi = S-{\ Frac {U + PV} {T}} = \ Phi - {\ Frac {PV} {T}} = - {\ Frac {G} {T}}}$

gdzie jest energia swobodna Gibbsa . ${\ Displaystyle G}$

D&H daje całkowitą różnicę as ${\ Displaystyle \ Xi}$

${\ Displaystyle d \ Xi = - {\ Frac {V} {T}} \ dP + {\ Frac {U + PV} {T ^ {2}}} \ dT.}$

W tym momencie D&H zauważa, że ​​dla wody zawierającej 1 mol na litr chlorku potasu (nominalne ciśnienie i temperatura nie są podane), ciśnienie elektryczne wynosi 20 atmosfer. Ponadto zauważają, że ten poziom ciśnienia daje względną zmianę objętości o 0,001. Dlatego zaniedbują zmianę objętości wody pod wpływem ciśnienia elektrycznego, pisanie ${\displaystyle P_{e}}$

${\ Displaystyle \ Xi = \ Xi _ {k} + \ Xi _ {e}}$

i umieścić

${\ Displaystyle \ Xi _ {e} = \ Phi _ {e} = \ int {\ Frac {U_ {e}} {T ^ {2}}} \ dT.}$

D&H twierdzi, że według Plancka klasyczna część wolnej entropii Gibbsa to

${\ Displaystyle \ Xi _ {k} = \ suma _ {i = 0} ^ {s} N_ {i} (\ xi _ {i}-k_ {\ tekst {B}} ln (x_ {i}})) ,}$

gdzie

${\displaystyle i}$ jest gatunkiem,

${\displaystyle s}$ to liczba różnych rodzajów cząstek w roztworze,

${\ Displaystyle N_ {i}}$to liczba cząstek gatunku i ,

${\ Displaystyle \ xi _ {i}}$jest swoistą dla cząstki entropią swobodną Gibbsa gatunku i ,

${\displaystyle k_{\tekst{B}}}$jest stałą Boltzmanna ,

${\displaystyle x_{i}}$jest ułamkiem molowym gatunku i .

Gatunek zero jest rozpuszczalnikiem. Definicja jest następująca, gdzie małe litery wskazują specyficzne dla cząstki wersje odpowiednich rozległych właściwości: ${\ Displaystyle \ xi _ {i}}$

${\ Displaystyle \ xi _ {i} = s_ {i} - {\ Frac {u_ {i} + Pv_ {i}} {T}}.}$

D&H tego nie mówi, ale forma funkcjonalna for może być wyprowadzona z funkcjonalnej zależności potencjału chemicznego składnika idealnej mieszaniny od jego ułamka molowego. ${\ Displaystyle \ Xi _ {k}}$

D&H zauważa, że ​​energia wewnętrzna roztworu jest obniżana przez oddziaływanie elektryczne jego jonów, ale tego efektu nie można określić za pomocą przybliżenia krystalograficznego dla odległości między różnymi atomami (pierwiastek sześcienny ze stosunku całkowitej objętości do liczba cząstek w objętości). Dzieje się tak, ponieważ w ciekłym roztworze występuje więcej ruchu termicznego niż w krysztale. Ruch termiczny ma tendencję do rozmazywania naturalnej sieci, która w przeciwnym razie zostałaby zbudowana przez jony. Zamiast tego D&H wprowadza koncepcję atmosfery jonowej lub chmury. Podobnie jak sieć krystaliczna, każdy jon wciąż próbuje otoczyć się przeciwnie naładowanymi jonami, ale w bardziej swobodny sposób; w niewielkiej odległości od jonów dodatnich istnieje większe prawdopodobieństwo znalezienia jonów ujemnych i odwrotnie. ${\ Displaystyle U}$

Energia potencjalna dowolnego roztworu jonów

Wymaga tego elektroneutralność rozwiązania

${\ Displaystyle \ suma _ {i = 1} ^ {s} N_ {i} z_ {i} = 0,}$

gdzie

${\ Displaystyle N_ {i}}$to całkowita liczba jonów gatunków i w roztworze,

${\displaystyle z_{i}}$jest ładowaną liczbą gatunków i .

Doprowadzenie jonu gatunku i , początkowo daleko, do punktu w chmurze jonów, wymaga energii oddziaływania w ilości , gdzie jest ładunkiem elementarnym , a jest wartością skalarnego pola potencjału elektrycznego w . Gdyby siły elektryczne były jedynym czynnikiem w grze, konfiguracja minimalnej energii wszystkich jonów zostałaby osiągnięta w konfiguracji gęsto upakowanej sieci. Jednak jony są ze sobą w równowadze termicznej i poruszają się stosunkowo swobodnie. W ten sposób są one posłuszne statystykom Boltzmanna i tworzą rozkład Boltzmanna . Gęstości liczbowe wszystkich gatunków są zmieniane w stosunku do ich masy (ogólnej średniej) przez odpowiedni współczynnik Boltzmanna , gdzie jest stałą Boltzmanna , a jest temperaturą. Tak więc w każdym punkcie chmury ${\displaystyle P}$${\displaystyle z_{i}q\varphi}$${\displaystyle q}$${\displaystyle \varphi}$${\displaystyle P}$ ${\displaystyle n_{i}}$${\displaystyle n_{i}^{0}}$ ${\ Displaystyle e ^ {- {\ Frac {z_ {i} q \ varphi} {k_ {\ tekst {B}} T}}}}$${\displaystyle k_{\tekst{B}}}$${\displaystyle T}$

${\ Displaystyle n_ {i} = {\ Frac {N_ {i}} {V}} e ^ {- {\ Frac {z_ {i} q \ varphi} {k_ {\ tekst {B}} T}}} =n_{i}^{0}e^{-{\frac {z_{i}q\varphi }{k_{\text{B}}T}}}.}$

Zauważ, że w nieskończonej granicy temperatury wszystkie jony są rozłożone równomiernie, bez względu na ich oddziaływania elektrostatyczne.

Gęstość ładunku jest związana z gęstością numer:

${\ Displaystyle \ rho = \ suma _ {i} z_ {i} qn_ {i} = \ suma _ {i} z_ {i} qn_ {i} ^ {0}e ^ {- {\ Frac {z_ {i }q\varphi }{k_{\text{B}}T}}}.}$

Łącząc ten wynik dla gęstości ładunku z równaniem Poissona z elektrostatyki, otrzymujemy postać równania Poissona-Boltzmanna :

${\ Displaystyle \ nabla ^ {2} \ varphi =- {\ Frac {\ rho} {\ varepsilon _ {R} \ varepsilon _ {0}}} = - \ suma _ {i} \ Frac {z_ {i }qn_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}}}e^{-{\frac {z_{i}q\varphi }{k_{\text{B}} T}}}.}$

Równanie to jest trudne do rozwiązania i nie jest zgodne z zasadą liniowej superpozycji zależności między liczbą ładunków a natężeniem pola potencjalnego. Został on rozwiązany przez szwedzkiego matematyka Thomasa Hakona Gronwalla i jego współpracowników fizykochemii VK La Mer i Karla Sandveda w artykule z 1928 roku z Physikalische Zeitschrift traktującym o rozszerzeniach teorii Debye'a-Huckela, które odwoływały się do rozszerzenia serii Taylora.

Jednakże, dla wystarczająco niskich stężeń jonów, można zastosować przybliżenie rozwinięcia szeregiem Taylora pierwszego rzędu dla funkcji wykładniczej ( for ) do stworzenia liniowego równania różniczkowego (Hamann, Hamnett i Vielstich. Electrochemistry. Wiley-VCH. rozdział 2.4. 2). D&H twierdzi, że to przybliżenie dotyczy dużych odległości między jonami, co jest równoznaczne z stwierdzeniem, że stężenie jest niskie. Wreszcie twierdzą bez dowodu, że dodanie większej liczby terminów w rozszerzeniu ma niewielki wpływ na ostateczne rozwiązanie. Zatem ${\ Displaystyle e ^ {x} \ około 1 + x}$${\displaystyle 0<x\ll 1}$

${\ Displaystyle - \ suma _ {i} {\ Frac {Z_ {i} Qn_ {i} ^ {0}} \ varepsilon _ {R} \ varepsilon _ {0}}} e ^ {- {\ Frac { z_{i}q\varphi }{k_{\text{B}}T}}}\ok -\sum _{i}{\frac {z_{i}qn_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}}}\left(1-{\frac {z_{i}q\varphi }{k_{\text{B}}T}}\right)=-\left(\ suma _{i}{\frac {z_{i}qn_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}}}-\sum _{i}{\frac {z_{ i}^{2}q^{2}n_{i}^{0}\varphi }{\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}}\right). }$

Równanie Poissona-Boltzmanna jest przekształcane do

${\ Displaystyle \ nabla ^ {2} \ varphi = \ suma _ {i} {\ Frac {z_ {i} ^ {2} q ^ {2} n_ {i} ^ {0} \ varphi {\ varepsilon _ {r}\varepsilon _{0}k_{\text{B}}T}},}$

ponieważ pierwsza suma wynosi zero z powodu elektroneutralności.

Wydziel potencjał skalarny i przypisz resztki, które są stałe, do . Niech też będzie siła jonowa roztworu: ${\ Displaystyle \ kappa ^ {2}}$${\ Displaystyle I}$

${\ Displaystyle \ kappa ^ {2} = \ suma _ {i} {\ Frac {z_ {i} ^ {2} q ^ {2} n_ {i} ^ {0}} {\ varepsilon _ {r} \ varepsilon _{0}k_{\text{B}}T}}={\frac {2Iq^{2}}{\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T} },}$

${\ Displaystyle I = {\ Frac {1} {2}} \ suma _ {i} z_ {i} ^ {2} n_ {i} ^ {0}.}$

Zatem równanie podstawowe sprowadza się do postaci równania Helmholtza :

${\ Displaystyle \ nabla ^ {2} \ varphi = \ kappa ^ {2} \ varphi.}$

Dziś nazywa się długością pokazu Debye'a . D&H uznają znaczenie tego parametru w swoim artykule i scharakteryzują go jako miarę grubości atmosfery jonowej, która jest podwójną warstwą elektryczną typu Gouy-Chapman. ${\ Displaystyle \ kappa ^ {-1}}$

Równanie można wyrazić we współrzędnych sferycznych , przyjmując za jakiś dowolny jon: ${\displaystyle r=0}$

${\ Displaystyle \ nabla ^ {2} \ varphi = {\ Frac {1} {R ^ {2}}} {\ Frac {\ częściowy} }{\ częściowy R}} \ lewo (r ^ {2} {\ Frac {\partial \varphi (r)}{\partial r}}\right)={\frac {\partial ^{2}\varphi (r)}{\częściowy r^{2}}}+{\frac { 2}{r}}{\frac {\częściowy \varphi (r)}{\częściowy r}}=\kappa ^{2}\varphi (r).}$

Równanie ma następujące ogólne rozwiązanie (pamiętaj, że jest to stała dodatnia): ${\ Displaystyle \ kappa}$

${\ Displaystyle \ varphi (r) = A {\ Frac {e ^ {- {\ sqrt {\ kappa ^ {2}}} r} {r}} + A '{\ Frac {e ^ {{\ sqrt {\kappa ^{2}}}r}}{2r{\sqrt {\kappa ^{2}}}}}=A{\frac {e^{-\kappa r}}{r}}+A' '{\frac {e^{\kappa r}}{r}}=A{\frac {e^{-\kappa r}}{r}},}$

gdzie , , i są stałymi nieokreślonymi ${\ Displaystyle A}$${\displaystyle A'}$${\ Displaystyle A''}$

Potencjał elektryczny wynosi zero w nieskończoności z definicji, więc musi wynosić zero. ${\ Displaystyle A''}$

W kolejnym kroku D&H zakłada, że ​​istnieje pewien promień , poza którym żadne jony w atmosferze nie mogą zbliżyć się do środka (ładunku) wydzielonego jonu. Ten promień może wynikać z fizycznego rozmiaru samego jonu, rozmiarów jonów w chmurze i wszelkich cząsteczek wody otaczających jony. Matematycznie traktują wyodrębniony jon jako ładunek punktowy, do którego nie można zbliżyć się w promieniu . ${\displaystyle a_{i}}$${\displaystyle a_{i}}$

Potencjał samego ładunku punktowego jest

${\ Displaystyle \ varphi _ {\ tekst {PC}} (r) = {\ Frac {1} {4 \ pi \ varepsilon _ {R} \ varepsilon _ {0}}} {\ Frac {z_ {i} q }{r}}.}$

D&H mówi, że całkowity potencjał wewnątrz kuli wynosi

${\ Displaystyle \ varphi _ {\ tekst {sp}} (r) = \ varphi _ {\ tekst {PC}} (r) + B_ {i} = {\ Frac {1} {4 \ pi \ varepsilon _ { r}\varepsilon _{0}}}{\frac {z_{i}q}{r}}+B_{i},}$

gdzie jest stałą reprezentującą potencjał dodany przez atmosferę jonową. Nie podano żadnego uzasadnienia bycia stałą. Można jednak zauważyć, że tak właśnie jest, biorąc pod uwagę, że każdy sferyczny rozkład ładunku statycznego podlega matematyce twierdzenia o powłoce . Twierdzenie o powłoce mówi, że na naładowane cząstki wewnątrz kuli (o dowolnym ładunku) nie działa żadna siła. Ponieważ zakłada się, że atmosfera jonowa jest (uśredniona w czasie) sferycznie symetryczna, z ładunkiem zmieniającym się w funkcji promienia , można ją przedstawić jako nieskończoną serię koncentrycznych powłok ładunkowych. Dlatego wewnątrz promienia atmosfera jonów nie wywiera żadnej siły. Jeśli siła wynosi zero, potencjał jest stałą (z definicji). ${\displaystyle B_{i}}$${\displaystyle B_{i}}$${\ Displaystyle r}$${\displaystyle a_{i}}$

W połączeniu modelu o ciągłym rozkładzie, który dał równanie Poissona-Boltzmanna oraz modelu ładunku punktowego, zakłada się, że na promieniu , istnieje ciągłość i jego pierwsza pochodna. Zatem ${\displaystyle a_{i}}$${\ Displaystyle \ varphi (r)}$

${\ Displaystyle \ varphi (a_ {i}) = A_ {i} {\ Frac {e ^ {-\ kappa a_ {i}}} {a_ {i}}} = {\ Frac {1} {4 \ pi \varepsilon _{r}\varepsilon _{0}}}{\frac {z_{i}q}{a_{i}}}+B_{i}=\varphi _{\text{sp}}(a_{ i}),}$

${\ Displaystyle \ varphi '(a_ {i}) = - {\ Frac {A_ {i} e ^ {- \ kappa a_ {i}} (1 + \ kappa a_ {i})} {a_ {i} ^ {2}}}=-{\frac {1}{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {z_{i}q}{a_{i}^{2} }}=\varphi _{\text{sp}}'(a_{i}),}$

${\ Displaystyle A_ {i} = {\ Frac {z_ {i} q} {4 \ pi \ varepsilon _ {R} \ varepsilon _ {0}}} {\ Frac {e ^ {\ kappa a_ {i}} }{1+\kappa a_{i}}},}$

${\ Displaystyle B_ {i} = - {\ Frac {z_ {i} q \ kappa {4 \ pi \ varepsilon _ {R} \ varepsilon _ {0}}} {\ Frac {1} {1+ \ kappa a_{i}}}.}$

Zgodnie z definicją elektrycznej energii potencjalnej energia potencjalna związana z wyodrębnionym jonem w atmosferze jonowej wynosi

${\ Displaystyle u_ {i} = z_ {i} qB_ {i} = - {\ Frac {z_ {i} ^ {2} q ^ {2} \ kappa {4 \ pi \ varepsilon _ {r} \ varepsilon _{0}}}{\frac {1}{1+\kappa a_{i}}}.}$

Zauważ, że wymaga to jedynie znajomości ładunku pojedynczego jonu i potencjału wszystkich innych jonów.

Aby obliczyć energię potencjalną całego roztworu elektrolitu, należy zastosować uogólnienie wielokrotnych ładunków dla elektrycznej energii potencjalnej:

${\ Displaystyle U_ {e} = {\ Frac {1} {2}} \ suma _ {i = 1} ^ {s} N_ {i} u_ {i} = - \ suma _ {i = 1} ^ { s}{\frac {N_{i}z_{i}^{2}}{2}}{\frac {q^{2}\kappa }{4\pi \varepsilon _{r}\varepsilon _{0 }}}{\frac {1}{1+\kappa a_{i}}}.}$

Dodatkowy człon elektryczny do potencjału termodynamicznego

Bezwymiarowość

Równanie różniczkowe jest gotowe do rozwiązania (jak wspomniano powyżej, równanie obowiązuje tylko dla niskich stężeń):

${\ Displaystyle {\ Frac {\ częściowy ^ {2} \ Varphi (r)} {\ częściowy R ^ {2}}} + {\ Frac {2} {R}} {\ Frac {\ częściowy \ Varphi (r )}{\partial r}}={\frac {Iq\varphi (r)}{\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}}=\kappa ^{2 }\varphi (r).}$

Użycie twierdzenia π Buckinghama w tym zagadnieniu daje następujące grupy bezwymiarowe:

${\ Displaystyle \ pi _ {1} = {\ Frac {q \ varphi (r)} {k_ {\ tekst {B}} T}} = \ Phi (R (R))}$

${\ Displaystyle \ pi _ {2} = \ varepsilon _ {r}}$

${\ Displaystyle \ pi _ {3} = {\ Frac {ak_ {\ tekst {B}} T \ varepsilon _ {0}} {q ^ {2}}}}$

${\ Displaystyle \ pi _ {4} = a ^ {3}ja}$

${\ Displaystyle \ pi _ {5} = Z_ {0}}$

${\ Displaystyle \ pi _ {6} = {\ Frac {r} {a}} = R (r).}$

${\ Displaystyle \ Phi}$nazywa się zredukowanym skalarnym polem potencjału elektrycznego. nazywa się zredukowanym promieniem. Istniejące grupy można ponownie połączyć, tworząc dwie inne bezwymiarowe grupy w celu podstawienia do równania różniczkowego. Pierwszym jest to, co można by nazwać kwadratem zmniejszonej długości odwrotnego przesiewania , . Drugi można nazwać zredukowanym centralnym ładunkiem jonowym (przez duże Z). Zauważ, że chociaż jest już bezwymiarowe, bez podstawienia podanego poniżej równanie różniczkowe nadal byłoby wymiarowe. ${\ Displaystyle R}$${\ Displaystyle (\ kappa a) ^ {2}}$${\displaystyle Z_{0}}$${\displaystyle z_{0}}$

${\ Displaystyle {\ Frac {\ pi _ {4}}{\ pi _ {2} \ pi _ {3}}} = {\ Frac {a ^ {2} q ^ {2} } {\ varepsilon _ {r}\varepsilon _{0}k_{\text{B}}T}}=(\kappa a)^{2}}$

${\ Displaystyle {\ Frac {\ pi _ {5}}{\ pi _ {2} \ pi _ {3}}} = {\ Frac {z_ {0}q ^ {2}} {4 \ pi a \ varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}}=Z_{0}}$

Aby uzyskać niewymiarowe równanie różniczkowe i warunki początkowe, użyj grup, aby wyeliminować na korzyść , następnie wyeliminować na korzyść , wykonując regułę łańcucha i zastępując , następnie wyeliminować na korzyść (nie jest wymagana żadna reguła łańcucha), a następnie wyeliminować na korzyść , a następnie wyeliminuj na korzyść . Otrzymane równania są następujące: ${\displaystyle \pi}$${\ Displaystyle \ varphi (r)}$${\ Displaystyle \ Phi (R (r))}$${\ Displaystyle R (r)}$${\ Displaystyle r}$${\ Displaystyle {R ^ {\ prime}} (r) = a}$${\ Displaystyle r}$${\ Displaystyle R}$${\ Displaystyle I}$${\ Displaystyle (\ kappa a) ^ {2}}$${\displaystyle z_{0}}$${\displaystyle Z_{0}}$

${\ Displaystyle {\ Frac {\ częściowy \ Phi (R)} {\ częściowy R}} {\ bigg |} _ {R = 1} = - Z_ {0}}$

${\ Displaystyle \ Phi (\ infty) = 0}$

${\ Displaystyle {\ Frac {\ częściowy ^ {2} \ Phi (R)} {\ częściowy R ^ {2}}} + {\ Frac {2} {R}} {\ Frac {\ częściowy \ Phi (R )}{\częściowy R}}=(\kappa a)^{2}\Phi (R).}$

W przypadku soli kuchennej w roztworze 0,01 M w temperaturze 25°C typowa wartość wynosi 0,0005636, podczas gdy typowa wartość wynosi 7,017, co podkreśla fakt, że w niskich stężeniach jest celem przybliżenia zerowego rzędu wielkości, takiego jak analiza zakłóceń . Niestety, ze względu na warunek brzegowy w nieskończoności, zaburzenia regularne nie działają. Ten sam warunek brzegowy uniemożliwia nam znalezienie dokładnego rozwiązania równań. Pojedyncza perturbacja może jednak działać. ${\ Displaystyle (\ kappa a) ^ {2}}$${\displaystyle Z_{0}}$${\ Displaystyle (\ kappa a) ^ {2}}$

Eksperymentalna weryfikacja teorii

Aby zweryfikować słuszność teorii Debye'a-Hückla, wypróbowano wiele metod eksperymentalnych, mierząc współczynniki aktywności: problem polega na tym, że musimy iść w kierunku bardzo wysokich rozcieńczeń. Typowymi przykładami są: pomiary prężności pary, temperatury zamarzania, ciśnienia osmotycznego (metody pośrednie) oraz pomiar potencjału elektrycznego w ogniwach (metoda bezpośrednia). Dążąc do wysokich rozcieńczeń, dobre wyniki uzyskano stosując płynne ogniwa membranowe, możliwe było zbadanie środowiska wodnego ^10-4 M i stwierdzono, że dla elektrolitów 1:1 (jako NaCl lub KCl) równanie Debye'a-Hückla jest całkowicie prawidłowo, ale dla elektrolitów 2:2 lub 3:2 można znaleźć ujemne odchylenie od prawa granicznego Debye-Hückel: to dziwne zachowanie można zaobserwować tylko w bardzo rozcieńczonym obszarze, aw bardziej skoncentrowanych obszarach odchylenie staje się dodatnie. Możliwe, że równanie Debye'a-Hückela nie jest w stanie przewidzieć tego zachowania z powodu linearyzacji równania Poissona-Boltzmanna, a może nie: badania nad tym rozpoczęto dopiero w ostatnich latach XX wieku, ponieważ zanim to się stało, Nie da się zbadać obszaru 10 ^-4 M, więc możliwe jest, że w ciągu najbliższych lat zrodzą się nowe teorie.

Rozszerzenia teorii

Zaproponowano szereg podejść, aby rozszerzyć ważność prawa na zakresy stężeń powszechnie spotykane w chemii

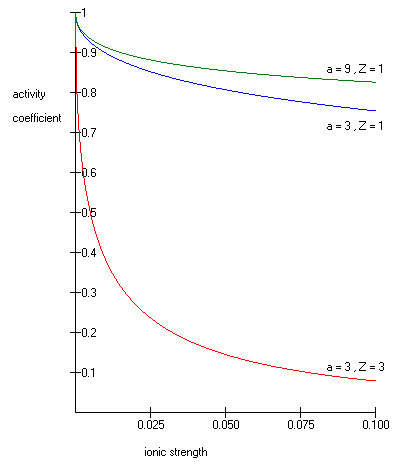
Jedno takie rozszerzone równanie Debye'a-Hückla jest podane przez:

${\ Displaystyle \ - \ log _ {10} (\ gamma) = {\ Frac {A | z_ {+} Z_ {-} | {\ sqrt {ja}}} {1 + Ba {\ sqrt {ja}} }}\,}$

gdzie w jego logarytm współczynnik aktywności, to ładunek całkowitą od jonu (1 dla H ⁺ , 2, Mg ^2+, etc.) jest siła jonowa wodnego roztworu, a to wielkość lub średnica efektywna z jon w angstremach . Efektywny promień hydratu jonu, a to promień jonu i jego ściśle związanych cząsteczek wody. Duże jony i mniej naładowane jony słabiej wiążą wodę i mają mniejsze promienie uwodnienia niż mniejsze, bardziej naładowane jony. Typowe wartości to 3Å dla jonów takich jak H ⁺ ,Cl ⁻ ,CN ⁻ i HCOO ⁻ . Efektywna średnica jonu hydroniowego wynosi 9 Å. i są stałymi o wartościach odpowiednio 0,5085 i 0,3281 w 25°C w wodzie. ${\ Displaystyle \ \ Gamma \,}$${\displaystyle \ z\,}$${\displaystyle \ ja\,}$${\displaystyle \ a\,}$${\displaystyle \A\,}$${\ Displaystyle \ B \,}$

Rozszerzone równanie Debye'a-Hückela zapewnia dokładne wyniki dla μ ≤ 0,1. W przypadku roztworów o większej sile jonowej należy stosować równania Pitzera . W tych rozwiązaniach współczynnik aktywności może faktycznie wzrastać wraz z siłą jonową.

Równania Debye'a-Hückla nie można stosować w roztworach surfaktantów, w których obecność miceli wpływa na właściwości elektrochemiczne układu (nawet zgrubna ocena przeszacowuje γ o ~50%).

Zobacz też

• Silny elektrolit
• Słaby elektrolit
• Atmosfera jonowa
• Teoria Debye'a-Hückla
• Równanie Poissona-Boltzmanna

Uwagi

Bibliografia

• P. Debye'a; E. Hückel (1923). "Zur Theorie der Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinungen" [Teoria elektrolitów. I. Obniżenie temperatury zamarzania i zjawiska pokrewne (PDF) . Physikalische Zeitschrift . 24 : 185–206.
• ^ Hamann, Hamnett i Vielstich (1998). Elektrochemia . Weinheim: Wiley-VCH Verlag GmbH. Numer ISBN 3-527-29096-6.CS1 maint: wiele nazwisk: lista autorów ( link )
• ^ Harris Daniel C. (2003). Ilościowa analiza chemiczna (wyd. 6). WH Freeman & Spółka. Numer ISBN 0-7167-4464-3.
• ^ Skoog, Douglas A. (lipiec 2003). Podstawy chemii analitycznej . Numer ISBN 0-534-41796-5.
• F. Malatesta, R. Zamboni. Aktywność i współczynniki osmotyczne z pola elektromagnetycznego płynnych komórek błonowych, VI - ZnSO4, MgSO4, CaSO4 i SrSO4 w wodzie o temperaturze 25°C. Journal of Solution Chemistry 1997, 26, 791–815

Zewnętrzne linki

• Aby łatwo obliczyć współczynniki aktywności w (nie micelarnych) roztworach, sprawdź otwarty projekt Aq-solutions IUPAC (bezpłatny) .
• Definicja złotej księgi