Gładkość - Smoothness

W analizy matematycznej The gładkość z funkcją jest właściwością mierzona liczbą ciągłych pochodnych ma ponad pewien domeny. Jako minimum funkcję można uznać za gładką, jeśli jest wszędzie różniczkowalna (a więc ciągła). Z drugiej strony może również posiadać pochodne wszystkich rzędów w swojej dziedzinie , w którym to przypadku mówi się, że jest nieskończenie różniczkowalna i określana jako funkcja (lub funkcja) C-nieskończoności . ${\displaystyle C^{\infty}}$

Klasy różniczkowalności

Klasa różniczkowalności to klasyfikacja funkcji według własności ich pochodnych . Jest to miara najwyższego rzędu pochodnej, która istnieje dla funkcji.

Rozważmy zbiór otwarty na linii rzeczywistej i funkcję f zdefiniowaną na tym zbiorze z wartościami rzeczywistymi. Niech k będzie nieujemną liczbą całkowitą . Mówi się, że funkcja f należy do klasy (różnicowalności) C ^k, jeśli pochodne f ′, f ″, ..., f ^{( k )} istnieją i są ciągłe . O funkcji f mówi się, że jest nieskończenie różniczkowalna , gładka lub klasy C ^∞ , jeśli ma pochodne wszystkich rzędów. Mówi się, że funkcja f należy do klasy C ^ω lub analityczna , jeśli f jest gładka i jeśli jej rozwinięcie w szereg Taylora wokół dowolnego punktu w jej dziedzinie jest zbieżne do funkcji w pewnym sąsiedztwie tego punktu. C ^ω jest więc ściśle zawarte w C ^∞ . Funkcje uderzeniowe są przykładami funkcji w C ^{∞ ,} ale nie w C ^ω .

Innymi słowy, klasa C ⁰ składa się ze wszystkich funkcji ciągłych. Klasa C ¹ składa się ze wszystkich funkcji różniczkowalnych, których pochodna jest ciągła; takie funkcje nazywane są ciągle różniczkowalne . Zatem funkcja C ¹ jest dokładnie funkcją, której pochodna istnieje i jest klasy C ⁰ . Ogólnie klasy C ^k można zdefiniować rekurencyjnie , deklarując C ⁰ jako zbiór wszystkich funkcji ciągłych i deklarując C ^k dla dowolnej dodatniej liczby całkowitej k jako zbioru wszystkich funkcji różniczkowalnych, których pochodna jest w C ^{k -1} . W szczególności, C ^k jest zawarte w C ^{k -1} dla każdego k > 0, i istnieją przykłady pokazujące, że to zawieranie jest ścisłe ( C ^k ⊊ C ^{k -1} ). Klasa C ^∞ funkcji nieskończenie różniczkowalnych, jest przecięciem klas C ^k gdy k zmienia się na nieujemnych liczbach całkowitych.

Przykłady

Funkcja

jest ciągła, ale nie różniczkowalna w x = 0 , więc należy do klasy C ⁰ , ale nie do klasy C ¹ .

Funkcja

jest różniczkowalna, z pochodną

Ponieważ oscyluje jako x → 0, nie jest ciągła przy zerze. Dlatego jest różniczkowalny, ale nie należy do klasy C ¹ . Co więcej, jeśli weźmiemy ( x ≠ 0) w tym przykładzie, można go użyć do wykazania, że ​​funkcja różniczkowalna funkcji różniczkowalnej może być nieograniczona na zbiorze zwartym, a zatem, że funkcja różniczkowalna na zbiorze zwartym nie może być lokalnie ciągły Lipschitz . ${\ Displaystyle \ cos (1/x)}$${\displaystyle g'(x)}$${\displaystyle g(x)}$${\ Displaystyle g (x) = x ^ {4/3} \ grzech (1/x)}$

Funkcje

gdzie k jest parzyste, są ciągłe i k razy różniczkowalne na wszystkich x . Ale przy x = 0 nie są one ( k + 1) razy różniczkowe, a więc należą do klasy C ^k , ale nie do klasy C ^{j ,} gdzie j > k .

Funkcja wykładnicza jest analityczna i dlatego należy do klasy C ^ω . Funkcje trygonometryczne są również analityczne, gdziekolwiek są zdefiniowane.

Funkcja uderzeniowa

jest gładka, a więc klasy C ^∞ , ale nie jest analityczna w x = ± 1 , a zatem nie należy do klasy C ^ω . Funkcja f jest przykładem funkcji gładkiej ze zwartą obsługą .

Klasy różniczkowalności wielowymiarowej

Funkcja określona w otwartym zestawu z mówi się z grupy w , do liczby całkowitej , jeśli wszystkie pochodne cząstkowe${\ Displaystyle f: U \ podzbiór \ mathbb {R} ^ {n} \ do \ mathbb {R}}$${\ Displaystyle U}$${\ Displaystyle \ mathbb {R} ^ {n}}$${\ Displaystyle C ^ {k}}$${\ Displaystyle U}$${\displaystyle k}$

istnieją i są ciągłe, dla wszystkich nieujemnych liczb całkowitych, takich jak , i każdy . Równoważnie jest klasy na jeśli -ty celu Fréchet pochodną o istnieje i w sposób ciągły w każdym punkcie . Mówi się, że funkcja jest klasy lub jest ciągła . ${\ Displaystyle \ alfa _ {1} \ alfa _ {2} \ ldots \ alfa _ {n}}$${\ Displaystyle \ alfa = \ alfa _ {1} + \ alfa _ {2} + \ cdots + \ alfa _ {n} \ równoważnik k}$${\ Displaystyle (r_ {1}, r_ {2}, \ ldots, r_ {n}) \ w U}$${\displaystyle f}$${\ Displaystyle C ^ {k}}$${\ Displaystyle U}$${\displaystyle k}$${\displaystyle f}$${\ Displaystyle U}$${\displaystyle f}$${\ Displaystyle C}$${\ Displaystyle C ^ {0}}$${\ Displaystyle U}$

Funkcja zdefiniowane w otwartym zestaw z , mówi się, że klasy na , na dodatnią liczbę całkowitą , gdy wszystkie składniki ${\ Displaystyle f: U \ podzbiór \ mathbb {R} ^ {n} \ do \ mathbb {R} ^ {m}}$${\ Displaystyle U}$${\ Displaystyle \ mathbb {R} ^ {n}}$${\ Displaystyle C ^ {k}}$${\ Displaystyle U}$${\displaystyle k}$

$${\ Displaystyle f_ {i} (x_ {1}, x_ {2}, \ ldots, x_ {n}) = (\ pi _ {i} \ circ f) (x_ {1}, x_ {2}, \ ldots ,x_{n})=\pi _{i}(f(x_{1},x_{2},\ldots ,x_{n})){\text{ dla }}i=1,2,3 ,\ldots ,m}$$

są klasy , gdzie są naturalne projekcje określone przez . Mówi się, że jest klasy lub jeśli jest ciągły, lub równoważnie, jeśli wszystkie składniki są ciągłe, na . ${\ Displaystyle C ^ {k}}$${\ Displaystyle \ pi _ {i}}$ ${\ Displaystyle \ pi _ {i}: \ mathbb {R} ^ {m} \ do \ mathbb {R}}$${\ Displaystyle \ pi _ {i} (x_ {1}, x_ {2}, \ ldots, x_ {m}) = x_ {i}}$${\ Displaystyle C}$${\ Displaystyle C ^ {0}}$${\displaystyle f_{i}}$${\ Displaystyle U}$

Przestrzeń C ^k funkcji

Niech D będzie otwartym podzbiorem prostej rzeczywistej. Zbiór wszystkich C ^k funkcji o wartościach rzeczywistych zdefiniowanych na D jest przestrzenią wektorową Frécheta z policzalną rodziną półnorm

$${\ Displaystyle p_ {K, m} = \ sup _ {x \ w K} \ lewo | f ^ {(m)} (x) \ prawo |}$$

gdzie K zmienia się w rosnącej sekwencji zbiorów zwartych, których sumą jest D , a m = 0, 1, ..., k .

Zbiór funkcji C ^∞ nad D również tworzy przestrzeń Frécheta. Używa się tych samych półnorm co powyżej, z wyjątkiem tego, że m może przekraczać wszystkie nieujemne wartości całkowite.

Powyższe przestrzenie występują naturalnie w aplikacjach, w których niezbędne są funkcje posiadające pochodne pewnych rzędów; jednak, szczególnie w badaniu równań różniczkowych cząstkowych , czasami bardziej owocna może być praca z przestrzeniami Sobolewa .

Ciągłość parametryczna

Określenia parametryczne ciągłości i ciągłości geometrycznej ( G ⁿ ) zostały wprowadzone Brian Barsky , aby pokazać, że gładkość krzywej może być mierzona przez usunięcie ograniczenia na szybkość , z jaką ślady parametrów na krzywej.

Ciągłość parametryczna to pojęcie stosowane do krzywych parametrycznych , które opisuje gładkość wartości parametru wraz z odległością wzdłuż krzywej.

Definicja

Mówi się, że krzywa (parametryczna) należy do klasy

C ^k , jeśli istnieje i jest ciągła w dniu , gdzie pochodne w punktach końcowych uważa się za pochodne jednostronne (tj. z prawej strony i z lewej). ${\ Displaystyle s: [0,1] \ do \ mathbb {R} ^ {n}}$${\ Displaystyle \ textstyle {\ Frac {d ^ {k} s} {dt ^ {k}}}}$${\displaystyle [0,1]}$${\ Displaystyle 0,1 \ w [0,1]}$${\ Displaystyle 0}$${\ Displaystyle 1}$

W praktycznym zastosowaniu tego pojęcia, krzywa opisująca ruch obiektu z parametrem czasu muszą C ¹ ciągłość i jej pierwsza pochodna jest różniczkowalną, na obiekt, który ma skończoną przyspieszenia. Aby uzyskać płynniejszy ruch, na przykład ruch kamery podczas kręcenia filmu, wymagane są wyższe rzędy ciągłości parametrycznej.

Porządek ciągłości

Dołączone dwa segmenty krzywej Béziera , które są tylko C ⁰ ciągłe

Dwa segmenty krzywej Béziera połączone w taki sposób, że są C ¹ ciągłe

Różne porządki ciągłości parametrycznej można opisać w następujący sposób:

• C ⁰ : zerowa pochodna jest ciągła (krzywe są ciągłe)
• C ¹ : zerowa i pierwsza pochodna są ciągłe
• C ² : zerowa, pierwsza i druga pochodna są ciągłe
• C ⁿ : od 0 do n pochodne są ciągłe

Ciągłość geometryczna

Krzywe z kontaktem G ¹ (okręgi,linia)

${\ Displaystyle (1-\ varepsilon ^ {2}) x ^ {2} -2px + ^ {2} = 0 \ p> 0 \ \ varepsilon \ geq 0}$
ołówek odcinków stożkowych z G ² -kontakt: p fix, zmienny ( : koło, : elipsa, : parabola, : hiperbola)${\displaystyle \varepsilon}$
${\ Displaystyle \ varepsilon = 0}$${\ Displaystyle \ varepsilon = 0,8}$${\ Displaystyle \ varepsilon =1}$${\ Displaystyle \ varepsilon = 1,2}$

Pojęcie ciągłości geometrycznej lub

ciągłości geometrycznej było stosowane przede wszystkim do przekrojów stożkowych (i pokrewnych kształtów) przez matematyków, takich jak Leibniz , Kepler i Poncelet . Koncepcja ta była wczesną próbą opisania, poprzez geometrię, a nie algebrę, koncepcji ciągłości wyrażonej za pomocą funkcji parametrycznej.

Podstawową ideą ciągłości geometrycznej było to, że pięć sekcji stożkowych to tak naprawdę pięć różnych wersji tego samego kształtu. Elipsy ma tendencję do koła jak mimośród zbliża się do zera lub do paraboli , gdy zbliża się on; a hiperbola skłania się do paraboli, gdy mimośród spada do jednego; może również mieć tendencję do przecinania się linii . W ten sposób zachowała się ciągłość między sekcjami stożkowymi. Te idee doprowadziły do ​​innych koncepcji ciągłości. Na przykład, jeśli okrąg i linia prosta byłyby dwoma wyrażeniami tego samego kształtu, być może linię można uznać za okrąg o nieskończonym promieniu . Aby tak się stało, należałoby zamknąć linię, pozwalając, by punkt był punktem na okręgu, i aby był identyczny. Takie idee były przydatne w tworzeniu nowoczesnej, zdefiniowanej algebraicznie, idei ciągłości funkcji i funkcji (więcej: projekcyjnie rozszerzona linia rzeczywista ). ${\displaystyle x=\infty}$${\displaystyle x=+\infty}$${\displaystyle x=\neg \infty}$${\displaystyle \infty}$

Gładkość krzywizn i powierzchni

Krzywa lub powierzchnia może być opisana jako posiadająca G ⁿ ciągłość z n zwiększający się miarą płynności. Rozważ segmenty po obu stronach punktu na krzywej:

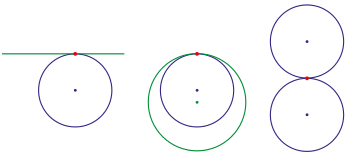
• G ⁰ : Krzywe stykają się w punkcie połączenia.
• G ¹ : Krzywe mają również wspólny kierunek stycznej w punkcie połączenia.
• G ² : Krzywe mają również wspólny środek krzywizny w punkcie połączenia.

Ogólnie, ciągłość G ⁿ istnieje, jeśli krzywe mogą być ponownie sparametryzowane tak, aby miały ciągłość C ⁿ (parametryczną). Reparametryzacja krzywej jest geometrycznie identyczna z oryginałem; dotyczy tylko parametru.

Równoważnie, dwie funkcje wektorowe f ( t ) i g ( t ) mają ciągłość G ^{n ,} jeśli f ^{( n )} ( t ) ≠ 0 i f ^{( n )} ( t ) ≡ kg ^{( n )} ( t ) , dla skalara k > 0 (tj. jeśli kierunek, ale niekoniecznie wielkość, dwóch wektorów jest równy).

Chociaż może to być oczywiste, że krzywa wymaga G ¹ ciągłość gładki na dobre estetykę takie jak dążył w architekturze i samochodów sportowych konstrukcji, wymagane są wyższe poziomy geometrycznej ciągłości. Na przykład, odbicia w karoserii nie pojawi się gładka, chyba że organ ma G ² ciągłość.

Zaokrąglony prostokąt (o dziewięćdziesiąt stopni łuku kołowego na czterech rogach) ma G ¹ ciągłości, ale nie ma G ² ciągłość. To samo dotyczy zaokrąglonego sześcianu z oktantami kuli w rogach i ćwierćwalcami wzdłuż krawędzi. Jeśli wymagana jest edytowalna krzywa z ciągłością G ² , zwykle wybierane są splajny sześcienne ; krzywe te są często wykorzystywane we wzornictwie przemysłowym .

Gładkość odcinkowo określonych krzywych i powierzchni

Inne koncepcje

Związek z analitycznością

Podczas gdy wszystkie funkcje analityczne są „gładkie” (tj. mają wszystkie pochodne ciągłe) na zbiorze, na którym są analityczne, przykłady takie jak funkcje wypukłości (wspomniane powyżej) pokazują, że odwrotność nie jest prawdziwa dla funkcji na rzeczywistych: istnieją gładkie rzeczywiste funkcje, które nie są analityczne. Proste przykłady funkcji, które są gładkie, ale nie analityczne w żadnym punkcie, mogą być wykonane za pomocą szeregów Fouriera ; innym przykładem jest funkcja Fabiusa . Choć mogłoby się wydawać, że takie funkcje są raczej wyjątkiem niż regułą, okazuje się, że funkcje analityczne są bardzo drobno rozrzucone wśród gładkich; bardziej rygorystycznie, funkcje analityczne tworzą skromny podzbiór funkcji gładkich. Co więcej, dla każdego otwartego podzbioru A linii rzeczywistej istnieją gładkie funkcje, które są analityczne na A i nigdzie indziej.

Przydatne jest porównanie sytuacji do sytuacji wszechobecności liczb transcendentalnych na linii rzeczywistej. Zarówno na prostej rzeczywistej, jak i na zbiorze funkcji gładkich, przykłady, które pojawiają się na pierwszy rzut oka (liczby algebraiczne/wymierne i funkcje analityczne) zachowują się znacznie lepiej niż większość przypadków: liczby przestępne i nigdzie funkcje analityczne nie mają pełnej miary. (ich uzupełnienia są skromne).

Opisana w ten sposób sytuacja jest w wyraźnym kontraście do złożonych funkcji różniczkowalnych. Jeśli złożona funkcja jest różniczkowalna tylko raz na zbiorze otwartym, jest zarówno nieskończenie różniczkowalna, jak i analityczna na tym zbiorze.

Gładkie partycje jedności

Funkcje gładkie z zadaną obsługą zamkniętą są używane w konstrukcji gładkich podziałów jedności (patrz podział jedności i słowniczek topologii ); są one niezbędne w badaniu gładkich rozmaitości , na przykład po to, by pokazać, że metryki riemannowskie mogą być definiowane globalnie, zaczynając od ich lokalnego istnienia. Prostym przypadkiem jest funkcja wypukłości na linii rzeczywistej, czyli gładka funkcja f, która przyjmuje wartość 0 poza przedział [ a , b ] i taka, że

Biorąc pod uwagę liczbę nakładających się przedziałów na linii, funkcje wypukłości mogą być konstruowane na każdym z nich oraz na przedziałach półnieskończonych i obejmują całą linię, tak aby suma funkcji była zawsze równa 1. ${\displaystyle (-\infty ,c]}$${\displaystyle [d,+\infty)}$

Z tego, co właśnie zostało powiedziane, podziały jedności nie mają zastosowania do funkcji holomorficznych ; ich odmienne zachowanie w stosunku do istnienia i kontynuacji analitycznej jest jednym z korzeni teorii snopów . W przeciwieństwie do tego, snopy o gładkich funkcjach zwykle nie przenoszą zbyt wielu informacji topologicznych.

Płynne funkcje na i między rozmaitościami

Ze względu na gładką rurę rozgałęźną , wymiaru i an Atlas czym mapa jest gładka na jeżeli wszystkim istnieje wykres taki sposób, że i jest gładki funkcji z sąsiedztwie w celu (wszystkie pochodne cząstkowe się do danego celu jest ciągły). Gładkość można sprawdzić w odniesieniu do dowolnego wykresu atlasu, który zawiera, ponieważ wymagania dotyczące płynności w funkcjach przejścia między wykresami zapewniają, że jeśli jest gładka w pobliżu na jednym wykresie, będzie gładka w pobliżu na dowolnym innym wykresie. ${\ Displaystyle M}$${\displaystyle m,}$ ${\ Displaystyle {\ mathfrak {U}} = \ {(U_ {\ alfa}, \ _ {\ alfa}) \} _ {\ alfa},}$${\ Displaystyle f: M \ do \ mathbb {R} }$${\ Displaystyle M}$${\ Displaystyle p \ w M}$${\displaystyle (U,\phi)\in {\mathfrak {U}}}$${\displaystyle p\w U,}$${\ Displaystyle f \ circ \ phi ^ {-1}: \ phi (U) \ do \ mathbb {R}}$${\ Displaystyle \ phi (p)}$${\ Displaystyle \ mathbb {R} ^ {m}}$${\ Displaystyle \ mathbb {R}}$${\displaystyle p,}$${\displaystyle f}$${\displaystyle p}$${\displaystyle p}$

Jeżeli jest mapą od do wielowymiarowej rozmaitości , to jest gładka jeżeli, dla każdego istnieje wykres zawierający i wykres zawierający takie, że i jest gładką funkcją z${\ Displaystyle F: M \ do N}$${\ Displaystyle M}$${\ Displaystyle n}$${\ Displaystyle N}$${\ Displaystyle F}$${\displaystyle p\w m}$${\displaystyle (U,\phi)}$${\displaystyle p,}$${\displaystyle (V,\psi)}$${\ Displaystyle F (p)}$${\ Displaystyle F (U) \ podzbiór V}$${\ Displaystyle \ psi \ circ F \ circ \ phi ^ {-1}: \ phi (U) \ do \ psi (V)}$${\ Displaystyle \ mathbb {R} ^ {n}.}$

Gładkie odwzorowania między rozmaitościami indukują liniowe odwzorowania między przestrzeniami stycznymi : dla , w każdym punkcie wektory styczne (lub różniczkowe) odwzorowują wektory styczne na wektorach stycznych w : a na poziomie wiązki stycznej , przesunięcie do przodu jest homomorfizmem wiązki wektorowej : Podwójny do przodu jest wycofywanie , które „ciągnie” kowektory z powrotem do kowektorów na i -form do -form: W ten sposób gładkie funkcje między rozmaitościami mogą przenosić dane lokalne , takie jak pola wektorowe i formy różniczkowe , z jednej rozmaitości do drugiej lub aż do przestrzeni euklidesowej, gdzie obliczenia takie jak integracja są dobrze rozumiane. ${\ Displaystyle F: M \ do N}$${\displaystyle p}$${\ Displaystyle F (p)}$${\ Displaystyle F_ {*, p}: T_ {p} M \ do T_ {F (p)} N}$${\ Displaystyle F_ {*}: TM \ do TN.}$${\ Displaystyle N}$${\displaystyle M}$${\displaystyle k}$${\displaystyle k}$${\ Displaystyle F ^ {*}: \ Omega ^ {k} (N) \ do \ Omega ^ {k} (M).}$

Preobrazy i postępy wzdłuż funkcji gładkich nie są na ogół rozmaitościami bez dodatkowych założeń. Preobrazy punktów regularnych (to znaczy, jeśli różnica nie znika na obrazie wstępnym) są rozmaitościami; to jest twierdzenie o obrazie wstępnym . Podobnie, posuwanie się do przodu wzdłuż osadzeń jest rozmaitością.

Funkcje gładkie między podzbiorami rozmaitości

Istnieje odpowiednie pojęcie gładkiego odwzorowania dla dowolnych podzbiorów rozmaitości. If jest funkcją, której dziedzina i zakres są podzbiorami rozmaitości i odpowiednio. mówi się, że jest gładka, jeśli dla wszystkich istnieje otwarty zestaw z i gładką funkcją, taką, że dla wszystkich${\displaystyle f:X\do Y}$${\displaystyle X\subseteq M}$${\ Displaystyle Y \ podzbiór N}$${\displaystyle f}$${\ Displaystyle x \ w X}$${\displaystyle U\subseteq M}$${\ Displaystyle x \ w U}$${\ Displaystyle F: U \ do N}$${\ Displaystyle F (p) = f (p)}$${\ Displaystyle p \ w U \ czapka X.}$

Zobacz też

• Nieciągłość
• lemat Hadamarda
• Nieanalityczna funkcja gładka  – Funkcje matematyczne, które są gładkie, ale nie analityczne
• Funkcja quasi-analityczna
• Osobliwość (matematyka)  – Punkt, w którym funkcja, krzywa lub inny obiekt matematyczny nie zachowuje się regularnie
• Sinuosity  - Stosunek długości łuku i odległości w linii prostej między dwoma punktami w funkcji falowej
• Płynny schemat
• Gładka liczba (teoria liczb)
• Wygładzanie
• Klin

Bibliografia