Metryka Kerra — Kerr metric

Ogólna teoria względności
${\ Displaystyle G_ {\ mu \ nu} + \ Lambda g_ {\ mu \ nu} = {8 \ pi G \ nad c ^ {4}} T_ {\ mu \ nu}}$
Wstęp Historia Sformułowanie matematyczne Testy
Idee fundamentalne Zasada równoważności Szczególna teoria względności Linia światowa Rozmaitość pseudo-Riemanna
Zjawiska Problem Keplera Soczewkowanie grawitacyjne Fale grawitacyjne Przeciąganie ramek Efekt geodezyjny Horyzont zdarzeń Osobliwość Czarna dziura Czas, przestrzeń Diagramy czasoprzestrzeni Czasoprzestrzeń Minkowskiego Most Einsteina-Rosena
Równania Formalizmy Równania Zlinearyzowana grawitacja Równania pola Einsteina Friedmann Geodezja Mathisson–Papapetrou–Dixon Hamilton-Jacobi-Einstein Formalizmy ADM BSSN Post-Newtonowski Zaawansowana teoria Teoria Kaluzy-Kleina Grawitacja kwantowa
Rozwiązania Schwarzschild ( wnętrze ) Reissner-Nordström Godel Kerra Kerr–Newman Kasner Lemaître–Tolman Taub-NUT Milne Robertson-Walker pp-fala kurz van Stockum Weyl-Lewis-Papapetrou
Naukowcy Einstein Lorentz Hilbert Poincaré Schwarzschilda de Sitter Reissner Nordström Weyl Eddington Friedman Milne Zwicky Lemaître Godel Kołodziej Robertson Bardeen Piechur Kerra Chandrasekhar Ehlers Penrose Hawking Rachaudhuri Taylor Hulse van Stockum Taub Nowy człowiek Yau Thorne inni
Portal fizyczny  Kategoria
v T mi

Metryki Kerr i geometria Kerr opisano geometrię pustej czasoprzestrzeni wokół obracającej się naładowanej osiowo symetryczny czarną dziurę z quasispherical horyzontu zdarzeń . The Kerr metryka jest dokładne rozwiązanie z Równanie Einsteina w ogólnej teorii względności ; równania te są wysoce nieliniowe , co sprawia, że ​​bardzo trudno jest znaleźć dokładne rozwiązania.

Przegląd

Metryka Kerra jest uogólnieniem na obracające się ciało metryki Schwarzschilda , odkrytej przez Karla Schwarzschilda w 1915 roku, która opisuje geometrię czasoprzestrzeni wokół nienaładowanego, sferycznie symetrycznego i nie obracającego się ciała. Odpowiednie rozwiązanie dla naładowanego , kulistego, nieobrotowego ciała, metryka Reissner-Nordström , została odkryta wkrótce potem (1916-1918). Jednak dokładne rozwiązanie dla nienaładowanej, obracającej się czarnej dziury, metryka Kerra, pozostawała nierozwiązana do 1963 roku, kiedy to odkrył Roy Kerr . Niedługo potem, w 1965 roku, odkryto naturalne rozszerzenie naładowanej, obracającej się czarnej dziury, metrykę Kerra-Newmana . Te cztery powiązane rozwiązania można podsumować w poniższej tabeli:

gdzie Q reprezentuje ładunek elektryczny ciała, a J reprezentuje jego spinowy moment pędu .

Zgodnie z metryką Kerra, obracające się ciało powinno wykazywać przeciąganie klatek (znane również jako precesja Lense-Thirring ), charakterystyczne przewidywanie ogólnej teorii względności. Pierwszy pomiar tego efektu przeciągania ramy został wykonany w 2011 roku w eksperymencie Gravity Probe B. Z grubsza rzecz biorąc, efekt ten przewiduje, że obiekty zbliżające się do obracającej się masy będą zaangażowane w jej obrót, nie z powodu przyłożonej siły lub momentu obrotowego, które można odczuć, ale raczej z powodu wirującej krzywizny samej czasoprzestrzeni związanej z obracającymi się ciałami . W przypadku obracającej się czarnej dziury, w wystarczająco bliskiej odległości, wszystkie obiekty – nawet światło – muszą obracać się wraz z czarną dziurą; region, w którym to się dzieje, nazywa się ergosferą .

Światło z odległych źródeł może ominąć horyzont zdarzeń kilka razy (jeśli jest wystarczająco blisko); tworzenie wielu obrazów tego samego obiektu . Dla odległego widza pozorna prostopadła odległość między obrazami zmniejsza się ze współczynnikiem e ^{2 π} (około 500). Jednak szybko wirujące czarne dziury mają mniejszą odległość między obrazami wielokrotności.

Obracające się czarne dziury mają powierzchnie, na których metryka wydaje się mieć widoczne osobliwości ; wielkość i kształt tych powierzchni zależy od masy czarnej dziury i momentu pędu . Zewnętrzna powierzchnia otacza ergosferę i ma kształt zbliżony do spłaszczonej kuli. Wewnętrzna powierzchnia wyznacza horyzont zdarzeń ; przedmioty przechodzące do wnętrza tego horyzontu nigdy już nie będą mogły komunikować się ze światem poza tym horyzontem. Jednak żadna powierzchnia nie jest prawdziwą osobliwością, ponieważ ich pozorną osobliwość można wyeliminować w innym układzie współrzędnych . Jak wspomniano powyżej, obiekty pomiędzy tymi dwiema powierzchniami muszą obracać się wraz z obracającą się czarną dziurą; ta cecha może w zasadzie zostać wykorzystana do wydobycia energii z obracającej się czarnej dziury, aż do jej niezmiennej energii masy Mc ² .

Eksperyment LIGO, który po raz pierwszy wykrył fale grawitacyjne, ogłoszony w 2016 r., zapewnił również pierwszą bezpośrednią obserwację pary czarnych dziur Kerra.

Metryczny

Metryka Kerra jest powszechnie wyrażana w jednej z dwóch form, formie Boyera-Lindquista i formie Kerra-Schilda. Można go łatwo wyprowadzić z metryki Schwarzschilda, stosując algorytm Newmana-Janisa przez formalizm Newmana-Penrose'a (znany również jako formalizm współczynnika spinowego), równanie Ernsta lub transformację współrzędnych elipsoidy.

Współrzędne Boyera-Lindquista

Metryka Kerra opisuje geometrię czasoprzestrzeni w sąsiedztwie masy obracającej się z momentem pędu . Metryka (lub równoważnie jej element liniowy dla właściwego czasu ) we współrzędnych Boyer-Lindquist jest ${\ Displaystyle M}$ ${\ Displaystyle J}$

${\ Displaystyle {\ zacząć {wyrównany} ds ^ {2} & = - c ^ {2} d \ tau ^ {2} \ \ & = - \ lewo (1 - {\ Frac {R_ {s} r} { \Sigma }}\right)c^{2}dt^{2}+{\frac {\Sigma }{\Delta }}dr^{2}+\Sigma d\theta ^{2}+\left(r ^{2}+a^{2}+{\frac {r_{s}ra^{2}}{\Sigma }}\sin ^{2}\theta \right)\sin ^{2}\theta \ d\phi ^{2}-{\frac {2r_{s}ra\sin ^{2}\theta }{\Sigma }}cdt\,d\phi \end{aligned}}}$

( 1 )

gdzie współrzędne są standardowymi spłaszczonymi współrzędnymi sferoidalnymi , które są równoważne współrzędnym kartezjańskim ${\displaystyle r,\theta,\phi}$

${\ Displaystyle x = {\ sqrt {r ^ {2} + a ^ {2}}} \ sin \ theta \ cos \ phi}$

( 2 )

${\ Displaystyle y = {\ sqrt {r ^ {2} + a ^ {2}}} \ sin \ theta \ sin \ phi}$

( 3 )

${\displaystyle z=r\cos\theta,}$

( 4 )

gdzie jest promień Schwarzschilda?${\displaystyle r_{s}}$

${\ Displaystyle R_ {s} = {\ Frac {2GM} {c ^ {2}}}}$

( 5 )

i gdzie dla zwięzłości, skale długości i zostały wprowadzone jako ${\displaystyle a\sigma}$${\ Displaystyle \ Delta}$

${\ Displaystyle a = {\ Frac {J} {Mc}},}$

( 6 )

${\ Displaystyle \ Sigma = r ^ {2} + a ^ {2} \ cos ^ {2} \ teta}$

( 7 )

${\ Displaystyle \ Delta = r ^ {2} - r_ {s} r + a ^ {2}.}$

( 8 )

Kluczową cechą, którą należy zauważyć w powyższej metryce, jest termin krzyżowy. Oznacza to, że istnieje sprzężenie między czasem i ruchem w płaszczyźnie obrotu, które znika, gdy moment pędu czarnej dziury spada do zera. ${\displaystyle dt\,d\phi.}$

W nierelatywistycznej granicy, gdzie (lub równoważnie, ) dochodzi do zera, metryka Kerra staje się metryką ortogonalną dla spłaszczonych współrzędnych sferoidalnych${\ Displaystyle M}$${\displaystyle r_{s}}$

${\ Displaystyle g \ mathop {\ longrightarrow } _ {M \ do 0} -c ^ {2} dt ^ {2} + {\ Frac {\ Sigma} {r ^ {2} + a ^ {2}}} dr^{2}+\Sigma d\theta ^{2}+\left(r^{2}+a^{2}\right)\sin ^{2}\theta d\phi ^{2}}$

( 9 )

Współrzędne Kerra-Schilda

Metryka Kerra może być wyrażona w postaci „Kerr-Schild” przy użyciu określonego zestawu współrzędnych kartezjańskich w następujący sposób. Rozwiązania te zostały zaproponowane przez Kerra i Schilda w 1965 roku.

${\ Displaystyle g_ {\ mu \ nu } = \ eta _ {\ mu \ nu} + fk_ {\ mu} k_ {\ nu} \!}$

( 10 )

${\ Displaystyle f = {\ Frac {2GMr ^ {3}} {r ^ {4} + a ^ {2} z ^ {2}}}}$

( 11 )

${\ Displaystyle \ mathbf {k} = (k_ {x}, k_ {y}, k_ {z}) = \ lewo ({\ Frac {rx + ay} {r ^ {2} + a ^ {2}} },{\frac {ry-ax}{r^{2}+a^{2}}},{\frac {z}{r}}\right)}$

( 12 )

${\displaystyle k_{0}=1.\!}$

( 13 )

Zauważ, że k jest wektorem jednostkowym . Tutaj M jest stałą masą wirującego obiektu, η jest tensorem Minkowskiego , a a jest stałym parametrem obrotowym wirującego obiektu. Zrozumiałe jest, że wektor jest skierowany wzdłuż dodatniej osi z. Wielkość r nie jest promieniem, lecz jest domyślnie zdefiniowana przez ${\displaystyle {\vec {a}}}$

${\ Displaystyle {\ Frac {x ^ {2} + Y ^ {2}} {r ^ {2} + A ^ {2}}} + {\ Frac {Z ^ {2}} {R ^ {2} }}=1}$

( 14 )

Zauważ, że ilość r staje się zwykłym promieniem R

${\ Displaystyle r \ do R = {\ sqrt {x ^ {2} + Y ^ {2} + z ^ {2}}}}$

gdy parametr rotacyjny a zbliża się do zera. W tej formie rozwiązania jednostki dobiera się tak, aby prędkość światła była jednością ( c = 1). Przy dużych odległościach od źródła ( R » ), równania te zredukować do postaci Eddington-Finkelsteina z Metryka Schwarzschilda .

W postaci Kerra-Schilda metryki Kerra wyznacznik tensora metryki jest wszędzie równy wartości ujemnej, nawet w pobliżu źródła.

Współrzędne solitonowe

Ponieważ metryka Kerra (wraz z metryką Kerra-NUT ) jest osiowo symetryczna, może być odlana do postaci, do której można zastosować transformację Belinskiego-Zakharova . Oznacza to, że czarna dziura Kerra ma postać grawitacyjnego solitonu .

Masa energii obrotowej

Jeśli wyekstrahowana zostanie cała energia obrotowa czarnej dziury, na przykład w procesie Penrose'a , pozostała masa nie może skurczyć się poniżej masy nieredukowalnej. Dlatego też, jeśli czarna dziura obraca się wraz ze spinem , jej całkowity równoważnik masowy jest wyższy o współczynnik w porównaniu z odpowiednią czarną dziurą Schwarzschilda, gdzie jest równy . Powodem tego jest to, że aby wprawić w ruch statyczne ciało, do systemu musi zostać dostarczona energia. Ze względu na równoważność masy i energii energia ta ma również równoważnik masy, który dodaje się do całkowitej masy i energii układu, . ${\ Displaystyle E_ {\ rm {rot}} = c ^ {2} \ lewo (M-M_ {\ rm {irr}} \ po prawej)}$${\displaystyle a=M}$${\ Displaystyle M}$${\displaystyle {\sqrt {2}}}$${\ Displaystyle M}$${\displaystyle M_{\rm {irr}}}$${\ Displaystyle M}$

Całkowity równoważnik masy (masa grawitacyjna) ciała (w tym jego energia obrotowa ) i jego masa nieredukowalna są powiązane wzorem ${\ Displaystyle M}$${\displaystyle M_{\rm {irr}}}$

${\ Displaystyle 2M_ {\ rm {irr}} ^ {2} = M ^ {2} + {\ sqrt {M ^ {4}-J ^ {2} c ^ {2} / G ^ {2}}} \Longrightarrow M^{2}={\frac {4M_{\rm {irr}}^{4}}{4M_{\rm {irr}}^{2}-a^{2}c^{4}/ G^{2}}}.}$

Operator fal

Ponieważ nawet bezpośrednie sprawdzenie na Kerr metryki obejmuje uciążliwych obliczeń, kontrawariantny elementy z tensora metrycznego we współrzędnych Boyer-Lindquist są przedstawione poniżej w wypowiedzi dla kwadratu cztery gradientu operatora : ${\ Displaystyle g ^ {ik}}$

${\ Displaystyle g ^ {\ mu \ nu} {\ Frac {\ częściowy} {\ częściowy x ^ {\ mu}}} {\ Frac {\ częściowy} {\ częściowy x ^ {\ nu}}} = - { \frac {1}{c^{2}\Delta }}\left(r^{2}+a^{2}+{\frac {r_{s}ra^{2}}{\Sigma }}\ sin ^{2}\theta \right)\left({\frac {\partial }{\partial t}}\right)^{2}-{\frac {2r_{s}ra}{c\Sigma \Delta }}{\frac {\częściowy }{\częściowy \phi }}{\frac {\częściowy }{\częściowy {t}}}+{\frac {1}{\Delta \sin ^{2}\theta } }\left(1-{\frac {r_{s}r}{\Sigma }}\right)\left({\frac {\partial }{\partial \phi }}\right)^{2}+{ \frac {\Delta }{\Sigma }}\left({\frac {\partial }{\częściowy r}}\right)^{2}+{\frac {1}{\Sigma }}\left({ \frac {\częściowy }{\częściowy \theta }}\prawo)^{2}}$

( 15 )

Przeciąganie ramek

Możemy przepisać metrykę Kerra ( 1 ) w następującej postaci:

${\ Displaystyle c ^ {2} d \ tau ^ {2} = \ lewo (g_ {tt} - {\ Frac {g_ {t \ phi} ^ {2}} {g_ {\ phi \ phi}}} \ po prawej)dt^{2}+g_{rr}dr^{2}+g_{\theta \theta }d\theta ^{2}+g_{\phi \phi }\lewo(d\phi +{\frac {g_{t\phi }}{g_{\phi \phi }}}dt\right)^{2}.}$

( 16 )

Ta metryka jest odpowiednikiem współobrotowego układu odniesienia, który obraca się z prędkością kątową Ω, która zależy zarówno od promienia r, jak i szerokości geograficznej θ , gdzie Ω nazywa się horyzontem zabijania .

${\ Displaystyle \ Omega = - {\ Frac {g_ {t \ phi}} {g_ {\ phi \ phi}}} = {\ Frac {R_ {s} rac} {\ Sigma \ lewo (r ^ {2} +a^{2}\right)+r_{s}ra^{2}\sin ^{2}\theta }}.}$

( 17 )

W ten sposób bezwładnościowa rama odniesienia jest porywana przez obracającą się masę centralną, aby uczestniczyć w jej obrocie; nazywa się to przeciąganiem ramek i zostało przetestowane eksperymentalnie. Jakościowo, przeciąganie klatek może być postrzegane jako grawitacyjny analog indukcji elektromagnetycznej. „Łyżwiarka”, na orbicie nad równikiem i obracając się w spoczynku względem gwiazd, wyciąga ramiona. Ramię wyciągnięte w kierunku czarnej dziury zostanie skręcone w kierunku obrotowym. Ramię odciągnięte od czarnej dziury zostanie dokręcone przeciw obrotowi. Będzie zatem przyspieszona rotacyjnie, w sensie przeciwbieżnym do czarnej dziury. To przeciwieństwo tego, co dzieje się w codziennym doświadczeniu. Jeśli już obraca się z określoną prędkością, gdy wyciąga ramiona, efekty bezwładności i przeciągania klatek zostaną zbalansowane, a jej obrót nie ulegnie zmianie. Ze względu na zasadę równoważności efekty grawitacyjne są lokalnie nie do odróżnienia od efektów bezwładności, więc ta szybkość rotacji, przy której, gdy wyciąga ramiona, nic się nie dzieje, jest jej lokalnym odniesieniem dla braku rotacji. Ta ramka obraca się względem gwiazd stałych i przeciwnie względem czarnej dziury. Przydatną metaforą jest system przekładni planetarnej , w którym czarna dziura jest kołem słonecznym, łyżwiarz jest kołem planetarnym, a wszechświat zewnętrzny jest kołem pierścieniowym. Można to również zinterpretować za pomocą zasady Macha .

Ważne powierzchnie

Położenie horyzontów, ergosfer i osobliwości pierścienia czasoprzestrzeni Kerra we współrzędnych kartezjańskich Kerra-Schilda.

Porównanie cienia (czarny) i ważnych powierzchni (biały) czarnej dziury. Parametr wirowania a jest animowany od 0 do M , podczas gdy lewa strona czarnej dziury obraca się w kierunku obserwatora.

Metryka Kerra ( 1 ) ma dwie fizycznie istotne powierzchnie, na których wydaje się być pojedyncza. Wewnętrzna powierzchnia odpowiada horyzontowi zdarzeń podobnemu do obserwowanego w metryce Schwarzschilda ; dzieje się tak, gdy czysto promieniowa składowa g _rr metryki zmierza do nieskończoności. Rozwiązanie równania kwadratowego 1 ⁄ g _rr  = 0 daje rozwiązanie:

${\ Displaystyle R_ {\ rm {H}} ^ {\ pm} = {\ Frac {r_ {s} \ pm {\ sqrt {r_ {s} ^ {2}-4a ^ {2}}}} {2 }}}$

co w jednostkach naturalnych (które dają G  =  M  =  c  = 1) upraszcza się do:

${\ Displaystyle R_ {\ Rm {H}} ^ {\ pm} = 1 \ pm {\ sqrt {1-a ^ {2}}}}$

Inna widoczna osobliwość występuje, gdy czysto czasowy składnik g _tt metryki zmienia się z dodatniego na ujemny. Ponownie rozwiązanie równania kwadratowego g _tt  = 0 daje rozwiązanie:

${\ Displaystyle R_ {\ rm {e}} ^ {\ pm} = {\ Frac {r_ {s} \ pm {\ sqrt {r_ {s} ^ {2}-4a ^ {2} \ cos ^ {2 }\theta }}}{2}}}$

lub w jednostkach naturalnych:

${\ Displaystyle R_ {\ rm {e}} ^ {\ pm } = 1 \ pm {\ sqrt {1-a ^ {2} \ cos ^ {2} \ teta}}}$

Ze względu na wyraz cos ² θ wyrażony w pierwiastku kwadratowym, ta zewnętrzna powierzchnia przypomina spłaszczoną kulę, która dotyka wewnętrznej powierzchni na biegunach osi obrotu, gdzie szerokość geograficzna θ jest równa 0 lub π ; przestrzeń pomiędzy tymi dwiema powierzchniami nazywana jest ergosferą . W obrębie tej objętości składowa czysto czasowa g _tt jest ujemna, tj. działa jak czysto przestrzenna składowa metryczna. W konsekwencji cząstki w tej ergosferze muszą współrotować z masą wewnętrzną, jeśli mają zachować swój czasopodobny charakter. Poruszająca się cząstka doświadcza pozytywnego właściwego czasu wzdłuż swojej linii świata , swojej ścieżki w czasoprzestrzeni . Jest to jednak niemożliwe w ergosferze, gdzie g _tt jest ujemne, chyba że cząstka obraca się z masą wewnętrzną M z prędkością kątową co najmniej Ω . W ten sposób żadna cząstka nie może obracać się przeciwnie do masy centralnej w ergosferze.

Jak z horyzontem zdarzeń w Schwarzschilda metryki pozorny osobliwości w r _H i r _E są złudzenia utworzone przez wybór współrzędnych (to znaczy, są współrzędnych osobliwości ). W rzeczywistości czasoprzestrzeń może być przez nie płynnie kontynuowana dzięki odpowiedniemu doborowi współrzędnych.

Ergosfera i proces Penrose'a

Ogólnie rzecz biorąc, czarna dziura jest otoczona przez powierzchnię, zwaną horyzontem zdarzeń i usytuowaną w promieniu Schwarzschilda dla nierotującej czarnej dziury, gdzie prędkość ucieczki jest równa prędkości światła. Na tej powierzchni żaden obserwator/cząstka nie może utrzymać się w stałym promieniu. Jest zmuszona opadać do wewnątrz, dlatego czasami nazywa się to granicą statyczną .

Obracająca się czarna dziura ma taką samą granicę statyczną w swoim horyzoncie zdarzeń, ale poza horyzontem zdarzeń istnieje dodatkowa powierzchnia zwana „ergopowierzchnią” podaną przez

${\ Displaystyle (RM) ^ {2} = M ^ {2} - J ^ {2} \ cos ^ {2} \ theta}$

we współrzędnych Boyera-Lindquista , które można intuicyjnie scharakteryzować jako sferę, w której „prędkość obrotowa otaczającej przestrzeni” jest przeciągana wraz z prędkością światła. W tej sferze przeciąganie jest większe niż prędkość światła i każdy obserwator/cząstka jest zmuszona do współobrotu.

Obszar poza horyzontem zdarzeń, ale wewnątrz powierzchni, w którym prędkość obrotowa jest prędkością światła, nazywany jest ergosferą (z greckiego ergon oznacza pracę ). Cząsteczki opadające w ergosferze są zmuszone do szybszego wirowania, a tym samym zyskują energię. Ponieważ wciąż znajdują się poza horyzontem zdarzeń, mogą uciec z czarnej dziury. Proces netto polega na tym, że obracająca się czarna dziura emituje energetyczne cząstki kosztem własnej całkowitej energii. Możliwość wydobycia energii spinowej z obracającej się czarnej dziury została po raz pierwszy zaproponowana przez matematyka Rogera Penrose'a w 1969 roku i dlatego jest nazywana procesem Penrose'a . Obracające się czarne dziury w astrofizyce są potencjalnym źródłem dużych ilości energii i są wykorzystywane do wyjaśniania zjawisk energetycznych, takich jak rozbłyski gamma .

Cechy geometrii Kerra

The Kerr geometria wykazuje wiele istotnych elementów: maksymalne rozszerzenie analityczny zawiera sekwencję asymptotycznie płaskich obszarach zewnętrznych, z których każdy skojarzony z ergoobszar , stacjonarne powierzchnie ograniczające, horyzontów zdarzeń , horyzontów Cauchy'ego , zamknięte krzywe czasopodobne oraz pierścieniowej krzywizny osobliwości . Geodezyjnej równanie może być rozwiązywane dokładnie w zamkniętej formie. Oprócz dwóch pól wektorów zabijania (odpowiadających translacji w czasie i symetrii osiowej ), geometria Kerra zawiera niezwykły tensor zabijania . Istnieje para głównych kongruencji zerowych (jedna przychodząca i jedna wychodząca ). Weyl tensor jest algebraicznie specjalny , w rzeczywistości ma typ Petrov D . Globalna struktura jest znana. Topologicznie typ homotopii czasoprzestrzeni Kerra można po prostu scharakteryzować jako linię z kółkami dołączonymi w każdym punkcie całkowitym.

Zauważ, że wewnętrzna geometria Kerra jest niestabilna w odniesieniu do zaburzeń w obszarze wewnętrznym. Ta niestabilność oznacza, że ​​chociaż metryka Kerra jest symetryczna względem osi, czarna dziura utworzona w wyniku kolapsu grawitacyjnego może tak nie być. Ta niestabilność oznacza również, że wiele cech geometrii Kerra opisanych powyżej może nie występować w takiej czarnej dziurze.

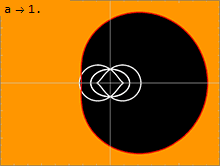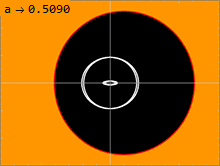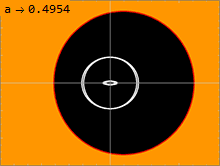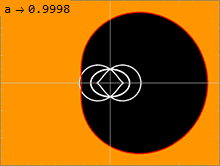
Powierzchnia, na której światło może krążyć wokół czarnej dziury, nazywana jest sferą fotonową. Rozwiązanie Kerra ma nieskończenie wiele sfer fotonowych leżących pomiędzy wewnętrzną a zewnętrzną. W nierotacyjnym rozwiązaniu Schwarzschilda, przy a = 0, wewnętrzna i zewnętrzna sfera fotonowa ulegają degeneracji, tak że w jednym promieniu jest tylko jedna sfera fotonowa. Im większy spin czarnej dziury, tym dalej od siebie oddalają się wewnętrzna i zewnętrzna sfera fotonowa. Wiązka światła podróżująca w kierunku przeciwnym do spinu czarnej dziury będzie okrążać dziurę w zewnętrznej sferze fotonowej. Wiązka światła podróżująca w tym samym kierunku, co spin czarnej dziury, będzie krążyć po okręgu wokół wewnętrznej sfery fotonowej. Orbitujące geodezy z pewnym momentem pędu prostopadłym do osi obrotu czarnej dziury będą krążyć po sferach fotonowych pomiędzy tymi dwoma ekstremami. Ponieważ czasoprzestrzeń się obraca, takie orbity wykazują precesję, ponieważ następuje przesunięcie zmiennej po zakończeniu jednego okresu w zmiennej. ${\displaystyle \phi \,}$${\displaystyle \theta\,}$

Równania trajektorii

Animacja orbity testowanej cząstki wokół wirującej czarnej dziury. Po lewej: widok z góry, po prawej: widok z boku.

Kolejna trajektoria masy testowej wokół wirującej (Kerr) czarnej dziury. W przeciwieństwie do orbit wokół czarnej dziury Schwarzschilda, orbita nie jest ograniczona do jednej płaszczyzny, ale ergodycznie wypełnia obszar podobny do torusa wokół równika.

Do równania ruchu dla cząsteczek testowych w czasoprzestrzeni Kerr są regulowane przez cztery stałe ruchu . Pierwsza to niezmienna masa badanej cząstki, określona zależnością ${\ Displaystyle \ mu}$

${\ Displaystyle - \ mu ^ {2} = p ^ {\ alfa} g_ {\ alfa \ beta} p ^ {\ beta}}$

gdzie jest czteropęd cząstki. Ponadto istnieją dwie stałe ruchu wynikające z symetrii przesunięcia w czasie i rotacji czasoprzestrzeni Kerra, energii i składowej orbitalnego momentu pędu równoległego do spinu czarnej dziury . ${\ Displaystyle p ^ {\ alfa}}$${\ Displaystyle E}$${\displaystyle L_{z}}$

${\ Displaystyle E = -p_ {t}}$, oraz

${\ Displaystyle L_ {z} = p_ {\ phi}}$

Korzystając z teorii Hamiltona-Jacobiego , Brandon Carter wykazał, że istnieje czwarta stała ruchu , obecnie nazywana stałą Cartera . Jest ona związana z całkowitym momentem pędu cząstki i jest wyrażona wzorem ${\displaystyle Q}$

${\ Displaystyle Q = p_ {\ theta} ^ {2} + \ cos ^ {2} \ theta \ lewo (a ^ {2} \ lewo (\ mu ^ {2} - E ^ {2} \ prawej) + \left({\frac {L_{z}}{\sin \theta }}\right)^{2}\right)}$.

Ponieważ istnieją cztery (niezależne) stałe ruchu dla stopni swobody, równania ruchu badanej cząstki w czasoprzestrzeni Kerra są całkowalne .

Korzystając z tych stałych ruchu, można zapisać równania trajektorii dla badanej cząstki (przy użyciu naturalnych jednostek G = M = c = 1),

${\ Displaystyle {\ zacząć {wyrównany} \ Sigma {\ Frac {dr}{d \ lambda}} i = \ pm {\ sqrt {R (r)}} \ \ \ Sigma {\ Frac {d \ theta} { d\lambda }}&=\pm {\sqrt {\Theta (\theta )}}\\\Sigma {\frac {d\phi }{d\lambda }}&=-\left(aE-{\frac {L_{z}}{\sin ^{2}\theta }}\right)+{\frac {a}{\Delta }}P(r)\\\Sigma {\frac {dt}{d\lambda }}&=-a\left(aE\sin ^{2}\theta -L_{z}\right)+{\frac {r^{2}+a^{2}}{\Delta }}P( r)\end{wyrównany}}}$

z

${\ Displaystyle \ Theta (\ theta) = Q-\ cos ^ {2} \ theta \ lewo (a ^ {2} \ lewo (\ mu ^ {2} - E ^ {2} \ prawej) + {\ Frac {L_{z}^{2}}{\sin ^{2}\theta }}\right)}$

${\ Displaystyle P (R) = E \ lewo (R ^ {2} + A ^ {2} \ prawej) - AL_ {Z}}$

${\ Displaystyle R (r) = P (r) ^ {2} - \ Delta \ lewo (\ mu ^ {2} r ^ {2} + (L_ {z} -aE) ^ {2} + Q \ prawej )}$

Gdzie jest parametrem afinicznym takim, że . W szczególności, gdy parametr affine jest powiązany z właściwym czasem przez . ${\ Displaystyle \ lambda}$${\ Displaystyle {\ Frac {dx ^ {\ alfa}} {d \ lambda}} = p ^ {\ alfa}}$${\ Displaystyle \ mu > 0}$${\ Displaystyle \ lambda}$${\ Displaystyle \ tau}$${\ Displaystyle \ lambda = \ tau / \ mu}$

Ze względu na efekt przeciągania klatek , obserwator z zerowym pędem kątowym (ZAMO) współrotuje z prędkością kątową, która jest określona w odniesieniu do współrzędnej czasu księgowego . Lokalną prędkość badanej cząstki mierzy się względem sondy współbieżnej z . Grawitacyjna dylatacja czasu pomiędzy ZAMO przy stałym i stacjonarnym obserwatorze oddalonym od masy wynosi ${\ Displaystyle \ Omega}$${\displaystyle t}$${\displaystyle v}$${\ Displaystyle \ Omega}$${\ Displaystyle r}$

${\ Displaystyle {\ Frac {t} {\ tau}} = {\ sqrt {\ Frac {\ lewo (a ^ {2} + r ^ {2} \ po prawej) ^ {2}-a ^ {2} \ Delta \sin ^{2}\theta }{\Delta \ \Sigma }}}}$.

Symetrie

Grupa izometrii metryki Kerra jest podgrupą dziesięciowymiarowej grupy Poincarégo, która zajmuje dwuwymiarowe miejsce osobliwości. Zachowuje przesunięcia czasowe (jeden wymiar) i obroty wokół własnej osi obrotu (jeden wymiar). Ma więc dwa wymiary. Podobnie jak grupa Poincaré, ma cztery połączone elementy: składnik tożsamości; element, który odwraca czas i długość geograficzną; składnik, który odbija się w płaszczyźnie równikowej; i komponent, który wykonuje obie te funkcje.

W fizyce symetrie są zazwyczaj związane z zachowanymi stałymi ruchu, zgodnie z twierdzeniem Noether . Jak pokazano powyżej, równania geodezyjne mają cztery zachowane wielkości: jedna z nich pochodzi z definicji geodezji, a dwie wynikają z przesunięcia w czasie i symetrii obrotowej geometrii Kerra. Czwarta zachowana wielkość nie wynika z symetrii w standardowym sensie i jest powszechnie określana jako ukryta symetria.

Ekstremalne rozwiązania Kerra

Położenie horyzontu zdarzeń jest określone przez większy pierwiastek . Gdy (tj. ), nie ma (o wartościach rzeczywistych) rozwiązań tego równania i nie ma horyzontu zdarzeń. Bez żadnych horyzontów zdarzeń, które mogłyby ją ukryć przed resztą wszechświata, czarna dziura przestaje być czarną dziurą, a zamiast tego będzie nagą osobliwością . ${\ Displaystyle \ Delta = 0}$${\displaystyle r_{s}/2<a}$${\displaystyle GM^{2}<Jc}$

Czarne dziury Kerra jako tunele czasoprzestrzenne

Chociaż rozwiązanie Kerra wydaje się być osobliwe dla pierwiastków Δ = 0, to w rzeczywistości są to współrzędne osobliwe i przy odpowiednim doborze nowych współrzędnych rozwiązanie Kerra można płynnie rozszerzyć o wartości odpowiadające tym pierwiastkom. Większy z tych pierwiastków określa położenie horyzontu zdarzeń, a mniejszy położenie horyzontu Cauchy'ego. Krzywa (zorientowana na przyszłość, podobna do czasu) może zaczynać się na zewnątrz i przechodzić przez horyzont zdarzeń. Po przejściu przez horyzont zdarzeń współrzędna zachowuje się teraz jak współrzędna czasowa, więc musi się zmniejszać, aż krzywa przejdzie przez horyzont Cauchy'ego. ${\ Displaystyle r}$${\ Displaystyle r}$

Region poza horyzontem Cauchy'ego ma kilka zaskakujących cech. W współrzędnych ponownie zachowuje się jak przestrzenne współrzędnych i może zmieniać się swobodnie. Obszar wewnętrzny ma symetrię odbicia, dzięki czemu krzywa (zorientowana na przyszłość, podobna do czasu) może kontynuować ścieżką symetryczną, która biegnie przez drugi horyzont Cauchy'ego, przez drugi horyzont zdarzeń i na zewnątrz do nowego obszaru zewnętrznego, który jest izometryczny względem oryginalnego obszaru zewnętrznego rozwiązania Kerra. Krzywa może wtedy uciec do nieskończoności w nowym obszarze lub wejść w przyszły horyzont zdarzeń nowego obszaru zewnętrznego i powtórzyć proces. Ta druga strona zewnętrzna jest czasami uważana za inny wszechświat. Z drugiej strony, w rozwiązaniu Kerra osobliwość jest pierścieniem , a krzywa może przechodzić przez środek tego pierścienia. Obszar poza pozwala na zamknięte krzywe czasopodobne. Ponieważ trajektoria obserwatorów i cząstek w ogólnej teorii względności jest opisana krzywymi podobnymi do czasu, obserwatorzy w tym regionie mogą powrócić do swojej przeszłości. To wewnętrzne rozwiązanie prawdopodobnie nie będzie fizyczne i uważane za czysto matematyczny artefakt. ${\ Displaystyle r}$

Chociaż oczekuje się, że zewnętrzny obszar rozwiązania Kerra jest stabilny i że wszystkie obracające się czarne dziury ostatecznie zbliżą się do metryki Kerra, wewnętrzny obszar rozwiązania wydaje się być niestabilny, podobnie jak ołówek wyważony na jego czubku. Wiąże się to z ideą kosmicznej cenzury .

Stosunek do innych dokładnych rozwiązań

The Kerr geometria jest szczególnym przykładem nieruchomym osiowo symetryczny roztworu próżni do równania pola Einsteina . Rodziną wszystkich stacjonarnych osiowo symetrycznych rozwiązań próżniowych równania pola Einsteina są próżnie Ernsta .

Rozwiązanie Kerra jest również powiązane z różnymi rozwiązaniami bezpróżniowymi, które modelują czarne dziury. Na przykład elektropróżnia Kerra-Newmana modeluje (wirującą) czarną dziurę obdarzoną ładunkiem elektrycznym, podczas gdy pył zerowy Kerra-Vaidya modeluje (wirującą) dziurę z wpadającym promieniowaniem elektromagnetycznym.

Specjalny przypadek metryki Kerra daje metrykę Schwarzschilda , która modeluje nierotującą czarną dziurę, która jest statyczna i sferycznie symetryczna we współrzędnych Schwarzschilda . (W tym przypadku każdy moment Gerocha, ale masa znika.) ${\displaystyle a=0}$

Wnętrze geometrii Kerr, a raczej jego część, jest lokalnie izometrycznego w próżni Chandrasekhar-Ferrari CPW , na przykład na fale zderzających płaszczyzny modelu. Jest to szczególnie interesujące, ponieważ globalna struktura tego rozwiązania CPW jest zupełnie inna niż geometria Kerra i w zasadzie eksperymentator mógłby mieć nadzieję na zbadanie geometrii (zewnętrznej części) wnętrza Kerra poprzez zorganizowanie kolizji dwie odpowiednie grawitacyjne fale płaskie .

Momenty wielobiegunowe

Każdą asymptotycznie płaską próżnię Ernsta można scharakteryzować podając nieskończoną sekwencję relatywistycznych momentów multipolowych , z których pierwsze dwa można interpretować jako masę i moment pędu źródła pola. Istnieją alternatywne sformułowania relatywistycznych momentów multipolowych autorstwa Hansena, Thorne'a i Gerocha, które okazują się ze sobą zgodne. Relatywistyczne momenty wielobiegunowe geometrii Kerra zostały obliczone przez Hansena; okazują się być

${\ Displaystyle M_ {n} = M [ia] ^ {n}}$

Tak więc szczególny przypadek próżni Schwarzschilda ( a  = 0) daje „ punktowe źródło monopolu ” ogólnej teorii względności.

Momenty multipolowe Weyla wynikają z potraktowania pewnej funkcji metrycznej (formalnie odpowiadającej newtonowskiemu potencjałowi grawitacyjnemu), która pojawia się na wykresie Weyla-Papapetrou dla rodziny Ernsta wszystkich stacjonarnych osiowosymetrycznych rozwiązań próżniowych przy użyciu standardowych euklidesowych skalarnych momentów multipolowych . Różnią się one od momentów wyliczonych przez Hansena powyżej. W pewnym sensie momenty Weyla tylko (pośrednio) charakteryzują „rozkład masy” izolowanego źródła i okazują się, że zależą one tylko od momentów relatywistycznych parzystego rzędu . W przypadku rozwiązań symetrycznych w poprzek płaszczyzny równikowej , momenty Weyla rzędu nieparzystego zanikają. W przypadku rozwiązań próżniowych Kerra, kilka pierwszych momentów Weyl jest podanych przez

${\ Displaystyle a_ {0} = M \ qquad a_ {1} = 0 \ qquad a_ {2} = M \ lewo ({\ Frac {M ^ {2}} {3}}-a ^ {2} \Prawidłowy)}$

W szczególności widzimy, że próżnia Schwarzschilda ma niezerowy moment Weyla drugiego rzędu, co odpowiada faktowi, że „monopol Weyla” jest rozwiązaniem próżni Chazy-Curzona , a nie rozwiązaniem próżni Schwarzschilda, które wynika z newtonowskiego potencjału pewnej skończonej długość jednolitej gęstości cienki pręt .

W ogólnej teorii względności pola słabego dogodnie jest traktować izolowane źródła przy użyciu innego typu multipola, który uogólnia momenty Weyla na masowe momenty multipolowe i momenty multipolowe pędu , charakteryzujące odpowiednio rozkład masy i pędu źródła. Są to wielkości o wielu indeksach, których odpowiednio symetryczne i antysymetryzowane części mogą być powiązane z rzeczywistymi i urojonymi częściami momentów relatywistycznych dla pełnej teorii nieliniowej w dość skomplikowany sposób.

Perez i Moreschi podali alternatywne pojęcie „rozwiązań monopolowych”, rozszerzając standardową tetradę NP próżni Ernsta o potęgi r (współrzędna radialna na wykresie Weyla-Papapetrou). Zgodnie z tym sformułowaniem:

• izolowane źródło monopolu masy o zerowym momencie pędu to rodzina próżni Schwarzschilda (jeden parametr),
• izolowanym źródłem monopolu masy z promieniowym momentem pędu jest rodzina próżni Taub-NUT (dwa parametry; nie całkiem asymptotycznie płaska),
• izolowanym monopolowym źródłem masy z osiowym momentem pędu jest rodzina próżni Kerra (dwa parametry).

W tym sensie próżni Kerra są najprostszymi stacjonarnymi osiowosymetrycznymi asymptotycznie płaskimi rozwiązaniami próżni w ogólnej teorii względności.

Otwarte problemy

Geometria Kerra jest często używana jako model wirującej czarnej dziury . Ale jeśli uznamy, że rozwiązanie jest ważne tylko poza jakimś zwartym obszarem (z pewnymi ograniczeniami), w zasadzie powinniśmy być w stanie użyć go jako zewnętrznego rozwiązania do modelowania pola grawitacyjnego wokół wirującego, masywnego obiektu innego niż czarna dziura, takich jak gwiazda neutronowa lub Ziemia. Działa to bardzo dobrze w przypadku nieobrotowego, gdzie możemy dopasować zewnętrzną próżnię Schwarzschilda do wnętrza płynu Schwarzschilda , a także do bardziej ogólnych, statycznych, sferycznie symetrycznych doskonałych rozwiązań płynów . Jednak problem ze znalezieniem wirującego wnętrza o doskonałym płynie, które można dopasować do zewnętrznej powierzchni Kerra, lub w rzeczywistości do dowolnego asymptotycznie płaskiego rozwiązania zewnętrznego podciśnienia, okazał się bardzo trudny. W szczególności płyn Wahlquista , który kiedyś uważano za kandydata do dopasowania do zewnętrznej powierzchni Kerra, obecnie nie dopuszcza takiego dopasowania. Obecnie wydaje się, że znane są tylko przybliżone rozwiązania modelujące wolno obracające się kule płynów. (Są to relatywistyczny odpowiednik spłaszczonych (grubych, przysadzistych) kulek o niezerowej masie i momencie pędu, ale zanikających wyższych momentów multipolowych.) Jednak zewnętrzna strona dysku Neugebauera-Meinela , dokładne rozwiązanie pyłu, które modeluje obracający się cienki dysk, zbliża się w granicznym przypadku do geometrii Kerra. Znane są również fizyczne rozwiązania cienkich dysków uzyskane przez identyfikację części czasoprzestrzeni Kerra. ${\ Displaystyle GM ^ {2} = cJ}$

Zobacz też

• Metryka Schwarzschilda
• Metryka Kerra-Newmana
• metryka Reissner-Nordström
• Spin-flip
• Czasoprzestrzeń Kerra-Schilda
• Obracająca się czarna dziura

Przypisy

Bibliografia

Dalsza lektura

• Wiltshire, David L.; Visser, Matt; Scott, Susan M. , wyd. (2009). Czasoprzestrzeń Kerra: rotacja czarnych dziur w ogólnej teorii względności . Cambridge: Wydawnictwo Uniwersytetu Cambridge. Numer ISBN 978-0-521-88512-6.
• Stefani, Hans; Kramer, Dietrich; MacCallum, Malcolm; Hoenselaers, Korneliusz; Herlt, Edward (2003). Dokładne rozwiązania równań pola Einsteina . Cambridge: Wydawnictwo Uniwersytetu Cambridge. Numer ISBN 978-0-521-46136-8.
• Meinel, Reinhard ; Ansorg, Marcus; Kleinwachter, Andreas; Neugebauera, Gernota; Petroff, Dawid (2008). Relatywistyczne figury równowagi . Cambridge: Wydawnictwo Uniwersytetu Cambridge. Numer ISBN 978-0-521-86383-4.
• O'Neill, Barrett (1995). Geometria czarnych dziur Kerra . Wellesley, Massachusetts: AK Peters. Numer ISBN 978-1-56881-019-5.
• D'Inverno, Ray (1992). Przedstawiamy teorię względności Einsteina . Oxford: Clarendon Press. Numer ISBN 978-0-19-859686-8. Zobacz rozdział 19, aby zapoznać się z czytelnym wprowadzeniem na zaawansowanym poziomie licencjackim.
• Chandrasekhar, S. (1992). Matematyczna teoria czarnych dziur . Oxford: Clarendon Press. Numer ISBN 978-0-19-850370-5. Zobacz rozdziały 6-10, aby zapoznać się z bardzo dokładnym studium na poziomie zaawansowanym.
• Griffiths, JB (1991). Zderzające się fale płaskie w ogólnej teorii względności . Oksford: Oxford University Press. Numer ISBN 978-0-19-853209-5. Patrz rozdział 13 dla modelu Chandrasekhar/Ferrari CPW.
• Adlera, Ronalda; Bazin, Maurycy; Schiffer, Menahem (1975). Wprowadzenie do ogólnej teorii względności (druga red.). Nowy Jork: McGraw-Hill. Numer ISBN 978-0-07-000423-8. Patrz rozdział 7 .
• Penrose, R. (1968). red. C. de Witt i J. Wheeler (red.). Battelle Rencontres . WA Benjamin, Nowy Jork. P. 222.
• Perez, Alejandro; Moreschi, Osvaldo M. (2000). „Charakteryzowanie dokładnych rozwiązań z asymptotycznych pojęć fizycznych”. arXiv : gr-qc/0012100v1 . Charakterystyka trzech standardowych rodzin rozwiązań próżniowych, jak wspomniano powyżej.
• Sotiriou, Thomas P.; Apostolatos, Theocharis A. (2004). „Korekty i komentarze dotyczące momentów wielobiegunowych osiowosymetrycznych czasoprzestrzeni elektropróżniowych”. Klasa. Grawitacja kwantowa . 21 (24): 5727–5733. arXiv : gr-qc/0407064 . Kod Bib : 2004CQGra..21.5727S . doi : 10.1088/0264-9381/21/24/003 . S2CID  16858122 . Podaje relatywistyczne momenty multipolowe dla próżni Ernsta (plus elektromagnetyczne i grawitacyjne relatywistyczne momenty multipolowe dla naładowanego uogólnienia).
• Carter, B. (1971). „Osisymetryczna czarna dziura ma tylko dwa stopnie swobody”. Fizyczne listy kontrolne . 26 (6): 331-333. Kod bib : 1971PhRvL..26..331C . doi : 10.1103/PhysRevLett.26.331 .
• Wald, RM (1984). Ogólna teoria względności . Chicago: Wydawnictwo Uniwersytetu Chicago. s. 312–324. Numer ISBN 978-0-226-87032-8.
• Kerra, RP; Schild, A. (2009). „Republikacja: Nowa klasa próżniowych rozwiązań równań pola Einsteina”. Ogólna teoria względności i grawitacja . 41 (10): 2485-2499. Kod Bib : 2009GReGr..41.2485K . doi : 10.1007/s10714-009-0857-z . S2CID  361088 .
• Krasiński, Andrzej; Verdaguer, Enric; Kerr, Roy Patrick (2009). „Nota redakcyjna do: RP Kerr i A. Schild, Nowa klasa próżniowych rozwiązań równań pola Einsteina” . Ogólna teoria względności i grawitacja . 41 (10): 2469-2484. Kod bib : 2009GReGr..41.2469K . doi : 10.1007/s10714-009-0856-0 . „… Ta notatka ma być przewodnikiem dla tych czytelników, którzy chcą zweryfikować wszystkie szczegóły [wyprowadzenia rozwiązania Kerra]…”